K 凸函数的一些性质和相关证明

一、K 凸函数的定义：

定义1 $\quad\forall~ a, b>0$

K + f (a + x) - f (x) - a {\frac{f (x) - f (x - b)}{b}} \geq 0

$K+f(a+x)-f(x)-a\Big\{\frac{f(x)-f(x-b)}{b}\Big\}\geq 0$
定义2

\forall a > 0

$\quad\forall~ a>0$

K + f (a + x) - f (x) - a f^{'} (x) \geq 0

$K+f(a+x)-f(x)-af'(x)\geq 0$
定义3

\forall 0 < μ < 1

$\quad\forall~ 0<\mu<1$

μ f (x_{1}) + (1 - μ) (f (x_{2}) + K) \geq f (μ x_{1} + (1 - μ) x_{2})

$\mu f(x_1)+(1-\mu)(f(x_2)+K)\geq f(\mu x_1+(1-\mu)x_2)$

定义3 其实由定义1 改造而来，只要令 $x_1=x-b$ , $x_2=x+a$ , $\mu=\frac{a}{a+b}$ 即可。

二、一个 K 凸函数图像：

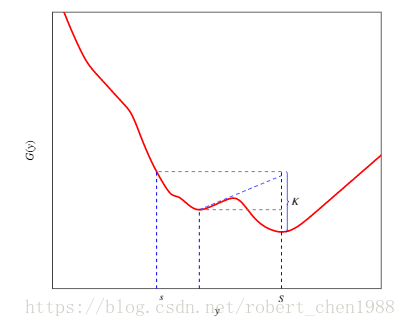
这里写图片描述

三、 $s$ , $S$ 的定义

设 $f$ 为在定义域 $[A, B]$ 上的一个 K 凸函数， $f^\ast$ 为其在定义域内的最小值，

\begin{aligned} S & = {x ∣ f (x) = f^{*}} \\ s & = min {x ∣ f (x) \leq f^{*} + K, x \leq B} \end{aligned}

$\begin{align} S&=\{x\mid f(x)=f^\ast\}\nonumber\\ s&=\min\{x\mid f(x)\leq f^\ast+K, x\leq B\}\nonumber \end{align}$
注：

s

$s$ 可能不在定义域内。

四、K-凸函数的相关性质

1. $f(x)$ 在区间 $[A, s]$ 上单调递减.

证明：当 $x<s$ 时，根据 $s$ 的定义，显然 $f(x)>f(S)+K$ 。令 $x+a=S$ ，则根据定义1 或定义 2，当 $x<s$ 时,

a f^{'} (x) \leq K + f (S) - f (x) < 0

$af'(x)\leq K+f(S)-f(x)<0$
因此

f (x)

$f(x)$ 在区间

[A, s]

$[A, s]$ 上单调递减。

2. 对任意 $s<x_1<x_2$ ，都有 $f(x_2)+K\geq f(x_1)$ .

证明：
(1) 若 $x_2>x_1\geq S$ 或 $x_1<x_2\leq S$ , 在定义1 中令 $x-b=S$ , $x+a=x_2$ , $x=x_1$ ，得到：

\begin{aligned} K + f (x_{2}) - f (x_{1}) - (x_{2} - x_{1}) {\frac{f (x_{1}) - f (S)}{x_{1} - S}} \geq 0 \\ \Rightarrow & K + f (x_{2}) - f (x_{1}) \geq (x_{2} - x_{1}) {\frac{f (x_{1}) - f (S)}{x_{1} - S}} \\ \Rightarrow & K + f (x_{2}) - f (x_{1}) \geq 0 (since f (x_{1}) \geq f (S)) \end{aligned}

$\begin{align} &K+f(x_2)-f(x_1)-(x_2-x_1)\Big\{\frac{f(x_1)-f(S)}{x_1-S}\Big\}\geq 0\nonumber\\ \Rightarrow~~&K+f(x_2)-f(x_1)\geq (x_2-x_1)\Big\{\frac{f(x_1)-f(S)}{x_1-S}\Big\}\nonumber\\ \Rightarrow~~&K+f(x_2)-f(x_1)\geq 0\quad\big (\text{since}~~f(x_1)\geq f(S)\big )\nonumber \end{align}$
(2) 若

x_{1} < S < x_{2}

$x_1<S<x_2$ ，在定义1 中令

x + a = S

$x+a=S$ ,

x - b = s

$x-b=s$ ,

x = x_{1}

$x=x_1$ ，得到：

\begin{aligned} K + f (S) - f (x_{1}) - (S - x_{1}) {\frac{f (x_{1}) - f (s)}{x_{1} - s}} \geq 0 \\ \Rightarrow & K + f (S) - f (x_{1}) \geq (S - x_{1}) {\frac{f (x_{1}) - f (S) - K}{x_{1} - s}} \\ \Rightarrow & K + f (S) - f (x_{1}) \geq 0 \Rightarrow K + f (x_{2}) - f (x_{1}) \geq 0 (since f (x_{2}) \geq f (S)) \end{aligned}

$\begin{align} &K+f(S)-f(x_1)-(S-x_1)\Big\{\frac{f(x_1)-f(s)}{x_1-s}\Big\}\geq 0\nonumber\\ \Rightarrow~~&K+f(S)-f(x_1)\geq (S-x_1)\Big\{\frac{f(x_1)-f(S)-K}{x_1-s}\Big\}\nonumber\\ \Rightarrow~~&K+f(S)-f(x_1)\geq 0\quad\Rightarrow K+f(x_2)-f(x_1)\geq 0\quad\big (\text{since}~~f(x_2)\geq f(S)\big )\nonumber \end{align}$

3. 在定义域 $[A, B]$ 上的最优订货策略为 $(s, S)$ , 即：

\begin{aligned} g (x) = & inf_{y \geq x, A \leq y \leq B} [K δ (y - x) + f (y)] \\ = & {\begin{cases} f (S) + K & x < s \\ f (x) & x \geq s \end{cases} \end{aligned}

$\begin{align} g(x)=&\inf_{y\geq x, A\leq y\leq B} \big [K\delta (y-x)+f(y)\big ]\nonumber\\ \nonumber\\ =&\begin{cases} f(S)+K\quad &x<s\\ f(x)\quad &x\geq s \end{cases}\nonumber \end{align}$

需要证明当 $f(x)$ 为 k 凸函数时， $g(x)$ 为 k 凸函数。
证明：我们需证明 $g(x)$ 满足定义1. 对任意三个点 $x-b$ , $x$ , $x+a$
一共有以下四种情况：
(1) 若 $x-b\geq s$ 时，

\begin{aligned} K + g (x + a) - g (x) - a {\frac{g (x) - g (x - b)}{b}} \\ = & K + f (x + a) - f (x) - a {\frac{g (x) - g (x - b)}{b}} \end{aligned}

$\begin{align} &K+g(x+a)-g(x)-a\Big\{\frac{g(x)-g(x-b)}{b}\Big\}\nonumber\\ =&K+f(x+a)-f(x)-a\Big\{\frac{g(x)-g(x-b)}{b}\Big\}\nonumber \end{align}$
上式就是

f (x)

$f(x)$ K凸函数的定义，显然成立。

(2) 若 $x+a< s$ 时，

\begin{aligned} K + g (x + a) - g (x) - a {\frac{g (x) - g (x - b)}{b}} \\ = & K + f (S) + K - f (S) - K - a {\frac{f (S) + K - f (S) - K}{b}} \\ = & 0 \end{aligned}

$\begin{align} &K+g(x+a)-g(x)-a\Big\{\frac{g(x)-g(x-b)}{b}\Big\}\nonumber\\ =&K+f(S)+K-f(S)-K-a\Big\{\frac{f(S)+K-f(S)-K}{b}\Big\}\nonumber\\ =&0\nonumber \end{align}$
上式显然是 K凸函数。

(3) 若 $x-b<x<s<x+a$ 时，

\begin{aligned} K + g (x + a) - g (x) - a {\frac{g (x) - g (x - b)}{b}} \\ = & K + f (x + a) - f (S) - K - a {\frac{f (S) + K - f (S) - K}{b}} \\ = & f (x + a) - f (S) \geq 0 \end{aligned}

$\begin{align} &K+g(x+a)-g(x)-a\Big\{\frac{g(x)-g(x-b)}{b}\Big\}\nonumber\\ =&K+f(x+a)-f(S)-K-a\Big\{\frac{f(S)+K-f(S)-K}{b}\Big\}\nonumber\\ =&f(x+a)-f(S)\geq 0\nonumber \end{align}$
为 K凸函数。

(4) 若 $x-b<s<x$ 时，

\begin{aligned} K + g (x + a) - g (x) - a {\frac{g (x) - g (x - b)}{b}} \\ = & K + f (x + a) - f (x) - a {\frac{f (x) - f (S) - K}{b}} \\ \geq & K + f (x + a) - f (x) - a {\frac{f (x) - f (s)}{b}} \end{aligned}

$\begin{align} &K+g(x+a)-g(x)-a\Big\{\frac{g(x)-g(x-b)}{b}\Big\}\nonumber\\ =&K+f(x+a)-f(x)-a\Big\{\frac{f(x)-f(S)-K}{b}\Big\}\nonumber\\ \geq &K+f(x+a)-f(x)-a\Big\{\frac{f(x)-f(s)}{b}\Big\}\nonumber \end{align}$

根据性质2， $K+f(x+a)-f(x)\geq 0$ 。
若 $f(x)\leq f(s)$ ，上式显然大于等于零。
若 $f(x)< f(s)$ ，根据性质 1，可以得出 $x>s$ ，又因为 $x-b<s$ ，即 $b>x-s$ ，上述表达式可以变为：

\begin{aligned} K + f (x + a) - f (x) - a {\frac{f (x) - f (s)}{b}} \\ \geq & K + f (x + a) - f (x) - a {\frac{f (x) - f (s)}{x - s}} \end{aligned}

$\begin{align} &K+f(x+a)-f(x)-a\Big\{\frac{f(x)-f(s)}{b}\Big\}\nonumber\\ \geq &K+f(x+a)-f(x)-a\Big\{\frac{f(x)-f(s)}{x-s}\Big\}\nonumber \end{align}$

刚好为 K凸函数的定义，因此也大于等于零。

综合以上，在四种情况下， $g(x)$ 均为 K 凸函数。 $\Box$