文章目录
前言
课程作业:
某房地产开发公司拟在长江三角洲、珠江三角洲和环渤海地区中选择有投资价值潜力的目标城市进行投资
- 如何衡量投资潜力?
- 给出一些指标
请对备选城市进行综合评价,遴选出具有投资潜力的城市
一、数据描述
数据如下所示
| 城市 | GDP | 人均可支配收入 | 城市化水平 | 人均使用面积 | 户籍人口数量 | 商品房销售均价 | 商品房销售面积 | 商品房施工面积 | |
| 0 | 深圳 | 5684.39 | 22567 | 83.7 | 19.7 | 196.83 | 9230 | 784.63 | 3122.10 |
| 1 | 北京 | 9006.20 | 21989 | 84.3 | 20.1 | 1213.30 | 8792 | 2176.60 | 10438.60 |
| 2 | 杭州 | 3440.99 | 19027 | 62.1 | 21.0 | 666.31 | 7751 | 762.50 | 4545.33 |
| 3 | 上海 | 10296.97 | 20668 | 88.7 | 16.5 | 1368.10 | 7038 | 3025.40 | 10938.75 |
| 4 | 广州 | 6068.41 | 19851 | 69.5 | 19.4 | 760.72 | 6545 | 1316.88 | 5460.37 |
| 5 | 宁波 | 2864.50 | 19674 | 59.0 | 18.7 | 560.40 | 5437 | 601.10 | 2200.00 |
| 6 | 天津 | 4337.73 | 14283 | 75.7 | 26.1 | 948.88 | 5013 | 1458.60 | 4271.14 |
| 7 | 南京 | 2774.00 | 17538 | 62.1 | 20.4 | 607.23 | 5002 | 932.40 | 3264.44 |
| 8 | 苏州 | 4820.26 | 14451 | 62.1 | 20.4 | 615.55 | 4958 | 932.40 | 5058.09 |
| 9 | 大连 | 2569.70 | 13350 | 57.5 | 17.5 | 572.10 | 4844 | 628.80 | 2196.10 |
| 10 | 珠海 | 749.60 | 17671 | 59.4 | 25.0 | 92.63 | 4731 | 178.88 | 678.55 |
| 11 | 台州 | 1467.48 | 19036 | 57.2 | 32.8 | 564.66 | 4726 | 259.72 | 1238.32 |
| 12 | 绍兴 | 1678.19 | 19486 | 57.2 | 25.4 | 435.50 | 4500 | 366.00 | 1355.36 |
| 13 | 常州 | 1560.00 | 16649 | 62.1 | 28.4 | 354.70 | 4500 | 479.40 | 1701.90 |
| 14 | 南通 | 1758.34 | 14058 | 62.1 | 29.4 | 769.79 | 4500 | 473.27 | 1165.86 |
| 15 | 无锡 | 3300.00 | 18189 | 70.0 | 31.3 | 457.80 | 4315 | 626.00 | 2322.17 |
| 16 | 嘉兴 | 1340.00 | 17828 | 52.0 | 32.1 | 335.50 | 4299 | 359.50 | 1393.70 |
| 17 | 舟山 | 333.20 | 17525 | 52.0 | 22.2 | 96.58 | 4299 | 91.80 | 300.00 |
| 18 | 东莞 | 2624.63 | 25320 | 65.0 | 45.2 | 168.31 | 4192 | 379.43 | 1431.27 |
| 19 | 湖州 | 760.89 | 17503 | 53.0 | 27.0 | 257.89 | 4134 | 195.19 | 887.51 |
可以看到有很多变量是与经济指标相关的,就意味着这些变量有可能是高度相关的,接下来就是对变量进行描述性统计。
二、变量描述性统计
1.单变量直方图
代码如下:
import pandas as pd
import matplotlib.pyplot as plt # 导入包
data=pd.read_excel('城市投资潜力.xlsx') # 读入数据
plt.rcParams['font.sans-serif']=['simhei'] # 添加中文字体为黑体
plt.rcParams['axes.unicode_minus'] =False
def draw(data):
data.hist(figsize=(16,14))
#plt.savefig("Plots.jpg",dpi=300, pad_inches = 0)
plt.title('各变量的频数分布图')
plt.show()
draw(data.iloc[:,1:])
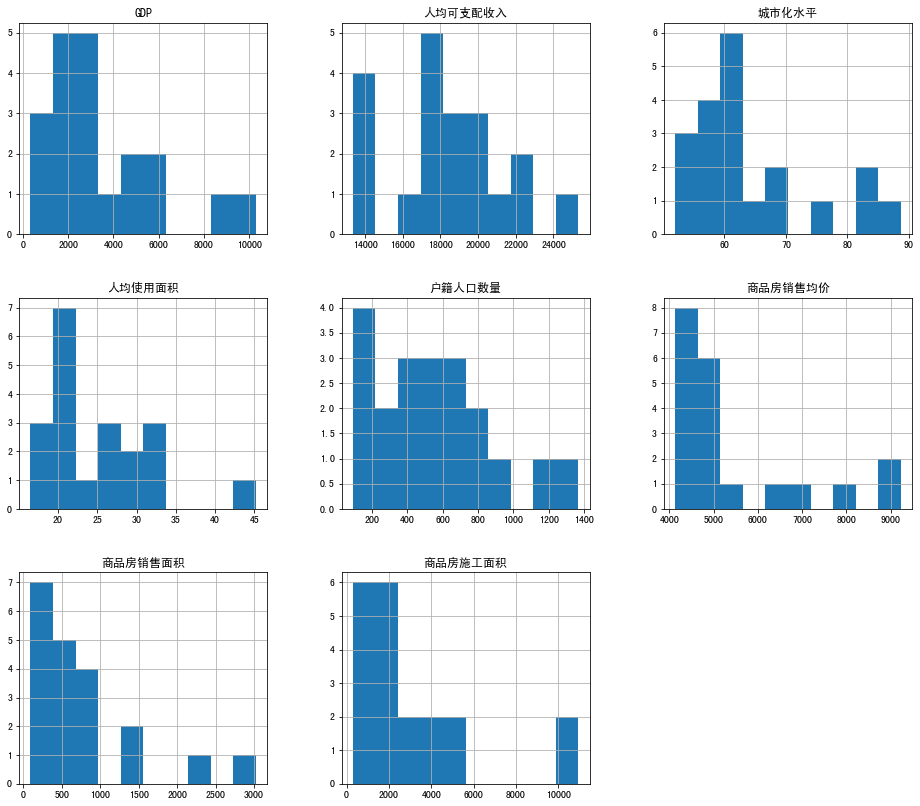
可以看到,大部变量都是右偏,分布较不规律,但可能因为样本个数较少导致的。
2.相关系数图
代码如下:
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
data1=data.iloc[:,1:] #定义数值型变量
import numpy as np
print(np.var(data1))
fig, ax = plt.subplots(figsize = (9,9))
corr = data1.corr()
sns.heatmap(corr, vmax=1,vmin = 0,
xticklabels= True, yticklabels= True, square=True, cmap="YlGnBu")

可以看到有的变量之间的相关系数较高,如商品房销售面积和商品房施工面积,户籍人口数量和商品房销售面积、商品房施工面积等,所以后续考虑对这些变量进行筛选
3.散点图矩阵
代码如下:
import mglearn
import matplotlib.pyplot as plt
grr = pd.plotting.scatter_matrix(data.iloc[:,1:],figsize=(15,15),marker='o',hist_kwds={
'bins':20},cmap=mglearn.cm3)
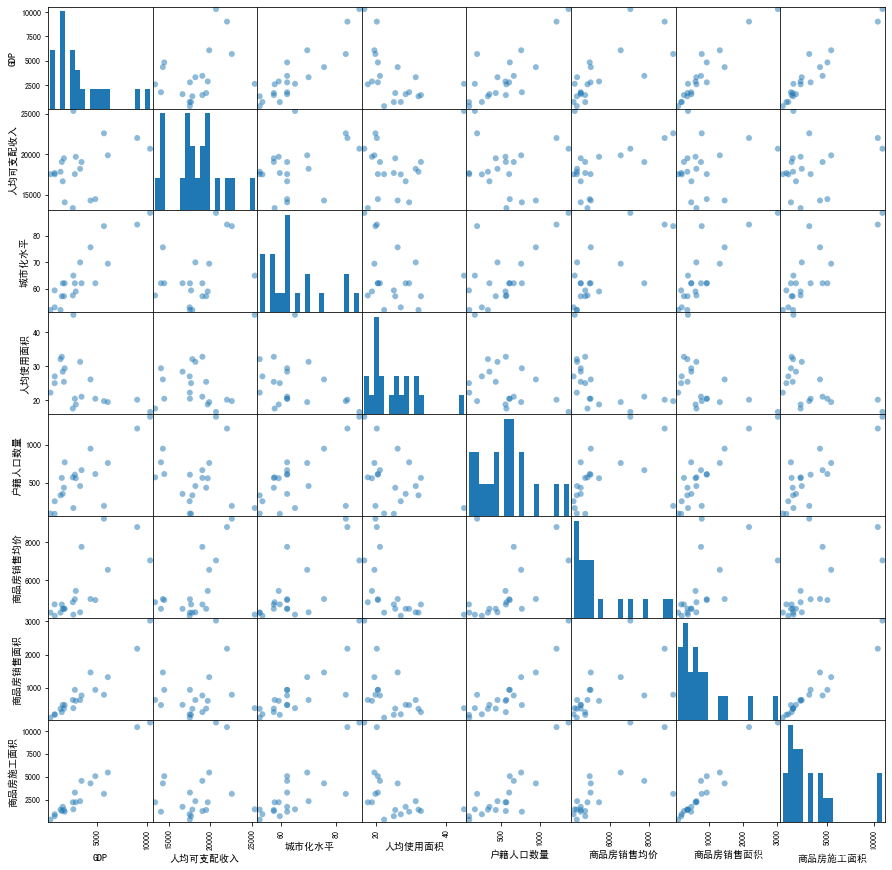
从散点图矩阵中可以看出
- GDP与商品房施工面积、商品房销售面积、城市化水平等变量相关性比较高
- 商品房销售面积和商品房施工面积相关性较高
所以对数据进行主成分分析、因子分析有一定依据
三、城市房地产投资潜力分析
1.变量选择及逆指标的变换
(1)指标选取
参考 https://www.sohu.com/a/423745747_796547 选取指标
投资潜力指标:
- 经济发展情况(GDP):正向指标,衡量地区经济发展状况。
- 人口规模(户籍人口数量):正向指标,衡量地区房地产潜在的总需求。
- 需求规模(商品房销售面积):正向指标,衡量报告期内房地产市场的需求。
- 购买力水平 (人均可支配收入):正向指标,衡量房地产市场的购买力
- 城市化水平:正向指标,衡量城市发展状况及经济水平。
- 商品房销售均价:正向指标衡量
- 人均使用面积:负向指标,人均使用面积=住宅使用面积/居住人口,衡量了一个城市现有住宅,人均使用面积越小说明还有发展潜力.
- 供给规模(商品房施工面积):负向指标,施工面积反映了1~2年内的期房和现房供应量,衡量了竞争关系。
投资风险指标:
- 供求风险=施工面积/销售面积.负向指标,施工面积反映了1~2年内的期房和现房供应量;施工面积/销售面积比值的变化反映供求是否平衡发展,该指标的异常变化能对下一年度的价格走势起到一定预示性作用。
- 购买力风险=商品房销售均价/人均可支配收入,负向指标,衡量现在房价水平是否合理
由上分析可知,人均使用面积、商品房施工面积、供求风险、购买力风险为逆向指标,需要进行逆向化处理
2.指标变换方法
参考文献:《综合评价中指标标准化方法研究》李美娟
对负向指标进行转换及所有指标的归一化处理:(变量取值范围不变,且保留了变量的变异程度信息)
- 负向指标转换:
x i , j ′ = m a x 1 ≤ i ≤ n x i , j − x i , j + m i n 1 ≤ i ≤ n x i , j x^{'}_{i,j}=\mathop{max}\limits_{1 \leq i \leq n} x_{i,j} -x_{i,j}+\mathop{min}\limits_{1 \leq i \leq n} x_{i,j} xi,j′=1≤i≤nmaxxi,j−xi,j+1≤i≤nminxi,j - 所有变量归一化处理
y i , j = x i , j ∑ i = 1 n x i , j , ( 1 ≤ i ≤ n , 1 ≤ j ≤ m ) y_{i,j}=\frac{x_{i,j}}{\sum_{i=1}^{n}x_{i,j}},(1\leq i\leq n,1\leq j\leq m) yi,j=∑i=1nxi,jxi,j,(1≤i≤n,1≤j≤m) - 为避免由于样本个数n较多造成 y i , j y_{i,j} yi,j较小的情形,乘以n
y i , j ′ = y i , j × n , ( 1 ≤ i ≤ n , 1 ≤ j ≤ m ) y^{'}_{i,j}=y_{i,j} \times n,(1\leq i\leq n,1\leq j\leq m) yi,j′=yi,j×n,(1≤i≤n,1≤j≤m)
这种方法保留了以下优点:
-
(l)经标准化处理后的标准值较真实地反映原指标值之间的关系,考虑了指标值之间的差异性;
-
(2)正、逆向指标均化为正向指标,即均具有指标值越大越好的特性;
-
(3)不管决策矩阵 X X X中的指标值是正数还是负数,都适用,经过该标准化处理后,标准化指标值满足, 0 < y < m 0<y<m 0<y<m。
克服了以下缺点:
-
(l)忽略了决策矩阵 X X X中的指标值的差异性;
-
(2)要求任意 x > 0 x>0 x>0,如果存在 x ≤ 0 x\leq 0 x≤0则不适用;
-
(3)进行了非线性变换,变换后的指标值无法客观地反映原始指标间的相互关系。
-
(4)正、逆向指标的方向没有发生变化。即正向指标归一化变换后,仍是正向指标。逆向指标归一化变换后,也仍是逆向指标。该标准化方法保持了原始指标值间的相互关系。
#构造上述负向指标处理的函数
def convert(x):
re=[max(x)-i+min(x) for i in x]
return re
#构造上述归一化处理的函数
def rescale(x):
re=[i*len(x)/sum(x) for i in x]
return re
#指标归一化min-max
pos_var=['GDP', '人均可支配收入', '城市化水平', '户籍人口数量', '商品房销售均价','商品房销售面积']
neg_var=['人均使用面积','商品房施工面积','供求风险','购买力风险']
trans_data=data.copy()
trans_data['供求风险']=trans_data['商品房施工面积']/trans_data['商品房销售面积']
trans_data['购买力风险']=trans_data['商品房销售均价']/trans_data['人均可支配收入']
#负向指标转换
trans_data.loc[:,neg_var]=trans_data.loc[:,neg_var].apply(convert)
#保留正向、负向指标和城市名
trans_data=trans_data.loc[:,['城市']+pos_var+neg_var]
#归一化处理
trans_data.iloc[:,1:]=trans_data.iloc[:,1:].apply(rescale)
#归一化后的变量描述
trans_data.describe()
| GDP | 人均可支配收入 | 城市化水平 | 户籍人口数量 | 商品房销售均价 | 商品房销售面积 | 人均使用面积 | 商品房施工面积 | 供求风险 | 购买力风险 | |
|---|---|---|---|---|---|---|---|---|---|---|
| count | 20.000000 | 20.000000 | 20.000000 | 20.000000 | 20.000000 | 20.000000 | 20.000000 | 20.000000 | 20.000000 | 20.000000 |
| mean | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| std | 0.795272 | 0.164151 | 0.166660 | 0.624525 | 0.287475 | 0.905143 | 0.188521 | 0.368436 | 0.182380 | 0.245504 |
| min | 0.098820 | 0.728189 | 0.803275 | 0.167766 | 0.759885 | 0.114546 | 0.448735 | 0.037312 | 0.550274 | 0.599463 |
| 25% | 0.455805 | 0.943073 | 0.887078 | 0.572496 | 0.818659 | 0.454659 | 0.898831 | 0.858063 | 0.933263 | 0.830985 |
| 50% | 0.800562 | 0.982292 | 0.959296 | 1.018820 | 0.880007 | 0.765574 | 1.036171 | 1.124427 | 1.046228 | 1.063730 |
| 75% | 1.322260 | 1.075552 | 1.075539 | 1.249527 | 1.050310 | 1.163428 | 1.134077 | 1.232875 | 1.091579 | 1.195953 |
| max | 3.053873 | 1.381105 | 1.370202 | 2.477818 | 1.696598 | 3.775026 | 1.229263 | 1.360495 | 1.331579 | 1.480923 |
2.熵权法
- 目前有关房地产投资的分析中有关变量权重的主要使用的方法有:
- 专家打分法
- 熵权值法
因为第一种方法需要专家进行打分,且不同专家打分可能会导致不同的排序结果,目前没有针对各个变量权威的权重,而且这个方法有一定的主观性,这里考虑熵权法进行排序。
-
在信息论中,熵是对不确定性的一种度量。不确定性越大,熵就越大,包含的信息量越大;不确定性越小,熵就越小,包含的信息量就越小。
根据熵的特性,可以通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响(权重)越大。比如样本数据在某指标下取值都相等,则该指标对总体评价的影响为0,权值为0,熵权法是一种客观赋权法,因为它仅依赖于数据本身的离散性。 -
方法描述:对 n n n个样本, m m m个指标,则 x i , j x_{i,j} xi,j为第 i i i个样本的第 j j j个指标的数值( i = 1 , ⋯ , n , j = 1 , ⋯ , m i=1,\cdots,n,\ j=1,\cdots,m i=1,⋯,n, j=1,⋯,m );
- 异质指标同质化:在上述分析中已对指标进行了同质化处理故不再考虑
- 首先计算第 j j j项指标下第 i i i个样本值占该指标的比重
p i , j = x x , j ∑ i = 1 n x i , j , i = 1 , ⋯ , n , j = 1 , ⋯ , m p_{i,j}=\frac{x_{x,j}}{\sum_{i=1}^{n}x_{i,j}},i=1,\cdots,n,j=1,\cdots,m pi,j=∑i=1nxi,jxx,j,i=1,⋯,n,j=1,⋯,m - 然后计算第 j j j项指标的熵值
e j = − k ∑ i = 1 n p i , j l n ( p i , j ) , p = 1 / l n ( n ) > 0 , e j ≥ 0 e_j=-k\sum_{i=1}^{n}p_{i,j}ln(p_{i,j}),p=1/ln(n)>0,e_j\geq0 ej=−ki=1∑npi,jln(pi,j),p=1/ln(n)>0,ej≥0 - 计算信息熵冗余度(差异)
d j = 1 − e j , j = 1 , ⋯ , m d_j=1-e_j,j=1,\cdots,m dj=1−ej,j=1,⋯,m - 计算各项指标的权重
w j = p j ∑ j = 1 m p j , j = 1 , ⋯ , m w_j=\frac{p_j}{\sum_{j=1}^{m}p_j},j=1,\cdots,m wj=∑j=1mpjpj,j=1,⋯,m
代码如下:
import math
from numpy import array
def cal_weight(x):
'''熵值法计算变量的权重'''
# 求k
rows = x.index.size # 行
cols = x.columns.size # 列
k = 1.0 / math.log(rows)
lnf = [[None] * cols for i in range(rows)]
# 矩阵计算-- 信息熵 p=array(p)
x = array(x)
lnf = [[None] * cols for i in range(rows)]
lnf = array(lnf)
for i in range(0, rows):
for j in range(0, cols):
if x[i][j] == 0:
lnfij = 0.0
else:
p = x[i][j] / x.sum(axis=0)[j]
lnfij = math.log(p) * p * (-k)
lnf[i][j] = lnfij
lnf = pd.DataFrame(lnf)
E = lnf
d = 1 - E.sum(axis=0)# 计算冗余度
w = [[None] * 1 for i in range(cols)]# 计算各指标的权重
for j in range(0, cols):
wj = d[j] / sum(d)
w[j] = wj# 计算各样本的综合得分,用最原始的数据
w = pd.DataFrame(w)
return w
w = cal_weight(trans_data.iloc[:,1:]) # 调用cal_weight
w.index = trans_data.columns.tolist()[1:]
w.columns = ['weight']
print(w)
print('运行完成!')
weight
GDP 0.272662
人均可支配收入 0.012789
城市化水平 0.012700
户籍人口数量 0.186742
商品房销售均价 0.035685
商品房销售面积 0.317972
人均使用面积 0.018868
商品房施工面积 0.096012
供求风险 0.016948
购买力风险 0.029620
运行完成!
score=np.dot(trans_data.iloc[:,1:],w)
score=pd.DataFrame(score)
score.columns = ['熵权值法得分']
score['城市']=data['城市']
score=score[['城市','熵权值法得分']]
score['熵权值法排名']=score['熵权值法得分'].rank(ascending=False)
score
| 城市 | 熵权值法得分 | 熵权值法排名 | |
|---|---|---|---|
| 0 | 深圳 | 1.083324 | 6.0 |
| 1 | 北京 | 2.155166 | 2.0 |
| 2 | 杭州 | 1.010515 | 8.0 |
| 3 | 上海 | 2.643810 | 1.0 |
| 4 | 广州 | 1.474079 | 3.0 |
| 5 | 宁波 | 0.900653 | 10.0 |
| 6 | 天津 | 1.454370 | 4.0 |
| 7 | 南京 | 1.022953 | 7.0 |
| 8 | 苏州 | 1.153888 | 5.0 |
| 9 | 大连 | 0.875185 | 11.0 |
| 10 | 珠海 | 0.413309 | 19.0 |
| 11 | 台州 | 0.651281 | 16.0 |
| 12 | 绍兴 | 0.673925 | 13.0 |
| 13 | 常州 | 0.671696 | 14.0 |
| 14 | 南通 | 0.828544 | 12.0 |
| 15 | 无锡 | 0.900895 | 9.0 |
| 16 | 嘉兴 | 0.601033 | 17.0 |
| 17 | 舟山 | 0.352385 | 20.0 |
| 18 | 东莞 | 0.664683 | 15.0 |
| 19 | 湖州 | 0.468305 | 18.0 |
3.主成分分析
(1)变换后数据之间的相关性
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
data1=trans_data.iloc[:,1:] #定义数值型变量
import numpy as np
print(np.var(data1))
fig, ax = plt.subplots(figsize = (9,9))
corr = data1.corr()
sns.heatmap(corr, vmax=1,vmin = 0,
xticklabels= True, yticklabels= True, square=True, cmap="YlGnBu")
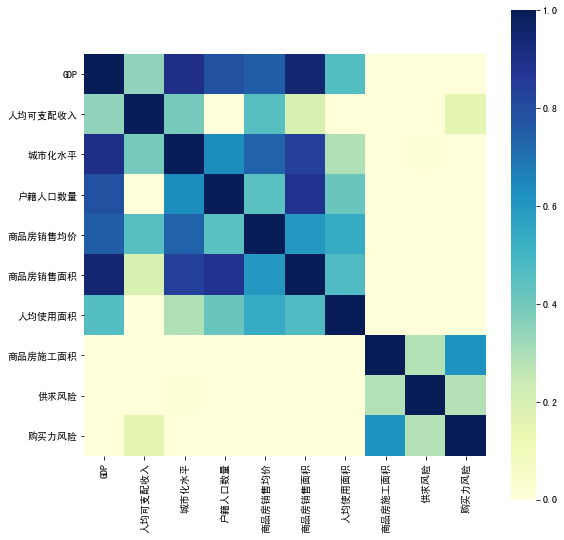
从变量的相关性分析中可以看到,有多个变量相关,首先考虑对变量进行主成分分析,且上述变量主要分了两类
from pca import pca
model = pca() # 初始化保留所有主成分
# 其他形式 model = pca(n_components=2)保留两个主成分 model = pca(n_components=0.95)方差贡献度达95%为止
data2=trans_data.iloc[:,1:]# 数据准备index为城市名,其余列保留
data2.index=data.iloc[:,0]
results = model.fit_transform(data2)#拟合
fig, ax = model.plot()# 画出累计方差贡献度图,选取两个主成分比较合适
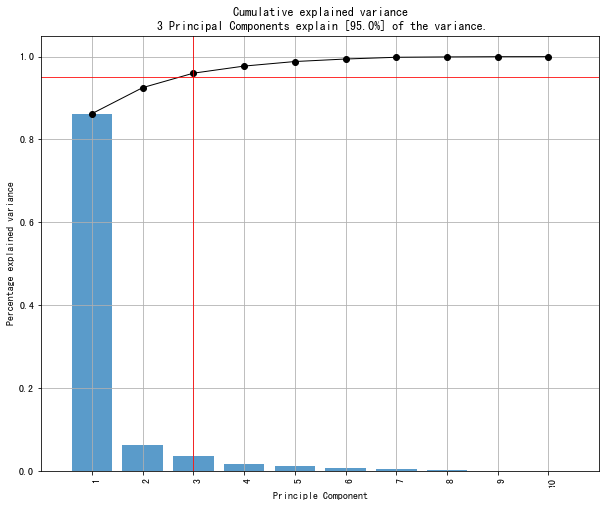
从结果中可以看到,两个主成分就可以解释95%的变异,所以保留两个主成分进行后续分析
model = pca(n_components=2)
results = model.fit_transform(data2)#拟合
fig, ax = model.scatter()# 前两个主成分画图
fig, ax = model.biplot(n_feat=4)# Make biplot with the number of features
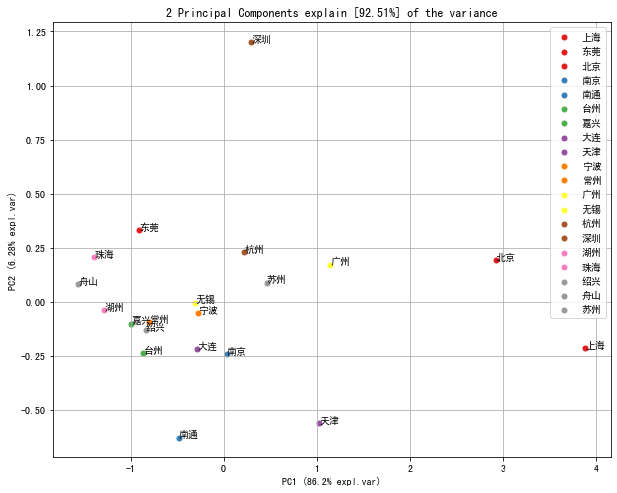
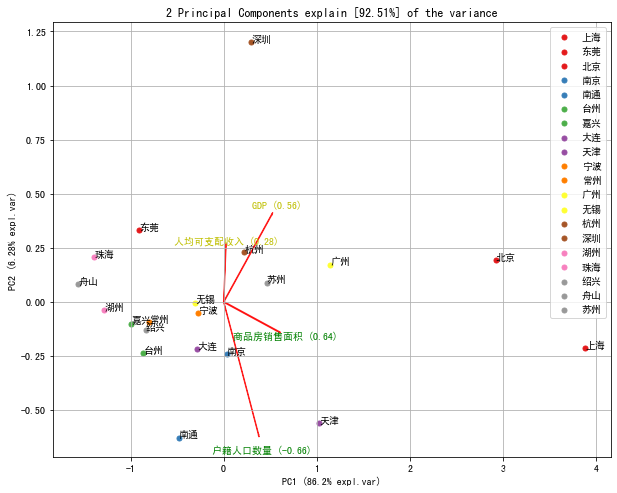
(2)主成分法结果
采用对各个主成分对方差的贡献程度进行加权,可以看到主成分1主要与商品房销售面积、GDP、人均使用面积、商品房施工面积有关,主成分2主要与户籍人口数量、人均可支配收入、城市化水平、商品房销售均价、供求风险、购买力风险
model.results['topfeat']
| PC | feature | loading | type | |
|---|---|---|---|---|
| 0 | PC1 | 商品房销售面积 | 0.643434 | best |
| 1 | PC2 | 户籍人口数量 | -0.659184 | best |
| 2 | PC1 | GDP | 0.555985 | weak |
| 3 | PC2 | 人均可支配收入 | 0.276068 | weak |
| 4 | PC2 | 城市化水平 | 0.127721 | weak |
| 5 | PC2 | 商品房销售均价 | 0.445650 | weak |
| 6 | PC1 | 人均使用面积 | 0.067279 | weak |
| 7 | PC1 | 商品房施工面积 | -0.259490 | weak |
| 8 | PC2 | 供求风险 | -0.195134 | weak |
| 9 | PC2 | 购买力风险 | -0.137929 | weak |
def min_max(x):
re=[(i-min(x))/(max(x)-min(x)) for i in x]
return re
# 按方差贡献计算各主成分的权重
explained_var=model.results['explained_var']
w_pca = pd.DataFrame([explained_var[0],explained_var[1]-explained_var[0]]/explained_var[1]) #累计值要扣除
w_pca.index = ['PC1','PC2']
w_pca.columns = ['weight']
print(w_pca)
#综合得分
score_pca=np.dot(pca_df,w_pca)
score_pca=pd.DataFrame(score_pca)
score_pca.columns = ['主成分分析-熵权值法得分']
score_pca['城市']=data['城市']
score_pca=score_pca[['城市','主成分分析-熵权值法得分']]
score_pca.sort_values(by='主成分分析-熵权值法得分',ascending=False)
4.因子分解
(1)巴特利球形度检验、KMO检验
print('巴特利球形度检验')
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value,p_value=calculate_bartlett_sphericity(data2)
print('卡方值:',chi_square_value,'P值', p_value)
#相关性检验kmo要大于0.5
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model=calculate_kmo(data2)
print('KMO检验:',kmo_model)
输出:
巴特利球形度检验
卡方值: 273.419703800147 P值 7.400205772134435e-35
KMO检验: 0.6117754048691861
巴特利球形度检验拒绝原假设说明变量之间存在相关性,适合做因子分析,相关性检验kmo值为0.5
from factor_analyzer import FactorAnalyzer
#因子分析
fa = FactorAnalyzer(8, rotation='varimax',method='principal',impute='mean')#初始化,方法为
fa.fit(data2)
ev, v = fa.get_eigenvalues()
print('相关矩阵特征值:',ev)
#Create scree plot using matplotlib
plt.figure(figsize=(8, 6.5))
plt.scatter(range(1,data2.shape[1]+1),ev)
plt.plot(range(1,data2.shape[1]+1),ev)
plt.title('碎石图',fontdict={
'weight':'normal','size': 25})
plt.xlabel('因子',fontdict={
'weight':'normal','size': 15})
plt.ylabel('特征值',fontdict={
'weight':'normal','size': 15})
plt.grid()# plt.savefig('E:/suishitu.jpg')
plt.show()
#确定因子个数
n_factors = sum(ev>1)
相关矩阵特征值: [5.90893406e+00 1.54019996e+00 1.27561274e+00 6.96807251e-01
3.58371733e-01 1.45974929e-01 3.72301362e-02 2.26174313e-02
9.24062839e-03 5.01113610e-03]
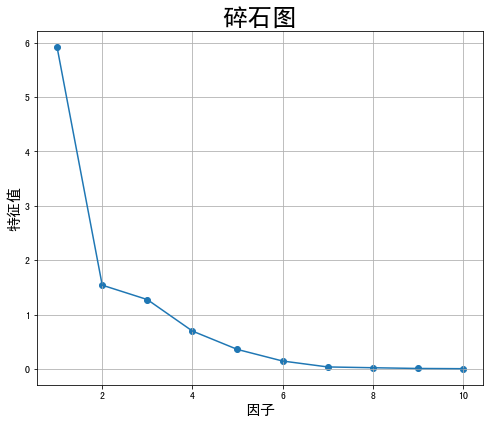
确定最优因子个数为两个,继续观察因子特征
(2)因子解释
fa2 = FactorAnalyzer(2, rotation="varimax")
fa2.fit(data2)
#fa2.loadings_
import seaborn as sns
df_cm = pd.DataFrame(np.array(fa2.loadings_), index=data2.columns)
plt.figure(figsize = (14,14))
ax = sns.heatmap(df_cm, annot=True, cmap="BuPu")
# 设置y轴的字体的大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title('Factor Analysis', fontsize='xx-large')
# Set y-axis label
plt.ylabel('指标', fontsize='xx-large')
plt.savefig('factorAnalysis.png', dpi=500)
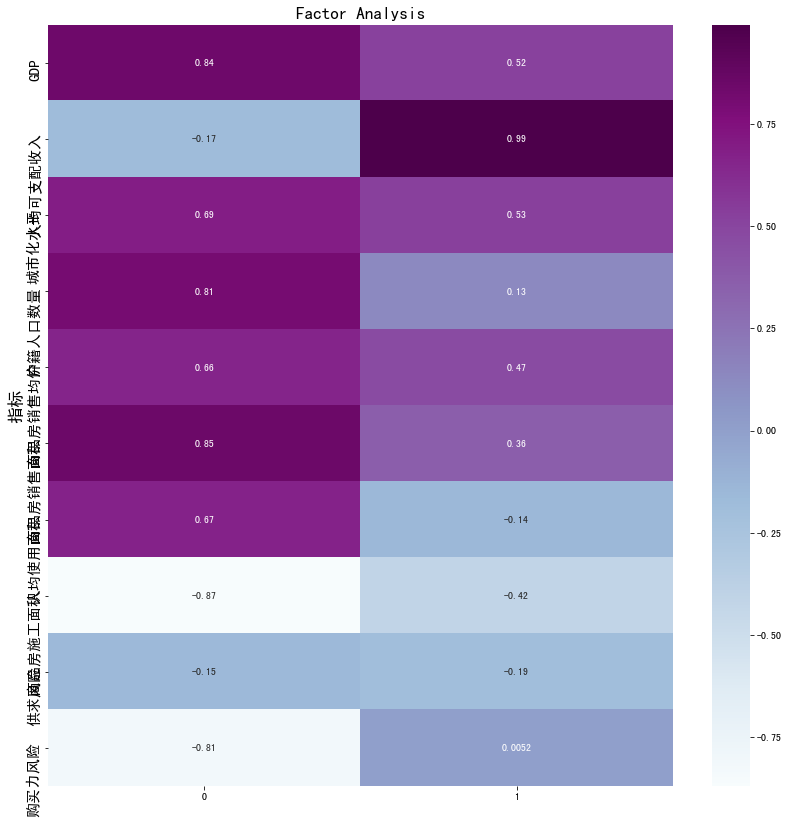
可以看到两个因子,因子一为城市总体水平相关,因子二为人均水平
(3)因子得分熵权值法
fa_result=fa2.transform(data2)
fa_df=pd.DataFrame(fa_result,columns=['因子1','因子2'])
fa_df['城市']=data['城市']
fa_df=fa_df[['城市','因子1','因子2']]
fa_df #查看各个城市因子得分情况
fa2.get_factor_variance() #三行分别为:特征值、方差贡献率、累计方差贡献率
w_fa = pd.DataFrame(fa2.get_factor_variance()[1]/fa2.get_factor_variance()[2][1]) #计算权重
w_fa.index = ['因子1','因子2']
w_fa.columns = ['weight']
print(w_fa)
print('运行完成!')
因子矩阵如下:
| 城市 | 因子1 | 因子2 | |
|---|---|---|---|
| 0 | 深圳 | 0.722835 | 0.545153 |
| 1 | 北京 | 2.047106 | 1.528530 |
| 2 | 杭州 | -0.021186 | 0.725561 |
| 3 | 上海 | 2.208202 | 0.748944 |
| 4 | 广州 | 0.971990 | 0.389431 |
| 5 | 宁波 | -0.854949 | 1.059902 |
| 6 | 天津 | 0.522120 | -0.582210 |
| 7 | 南京 | -0.286080 | 0.073427 |
| 8 | 苏州 | 0.988533 | -0.555511 |
| 9 | 大连 | 0.079789 | -0.090425 |
| 10 | 珠海 | -1.004297 | -0.118019 |
| 11 | 台州 | -0.831413 | -0.778233 |
| 12 | 绍兴 | -1.217225 | 0.628441 |
| 13 | 常州 | -0.150640 | -1.146801 |
| 14 | 南通 | 0.313035 | -1.498721 |
| 15 | 无锡 | -0.235692 | -0.519464 |
| 16 | 嘉兴 | 0.692051 | -2.635968 |
| 17 | 舟山 | -0.723960 | -0.537228 |
| 18 | 东莞 | -2.636141 | 4.229337 |
| 19 | 湖州 | -0.584076 | -1.466145 |
特征值、方差贡献率、累计方差贡献率如下:
(array([4.92525528, 2.14625952]),
array([0.49252553, 0.21462595]),
array([0.49252553, 0.70715148]))
因子权重分别为:因子1:0.696492;因子2:0.303508。
#综合得分
score_fa=np.dot(fa_df.iloc[:,1:],w_fa)
score_fa=pd.DataFrame(score_fa)
score_fa.columns = ['因子分解-熵权值法得分']
score_fa['城市']=data['城市']
score_fa=score_fa[['城市','因子分解-熵权值法得分']]
score_fa.sort_values('因子分解-熵权值法得分',ascending=False) #因子得分排序
| 城市 | 因子分解-熵权值法得分 | |
|---|---|---|
| 1 | 北京 | 0.857439 |
| 3 | 上海 | 0.846136 |
| 4 | 广州 | 0.652506 |
| 0 | 深圳 | 0.623568 |
| 8 | 苏州 | 0.613110 |
| 6 | 天津 | 0.544871 |
| 2 | 杭州 | 0.524573 |
| 9 | 大连 | 0.503017 |
| 16 | 嘉兴 | 0.478509 |
| 14 | 南通 | 0.474292 |
| 7 | 南京 | 0.457658 |
| 15 | 无锡 | 0.438691 |
| 13 | 常州 | 0.423186 |
| 5 | 宁波 | 0.419480 |
| 17 | 舟山 | 0.367706 |
| 12 | 绍兴 | 0.348320 |
| 19 | 湖州 | 0.346751 |
| 10 | 珠海 | 0.345933 |
| 11 | 台州 | 0.341602 |
| 18 | 东莞 | 0.303508 |
5.三种方法的比较
三种方法排名汇总
#score['熵权值法排名']=score['熵权值法得分'].rank(ascending=False)
score_fa['因子分解-熵权值法排名']=score_fa['因子分解-熵权值法得分'].rank(ascending=False)
score_pca['主成分分析-熵权值法排名']=score_pca['主成分分析-熵权值法得分'].rank(ascending=False)
result=score.merge(score_fa,how='left',on='城市')
result=result.merge(score_pca,how='left',on='城市')
result[['城市','熵权值法排名','主成分分析-熵权值法排名','因子分解-熵权值法排名']]
| 城市 | 熵权值法排名 | 主成分分析-熵权值法排名 | 因子分解-熵权值法排名 |
|---|---|---|---|
| 深圳 | 6.0 | 5.0 | 4.0 |
| 北京 | 2.0 | 2.0 | 1.0 |
| 杭州 | 8.0 | 7.0 | 7.0 |
| 上海 | 1.0 | 1.0 | 2.0 |
| 广州 | 3.0 | 3.0 | 3.0 |
| 宁波 | 10.0 | 9.0 | 14.0 |
| 天津 | 4.0 | 4.0 | 6.0 |
| 南京 | 7.0 | 8.0 | 11.0 |
| 苏州 | 5.0 | 6.0 | 5.0 |
| 大连 | 11.0 | 11.0 | 8.0 |
| 珠海 | 19.0 | 19.0 | 18.0 |
| 台州 | 16.0 | 16.0 | 19.0 |
| 绍兴 | 13.0 | 15.0 | 16.0 |
| 常州 | 14.0 | 13.0 | 13.0 |
| 南通 | 12.0 | 12.0 | 10.0 |
| 无锡 | 9.0 | 10.0 | 12.0 |
| 嘉兴 | 17.0 | 17.0 | 9.0 |
| 舟山 | 20.0 | 20.0 | 15.0 |
| 东莞 | 15.0 | 14.0 | 20.0 |
| 湖州 | 18.0 | 18.0 | 17.0 |
可以看到,三种方法排序略有差异,但也有共性:
- 具有较高的投资潜力(三种方法投资潜力排名前5的城市有(并集)):上海、北京、广州、深圳、天津、苏州
- 具有较差的投资潜力(三种方法投资潜力排名后5的城市有(并集)):东莞、舟山、湖州、嘉兴、珠海、台州、绍兴
- 投资潜力中等(其余):杭州、宁波、南京、大连、常州、南通、无锡
查看投资潜力较弱的城市,归纳特征:
weak_city='东莞、舟山、湖州、嘉兴、珠海、台州、绍兴'.split('、')
trans_data[trans_data['城市'].isin(weak_city)]
#trans_data为经过负向指标处理及归一化后的数据,各个均值都为1,均为越大越好
| 城市 | GDP | 人均可支配收入 | 城市化水平 | 户籍人口数量 | 商品房销售均价 | 商品房销售面积 | 人均使用面积 | 商品房施工面积 | 供求风险 | 购买力风险 |
|---|---|---|---|---|---|---|---|---|---|---|
| 珠海 | 0.222316 | 0.963882 | 0.917587 | 0.167766 | 0.869621 | 0.223202 | 0.998096 | 1.313413 | 1.034506 | 1.111000 |
| 台州 | 0.435225 | 1.038338 | 0.883602 | 1.022677 | 0.868702 | 0.324073 | 0.785967 | 1.243792 | 0.816806 | 1.181462 |
| 绍兴 | 0.497717 | 1.062883 | 0.883602 | 0.788751 | 0.827160 | 0.456687 | 0.987218 | 1.229236 | 1.054645 | 1.244216 |
| 嘉兴 | 0.397417 | 0.972446 | 0.803275 | 0.607637 | 0.790214 | 0.448576 | 0.805004 | 1.224467 | 1.015865 | 1.207275 |
| 舟山 | 0.098820 | 0.955919 | 0.803275 | 0.174920 | 0.790214 | 0.114546 | 1.074245 | 1.360495 | 1.151858 | 1.192179 |
| 东莞 | 0.778412 | 1.381105 | 1.004094 | 0.304833 | 0.770546 | 0.473444 | 0.448735 | 1.219795 | 1.039234 | 1.480923 |
| 湖州 | 0.225665 | 0.954719 | 0.818722 | 0.467074 | 0.759885 | 0.243554 | 0.943704 | 1.287424 | 0.866173 | 1.225195 |
因为三种方法来说GDP都是衡量投资潜力的重要指标,尽管这些城市商品房施工面积、供求风险、购买力风险都低于平均水平(负向指标经过逆向处理,看到的结果为越大越好,越大说明风险越低,且均值为1),但这些城市GDP较低,所以在三种方法中排序都靠后,不具有很强的投资潜力。
总结
本篇博客的主要是学习了指标排序,在无监督的情况下,如何进行排序,投资指导意义方面分析不强,20年完成的一次课程小作业。