刚体运动状态描述
空间中的刚体
空间中的刚体,要描述其状态一般需要6个参数,3个平动参数,3个转动参数,分别对应着世界直角坐标系的三个轴X,Y,Z。
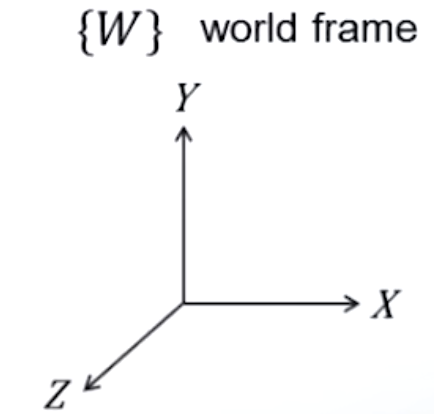
整合表达刚体的状态:在刚体上建立坐标系刚体系(body frame),坐标系的原点建立在刚体的质心上。这里需要注意的是,该坐标系的坐标轴不一定与世界直角坐标系的坐标轴平行。
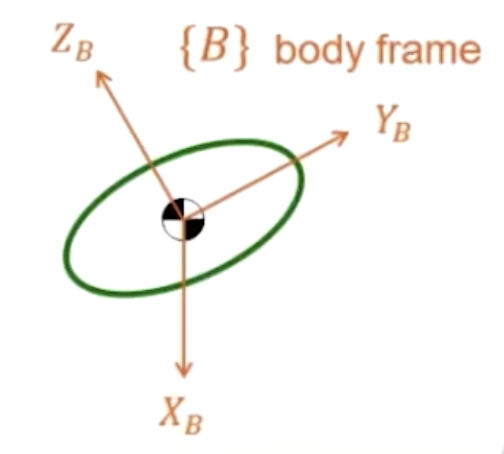
刚体平动时,由刚体系的原点位置来判定;刚体转动时,借由刚体系相比于世界坐标轴的姿态来判定。
当然这样的表述只能表述某一个时刻刚体的状态,而我们将刚体整个运动轨迹中各个时刻的这些状态参数全部记录下来
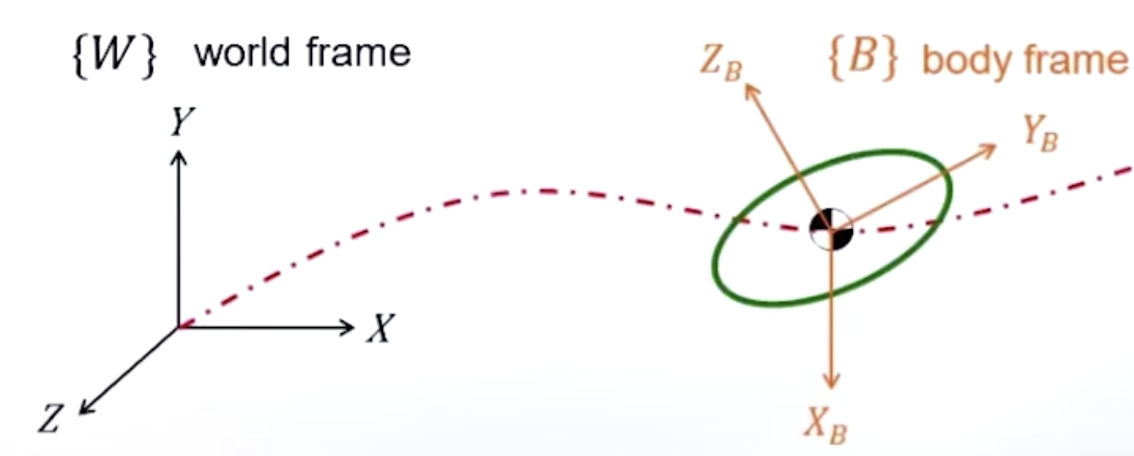
利用各个时刻平动参数对时间的微分,由位移就可以转换到速度和加速度等运动状态;利用各个时刻转动参数对时间的微分,由姿态就可以转换到角速度和角加速度等运动状态。
- 向量表达空间关系的两个方式
- 表达空间中的一个位置

- 上式表达的是某一个刚体系的原点在世界坐标系中的位置。
- 表达空间上的一个方向
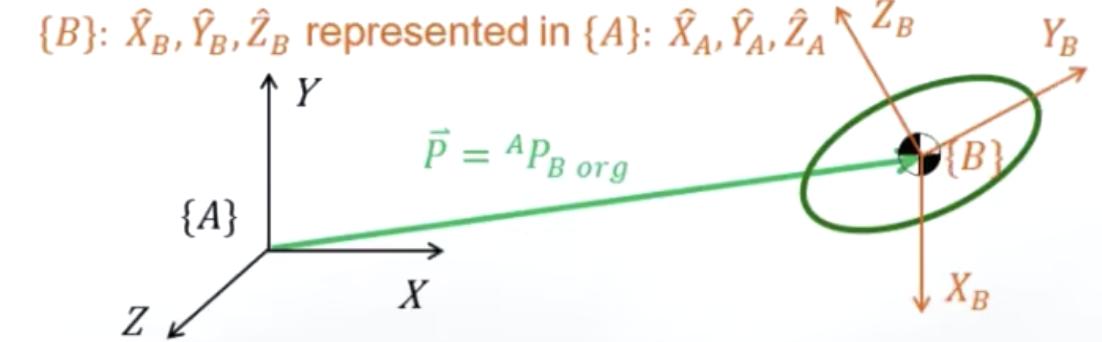
- 上图表达的是刚体系的各个轴\(X_B,Y_B,Z_B\)也可以在世界坐标系中用向量来表示,它们只表示方向,在表示方向时,一般取模为1的单位向量。
- 方向余弦(direct cosines)
方向余弦是指在解析几何里,一个向量的三个方向余弦,分别是该向量与空间直角坐标系的三个轴方向的余弦。
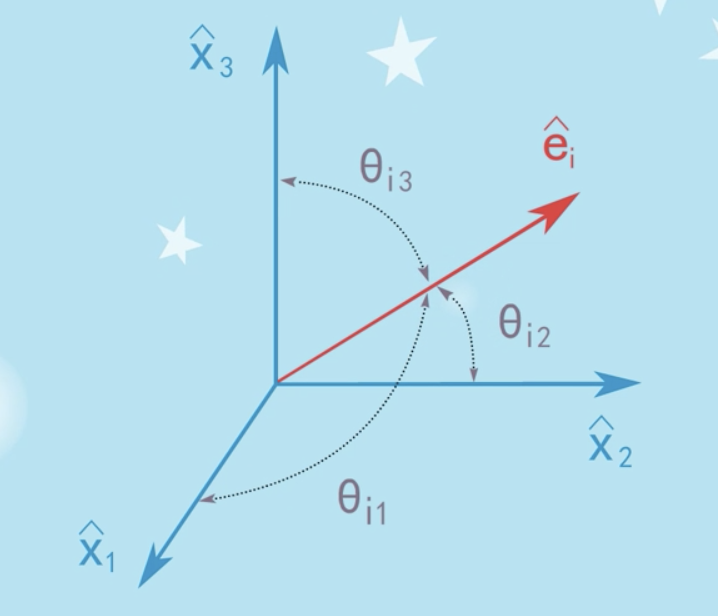
方向余弦矩阵:由两组不同的标准正交基的单位向量之间的方向余弦所形成的矩阵。可以用来表达一组标准正交基与另一组标准正交基的关系。也可以表达一个向量对另一组标准正交基的方向余弦。
- 量化表达
平动:以向量![]() 来描述刚体系{B}的原点相对于世界坐标系的状态。
来描述刚体系{B}的原点相对于世界坐标系的状态。
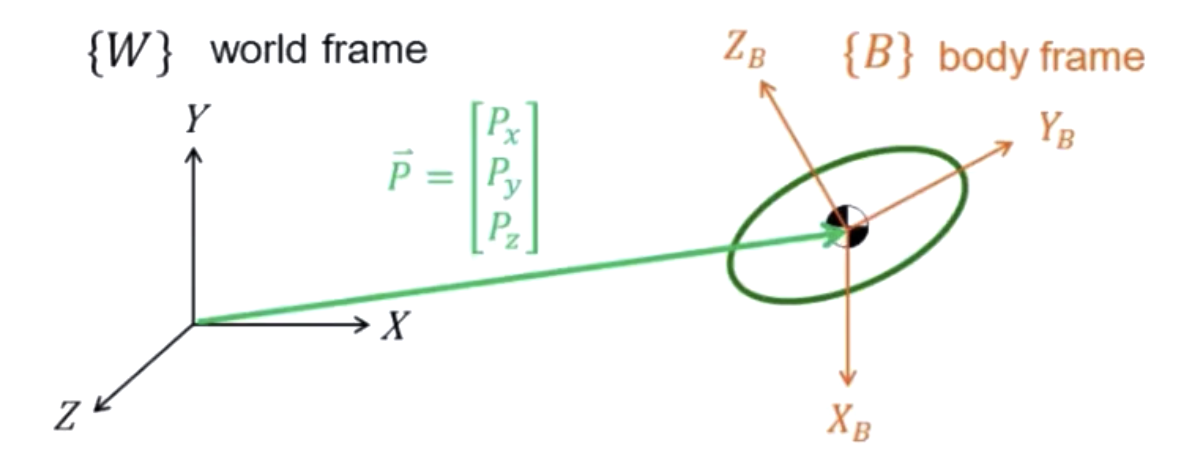
我们以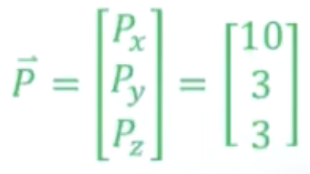 来说明
来说明
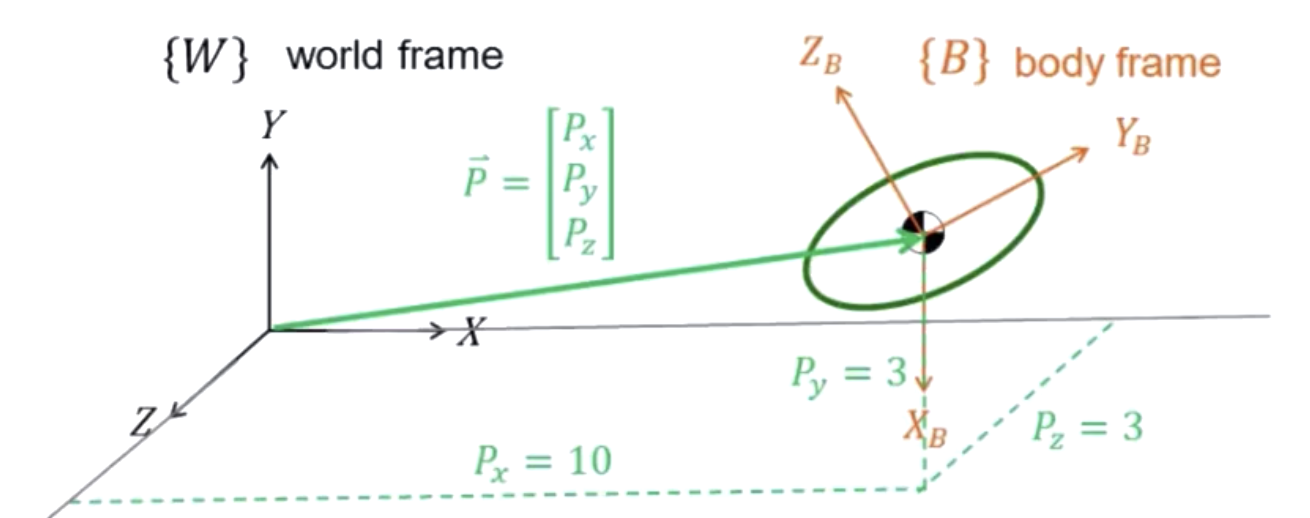
我们对{B}的原点分别向世界坐标系中做投影,它们在X、Y、Z轴上的值分别为10、3、3。
转动:描述刚体系{B}对于世界坐标系的姿态——旋转矩阵(Rotation Matrix)
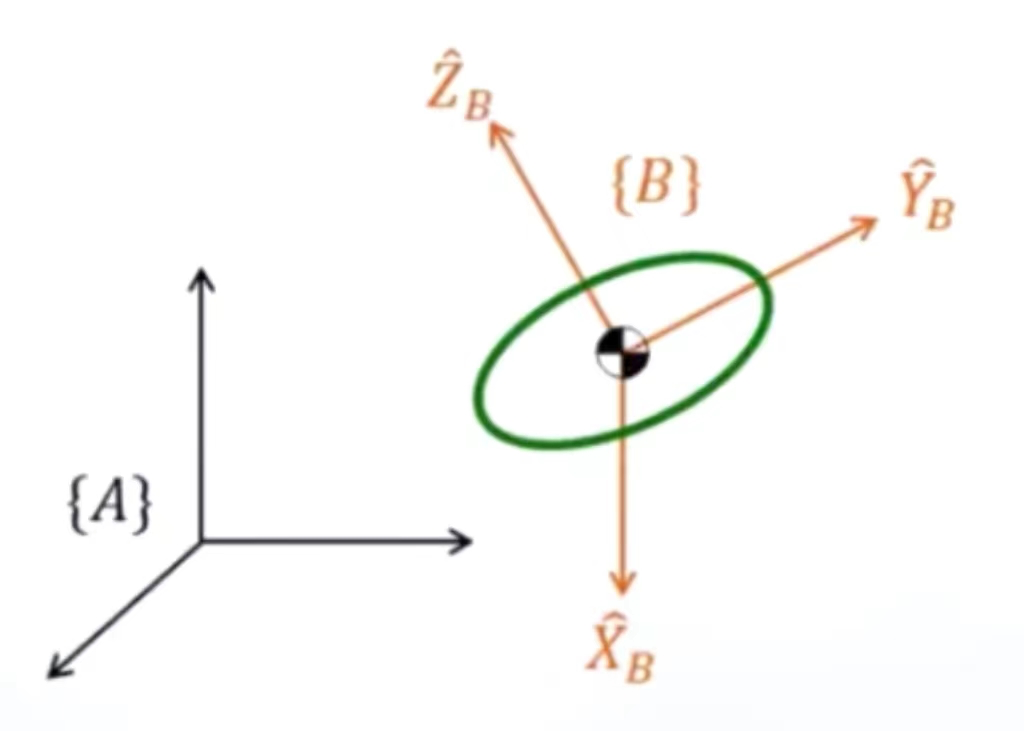
上图中,刚体系{B}的各个轴所指向的方向,可以由下式来表明
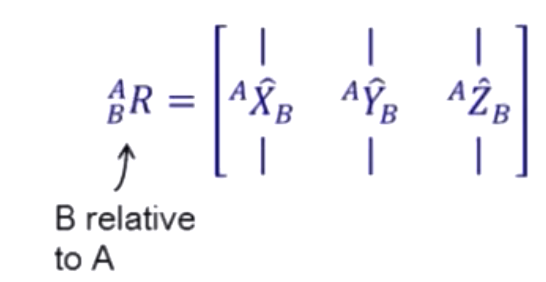
上式是一个矩阵,代表由世界坐标系{A}来表征{B},该矩阵的每一列都是3维的列向量,代表{B}各个轴在{A}中的方向,整个矩阵就是一个3*3的样式,它就是一个旋转矩阵。
R的三个列向量即为刚体系{B}的在世界坐标系{A}的基,而且是一组正交基。(有关基的概念可以参考线性代数整理 中的空间的基以及线性代数整理(二) 中的正交基与标准正交基)。我们可以使用方向余弦来表述刚体的姿态。
我们假设世界坐标系{A}的三个坐标轴的单位向量分别为\(A_1,A_2,A_3\),刚体系{B}三个坐标轴的单位向量分别为\(B_1,B_2,B_3\)。定义刚体系{B}与世界坐标系{A}坐标轴之间的方向余弦为
\(a_{ij}=cosθ_{ij}=A_i⋅B_j\)
因为\(A_i,B_j\)都是单位向量,模为1,所以上式成立。它可以表述为两个坐标系任意轴的全排列。故而
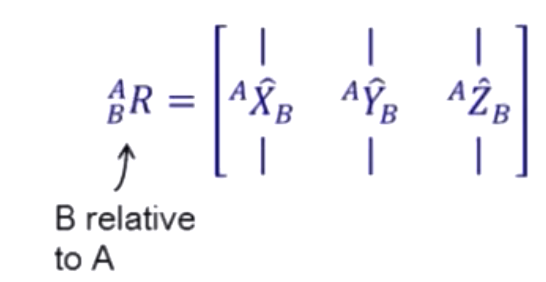
可以表述为
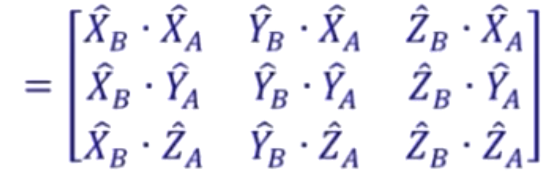
我们以下例来说明
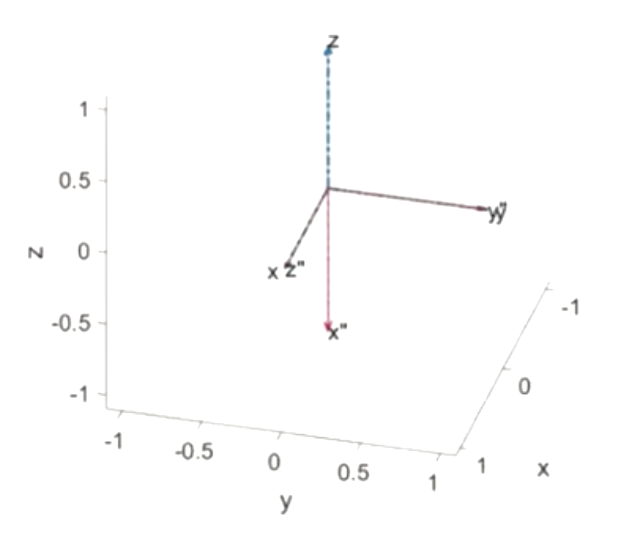
上图中,蓝色坐标系为世界坐标系{A},红色坐标系为刚体坐标系{B},现在我们要求{B}相对于{A}的姿态![]() 。
。
首先,{B}的X‘’轴与{A}的Z轴反向,故而
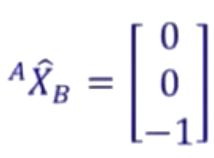
它代表{B}的X‘’轴在{A}的方向。
{B}的Y''轴与{A}的Y轴同向,故而
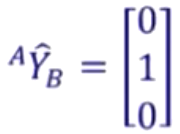
{B}的Z''轴与{A}的X轴同向,故而
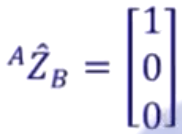
因此{B}相对于{A}的姿态为:
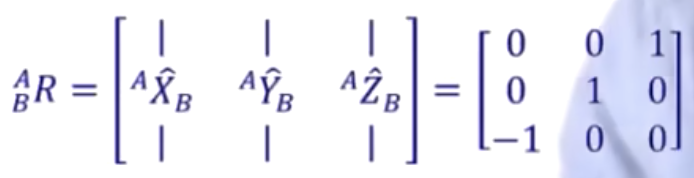
因为{A}本身的值为\((1,1,1)^T\)。
再来看一个更一般的情况。
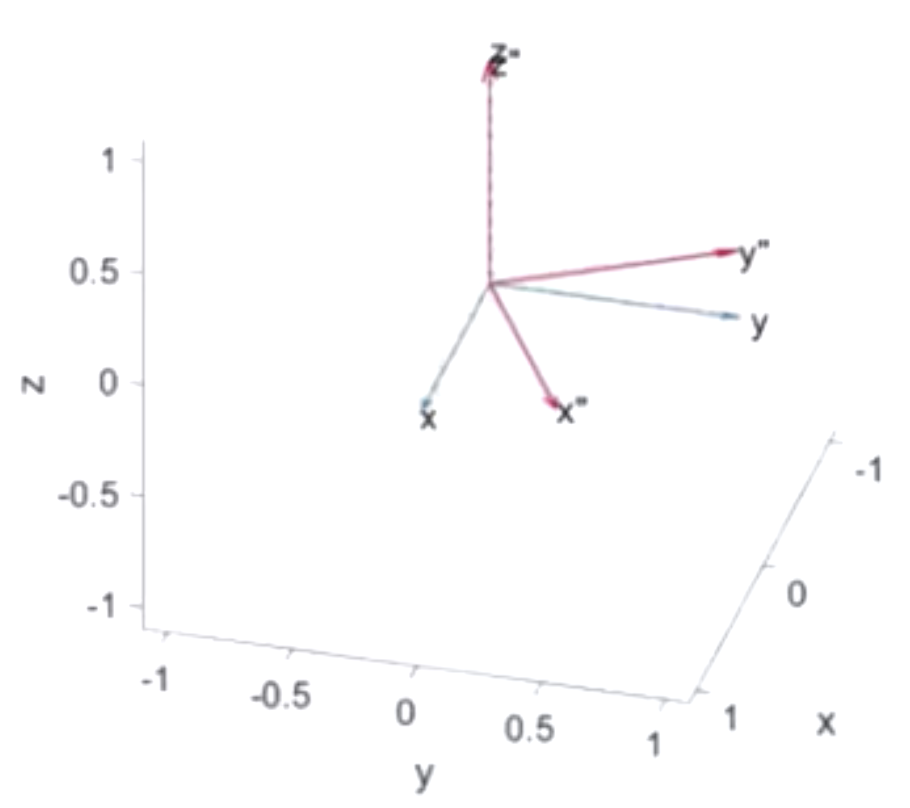
上图中,世界坐标系{A}的Z轴与刚体系{B}的Z'轴重合。那么我们来看一下它XY平面的俯视图。
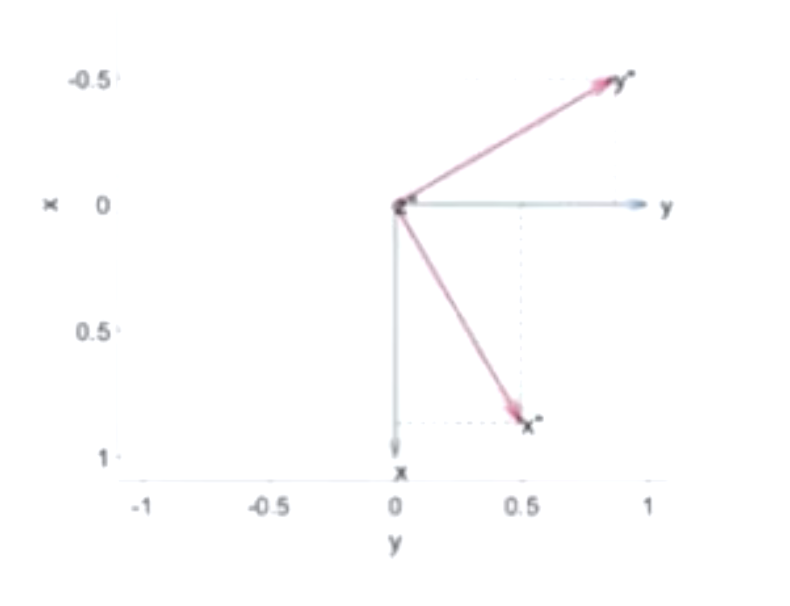
我们将刚体系{B}的\(X_B\)和\(Y_B\)分别向{A}的X轴,Y轴进行投影。那么得到的相对值就为
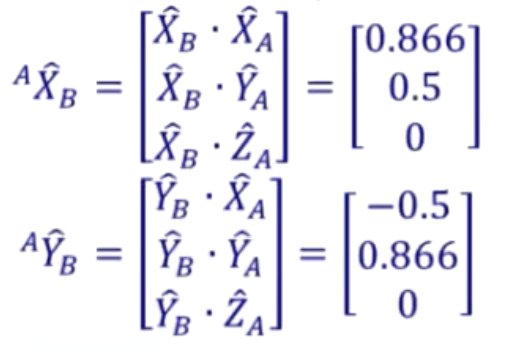
又因为Z轴重合,那么就有

那么最终可得{B}相对于{A}的姿态为

旋转矩阵
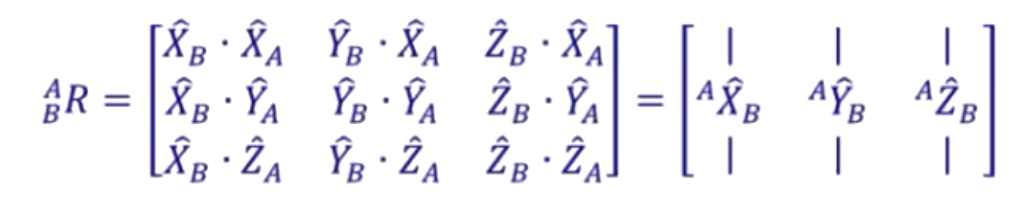
之前我们知道了该式子的含义,更进一步的,对于![]() 的点乘,我们可以理解成刚体系的X轴在世界坐标系的X轴上的投影,其他相同。
的点乘,我们可以理解成刚体系的X轴在世界坐标系的X轴上的投影,其他相同。
因为向量的点乘满足交换律,故而上式又可以写成
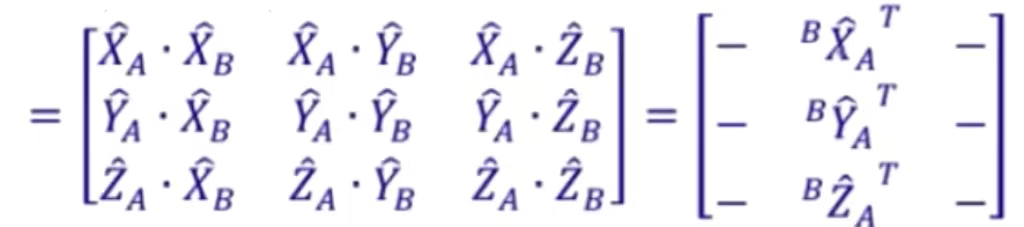
从该矩阵的行向量来看,可以看成世界坐标系的一个轴在刚体系的各个坐标轴的投影。如![]() 就可以看成是世界坐标系的X轴在刚体系的X轴的投影,其他相同。因为我们平时说的向量都是指的列向量,故而这里会写成
就可以看成是世界坐标系的X轴在刚体系的X轴的投影,其他相同。因为我们平时说的向量都是指的列向量,故而这里会写成![]() ,指的是使用刚体系{B}来表征世界坐标系{A}的X轴的转置。
,指的是使用刚体系{B}来表征世界坐标系{A}的X轴的转置。
上式又可以写成
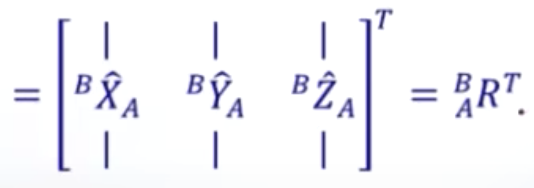
故而可以看出两个坐标系互相表征,只不过相差的就是一个转置而已。
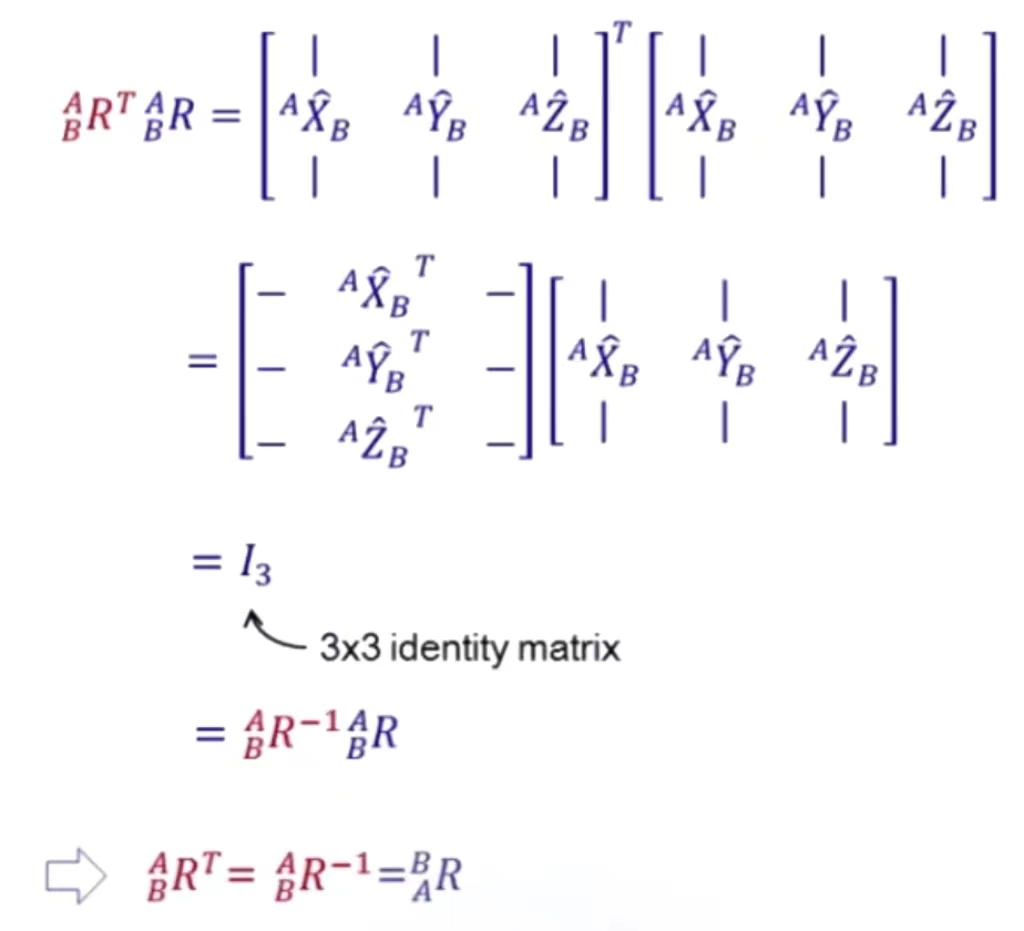
旋转矩阵的转置与它自身相乘会得到一个单位矩阵\(I_3\),这又说明它们互为可逆。(关于该部分的内容可以参考线性代数整理 中的矩阵的逆以及线性代数整理(二) 中的标准正交矩阵),这在我们对不同的坐标系进行转换的时候非常方便,只需要进行转置即可,而不需要去求矩阵的逆。
- 旋转矩阵的三种用法
- 描述一个坐标系相对于另一个坐标系的姿态。
- 将一个点由某一个坐标系的表达换到另一个跟该坐标系仅有相对转动的坐标系的表达。
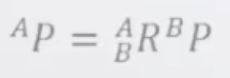
- 上式的表述为在P点在B坐标系中的位置向量左乘旋转矩阵
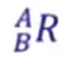 即可得到它在A坐标系中的位置向量。
即可得到它在A坐标系中的位置向量。
- 将一个点在同一个坐标系中进行转动。
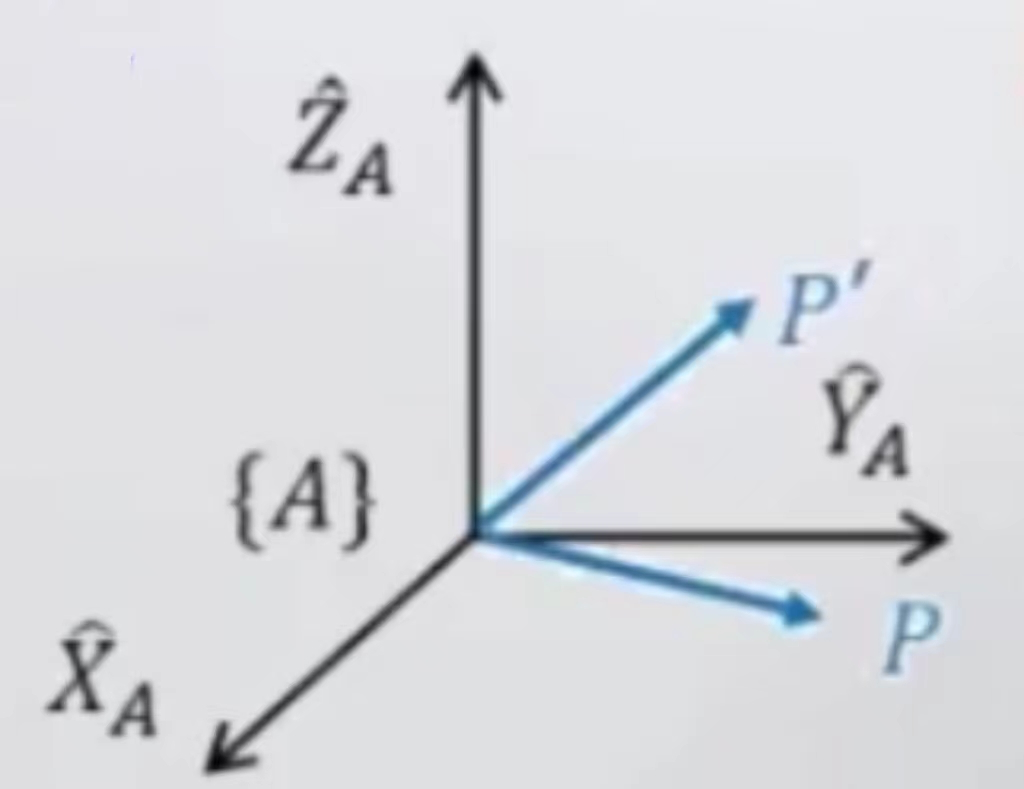
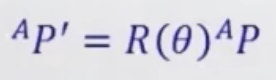
- 上式表述为P点的位置向量左乘旋转矩阵R(θ)得到它旋转到的另一个位置的位置向量,这是在同一个坐标系下进行的。
- 旋转矩阵与转角
空间中的旋转是3参数的,我们需要将旋转矩阵所表达的姿态,拆解成3次旋转角度以应对3个参数。
拆解成3次旋转需要注意的事项:
- 旋转不同于平动,平动的先后顺序可以不予计较,因为一个质点先向X方向移动,再向Y方向移动或者先向Y方向移动,再向X方向移动,效果是一样的,这种特性称为可变换的(commutable)。但是多次转动的先后顺序是需要明确化的,否则,转动后的姿态是不同的。
- 旋转的转轴也需要明确定义。是对“固定不动”的转轴旋转,还是对"转动过后的坐标系"的转轴旋转?
两种拆解方式:
- 对方向"固定不动"的转轴旋转,称为固定角度(Fixed angles)。
- 对不断转动的刚体系的转轴方向旋转(刚体系的坐标轴本身是会随时变化的),称为欧拉角度(Euler angles)。
旋转矩阵的第三种用法,可以进一步描述物体转动的状态。以旋转矩阵为基础来进行说明。
1、围绕Z轴转动
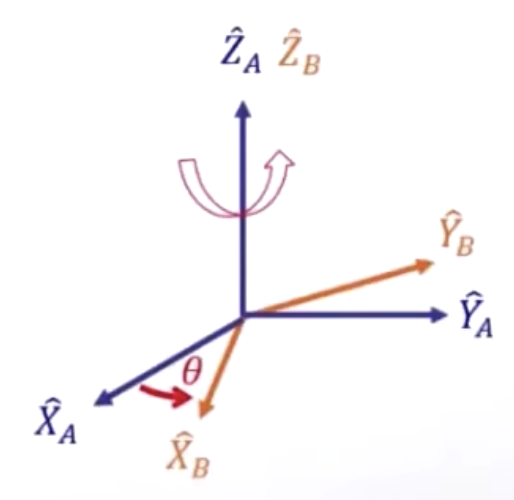
上图中蓝色的空间直角坐标系为初始状态,它围绕着Z轴逆时针旋转了一个角度θ,得到了末状态的红色的空间直角坐标系,Z轴与初始状态重合。此时的旋转矩阵为

这里简化为
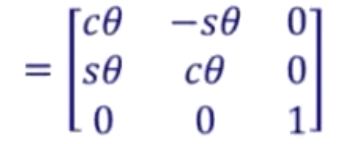
2、围绕X轴转动
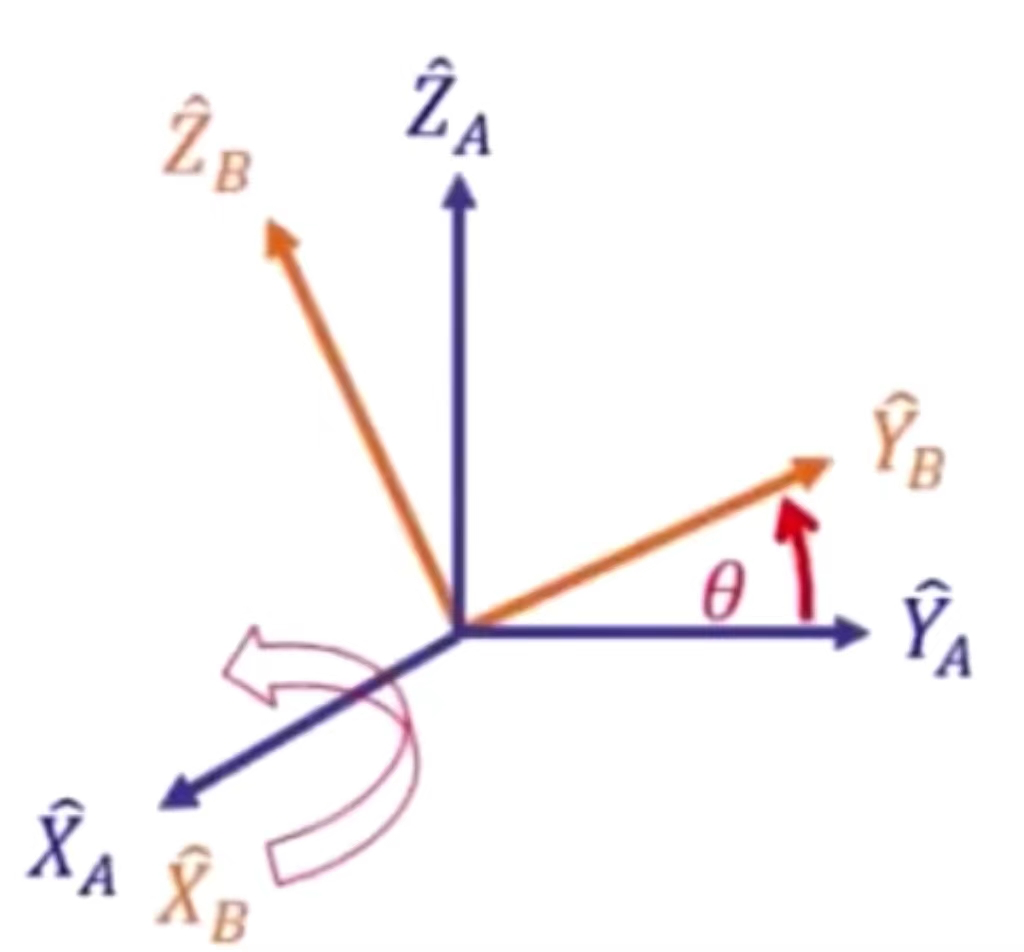
旋转矩阵为
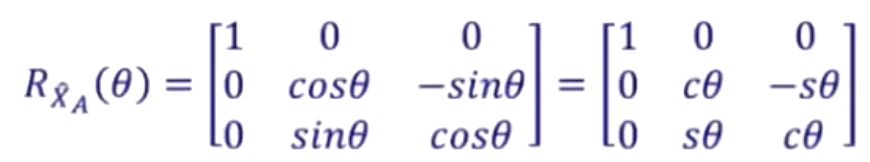
3、围绕Y轴转动
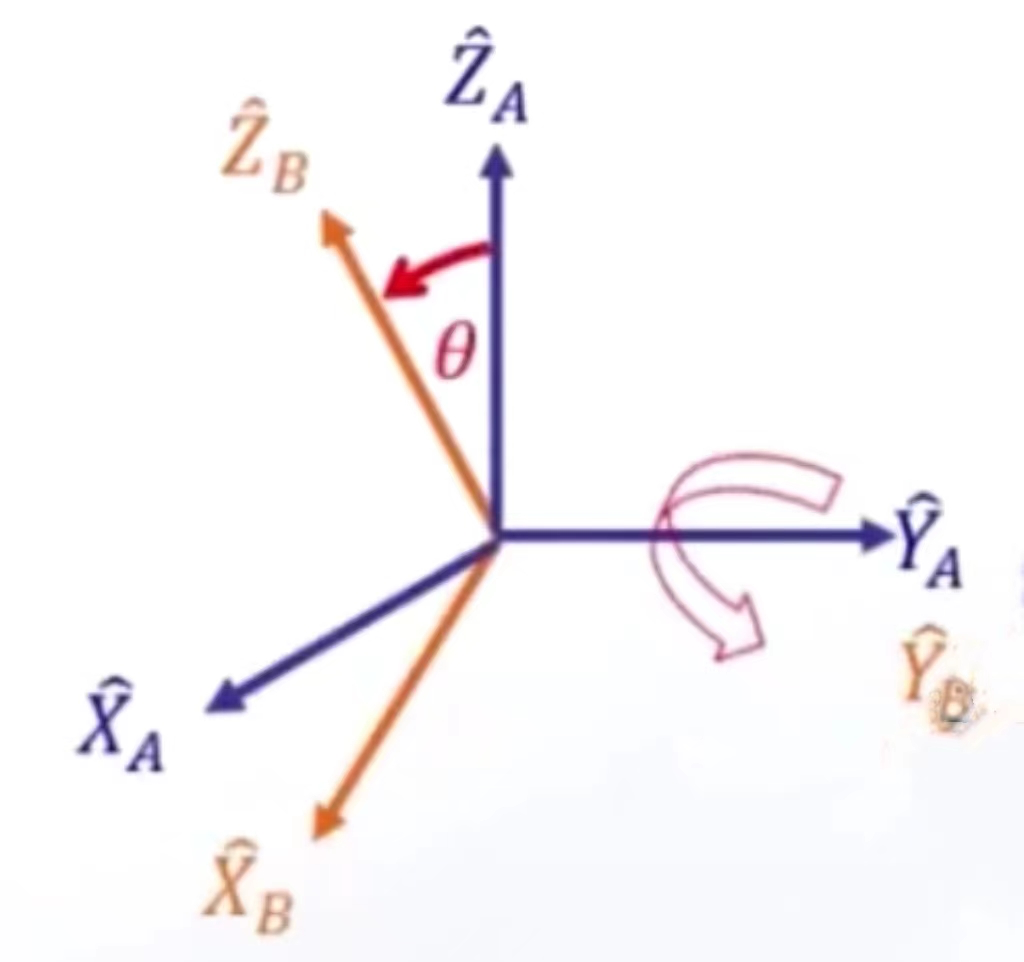
旋转矩阵为
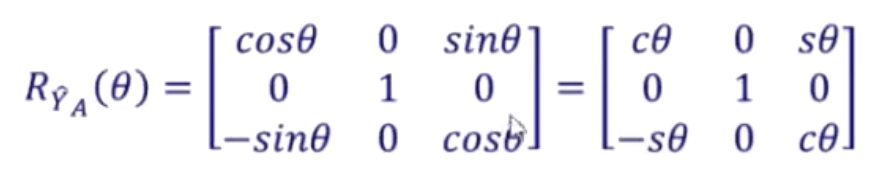
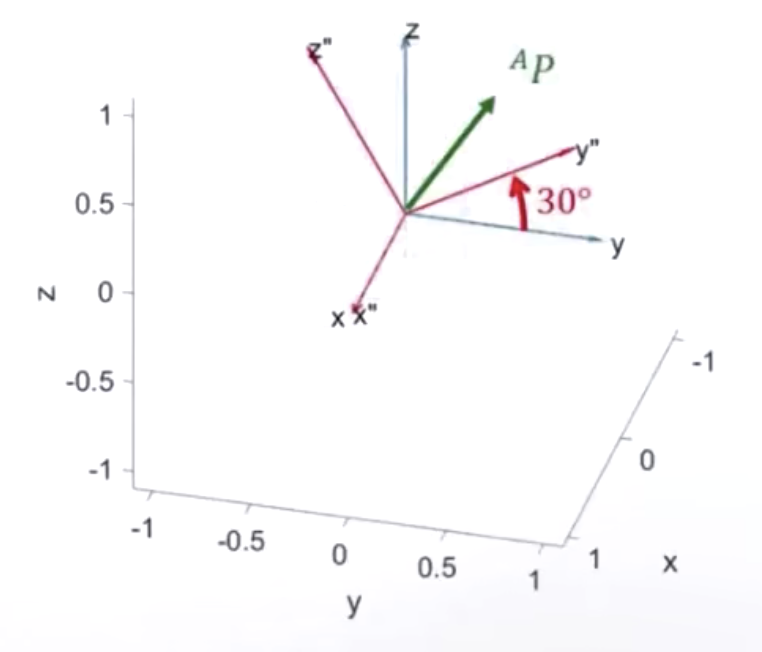
例:![]() 对
对![]() 轴旋转\(30^∘\),求
轴旋转\(30^∘\),求![]() 。
。
首先获取旋转矩阵

最后求![]()
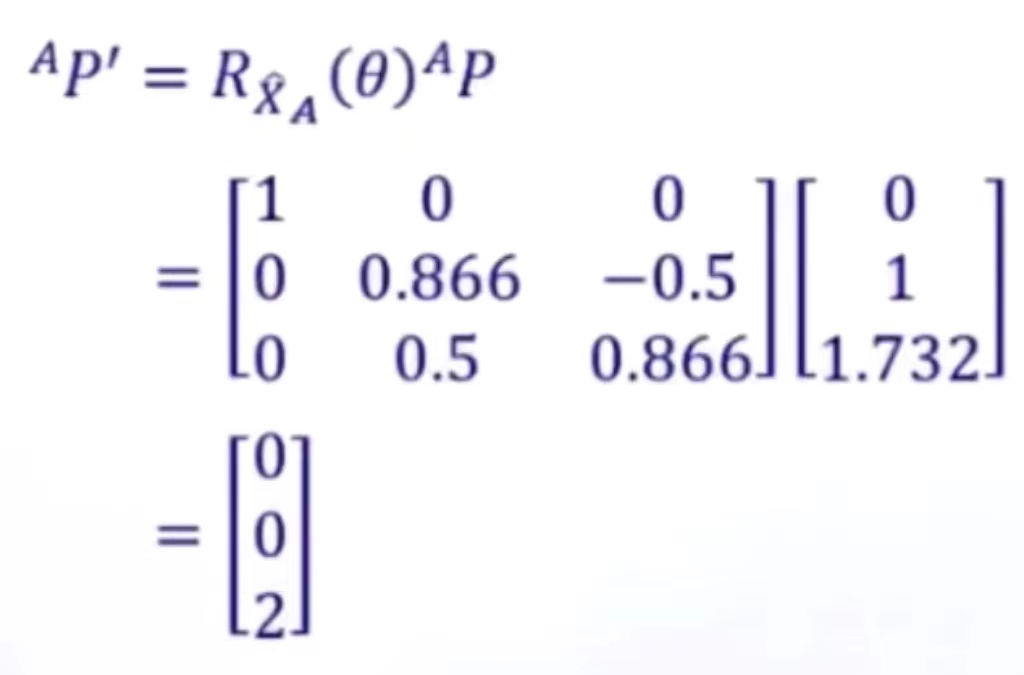
- 固定角度
这里主要是针对连续旋转
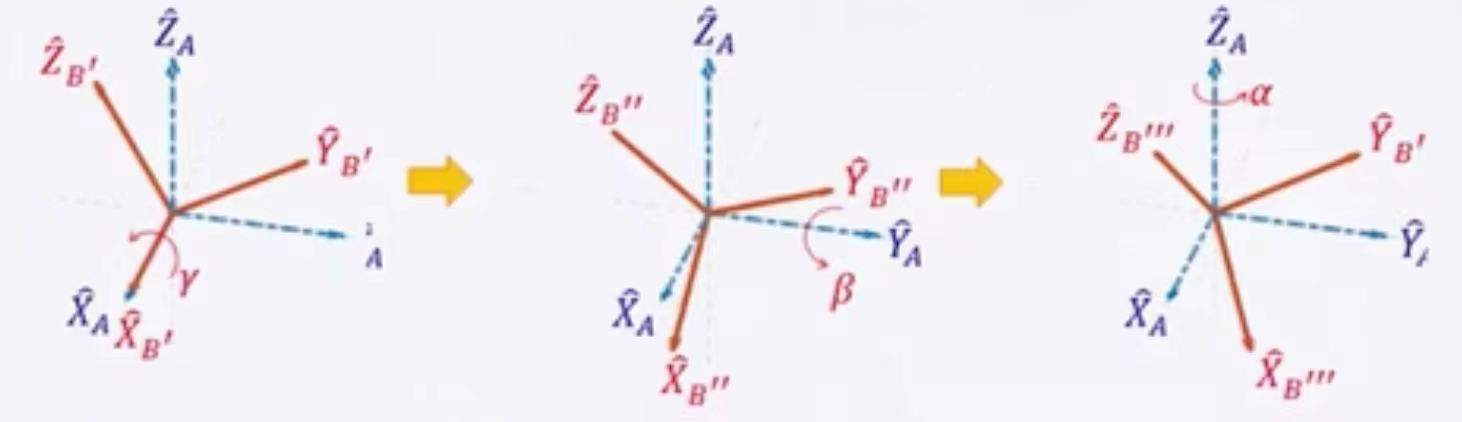
上图中定义好了空间直角坐标系{A}(蓝色虚线部分)之后,它的各个轴的方向就不再发生改变,因此被称为固定角度。
而我们的刚体坐标系{B}(红色线部分)一开始与{A}重合,然后沿着X轴逆时针旋转一个角度γ,再沿着Y轴逆时针转动一个角度β,再沿着Z轴逆时针旋转一个角度α。它最终得到的旋转矩阵,我们记为
![]()
该式的含义为围绕着X轴、Y轴、Z轴分别转动γ角、β角、α角为Z轴、Y轴、X轴三个旋转矩阵的连乘(先转的放后面,后转的放前面)。这里需要注意的是矩阵乘法是不满足乘法交换律的,所以必须要注意乘法因子的顺序。该式的结果为
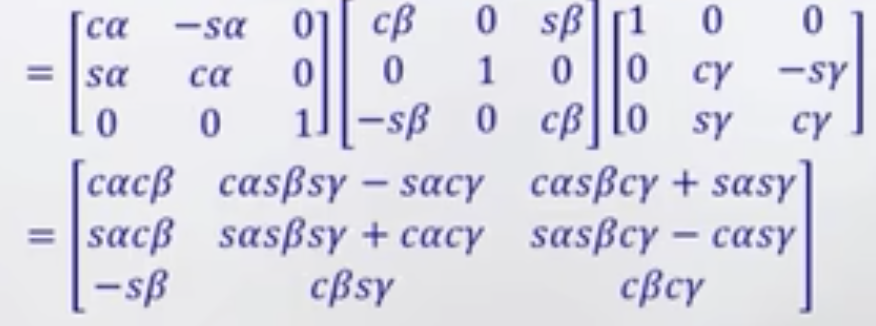
关于矩阵乘法的内容可以参考线性代数整理 中矩阵和矩阵的乘法。
例:以固定角度的方式,先对X轴旋转60度,后对Y轴旋转30度;先对Y轴旋转30度,后对X轴旋转60度,求这两次转动各自的![]() 。
。
先对X轴转60度,再对Y轴转30度
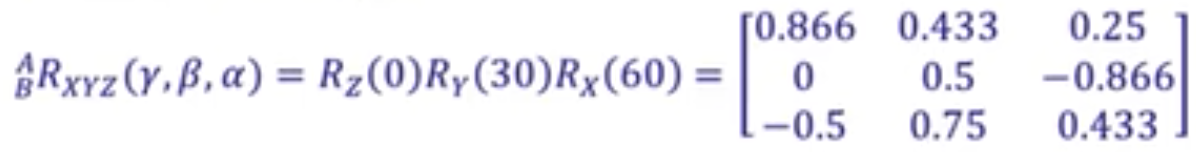
先对Y轴转30度,再对X轴转60度
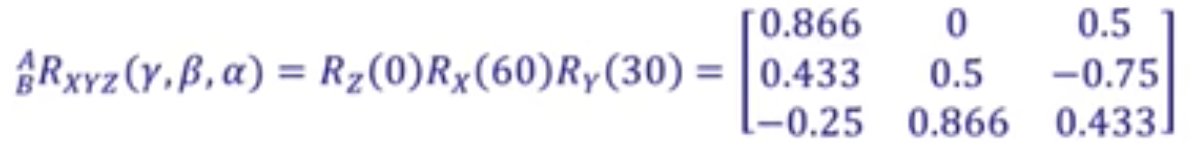
这里需要注意的是,先对Y轴转,再对X轴转不能使用之前的结果,而是需要重新去推新的计算公式。我这里推得的为

上面都是已知角度来推算旋转矩阵,现在如果已知旋转矩阵,则可以反过来推算角度。现在我们将旋转矩阵定义形式如下

可以得到,若\(β≠90^∘\)
- \(β=Atan2(-r_{31},\sqrt{r_{11}^2+r_{21}^2})\)
- \(α=Atan2({r_{21}\over cβ},{r_{11}\over cβ})\)
- \(γ=Atan2({r_{32}\over cβ},{r_{33}\over cβ})\)
如果\(β=90^∘\)
- \(α=0^∘\)
- \(γ=Atan2(r_{12},r_{22})\)
如果\(β=-90^∘\)
- \(α=0^∘\)
- \(γ=-Atan2(r_{12},r_{22})\)