摘要
在本文中,我们研究使用 Numpy 包实现卡尔曼滤波器的 Python 代码。 卡尔曼滤波分两个步骤进行:预测和更新。 每个步骤都被研究并编码为具有矩阵输入和输出的函数。 解释了这些不同的功能,并给出了用于无线网络中移动设备定位的卡尔曼滤波器应用示例。
一、简介
在可用于根据噪声传感器测量进行随机估计的重要数学工具箱中,最著名和最常用的工具之一是卡尔曼滤波器。 卡尔曼滤波器以 Rudolph E. Kalman 的名字命名,他于 1960 年发表了著名的论文,描述了离散数据线性滤波问题的递归解决方案 [3]。 卡尔曼滤波器本质上是一组数学方程,用于实现预测校正器类型估计器,该估计器在满足某些假定条件时最小化估计误差协方差的意义上是最佳的。 自推出以来,卡尔曼滤波器一直是广泛研究和应用的主题,特别是在自主或辅助导航领域。 这可能在很大程度上归因于数字计算的进步使得滤波器的使用变得实用,但也归因于滤波器本身的相对简单性和鲁棒性。 中给出了有关卡尔曼滤波的完整教程。
二. 卡尔曼滤波器的数学公式
卡尔曼滤波器解决了尝试估计由线性随机差分方程控制的离散时间控制过程的状态 x εℜ 的一般问题![]() 测量值 y ∈ℜ 即
测量值 y ∈ℜ 即![]()
随机变量 w 和 v 分别表示过程噪声和测量噪声。 假设它们彼此独立、白色且具有正态概率分布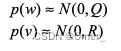
实际上,过程噪声协方差 Q 和测量噪声 R 协方差矩阵可能会随着每个时间步长或测量而变化,但这里我们假设它们是恒定的。 在没有驱动函数或过程噪声的情况下,n × 矩阵 A 将前一时间步长的状态与当前步长的状态相关联。 n ×n 矩阵 B 将可选控制输入 u ∈ℜ 与状态 x 相关联。 测量方程中的 n × m 矩阵 H 将状态与测量 y 相关联。
三.卡尔曼滤波器如何工作?
卡尔曼滤波器过程有两个步骤:预测步骤,在给定先前测量的情况下预测系统的下一个状态;以及更新步骤,在给定该时间步骤的测量的情况下估计系统的当前状态。 转化为方程如下

四.卡尔曼滤波器的应用
卡尔曼滤波在现实世界中的应用是多种多样的。 一个示例应用程序将提供有关对象位置和速度的准确、持续更新的信息,仅给出有关其位置的一系列观察结果,每个观察结果都包含一些误差。 对于一个类似的、更具体的例子,在雷达应用中,人们对跟踪目标感兴趣,在每个时刻测量有关目标的位置、速度和加速度的信息,
噪声造成的严重退化。 卡尔曼滤波器利用目标的动态特性(控制其时间演化)来消除噪声的影响,并很好地估计目标在当前时间(过滤)和未来时间(预测)的位置, 或过去的某个时间(插值或平滑)。 其他应用包括天气预报、语音增强、经济学、自动驾驶仪......
五.卡尔曼滤波器的 Python 代码
与其数学理论类似,我们选择将卡尔曼滤波代码分为两部分。 代码很简单,分为三个带有矩阵输入和输出的函数。
1. 预测步骤
此步骤必须预测时间步 k 处系统状态的均值 X 和协方差 P。 Python 函数 kf_predict 在给出六个输入时执行这些输出( X 和 P )的预测:
X : 上一步 ( k −1) 的平均状态估计。
P :上一步 ( k −1) 的状态协方差。
A : 转换 n n × 矩阵。
Q:过程噪声协方差矩阵。
B:输入效果矩阵。
U:控制输入。
该步骤的Python代码如下:
from numpy import dot
def kf_predict(X, P, A, Q, B, U):
X = dot(A, X) + dot(B, U)
P = dot(A, dot(P, A.T)) + Q
return(X,P) 2. 更新步骤
在时间步骤 k 处,此更新步骤在给定新测量值 Y 的情况下计算系统状态的后验均值 X 和协方差 P。 Python 函数 kf_update 执行 X 和 P 的更新,给出预测的 X 和 P 矩阵、测量向量 Y 、测量矩阵 H 和测量协方差矩阵 R 。 额外的输入将是:
K :卡尔曼增益矩阵
IM:Y 的预测分布的平均值
IS :Y 的协方差或预测平均值
LH :使用 Python 函数 gauss_pdf 计算的测量预测概率
from numpy import dot, sum, tile, linalg
from numpy.linalg import inv
- 4 -
def kf_update(X, P, Y, H, R):
IM = dot(H, X)
IS = R + dot(H, dot(P, H.T))
K = dot(P, dot(H.T, inv(IS)))
X = X + dot(K, (Y-IM))
P = P - dot(K, dot(IS, K.T))
LH = gauss_pdf(Y, IM, IS)
return (X,P,K,IM,IS,LH)
def gauss_pdf(X, M, S):
if M.shape()[1] == 1:
DX = X - tile(M, X.shape()[1])
E = 0.5 * sum(DX * (dot(inv(S), DX)), axis=0)
E = E + 0.5 * M.shape()[0] * log(2 * pi) + 0.5 * log(det(S))
P = exp(-E)
elif X.shape()[1] == 1:
DX = tile(X, M.shape()[1])- M
E = 0.5 * sum(DX * (dot(inv(S), DX)), axis=0)
E = E + 0.5 * M.shape()[0] * log(2 * pi) + 0.5 * log(det(S))
P = exp(-E)
else:
DX = X-M
E = 0.5 * dot(DX.T, dot(inv(S), DX))
E = E + 0.5 * M.shape()[0] * log(2 * pi) + 0.5 * log(det(S))
P = exp(-E)
return (P[0],E[0])六.应用示例:无线网络中的移动追踪
卡尔曼滤波器在电信领域最有趣的应用领域是跟踪连接到无线网络的移动用户。 在本节中,我们将介绍一种简单的跟踪算法,用于跟踪在房间内移动并连接到至少三个无线天线的移动用户。
测量矩阵 Y 描述了使用基于最小二乘估计的三边测量算法和时间步 k 处的至少三个到达时间 (ToA) 值的知识来估计移动台的位置。 这些值是使用移动设备和三个天线之间的测距程序计算的。
从不同矩阵的初始化开始,并在每个步骤和迭代中使用更新的矩阵,我们在图 1 中绘制了移动用户的估计轨迹、真实轨迹以及基于最小二乘的三边测量执行的测量结果。
我们在这里表明,与基于静态最小二乘的估计相比,卡尔曼滤波器提高了跟踪的准确性。 描述跟踪过程的Python代码如下。 为了简化这段代码的理解,我们以移动位置的真实值为中心随机绘制矩阵Y。
from numpy import *
from numpy.linalg import inv
#time step of mobile movement
dt = 0.1
# Initialization of state matrices
X = array([[0.0], [0.0], [0.1], [0.1]])
P = diag((0.01, 0.01, 0.01, 0.01))
A = array([[1, 0, dt , 0], [0, 1, 0, dt], [0, 0, 1, 0], [0, 0, 0,\
1]])
Q = eye(X.shape()[0])
B = eye(X.shape()[0])
U = zeros((X.shape()[0],1))
- 5 -
# Measurement matrices
Y = array([[X[0,0] + abs(randn(1)[0])], [X[1,0] +\
abs(randn(1)[0])]])
H = array([[1, 0, 0, 0], [0, 1, 0, 0]])
R = eye(Y.shape()[0])
# Number of iterations in Kalman Filter
N_iter = 50
# Applying the Kalman Filter
for i in arange(0, N_iter):
(X, P) = kf_predict(X, P, A, Q, B, U)
(X, P, K, IM, IS, LH) = kf_update(X, P, Y, H, R)
Y = array([[X[0,0] + abs(0.1 * randn(1)[0])],[X[1, 0] +\
abs(0.1 * randn(1)[0])]]) 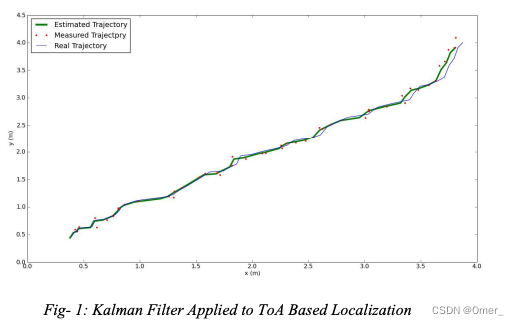
结论
在本文中,我们介绍了卡尔曼滤波器实现的 Python 代码。 我们提出了基于两步的实现,并给出了使用此类过滤器在无线网络中进行定位的示例。