1.前言
一个优秀的算法需要满足正确性、可读性、健壮性、高效性。一般前三个比较容易做到,高效性是不容易被开发人员自己发现的,效率低不可怕,可怕的是写代码的人不知道效率低。不同的算法对性能的影响是很大的,本文就高效性来探讨。
2.通过实际测试得出效率
用测试手段来精确计算出算法执行的时间。
优点:
可以得到算法具体的执行时间。
缺点:
(1)算法受不同设备的影响,不同设备跑出来的时间可能不同,最终导致得到的结果不可信;
(2)如果算法比较耗时,就得一直等着计算完了才能得到结果,比较浪费时间;
3.用理论知识事先分析得出效率
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间,有时候时间效率与空间效率是相互矛盾的,要时间则要牺牲空间,要空间则要牺牲时间,也就是常说的空间换时间/时间换空间。
在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度,本文主要讲时间复杂度。
3.1.概念:
一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
3.2.表示方法:
用大O符号(Big O notation)描述函数渐进行为,主要有以下几种复杂度:
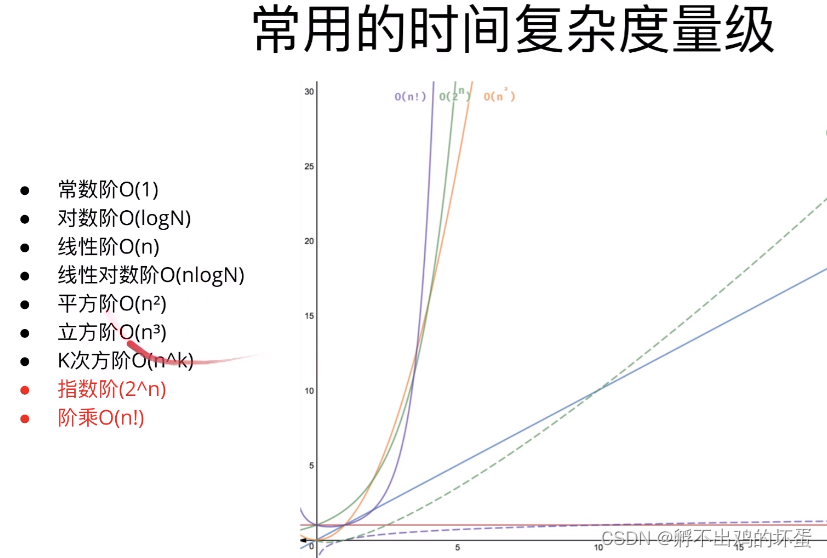
写算法时,我们应该尽量选择曲线平滑的时间复杂度。 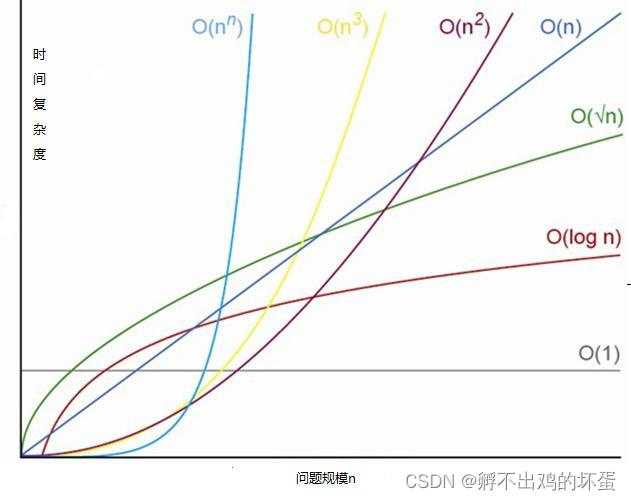
3.2.1.常数型O(1)
- 常见于赋值和引用等简单操作
- 算法消耗不随变量增长而增长,性能最佳
- 无论代码执行多少行,即使有几千几万行,时间复杂度都为O(1)
- 实际开发过程中,一次递归的时间复杂度也为O(1)。因为O(1^n)无论n为多少都为O(1)
int i = 1;
int j = 2;
i++;
j--;
int k = i + j;代码分析: i为1,j为2,k为3。 时间复杂度为O(1)。
3.2.2.对数型O(log n)
- 常用代码执行次数为x,n为目标数字。符合2^x=n,推导出x=log2(n)(log n)的情况
- 算法消耗随n的增长而增长,性能较好
int i = 100;
int j = 1;
while(j < i){
j = j * 2
}代码分析: j为128。 i为100,时间复杂度为O(log2(100))。 因为Math.log2(100)≈6.64,所以最终的时间复杂度为O(6.65)。
3.2.3.线性型O(n)
- 常见于一次for循环,while循环
- 算法消耗随n的增长而增长,性能一般
- 无论n值有多大,时间复杂度都为O(n)
int n = 100;
int j = 0;
for(int i = 0; i < n; i++){
j = i;
}代码分析: i为100,j为99。 n为100,时间复杂度为O(100)。
3.2.4.线性对数型O(n log n)
- 常用于一个对时间复杂度为O(log2(n))的代码执行一个n次循环
- 算法消耗随n的增长而增长,性能较差
int n = 100;
for(int m = 0; m < n; m++){
int i = 1;
while(i < n){
i = i * 2
}
}代码分析: i为128。 m为100,n为100,时间复杂度为O(m log2(n))。 因为100* Math.log2(100)≈664.39,所以最终的时间复杂度为O(664.39)。
3.2.5.平方型O(n^2)、立方型O(n^3)、K次方型O(n^k)
- 最常见的算法时间复杂度,可用于快速开发业务逻辑
- 常见于2次for循环,或者3次for循环,以及k次for循环
- 算法消耗随n的增长而增长,性能糟糕
- 实际开发过程中,不建议使用K值过大的循环,否则代码将非常难以维护
int n = 100
int v = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
v = v + j + i;
}
}代码分析: v为990000,i为100,j为100. n为100,时间复杂度为O(100^2)。 也就是O(10000)。
立方型O(n^3)、K次方型O(n^k)和平方型O(n^2)类似,无非是多了几次循环。
// 立方型O(n^3)
for(int i =0; i < n; i++){
for(int j = 0; j < n; j++){
for(int m = 0; m < n; m++){
}
}
}
// K次方型O(n^k)
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
for(int m = 0; m<n; m++){
for(int p = 0; p < n; p++){
... // for循环继续嵌套下去,k值不断增大
}
}
}
}3.2.6.阶乘型O(n!)
- 极其不常见
- 算法消耗随n的增长而增长,性能极其糟糕
void method(n) {
for(int i = 0; i < n; i++) {
method(n-1);
}
}阶乘型O(n!)的时间复杂度按照(n!+(n-1)!+(n-2)!+ ··· + 1) +((n-1)!+(n-2)!+ ··· + 1)+ ··· 的方式去计算。