《数值分析》-1-求解方程

0.背景

方程求解是工程计算中最重要的问题之一，本章主要介绍确定方程 $f(x)=0$ 解x的不同方法。

为什么需要了解多于一种的方程求解方法？方法的选择依赖于对函数 $f$ 或者其导数求值所需的代价，不同的使用场景对求解方法的收敛速度与计算复杂度需求不同。

前向误差与反向误差

我们为 $f(x)=0$ 方程求解得出的近似解为 $x_a$ ，方程的精确解为 $r$

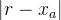
前向误差： $\left | r-x_a \right |$

后向误差： $\left | f(x_a) \right |$

后向误差在垂直方向进行度量，通常比在水平方向度量的前向误差要小很多。

方程求解方法的终止条件可以基于前向或者后向误差。

敏感性问题

如果在输入中是一个小误差，在这种情况下对问题进行求解，造成输出中的大问题，这样的问题被称为敏感性问题。假设对输入做了个小变化 $\varepsilon g(x)$

根的敏感公式： $\triangle r=-\frac{\varepsilon g(r) }{f'(r)}=-\frac{g(r) }{f'(r)}\varepsilon$

$\varepsilon$ 前的系数为误差放大因子，定义为{相对前向误差}/{相对后向误差}

1.二分法

主要思想

依据中值定理，先大概确定根的位置，判断它是位于现有区间的左半部分还是右半分，然后再进一步细分根所在的区间。

具体算法

假设初始区间是 $[a,b]$ ，在n次二分之后，得到的区间是 $[a_n,b_n]$ 的长度为 $(b-a)/2^n$ ，选择中点 $x_c=(a_n+b_n)/2$ 作为值的最优估计值。

定理

如果误差小于 $0.5\cdot 10^{-p}$ ，解精确到小数点后 $p$ 位。

特点

在二分迭代的过程中，并不需要知道函数的整个曲线，只需要在必要的位置计算函数的值。

对于二分法，确定了期望的精度就可以通过定理计算得到必须的迭代次数。

2.不动点迭代FPI

定义

当 $g(r)=r$ ，实数 $r$ 就是函数 $g$ 的不动点。

主要思想

所有的方程 $f(x)=0$ 都可以转换为一个形如 $f(x)=x$ 的不动点迭代问题，而且同一方程可以有多种转化形式，有些转化形式可以收敛到不动点，而有些形式则无法收敛。本质上是误差的线性收敛与发散问题。

具体算法

首先将 $f(x)=0$ 改写成一个合适的 $g(x)=x$ 的形式；

给定 $x_0$ =初始估计；

执行 $x_{i+1}=g(x_i)$ ;

直到 $\left | x_{i+1}-x_i \right |<TOL$

定理

假设函数 $g$ 是连续可微函数， $g(r)=r$ ， $S=\left | g'(r) \right |<1$ ，则不动点迭代对于一个足够接近 $r$ 的初始估计，以速度 $S$ 线性收敛到不动点 $r$ .

特点

二分法可以保证线性收敛，不动点迭代仅仅是局部收敛，当不动点迭代收敛时，其线性收敛。二分法在每一步中可以去除1/2的不确定性，而在FPI中，不确定性每步会乘上 $S=\left | g'(r) \right |$ ，因此，不动点迭代可能比二分法更快或者更慢，取决于S于1/2的大小关系。

并且，不动点迭代法，并不能保证一定能够收敛到 $r$ .

3.牛顿法

牛顿法是FPI的一种改进算法，也称牛顿-拉夫逊方法。

主要思想

从 $x_0$ 开始，画出函数 $y=f(x)$ 的切线，和x轴的交点记做 $x_1$ ，将其作为函数根的下一个近似，重复整个过程。

具体算法

$x_0$ =初始值；

$x_{i+1}=x_{i}-\frac{f(x_i)}{f'(x_i)}$

...

定理

假设函数 $f$ 是二阶连续可微函数， $f(r)=0$ ,如果 $f'(r)\neq 0$ ，则牛顿法局部二次收敛到 $r$ ，第 $i$ 步的误差 $e_i$ 满足:

$lim_{t\rightarrow \infty } \frac{e_{i+1}}{e_i^2}=M$

其中，

$M=\frac{f''(r)}{2f'(r)}$

特点

牛顿方法并不是总能二次收敛，在多重根位置上它是线性收敛的，其中线性收敛系数 $S=(m-1)/m$ 。

其中m重根定义为：

如果 $0=f(r)=f'(r)=...=f^{(m-1)}(r)$ ，但是 $f^{(m)}(r)=0$ .

4.割线法及其变体

牛顿法之所以能够达到较快的迭代速度是因为使用了更多的信息，尤其是通过函数导数得到的函数切线方向的信息。但在某些情况下，可能难以计算导数，在这种情况下，割线方法就是牛顿方法的平替，它使用了近似值割线代替切线，并且收敛速度差不多快。

割线方法具体过程

$x_0,x_1$ =初始估计

$x_{i+1}=x_{i}-\frac{f(x_i)(x_i-x_{i-1})}{f(x_i)-f(x_{i-1})}$

使用差商代替了导数，因此该方法需要两个初始估计。

割线法有三种推广形式：试位法、Muller方法、逆二次差值法IQI。

试位法具体过程

给定区间 $[a,b]$ ,使得 $f(a)(b)<0$

$for\, i=1,2,3...$

         $c=\frac{bf(a)-af(b)}{f(a)-f(b)}$

         $if f(c)=0,stop,end$

$if f(a)f(c)<0$

$b=c$

   $else$

                 $a=c$

         $end$

$end$

可以看出，试位方法主要思想是不断更新含根区间，它开始表现得比二分法和割线法都要好，具有二者最好的性质，但是不能保证像二分法一样在每一步确保消除1/2不确定性。

Muller方法与逆二次差值法IQI

这两种方法都是使用抛物线替换直线的思路(都需要三个初始估计进行抛物线插值)，区别在于Muller方法采用的抛物线形式为 $y=p(x)$ 会与x轴有多个交点，而逆二次差值法IQI采用的抛物线形式为 $x=p(y)$ 只会与x轴有一个交点。