Notes
## 分治思想和递归表达式
【分治思想】
将一个问题分解为与原问题相似但规模更小的若干子问题,递归地解这些子问题,然后将这些子问题的解结合起来构成原问题的解。这种方法在每层递归上均包括三个步骤:
- divide(分解):将问题划分为若干个子问题
- conquer(求解):递归地解这些子问题;若子问题Size足够小,则直接解决之
- Combine(组合):将子问题的解组合成原问题的解
【分治递归表达式】
- 设T(n)是Size为n的执行时间,若Size足够小,如n ≤ C (常数),则直接求解的时间为θ(1)
- ①设完成划分的时间为D(n)
- ②设分解时,划分为a个子问题,每个子问题为原问题的1/b,则解各子问题的时间为aT(n/b)
- ③设组合时间C(n)
- 则有递归方程总结为:
- T(n)=θ(1) if n<c
- T(n)=aT(n/b)+D(n)+C(n) if n≥c
- 技术细节(注意):
- 在声明、求解递归式时,常常忽略向上取整、向下取整、边界条件
- 边界条件可忽略,这些细节一般只影响常数因子的大小,不改变量级。求解时,先忽略细节,然后再决定其是否重要!
## 求解递归式的方法
【代入法】
- 代入法求解分为两步:
- 猜测解的形式
- 用数学归纳法求出解的常数C,并证明正确性,关键步骤是用猜测的解代入到递归式中。
-
做出好的猜测(没有一般方法,只能凭经验)
-
与见过的解类似,则猜测之。

-
先证较宽松的上、下界,减小猜测范围。我们可以从下界Ω(n)开始,上界O(n^2),然后逐渐收敛至(nlog2n)
-
- 细节修正
- 有时猜测解是正确的,但数学归纳法却不能直接证明其细节,这是因为数学归纳法不是强大到足以证明其细节。
- 这时可从猜测解中减去一个低阶项以使数学归纳法得以满足
-
避免陷阱
-
与求和式的数学归纳法类似,证明时渐近记号的使用易产生错误。
- 如:证明O(n)时必须严格证明≤cn,不能讲其换做cn+n
-
-
变量变换
-
有时改动变量能使未知递归式变为熟悉的式子。例如:

-
【代入法例题】
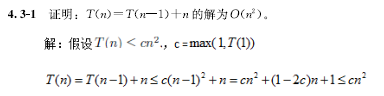


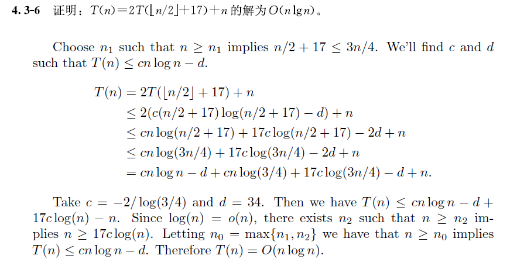
【递归树法】
- 递归树最适合用来生成好的猜想,然后可用代入法来验证猜测是否正确
- 需要关注:
- 达到边界条件所需的迭代次数
- 迭代过程中的和式。若在迭代过程中已估计出解的形式,亦可用代入法
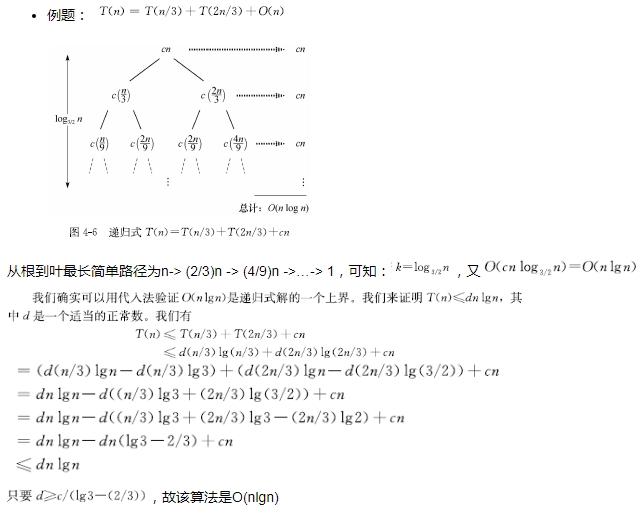
【递归树法例题】
![]()