现代C++中的从头开始深度学习:成本函数

一、说明
在机器学习中,我们通常将问题建模为函数。因此,我们的大部分工作都包括寻找使用已知模型近似函数的方法。在这种情况下,成本函数起着核心作用。
这个故事是我们之前关于卷积的讨论的续集。今天,我们将介绍成本函数的概念,展示常见示例并学习如何编码和绘制它们。与往常一样,从头开始纯C++和本征。
二、关于本系列
在本系列中,我们将学习如何仅使用普通和现代C++对必须知道的深度学习算法进行编码,例如卷积、反向传播、激活函数、优化器、深度神经网络等。

这个故事是:C++中的成本函数
...更多内容即将推出。
三、机器学习中的建模
作为人工智能工程师,我们通常将每个任务或问题定义为一个功能。
例如,如果我们正在开发一个人脸识别系统,我们的第一步是将问题定义为将输入图像映射到标识符的函数:

对于医疗诊断系统,我们可以定义一个函数来将症状映射到诊断:

我们可以编写一个模型来提供给定单词序列的图像:
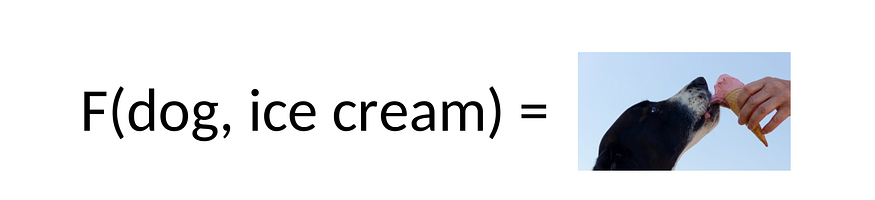
这是一个无穷无尽的清单。使用函数来表示任务或问题是实现机器学习系统的简化方法。
问题往往是:如何知道 F() 公式?
四、近似函数
事实上,使用公式或规则序列定义F(X)是不可行的(有一天我将解释原因)。
一般来说,我们不是找到或定义正确的函数 F(X),而是尝试找到 F(X) 的近似值。 让我们通过假设函数来称这种近似,或者简单地称为H(X)。
乍一看,这没有意义:如果我们需要找到近似函数 H(X),为什么我们不尝试直接找到 F(X)?
答案是:我们知道H(X)。虽然我们对F(X)知之甚少,但我们几乎知道H(X)的一切:它的公式,参数等。关于 H(X),我们唯一不知道的是它的参数值。
事实上,机器学习的主要关注点是找到为给定问题和数据确定合适参数值的方法。让我们看看我们如何执行它。
在机器学习术语中,H(X)被称为“F(X)的近似值”。H(X)的存在被通用近似定理所涵盖。
五、成本函数和通用逼近定理
考虑这样一种情况:我们知道输入的值和相应的输出,但我们不知道 的公式。例如,我们知道如果输入是,那么结果就是。XY = F(X)F(X)X = 1.0F(1.0)Y = 2.0
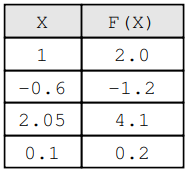
4 X 和 F(X) 的映射
现在,考虑我们有一个已知的函数,我们想知道是否是 的良好近似。因此,我们计算并找到.H(X)H(X)F(X)T = H(1.0)T = 1.9
这个值有多糟糕,因为我们知道真正的值是什么时候?T = 1.9Y = 2.0X = 1.0
用于量化 和 之间的差额的成本的指标由成本函数调用。YT
请注意,Y 是期望值,T 是我们猜测获得的实际值
H(X)
成本函数的概念是机器学习的核心。让我们以最常见的成本函数为例。
六、均方误差
最著名的成本函数是均方误差:
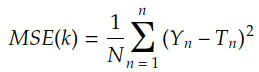
其中 Ti 由核 k 对 Xi 的卷积给出:
![]()
我们在上一个故事中讨论了卷积
请注意,我们有 n 对 (Yn, T n),每对都是期望值 Yi 和实际值 Tn 的组合。例如:
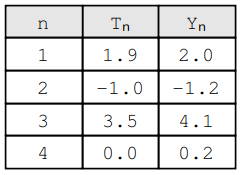
因此,MSE 的评估如下:
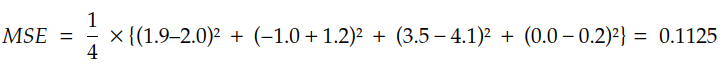
我们可以编写MSE的第一个版本,如下所示:
auto MSE = [](const std::vector<double> &Y_true, const std::vector<double> &Y_pred) {
if (Y_true.empty()) throw std::invalid_argument("Y_true cannot be empty.");
if (Y_true.size() != Y_pred.size()) throw std::invalid_argument("Y_true and Y_pred sizes do not match.");
auto quadratic = [](const double a, const double b) {
double result = a - b;
return result * result;
};
const int N = Y_true.size();
double acc = std::inner_product(Y_true.begin(), Y_true.end(), Y_pred.begin(), 0.0, std::plus<>(), quadratic);
double result = acc / N;
return result;
};现在我们知道了如何计算MSE,让我们看看如何使用它来近似函数。
七、使用MSE找到最佳参数的直觉
假设我们有一个映射 F(X) 合成生成:
F(X) = 2*X + N(0, 0.1)其中 N(0, 0.1) 表示从正态分布中抽取的随机值,平均值 = 0,标准差 = 0.1。我们可以通过以下方式生成示例数据:
#include <random>
std::default_random_engine dre(time(0));
std::normal_distribution<double> gaussian_dist(0., 0.1);
std::uniform_real_distribution<double> uniform_dist(0., 1.);
std::vector<std::pair<double, double>> sample(90);
std::generate(sample.begin(), sample.end(), [&gaussian_dist, &uniform_dist]() {
double x = uniform_dist(dre);
double noise = gaussian_dist(dre);
double y = 2. * x + noise;
return std::make_pair(x, y);
});如果我们使用任何电子表格软件绘制此示例,我们会得到如下所示的内容:
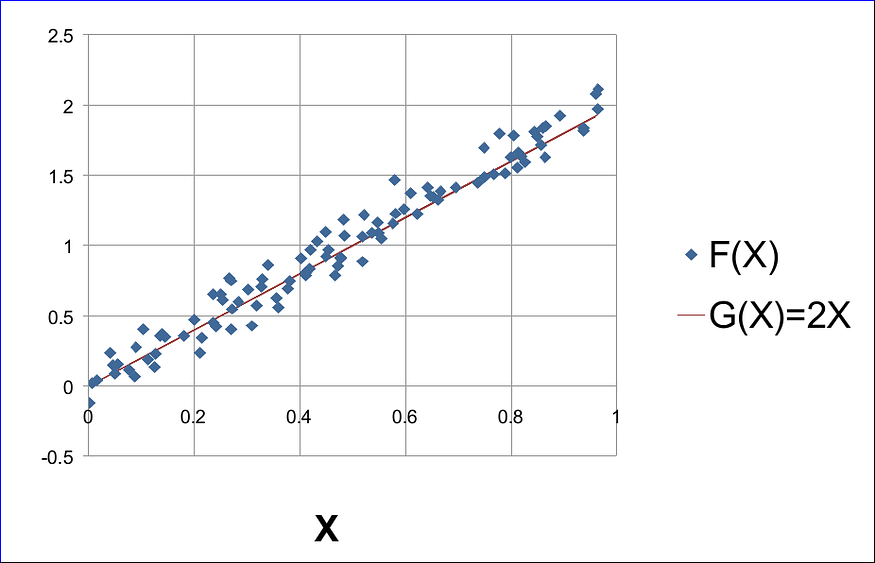
请注意,我们知道 G(X) 和 F(X) 的公式。然而,在现实生活中,这些生成器功能是潜在现象的未公开秘密。在这里,在我们的示例中,我们只知道它们,因为我们正在生成合成数据来帮助我们更好地理解。
在现实生活中,我们所知道的一切都是一个假设,即由H(X)= kX定义的假设函数H(X)可能是F(X)的良好近似值。 当然,我们还不知道k的值是多少。
让我们看看如何使用 MSE 找出合适的 k 值。事实上,它就像为一系列不同的 k 绘制 MSE 一样简单:
std::vector<std::pair<double, double>> measures;
double smallest_mse = 1'000'000'000.;
double best_k = -1;
double step = 0.1;
for (double k = 0.; k < 4.1; k += step) {
std::vector<double> ts(sample.size());
std::transform(sample.begin(), sample.end(), ts.begin(), [k](const auto &pair) {
return pair.first * k;
});
double mse = MSE(ys, ts);
if (mse < smallest_mse) {
smallest_mse = mse;
best_k = k;
}
measures.push_back(std::make_pair(k, mse));
}
std::cout << "best k was " << best_k << " for a MSE of " << smallest_mse << "\n";很多时候,这个程序输出的东西是这样的:
best k was 2.1 for a MSE of 0.00828671
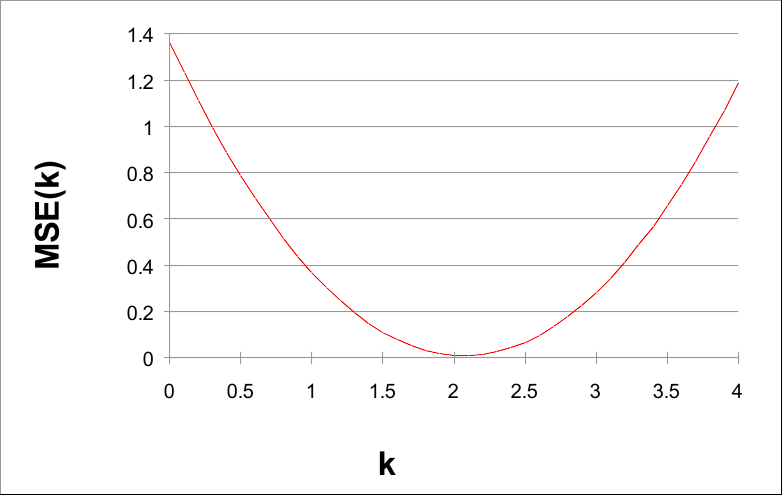
如果我们用k绘制MSE(k),我们可以看到一个非常有趣的事实:
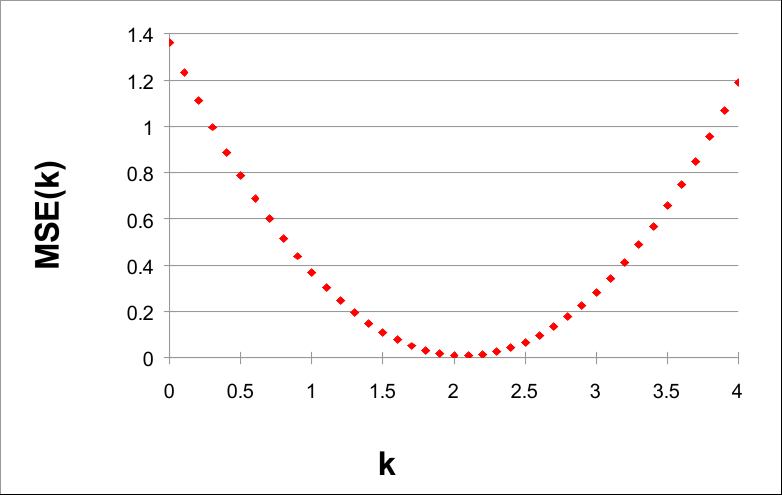
k 从 0 到 4,步长为 0.1
请注意,MSE(k) 的值在 k = 2 附近最小。实际上,2 是泛型函数 G(X) = 2X 的参数。
给定数据并使用 0.1 的步长,当 k = 2.1 时,可以找到较小的 MSE(k) 值。这表明 H(X) = 2.1 X 是 F(X) 的良好近似值。 事实上,如果我们绘制F(X)、G(X)和H(X),我们有:
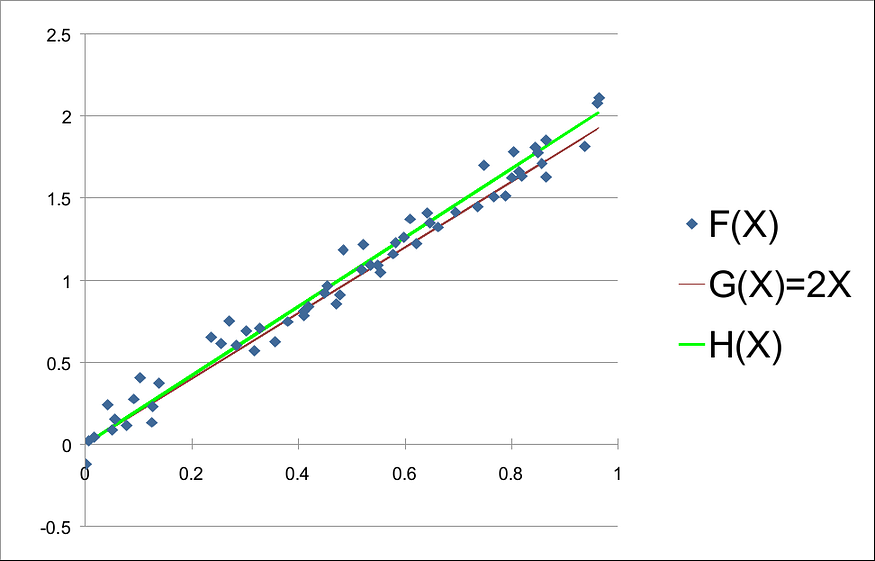
通过上面的图表,我们可以意识到H(X)实际上近似于F(X)。不过,我们可以尝试使用较小的步长(如 0.01 或 0.001)来找到更好的近似值。
代码可以在此存储库中找到
八、成本表面
MSE(k) 乘以 k 的曲线是成本曲面的一维示例。
前面的示例显示的是,我们可以使用成本表面的最小值来找到参数 k 的最佳拟合值。
该示例描述了机器学习中最重要的范式:通过成本函数最小化的函数近似。
上图显示了一个一维成本曲面,即给定一维k的成本曲线。在二维空间中,即当我们有两个k,即k1和k2时,成本面看起来更像一个实际曲面:
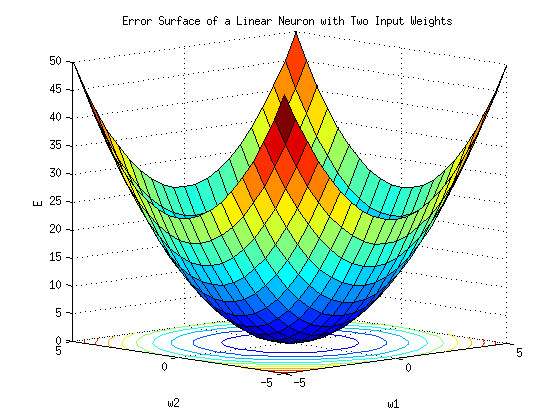
无论 k 是 1D、2D 还是更高维,找到最佳第 k 个值的过程都是相同的:找到成本曲线的最小值。
最小成本值也称为全局最小值。
在 1D 空间中,查找全局最小值的过程相对容易。然而,在高维度上,扫描所有空间以找到最小值可能会产生计算成本。在下一个故事中,我们将介绍大规模执行此搜索的算法。
不仅k可以是高维的。在实际问题中,输出通常也是高维的。让我们学习如何在这种情况下计算 MSE。
九、高维输出上的MSE
在现实世界的问题中,Y 和 T 是向量或矩阵。让我们看看如何处理这样的数据。
如果输出是一维的,则MSE的先前公式将起作用。但是如果输出是多维的,我们需要稍微改变一下公式。例如:
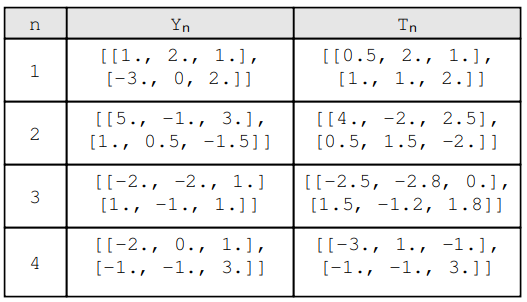
在这种情况下,Yn 和 Tn 不是标量值,而是大小矩阵。在将 MSE 应用于此数据之前,我们需要更改公式,如下所示:(2,3)

在此公式中,N 是对数,R 是行数,C 是每对中的列数。像往常一样,我们可以使用 lambda 实现此版本的 MSE:
#include <numeric>
#include <iostream>
#include <Eigen/Core>
using Eigen::MatrixXd;
int main()
{
auto MSE = [](const std::vector<MatrixXd> &Y_true, const std::vector<MatrixXd> &Y_pred)
{
if (Y_true.empty()) throw std::invalid_argument("Y_true cannot be empty.");
if (Y_true.size() != Y_pred.size()) throw std::invalid_argument("Y_true and Y_pred sizes do not match.");
const int N = Y_true.size();
const int R = Y_true[0].rows();
const int C = Y_true[0].cols();
auto quadratic = [](const MatrixXd a, const MatrixXd b)
{
MatrixXd result = a - b;
return result.cwiseProduct(result).sum();
};
double acc = std::inner_product(Y_true.begin(), Y_true.end(), Y_pred.begin(), 0.0, std::plus<>(), quadratic);
double result = acc / (N * R * C);
return result;
};
std::vector<MatrixXd> A(4, MatrixXd::Zero(2, 3));
A[0] << 1., 2., 1., -3., 0, 2.;
A[1] << 5., -1., 3., 1., 0.5, -1.5;
A[2] << -2., -2., 1., 1., -1., 1.;
A[3] << -2., 0., 1., -1., -1., 3.;
std::vector<MatrixXd> B(4, MatrixXd::Zero(2, 3));
B[0] << 0.5, 2., 1., 1., 1., 2.;
B[1] << 4., -2., 2.5, 0.5, 1.5, -2.;
B[2] << -2.5, -2.8, 0., 1.5, -1.2, 1.8;
B[3] << -3., 1., -1., -1., -1., 3.5;
std::cout << "MSE: " << MSE(A, B) << "\n";
return 0;
}
值得注意的是,无论 k 或 Y 是多维的还是不是多维的,MSE 始终是一个标量值。
十、其他成本函数
除了MSE,深度学习模型中也经常出现其他成本函数。最常见的是分类交叉熵、对数 cosh 和余弦相似性。
我们将在接下来的故事中介绍这些功能,特别是当我们介绍分类和非线性推理时。
十一、结论和下一步
成本函数是机器学习中最重要的主题之一。在这个故事中,我们学习了如何编写最常用的成本函数MSE代码,以及如何使用它来适应一维问题。我们还了解了为什么成本函数对于查找函数近似如此重要。
在下一个故事中,我们将学习如何使用成本函数从数据中训练卷积核。我们将介绍拟合内核的基本算法,并讨论训练机制的实现,例如 epoch、停止条件和超参数