BP算法之非线性函数的拟合

一、BP算法原理

BP算法由输入信号的正向传播和输出误差的反向传播两个过程组成。
正向传播：输入样本从输入层进入网络，经隐层逐层传递至输出层，如果输出层的实际输出与期望输出不同，则转至误差进行反向传播；如果输出层的实际输出与期望输出相同，则结束学习算法。
反向传播：将输出误差通过隐藏层反传至输入层，在反传过程中将误差分摊给各层的各个节点，获得各层各个节点的误差信号，并将其作为修正各节点权值的根据。这一计算过程使用梯度下降法完成，在不停地调整各层神经元的权值和阈值后，使误差信号减小到最低限度。
权值和阈值不断调整的过程，就是网络的学习与训练过程，经过信号的正向传播与误差的反向传播，权值和阈值反复进行调整，一直进行到预先设定的学习训练次数，或者输出误差减小到允许的程度。
链接：link

二、模型

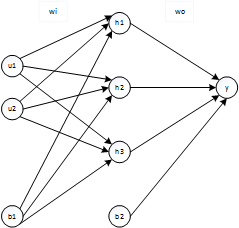
三、算法步骤

1.传统BP算法：

(1) 给定输入/输出样本对(u,y)
(2) 随机产生初始权重值$w_i,w_o,b_1,b_2$
(3) 计算输出值：

hi_in=w1*u+b;
hi_out=f(hi_in);//f为激活函数，自选，一般是sigmoid函数
y_in=w2*hi_out+b2;
y_out=g(y_in);//g为激活函数，自选，一般是sigmoid函数，如果拟合非线性函数，还可以是恒等函数

(4) 计算最大的误差百分比：$maxError=(y-y_{out})/y\ast 100$%。
(5) 判断maxError是否满足要求，满足要求则此次循环，不再更新权重（不再向下进行），否则继续。
注：这里有的地方可能会用到目标函数值是否符合要求，进而判断接下来的走向
(6) 目标函数选取：E=$\frac{1}{2}\times (y-y_{o}ut{)}^2$
(7) 利用梯度下降法更新权重：
增量：
$\delta w_o=\frac{\partial E}{\partial w_o}=\frac{\partial E}{\partial y_{out}}\frac{\partial y_{out}}{\partial y_{in}}\frac{\partial y_{in}}{\partial w_o}$

$\delta b_2=\frac{\partial E}{\partial b_2}=\frac{\partial E}{\partial y_{out}}\frac{\partial y_{out}}{\partial y_{in}}\frac{\partial y_{in}}{\partial b_2}$

$\delta w_i=\frac{\partial E}{\partial w_i}=\frac{\partial E}{\partial y_{out}}\frac{\partial y_{out}}{\partial y_{in}}\frac{\partial y_{in}}{\partial h_{out}}\frac{\partial h_{out}}{\partial h_{in}}\frac{\partial h_{in}}{\partial w_i}$

$\delta b_1=\frac{\partial E}{\partial b_1}=\frac{\partial E}{\partial y_{out}}\frac{\partial y_{out}}{\partial y_{in}}\frac{\partial y_{in}}{\partial h_{out}}\frac{\partial h_{out}}{\partial h_{in}}\frac{\partial h_{in}}{\partial b_1}$

注意：以上因为是单隐藏层，单输出，所以只需要求偏导就行，对于多输出的网络，或者多隐藏层的网络，中间求出来的是全导数。
更新：
$w_o=$$w_o-\eta \times \delta w_o,\eta$是学习率；
$b_2=$$w_i-\eta \times \delta b_2$;
$w_i=$$w_i-\eta \times \delta w_i$;
$b_1=$$b_1-\eta \times \delta b_1$;

2.传统算法的局限性

• 易形成局部极小而得不到全局最优
• 训练次数多使得学习效率低，收敛速度慢
• 隐含层节点的选取缺乏理论指导
• 训练时学习新样本有遗忘旧样本的趋势

3.BP算法的改进

• 增加动量项
• 自适应调节学习率
• 引入陡度因子
  (1)增加动量项
  标准BP算法只按t时刻误差的梯度降方向调整，而没有考虑t时刻以前的梯度方向，从而常使训练过程发生振荡，收敛缓慢。
  解决办法是在权值的调整公式中增加一个动量项：$\alpha \times \delta w(t-1),0<\alpha <1$。
  动量项的实质是从前一次权值调整量中取出一部分迭加到本次权值调整量中。它反映了以前积累的调整经验，对于t 时刻的调整起阻尼作用。当误差曲面出现骤然起伏时，可减小振荡趋势，提高训练速度。
  (2)自适应调节学习率
  标准BP算法中，学习率$\eta$ 确定一个从始至终都合适的最佳学习率很难。平坦区域内，$\eta$ 太小会使训练次数增加；在误差变化剧烈的区域，$\eta$ 太大会因调整量过大而跨过较窄的“坑凹”处，使训练出现振荡，反而使迭代次数增加。
  解决办法是根据环境的变化，自动调整学习率$\eta$。
  设一初始学习率，若经过一批次权值调整后，总误差增大，则本次调整无效，令$\eta =\beta \times \eta ,\beta <1$；若经过一批次权值调整后，总误差下降，则本次调整有效，令$\eta =\theta \times \eta ,\theta >1$。
  (3)引入陡度因子
  此方法针对于不同的激活函数有不同的方法，对于sigmoid函数：
  误差曲面上存在着平坦区域，权值调整进入平坦区的原因是输出层的输出值进入了激活函数的饱和区。
  如果在调整进入平坦区后，设法压缩输出层的净输入，使其输出退出激活函数的饱和区，就可以改变误差函数的形状，从而脱离平坦区。
  在激活函数中引入一个陡度因子$\lambda =1$，使得$y=\frac{1}{1+e^{-\frac{x}{\lambda }}}$。
  当发现目标函数的变化较小，而误差仍然比较大时，可以判断出此时已经进入了平坦区，修改$\lambda$，使$\lambda >1$。当退出平坦区后，再令$\lambda =1$。
  $\lambda$>1 ：净输入坐标压缩了$\lambda$倍，激活函数曲线的敏感区段变长，从而可使绝对值较大的净输入退出饱和值。
  $\lambda$：激活函数恢复原状，对绝对值较小的净输入具有较高的灵敏度。

四、注意事项

• 编程时，输入输出数据要先进行归一化处理，因为最后输出层的激活函数的值域与期望值可能不一致。
• 权重的改变是利用一组输入中的全部，不能输入一个数据改变一次权重
• 训练集曲线可能看着与期望的曲线不一致，但是并不代表训练是无效的，有时看到的未必就是真的，测试集的输出可能是满足要求的，要验证后才能知道此次训练是否合理正确。

五、matlab代码

%训练数据集
row = 1;
for i=0:0.01:1
   for j=0:0.01:1
   u(1,row) = i;
   u(2,row) = j;
   ytrue(1,row) = sin(u(1,row))/2+sin(u(2,row))/2;
   row = row+1;
   end
end
row=row-1;

%测试数据集
t_row=1;
for i=1:0.01:1.1
   for j=1:0.01:1.1
   test_u(1,t_row) = i;
   test_u(2,t_row) = j;
   testValue(1,t_row) = sin(test_u(1,t_row))/2+sin(test_u(2,t_row))/2;
   t_row = t_row+1;
   end
end
t_row=t_row-1;

%网络结构
inputnum = 2;     %输入层节点数
hiddennum = 9;    %隐含层节点数
outputnum = 1;    %输出层节点数

%循环次数
count=1000;

%参数
alpha=0.95;%动量因子
beta=0.8;%自适应学习率调整因子
theta=1.2;%自适应学习率调整因子
lambda=1;%陡度因子
yita=0.0005;%学习率

%定义训练集变量
hidein=zeros(hiddennum,row);
hideout=zeros(hiddennum,row);
yin=zeros(1,row);
yout=zeros(1,row);

%定义测试集变量
testError=zeros(1,t_row);
testHidein=zeros(hiddennum,t_row);
testHideout=zeros(hiddennum,t_row);
testOut=zeros(1,t_row);

%初始化权重值
wi1=0.2*rand(hiddennum,1)-0.1;
wi2=0.2*rand(hiddennum,1)-0.1;
bi=0.2*rand(hiddennum,1)-0.1;
wo=0.2*rand(hiddennum,1)-0.1;
bo=0.2*rand-0.1;

%定义权重增量
dwi1Last=zeros(hiddennum,1);
dwi2Last=zeros(hiddennum,1);
dbiLast=zeros(hiddennum,1);
dwoLast=zeros(hiddennum,1);
dboLast=zeros(1,1);

%中间变量
perror=zeros(1,row);
pdwi1=zeros(hiddennum,row);
pdwi2=zeros(hiddennum,row);
pdbi=zeros(hiddennum,row);
pdwo=zeros(hiddennum,row);
pdbo=zeros(1,row);

%目标函数
pobjfunc=zeros(1,row);
objfuncLast=0;

for i=1:count    
    dwi1=zeros(hiddennum,1);
    dwi2=zeros(hiddennum,1);
    dbi=zeros(hiddennum,1);
    dwo=zeros(hiddennum,1);
    dbo=zeros(1,1);
    objfunc=0;
    sumAbsError=0;
    
    %求输出和各个输入引起的增量
    for j=1:row
        hidein(:,j)=wi1*u(1,j)+wi2*u(2,j)+bi;
        hideout(:,j)=sigmoid(hidein(:,j),lambda);
        yin(j)=hideout(:,j)'*wo+bo;
        
        yout(j)=yin(j);
%         yout(j)=sigmoid(yin(j),lambda);
        
        perror(j)=ytrue(j)-yout(j);
        pobjfunc(j)=0.5*perror(j)*perror(j);
        
        pdwo(:,j)=perror(j)*hideout(:,j);
        pdbo(j)=perror(j);
%         pdwo(:,j)=perror(j)*yout(j)*(1-yout(j))*hideout(:,j);
%         pdbo(j)=perror(j)*yout(j)*(1-yout(j));
        
        pdwi1(:,j)=perror(j)*wo.*hideout(:,j).*(1-hideout(:,j))*u(1,j);%perror(j)*yout(j)*(1-yout(j))*wo.*hideout(:,j).*(1-hideout(:,j))*u(1,j);
        pdwi2(:,j)=perror(j)*wo.*hideout(:,j).*(1-hideout(:,j))*u(2,j);%perror(j)*yout(j)*(1-yout(j))*wo.*hideout(:,j).*(1-hideout(:,j))*u(2,j);
        pdbi(:,j)=perror(j)*wo.*hideout(:,j).*(1-hideout(:,j)); %perror(j)*yout(j)*(1-yout(j))*wo.*hideout(:,j).*(1-hideout(:,j)); 
%         pdwi1(:,j)=perror(j)*yout(j)*(1-yout(j))*wo.*hideout(:,j).*(1-hideout(:,j))*u(1,j);
%         pdwi2(:,j)=perror(j)*yout(j)*(1-yout(j))*wo.*hideout(:,j).*(1-hideout(:,j))*u(2,j);
%         pdbi(:,j)=perror(j)*yout(j)*(1-yout(j))*wo.*hideout(:,j).*(1-hideout(:,j)); 
    end
    
    %求各个输入产生的增量之和
    for j=1:row
       dwo=dwo+pdwo(:,j);
       dbo=dbo+pdbo(j);
       dwi1=dwi1+pdwi1(:,j);
       dwi2=dwi2+pdwi2(:,j);
       dbi=dbi+pdbi(:,j);
       objfunc=objfunc+pobjfunc(j);
       sumAbsError=sumAbsError+abs(perror(j));
    end
    
    %求增量均值
    dwo=dwo/row;
    dbo=dbo/row;
    dwi1=dwi1/row;
    dwi2=dwi2/row;
    dbi=dbi/row;
    
    %修改陡度因子
    if(abs(objfunc-objfuncLast)<0.01 && sumAbsError/row>0.5)
        lambda=1.2;
    else
        lambda=1;
    end
    
    %修改学习率
    if(i>5)
        if(objfuncLast/row<objfunc/row)
            yita=beta*yita;
        else
            yita=theta*yita;
        end
    end
    objfuncLast=objfunc;

    %修改权重
    wi1=wi1+(yita*dwi1+alpha*dwi1Last);
    dwi1Last=dwi1;
    wi2=wi2+(yita*dwi2+alpha*dwi2Last);
    dwi2Last=dwi2;
    bi=bi+(yita*dbi+alpha*dbiLast);
    dbiLast=dbi;
    wo=wo+(yita*dwo+alpha*dwoLast);
    dwoLast=dwo;
    bo=bo+(yita*dbo+alpha*dboLast);
    dboLast=dbo;
    
    %测试集
    maxTestError=0;
    for m=1:t_row
        testHidein(:,m)=wi1*test_u(1,m)+wi2*test_u(2,m)+bi;
        testHideout(:,m)=sigmoid(testHidein(:,m),1);
        testOut(m)=testHideout(:,m)'*wo+bo;
        testError(m)=(testValue(m)-testOut(m))/testValue(m);
        if(maxTestError<abs(testError(m)))
            maxTestError=abs(testError(m));
        end
    end
    if(maxTestError<0.05)
        break;
    end
    
end

%训练集函数输出
[x,y] = meshgrid(0:0.1:1,0:0.1:1);
trainFunctionOutput =sin(x)/2+sin(y)/2;
figure(1)
mesh(x,y,trainFunctionOutput)
xlabel('x');
ylabel('y');
zlabel('trainFunctionOutput');

%训练集实际输出
t1=linspace(min(u(1,:)),max(u(1,:)),10);
t2=linspace(min(u(2,:)),max(u(2,:)),10);
[X,Y]=meshgrid(t1,t2);
trainOutput=griddata(u(1,:),u(2,:),yout,X,Y);
figure(2)
mesh(X,Y,trainOutput)
xlabel('Input1');
ylabel('Input2');
zlabel('trainOutput');

%测试集函数输出
[tx,ty] = meshgrid(1:0.01:1.1,1:0.01:1.1);
testTunctionOutput =sin(tx)/2+sin(ty)/2;
figure(3)
mesh(tx,ty,testTunctionOutput)
xlabel('x');
ylabel('y');
zlabel('testTunctionOutput');

%测试集实际输出
t3=linspace(min(test_u(1,:)),max(test_u(1,:)));
t4=linspace(min(test_u(2,:)),max(test_u(2,:)));
[tX,tY]=meshgrid(t3,t4);
testOutput=griddata(test_u(1,:),test_u(2,:),testOut,tX,tY);
figure(4)
mesh(tX,tY,testOutput)
xlabel('Input1');
ylabel('Input2');
zlabel('testOutput');

%绘制误差曲线
t5=linspace(min(test_u(1,:)),max(test_u(1,:)));
t6=linspace(min(test_u(2,:)),max(test_u(2,:)));
[X1,X2]=meshgrid(t5,t6);
E=griddata(test_u(1,:),test_u(2,:),testError,X1,X2);
figure(5)
mesh(X1,X2,E)
xlabel('Input1');
ylabel('Input2');
zlabel('error');