T-PAMI2023: PAGCP-基于性能感知近似的多任务模型全局通道剪枝

概要

本文提出一个用于多任务CNN模型全局通道剪枝(global channel pruning)的框架PAGCP。作者从全局剪枝的角度出发，将模型压缩问题建模为联合通道显著性指标优化问题。该问题同时考虑了层间和层内通道对多任务模型压缩性能的联合影响作用。并通过对该问题的分析得到近似优化目标，由此提出基于性能感知准则(performance-aware oracle criterion)的序贯贪婪剪枝算法(sequentially greedy channel pruning)。该算法能够在不施加正则惩罚项的情况下高效确定多任务模型中存在的全局冗余通道，并实现压缩损失可控的效果。为了实现高效的性能压缩方式，作者表示所提的剪枝压缩框架具有以下优点：

在不需要正则约束训练的情况下实现对已训练模型的各层通道进行联合全局通道剪枝，压缩效果比施加了正则约束的压缩方式更好，同时减少了额外的训练开销
在最大化模型压缩比例的情况下实现对多任务模型的压缩损失可控，解决了传统敏感度分析和全局阈值设定在多任务模型下对压缩性能不可控的问题
广泛适用于多种下游任务和多种模型结构中，包括单阶段和双阶段的目标检测模型，密集预测的多任务模型，以及分类任务等，在端侧设备中实现性能略有下降的情况下最高3.3倍的加速效果

作者将PAGCP算法框架应用于SSD, FasterRCNN, CenterNet, YOLOv5, MTI-Net等多任务模型，并在PASCAL VOC, COCO, NYUD_V2, PASCAL Context等多个基准数据集上进行实验。实验表明在将多个模型FLOPs或参数量压缩比例超过60%的情况下，仅有略微的性能损失，超越了同等计算规模和模型结构下的现有高性能模型，同时大幅提升原模型推理速度。例如在PASCAL VOC上，YOLOv5m在压缩78%的参数量和65%FLOPs后仍保持81.7%mAP的性能，较原模型仅损失1.5%mAP；在COCO上，YOLOv5m在压缩71%的参数量和61%FLOPs后仍保持41.0%mmAP，较原模型仅损失2.6%mmAP。

论文信息

在这里插入图片描述

论文题目：Performance-aware Approximation of Global Channel Pruning for Multitask CNNs
发表单位：复旦大学，上海人工智能实验室
论文地址：https://arxiv.org/pdf/2303.11923.pdf
代码地址: https://github.com/HankYe/PAGCP

动机

在CNN模型剪枝算法中，大多数的有效性验证是基于简单的分类任务进行实验的，但实际模型落地时，往往需要对多任务(Multi-Task Learning, MTL)模型进行压缩部署。由于MTL模型本身首要关注的是提高多个任务推理的效率，所以在多任务模型上应用剪枝算法对于实现边缘设备、实时系统等的模型部署非常重要。然而，多任务模型剪枝比单任务模型（如分类模型）更具挑战性，因为多任务模型中的卷积核通常需要学习能够同时用于多个任务的特征表示，这导致不同层中的卷积核呈现出更强的的关联性和交互作用，即剪枝某个卷积核会影响其它卷积核对多任务模型的贡献。

举例而言，当其它卷积核被修剪后，任意一个卷积核关于各个任务的敏感度排名（即删除该卷积核引起的每个任务的性能下降排序）都可能会发生变化。再者，任意一个卷积核的注意力区域可能会在对其它卷积核进行剪枝后发生变化，从而导致了对各任务的性能贡献发生变化。图1展示了同一卷积核的注意力图中的高响应区域可能会受到其他卷积核修剪的显著影响。

在这里插入图片描述图1 在剪枝过程中卷积核的注意力区域因其它卷积核被剪枝而发生改变。(a)为注意力区域减少，(b), (c), (d)为注意力区域增多的情况。

总而言之，在多任务模型剪枝过程中，处于动态变化状态的卷积核重要程度（即显著性程度）会导致模型在压缩时很难找到模型的推理性能和压缩率之间的平衡点。这一问题和挑战在过去的单任务模型上的主流全局剪枝过程中很少被考虑到。主要原因为：在单任务模型中（以分类任务为例），特征的冗余度较高，如背景特征和低水平(low-level)特征等特征对物体分类预测的作用有限，因此剪枝过程中卷积核重要程度的变化对压缩性能的影响较小，在对冗余卷积核的重要程度评估存在误差时仍有大量相似的特征对模型进行弥补。

过去的多任务模型剪枝算法主要集中在模型迁移（将剪枝后的分类模型嵌入多任务模型框架下进行微调）或算法迁移（将分类模型的剪枝算法迁移到多任务模型压缩中），这两种迁移方式一方面忽略了上述所分析的卷积核之间的联合影响，另一方面忽略了任务之间的特征不匹配问题（多任务模型所需的特征较单任务模型所需的特征空间不匹配）。

基于上述分析，本文深入思考多任务模型的剪枝目标，并提出一个符合多任务模型特点的统一剪枝框架PAGCP。相比过去多任务模型压缩算法，PAGCP能仅利用剪枝技术直接在下游多任务模型上实现高压缩比和高性能的平衡。

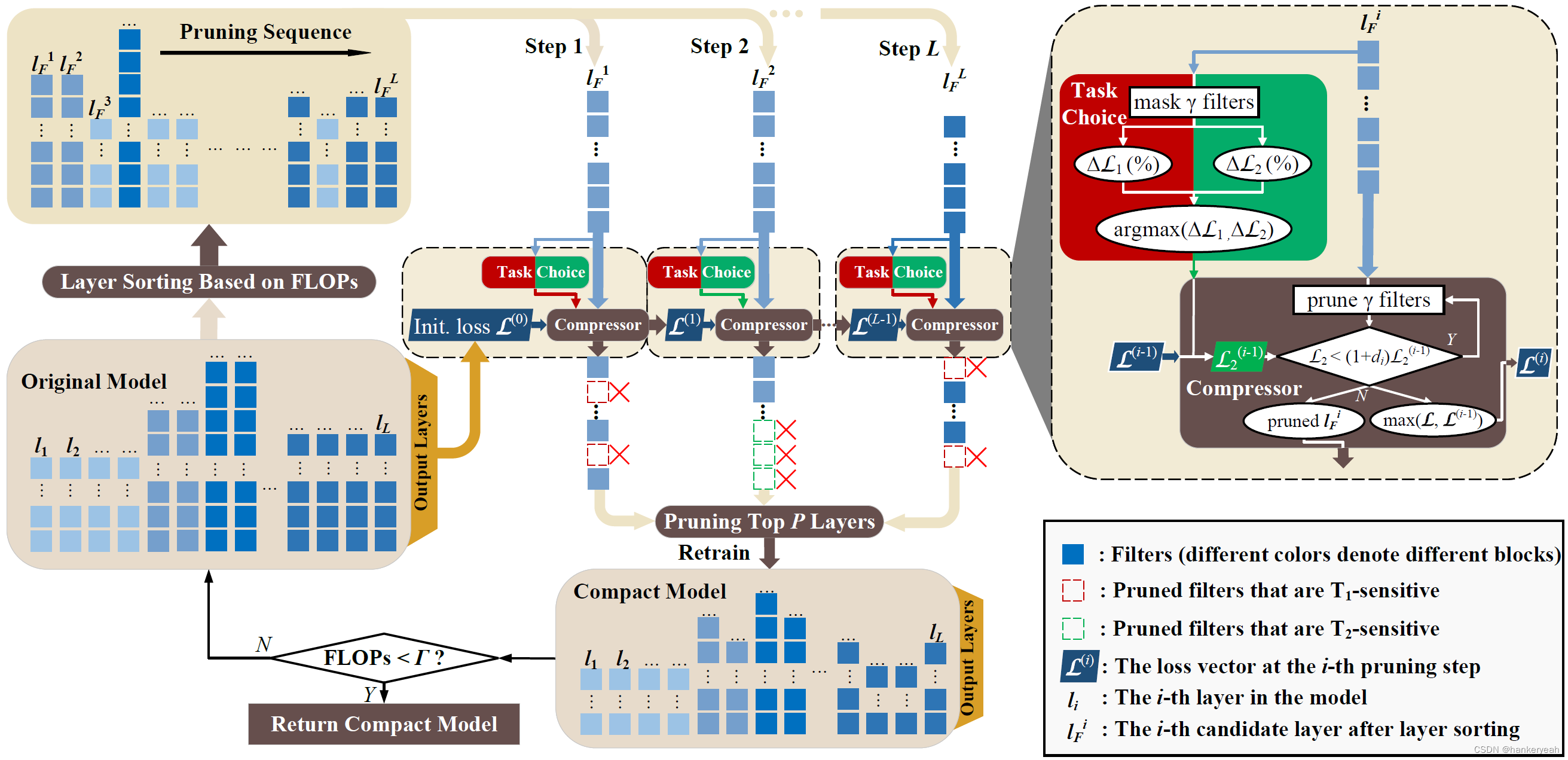
在这里插入图片描述

图2 PAGCP框架图。

PAGCP框架如图2所示，工程实现上的核心设计如下：

将模型各层剪枝的顺序设计为根据各层对模型的FLOPs贡献进行升序或降序排列，每个step从重排的层中选取层进行层内的通道剪枝。该重排的想法为后续实施基于联合通道显著性优化的压缩准则做铺垫。
在每个step的层内剪枝过程中引入上一个step的模型剪枝后结构以及上一个step中剪枝后的多任务loss状态向量（向量的每个元素为loss中的每一项），在该状态的基础上对当前层的压缩实现任务敏感性可知且模型性能可控的通道剪枝。
在确定所有layer的压缩比例后，重新评估每一层在所设定的压缩比例下对FLOPs的压缩贡献，选择贡献最大的若干层进行最终的剪枝，从而保留了那些压缩效果不明显却对模型性能存在损害的层来找到模型压缩比和模型性能之间更好的平衡点。

PAGCP框架适用于多种任务场景以及多种模型结构。在论文中，作者展示了将其应用于高压缩比和高性能情况下的有效性。另外，作者也展示了该框架应用于简单的分类模型压缩（可视为多任务的特例）的有效性，如在ImageNet上实现了对ResNet50进行60%+的FLOPs压缩率下仅降低0.14%Top-1 Acc.性能。

方法

本文目标是通过研究任意多个不同的卷积核之间的联合重要度来实现更优的全局剪枝策略。作者从基于显著性指标（也称重要性指标）的剪枝优化问题切入，分析得出传统引入正则惩罚项的方式中存在梯度竞争的问题，从而在优化中使得模型参数偏离了原本的最优点，改变了原始最优点上每个通道的重要程度。基于此问题，作者提出将剪枝优化目标调整为：

$\min_{\boldsymbol{\theta }\in \varOmega} \,\,\mathbb{E}_{x\sim D_x}\left[ \mathcal{S}\left( x; \boldsymbol{\theta}\right) \right] \,\,\text{s.t. }\boldsymbol{g}\left( \boldsymbol{\theta } \right) \leqslant \boldsymbol{\alpha}.$

具体而言，作者将优化目标调整为仅对显著性指标进行带约束最小化搜索，保持模型参数权重不变。其中约束项调整为对模型剪枝后的性能损失约束以及计算量约束。这保证了模型参数处于最优点并有更准确的重要度评估。

理论分析

一般而言，对于任意一个卷积核（以第 $l$ 层，第 $k$ 个卷积核为例，其二元掩膜记为 $\theta_{lk}$ ， $\theta_{lk}=0$ 表示删除该卷积核，反之则保留），其显著性指标 $\mathcal{}$ $\mathcal{S}(x;\theta_{lk})$ 可以通过下式表示：

$\begin{aligned} \mathcal{S}\left(x;\theta_{lk}\right) &= \lVert \boldsymbol{f}\left( x; \theta _{lk}\right) -\boldsymbol{f}\left( x;\theta _{lk}=0\right) \rVert _r\\ &\triangleq\mathcal{S}_{l}^{k}\left(x \right), \end{aligned}$

其中，其中 $\boldsymbol{f}(\cdot): \mathbb{R}^m\longrightarrow\mathbb{R}^n$ 是一个模型的预定义状态函数，如模型预测损失[1]或下一层激活映射的输出[2]。 $m, n$ 分别表示输入 $x$ 、状态 $\boldsymbol{f}$ 的维度， $r$ 为范数阶数。该显著性指标的定义在欧氏空间下衡量两个高维状态之间的距离，通过状态的变化剧烈程度表示该卷积核在输入为 $x$ 时的重要程度。

类似地，任意两个卷积核（以第 $p$ 层，第 $u$ 个卷积核和第 $q$ 层，第 $v$ 个卷积核为例，其二元掩膜分别记为 $\theta_{pu}, \theta_{qv}$ $，\theta_{pu}, \theta_{qv}=0$ 表示同时剪枝两个卷积核），其显著性指标 $\mathcal{}$ $\mathcal{S}(x;\theta_{pu},\theta_{qv})$ 可以通过下式表示：

$\begin{aligned} \mathcal{S}\left(x;\theta_{pu},\theta_{qv} \right)&=\lVert \boldsymbol{f}(x; \theta _{pu}, \theta_{qv}) -\boldsymbol{f}( x;\theta _{pu}, \theta_{qv}=0) \rVert _r\\ &\triangleq \mathcal{S}_{pq}^{uv}\left(x \right), \end{aligned}$

其中 $\mathcal{S}\left(x;\theta_{pu},\theta_{qv}=1 \right)$ 定义为输入为 $x$ 时的联合显著性，记作 $\mathcal{S}_{pq}^{uv}\left(x \right)$ $,\mathcal{S}\left(x;\theta_{pu}=0,\theta_{qv}=1\right)$ 定义为 $\theta_{pu}$ 关于 $\theta_{qv}$ 的条件显著性，记作 $\mathcal{S}_{q}^{v}|_{p}^{u}\left( x \right)$ 。基于以上定义，可以得到下述性质：

定理一：对任意两个卷积核，若其显著性指标定义满足上述定义，则有下列不等式成立：

$\mathcal{S}_{pq}^{uv}\left( x \right) \leqslant \mathcal{S}_{p}^{u}\left( x \right) + \mathcal{S}_{q}^{v}|_{p}^{u}\left( x \right).$

等号成立当且仅当

$\begin{aligned}\boldsymbol{f}\in\varPhi _f=\{ \boldsymbol{f}&|\boldsymbol{f}\left( x;\theta _{pu}=0 \right)\\=&\mathrm{mid}\{ \boldsymbol{f}\left( x;\theta _{pu}=1 \right) , \boldsymbol{f}\left( x;\theta _{pu}=0 \right) ,\\&\boldsymbol{f}\left( x;\theta _{pu},\theta _{qv}=0 \right)\},\forall x\in D_x\}.\end{aligned}$

上述定理表明任意两个卷积核的联合重要度的上界为一个卷积核的独立重要度和另一个卷积核的条件重要度之和。这启发作者将原目标函数的优化问题简化为对上界的最小化问题。

事实上，定理一可以扩展至任意多卷积核的情况。设有 $N$ 个卷积核，则下式成立：

$\mathcal{S}_{l_1l_2...l_N}^{k_1k_2...k_N}\left( x \right) \leqslant \mathcal{S}_{l_1}^{k_1} \left( x \right) +\sum_{i=2}^N{\mathcal{S}_{l_i}^{k_i}|_{l_1...l_{i-1}}^{k_1...k_{i-1}}\left( x \right)}$

其中 $l_i \in \left\{1,2,..., L\right\}, k_i \in \{1,2,..., K_{l_i}\}$ 分别表示第 $i$ 个卷积核所在的层索引和通道索引。

基于上述定理，可将原目标优化问题转换为近似的上界最小化问题：

$\begin{aligned} \underset{\boldsymbol{\theta}}{\min}\,\, & \mathbb{E}_{x\sim D_x}\left[ \mathcal{S}_{l_1}^{k_1} \left( x \right) +\sum_{i=2}^N{\mathcal{S}_{l_i}^{k_i}|_{l_1...l_{i-1}}^{k_1...k_{i-1}}\left( x \right)} \right],\\ & \text{s.t.}\,\,\,\, \boldsymbol{g}\left( \boldsymbol{\theta } \right) \leqslant \boldsymbol{\alpha }.\end{aligned}$

该目标函数表明联合重要度的最小化可通过由独立重要度联合多个条件重要度组成的多目标最小化来近似。因此，作者考虑将其进行分步优化。为了实现分步优化，进一步将约束条件也通过分步约束来近似。下面介绍具体优化策略：

优化策略：序贯式贪婪剪枝

首先确定分步优化中每一步的优化目标如下（以第 $l$ 步为例）：

$\begin{aligned} \underset{\boldsymbol{\theta}_l}{\min}\,\, & \mathbb{E}_{x\sim D_x}\left[ \mathcal{S}_{l}^{k_1}\left( x;\boldsymbol{\theta} \right) + \sum_{i=2}^{K_l}{\mathcal{S}_{l}^{k_i}|_{l}^{k_1...k_{i-1}}\left( x;\boldsymbol{\theta} \right)} \right],\\ &\text{s.t.}\,\,\,\, \boldsymbol{g}\left( \boldsymbol{\theta}_l \right) \leqslant \boldsymbol{\alpha}_l,\end{aligned}$

其中 $\boldsymbol{\theta}_l, \boldsymbol{\alpha}_l$ 为第 $l$ 步优化中的局部待优化掩膜参数和约束边界。一种启发式的分步方式为将掩膜参数集合根据所在层的集合进行划分，每一步优化一个层内的掩膜参数，同时也将全局的约束边界根据层数划分为若干局部约束边界。在每一步的优化对象选择，即层选择时，以贪婪的方式根据约束边界的收缩趋势确定层的顺序。具体而言，对于局部约束边界范围逐渐减小的情况，优先选择对压缩贡献更大的层进行剪枝，即赋予压缩贡献大的层更松弛的约束边界，从而使得模型整体的压缩比例更高。

在确定分步方式后，需要对确定目标函数的具体形式，即显著性指标的具体形式。考虑到在每一步优化中，子优化问题可以同样细化为由层内卷积核的条件重要度组成的多步优化问题，而层内遍历每一个条件重要度组合将对子问题的优化带来巨大的搜索代价。因此，作者将显著性指标设计为形如关于卷积核权重 $\ell_1$ -norm的形式。据此，对于每个卷积核的重要度性质满足定理一，同时与层内卷积核的重要度保持独立，仅受其它层的卷积核剪枝状态影响。具体表达如下式所示：

$\begin{aligned} f(x;\theta_{l_{1}k_{1}},..., \theta_{l_{N}k_{N}}) &=\sum_{i=1}^{N}{\theta_{l_{i}k_{i}}}\lVert \boldsymbol{\omega}_{l_{i}k_{i}}(\theta_{l_{1}k_{1}}, ..., \theta_{l_{N}k_{N}}) \rVert_1; \\ \mathcal{S}_{l_1,..., l_N}^{k_1,..., k_N}(x) &= \sum_{i=1}^{N}\lVert \boldsymbol{\omega}_{l_{i}k_{i}}(\theta_{l_{1}k_{1}}, ..., \theta_{l_{N}k_{N}}) \rVert_1,\end{aligned}$

其中 $\boldsymbol{\omega}_{l_{i}k_{i}}(\theta_{l_{1}k_{1}}, ..., \theta_{l_{N}k_{N}})$ 表示在剪枝状态为 $(\theta_{l_{1}k_{1}}, ..., \theta_{l_{N}k_{N}})$ 时第 $l_{i}$ 层第 $k_i$ 个卷积核的权重。在该定义下，每一步子优化问题的形式可以简化为：

$\underset{\boldsymbol{\theta}_l}{\min}\,\,\sum_{i=1}^{K_l}{\mathcal{S}_{l}^{k_i}\left( \boldsymbol{\theta} \right)}\,\,\, \text{s.t.}\,\boldsymbol{g}\left( \boldsymbol{\theta}_l \right) \leqslant \boldsymbol{\alpha}_l.$

这使得子优化问题可以在线性时间内得到层内所有卷积核的联合重要度。

对于约束条件的逐层分解，作者针对多任务的特性对每一步的约束条件进行个性化设计。具体而言，作者提出不同卷积核提取出的特征应该对不同的任务体现出不同的重要程度。

以目标检测模型为例，大多数浅层的卷积核集中于提取更多对回归任务有利的空间和细节信息；而大多数深层的卷积核集中于提取更多对分类任务有利的语义和抽象信息。因此，大多数浅层卷积核对回归任务更鲁棒而对分类任务更敏感，而大多数深层卷积核对分类任务更鲁棒而对回归任务更敏感。

因此，在考虑每一层的性能约束时，应该将约束更多地集中在最敏感的任务上，即保证每一层最敏感的任务的性能损失经过多层叠加能够在约束边界内。具体而言，性能约束形式设计为：

$\begin{aligned} g(\boldsymbol{\theta}) &=\lVert \varDelta\mathcal{L} _1( \boldsymbol{\theta}) , \varDelta\mathcal{L} _2( \boldsymbol{\theta}) , ..., \varDelta\mathcal{L} _T( \boldsymbol{\theta}) \rVert _{\infty}\\ &=\underset{1\leqslant t\leqslant T}{\max}| \varDelta\mathcal{L} _t(\boldsymbol{\theta})|,\end{aligned}$

其中 $\varDelta\mathcal{L}_t(\boldsymbol{\theta})$ 表示第 $i$ 个任务在剪枝状态为 $\boldsymbol{\theta}$ 时的相对损失变化。

而逐层的约束边界设计为级联式变化形式：

$\prod_{i=1}^{L}\left(1+d_1\lambda^{i-1}\right) = \alpha\,$

其中 $d_1$ 表示初始层剪枝时的约束边界，即 $g(\boldsymbol{\theta})$ 阈值， $\lambda$ 为每一步优化的约束边界相对于上一步中的约束边界的缩放因子， $\alpha$ 为全局的约束边界。

至此，压缩的整体策略均已介绍完成，其算法优化过程如下图所示。

在这里插入图片描述

实验

实验设置

作者在两种多任务设置下进行实验：目标检测，以及密集预测的多任务模型。

数据集分别为：目标检测基准数据集（PASCAL VOC, COCO）, 密集预测基准数据集（NYUD_v2，PASCAL Context）。

压缩模型分别为：目标检测基线模型（SSD, FasterRCNN，CenterNet，YOLOv5），密集预测基线模型（MTI-Net）。

实验结果

这里仅展示主要压缩结果，更多实验结果及分析可查阅论文中的内容。

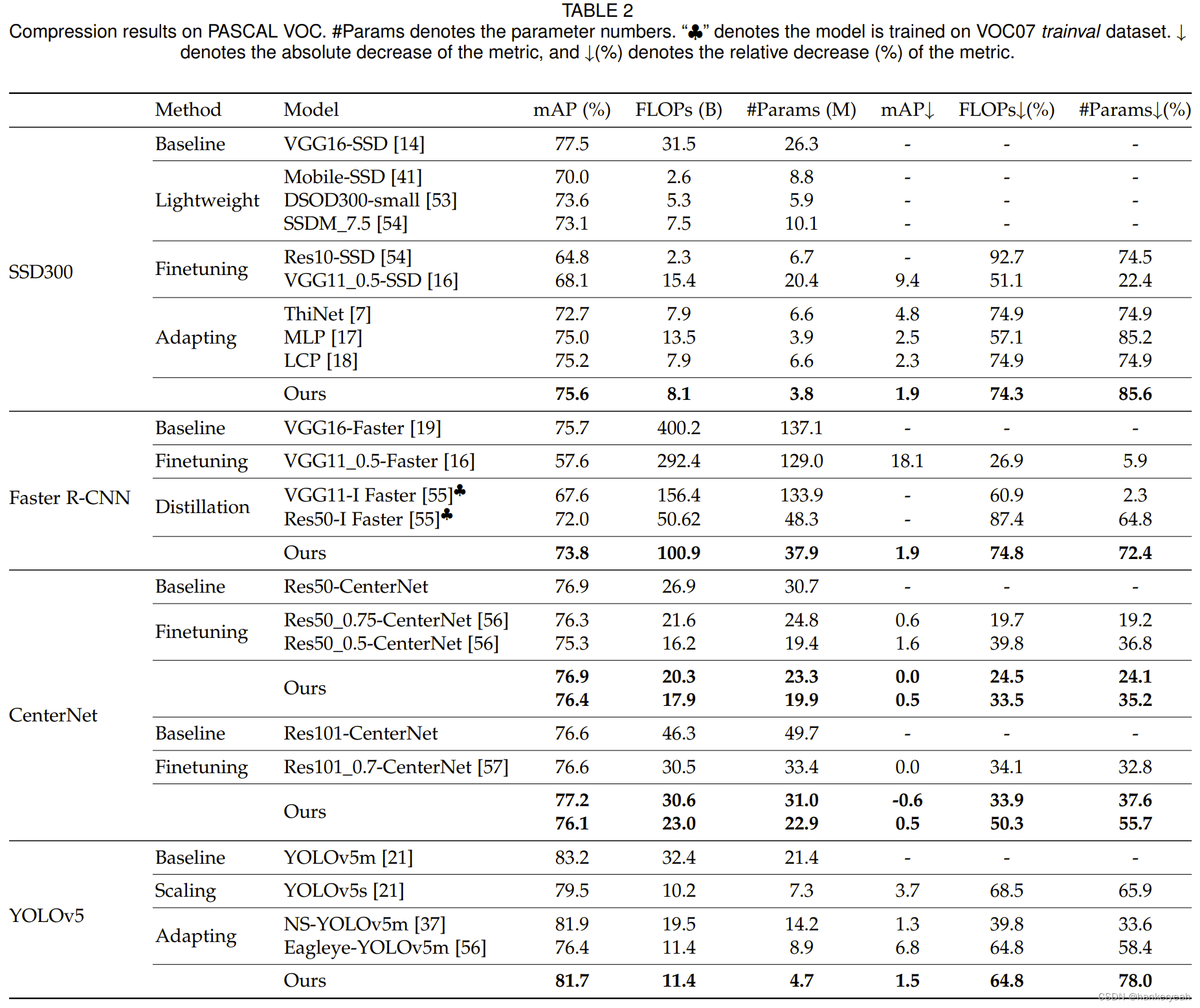
PASCAL VOC上的压缩结果比较：

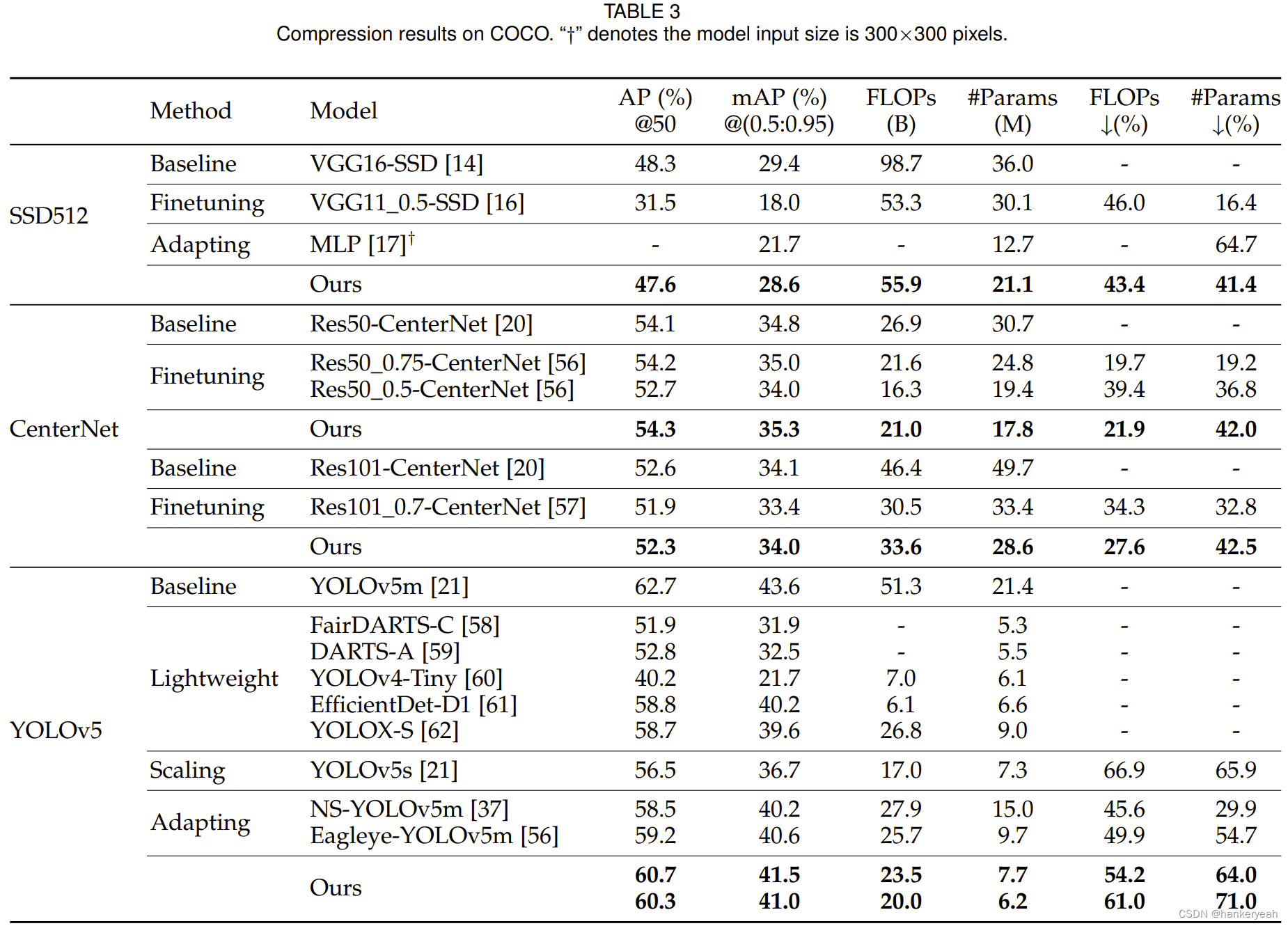
在这里插入图片描述

COCO上的压缩结果比较：

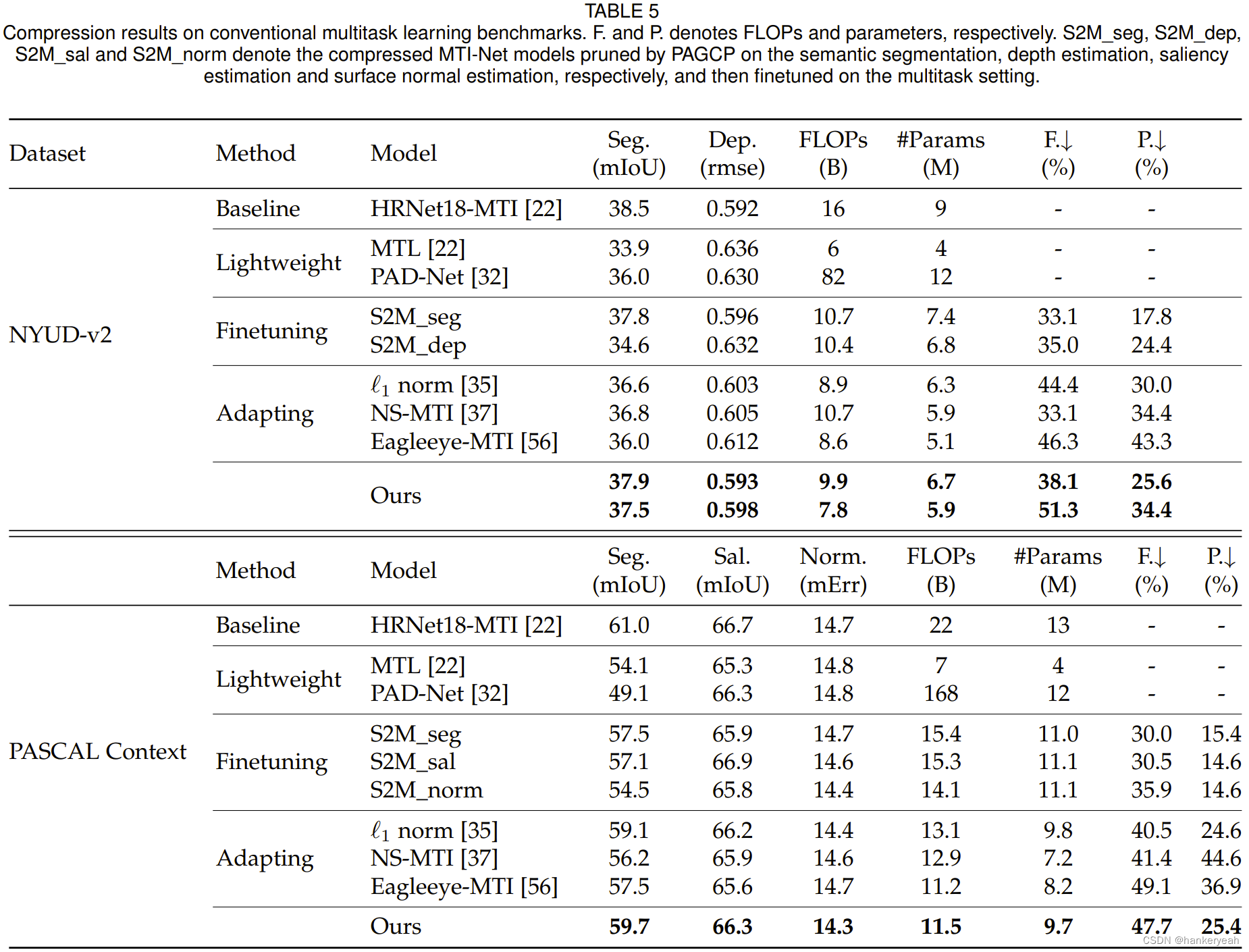
在这里插入图片描述

NYUD_v2和PASCAL Context上的压缩结果比较：

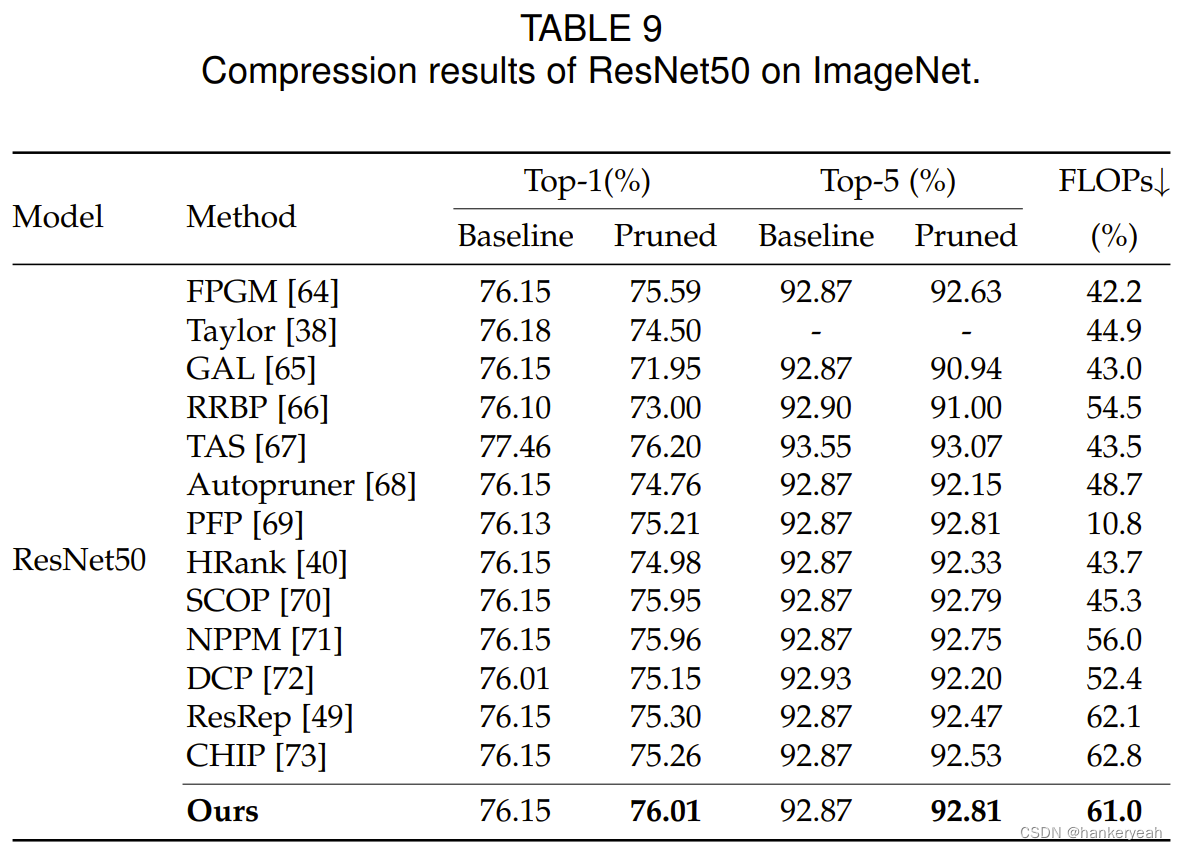
在这里插入图片描述

ImageNet上的压缩结果比较：

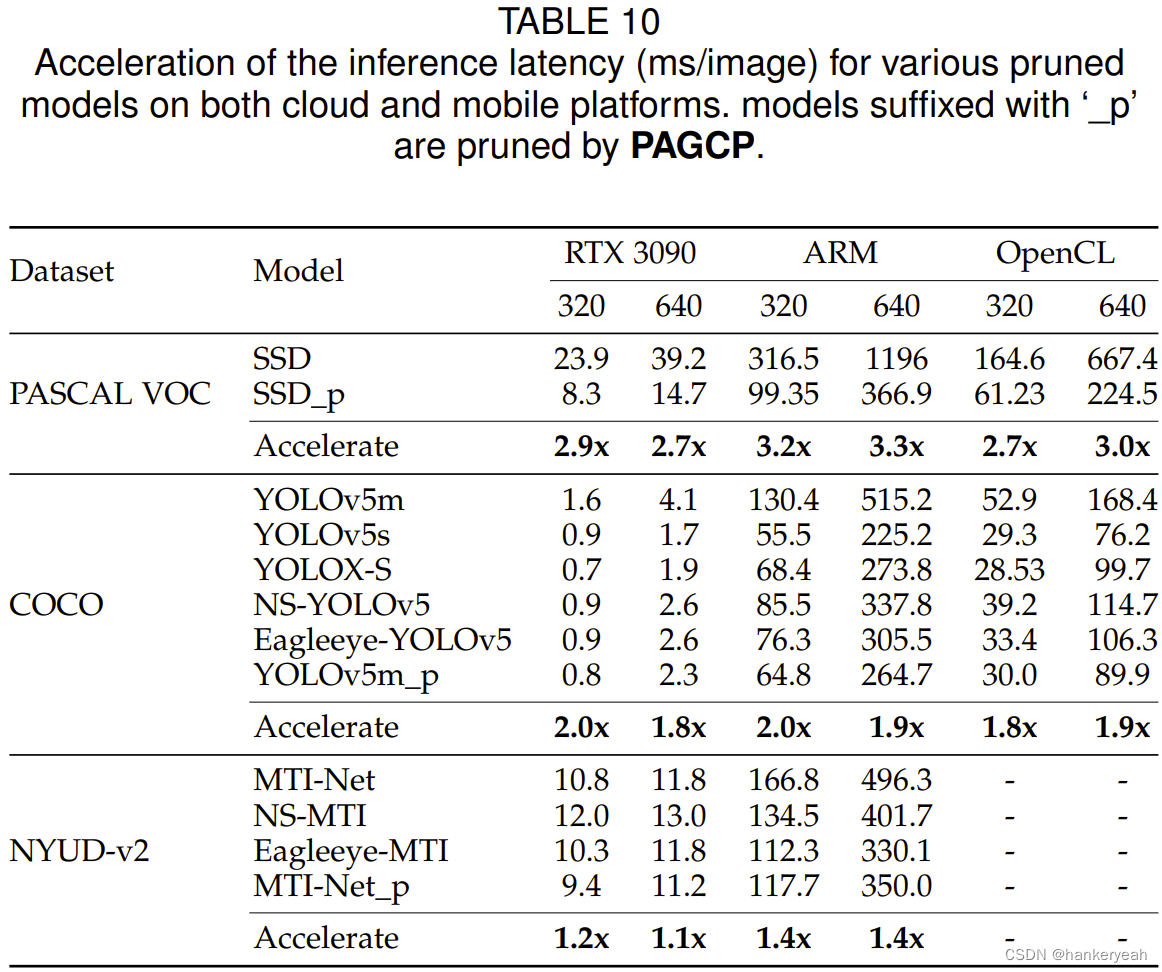
在这里插入图片描述

多平台上部署后的加速效果比较：

在这里插入图片描述

检测效果可视化：

在这里插入图片描述

多任务密集预测效果可视化

在这里插入图片描述

总结

本文提出了一种基于性能感知近似的全局通道剪枝框架（PAGCP），可以有效并广泛应用于包括目标检测、多任务密集预测甚至分类等各种模型的压缩中。作者从理论上推导出PAGCP的优化目标，并设计了序贯式贪心剪枝策略来近似解决目标问题。该剪枝策略通过分步的序贯式通道剪枝来考虑层内和层间不同卷积核对压缩性能的相互影响，并通过性能感知的Oracle约束准则来考虑卷积核对不同任务的敏感程度不同这一特性。作者在多个检测、MTL和分类数据集上进行的大量实验表明，所提出的PAGCP在预测准确度、参数量和FLOPs等方面可以实现最先进的压缩性能，并且可以很好地推广到各种单阶段和双阶段检测器、MTL模型和分类网络。同时作者还实验了压缩后模型的实际推理时间，在云计算和移动平台上展示了压缩后模型在移动设备上的实时性。