卡尔曼滤波原理（三）连续随机系统的离散化与连续时间Kalman滤波

实际建模中给的可能是连续的状态方程、连续的量测方程；要用Kalman滤波得先进行离散化。

一、连续时间系统方程离散化

1、连续时间模型

$$\dot{\mathbf{X}}(t)=\mathbf{F}(t)\mathbf{X}(t)+\mathbf{G}(t)\mathbf{w}(t)\mathrm{E}[\mathbf{w}(t)]=0,\mathrm{E}\left[\mathbf{w}(t){\mathbf{w}}^{\mathrm{T}}(\tau )\right]=\mathbf{q}(t)\delta (t-\tau )$$

连续时间的白噪声不太好理解，它处处连续，处处不可导，幅值无穷大，任何两个时间不相关，且是高斯白噪声

在 $t_{k-1}$ 到 $t_k$ 做积分，将 $t_{k-1}$ 到 $t_k$ 时间内连续的状态方程，转化为 $k-1$ 到 $k$ 两时刻间的状态方程，得到离散化形式：
$${\mathbf{X}}_k={\mathbf{\Phi }}_{k/k-1}{\mathbf{X}}_{k-1}+{\mathbf{\eta }}_{k-1}$$
其中：
$$\begin{array}{l}{\mathbf{X}}_k=\mathbf{X}\left(t_k\right)\\ {\mathbf{\Phi }}_{k/k-1}=\mathbf{\Phi }\left(t_k,t_{k-1}\right)\approx {\mathrm{e}}^{{\int }_{t_{k-1}}^{t_k}F(\tau )\mathrm{d}\tau }\\ {\mathbf{\eta }}_{k-1}={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{w}(\tau )\mathrm{d}\tau \end{array}$$

2、状态转移矩阵计算

泰勒展开之后取常数项和一阶项；舍弃后面计算量大且收益小的高阶项，得：
$${\mathbf{\Phi }}_{k/k-1}\approx {\mathrm{e}}^{F\left(t_{k-1}\right)T_s}=\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)T_s+{\mathbf{F}}^2\left(t_{k-1}\right)\frac{I_s^2}{\partial !}+{\mathbf{F}}^3\left(t_{k-1}\right)\frac{I_s}{\partial !}+\cdots \approx \mathbf{I}+\mathbf{F}\left(t_{k-1}\right)T_s$$

3、激励噪声的等效计算

$${\mathbf{\eta }}_{k-1}={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{w}(\tau )\mathrm{d}\tau$$
连续时间系统的噪声是高斯白噪声，经过线性变换（微积分也是线性变换），得到的还是高斯白噪声。想了解它，只要知道它的一阶矩和二阶矩就行了

激励噪声均值：
$$\mathrm{E}\left[{\mathbf{\eta }}_{k-1}\right]=\mathrm{E}\left[{\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{w}(\tau )\mathrm{d}\tau \right]={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathrm{E}[\mathbf{w}(\tau )]\mathrm{d}\tau =0$$
激励噪声协方差：
$$\mathrm{E}\left[{\mathbf{\eta }}_{k-1}{\mathbf{\eta }}_{j-1}^{\mathrm{T}}\right]=0k\ne j$$

$$\begin{array}{rl}\mathrm{E}\left[{\mathbf{\eta }}_{k-1}{\mathbf{\eta }}_{k-1}^{\mathrm{T}}\right]& =\mathrm{E}\left\{{\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{w}(\tau )\mathrm{d}\tau \cdot {\left[{\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,s\right)\mathbf{G}(s)\mathbf{w}(s)\mathrm{d}s\right]}^{\mathrm{T}}\right\}k=j\\ & =\mathrm{E}\left[{\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{w}(\tau ){\int }_{t_{k-1}}^{t_k}{\mathbf{w}}^{\mathrm{T}}(s){\mathbf{G}}^{\mathrm{T}}(s){\mathbf{\Phi }}^{\mathrm{T}}\left(t_k,s\right)\mathrm{d}s\mathrm{d}\tau \right]\\ & ={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau ){\int }_{t_{k-1}}^{t_k}\mathrm{E}\left[\mathbf{w}(\tau ){\mathbf{w}}^{\mathrm{T}}(s)\right]{\mathbf{G}}^{\mathrm{T}}(s){\mathbf{\Phi }}^{\mathrm{T}}\left(t_k,s\right)\mathrm{d}s\mathrm{d}\tau \\ & ={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau ){\int }_{t_{k-1}}^{t_k}\mathbf{q}(\tau )\delta (\tau -s){\mathbf{G}}^{\mathrm{T}}(s){\mathbf{\Phi }}^{\mathrm{T}}\left(t_k,s\right)\mathrm{d}s\mathrm{d}\tau \\ & ={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{q}(\tau ){\mathbf{G}}^{\mathrm{T}}(\tau ){\mathbf{\Phi }}^{\mathrm{T}}\left(t_k,\tau \right)\mathrm{d}\tau \end{array}$$

想往下算，得做一些假设，在 $t_{k-1}$ 到 $t_k$ 这一小段时间内，$\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )$ 都为常值，时不变；不是常值可以取一阶项
$$\begin{array}{rl}\mathrm{E}& \left[{\mathbf{\eta }}_{k-1}{\mathbf{\eta }}_{k-1}^{\mathrm{T}}\right]={\int }_{t_{k-1}}^{t_k}\mathbf{\Phi }\left(t_k,\tau \right)\mathbf{G}(\tau )\mathbf{q}(\tau ){\mathbf{G}}^{\mathrm{T}}(\tau ){\mathbf{\Phi }}^{\mathrm{T}}\left(t_k,\tau \right)\mathrm{d}\tau \\ \approx & {\int }_{t_{k-1}}^{t_k}\left[\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)\left(t_k-\tau \right)\right]\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right){\left[\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)\left(t_k-\tau \right)\right]}^{\mathrm{T}}\mathrm{d}\tau \\ =& {\int }_{t_{k-1}}^{t_k}\mathbf{G}\left(t_{k-1}\right)\mathbf{q}{\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)\mathrm{d}\tau +{\int }_{t_{k-1}}^{t_k}\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right){\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right)\left(t_k-\tau \right)\mathrm{d}\tau \\ & +{\int }_{t_{k-1}}^{t_k}\mathbf{F}\left(t_{k-1}\right)\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)\left(t_k-\tau \right)\mathrm{d}\tau +{\int }_{t_{k-1}}^{t_k}\mathbf{F}\left(t_{k-1}\right)\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right){\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right){\left(t_k-\tau \right)}^2\mathrm{d}\tau \\ =& \mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)T_s+\frac{1}{2}\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right){\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right)T_s^2\\ & +\frac{1}{2}\mathbf{F}\left(t_{k-1}\right)\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)T_s^2+\frac{1}{3}\mathbf{F}\left(t_{k-1}\right)\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right){\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right)T_s^3\\ =& \left[\mathbf{I}+\frac{1}{2}\mathbf{F}\left(t_{k-1}\right)T_s\right]\cdot \left[\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)T{T}_s\right]\cdot {\left[\mathbf{I}+\frac{1}{2}\mathbf{F}\left(t_{k-1}\right)T_s\right]}^{\mathrm{T}}+\frac{1}{12}\mathbf{F}\left(t_{k-1}\right)\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right){\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right)T_s^3\\ \approx & \left\{\left[\mathbf{I}+\frac{1}{2}\mathbf{F}\left(t_{k-1}\right)T_s\right]\mathbf{G}\left(t_{k-1}\right)\right\}\cdot \left[\mathbf{q}\left(t_{k-1}\right)T_s\right]\cdot {\left\{\left[\mathbf{I}+\frac{1}{2}\mathbf{F}\left(t_{k-1}\right)T_s\right]\mathbf{G}\left(t_{k-1}\right)\right\}}^{\mathrm{T}}\end{array}$$
如果时间极短，还可以再简化：
$$\mathrm{E}\left[{\mathbf{\eta }}_{k-1}{\mathbf{\eta }}_{k-1}^{\mathrm{T}}\right]\approx \mathbf{G}\left(t_{k-1}\right)\cdot \left[\mathbf{q}\left(t_{k-1}\right)T_s\right]\cdot {\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)\mathbf{F}\left(t_{k-1}\right)T_s\ll \mathbf{I}$$

4、最终离散化结论

扫描二维码关注公众号，回复： 15916605 查看本文章

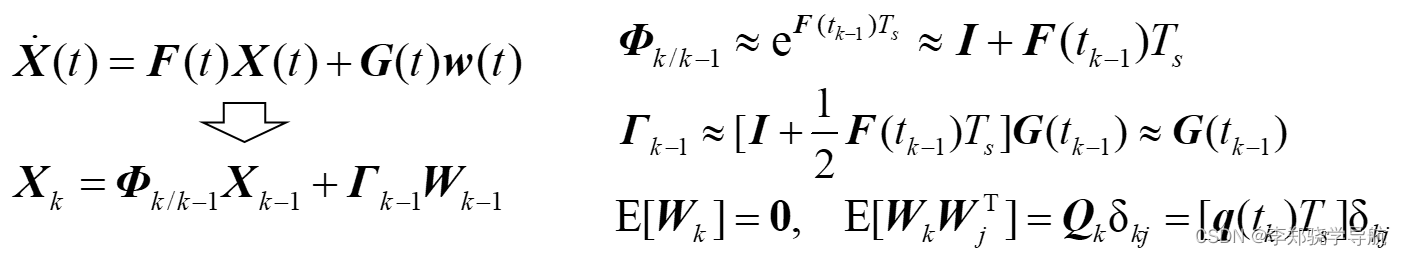
或等价表示为：

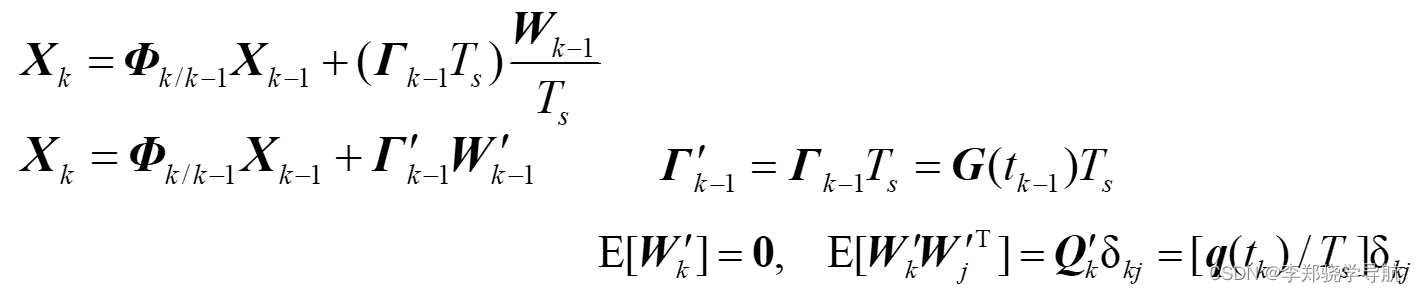
两者都满足：
$$\mathrm{E}\left[\left({\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\right){\left({\mathbf{\Gamma }}_{k-1}{\mathbf{W}}_{k-1}\right)}^{\mathrm{T}}\right]=\mathbf{G}\left(t_{k-1}\right)\cdot \left[\mathbf{q}\left(t_{k-1}\right)T_s\right]\cdot {\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)=\mathrm{E}\left[\left({\mathbf{\Gamma }}_{k-1}^{\prime }{\mathbf{W}}_{k-1}^{\prime }\right){\left({\mathbf{\Gamma }}_{k-1}^{\prime }{\mathbf{W}}_{k-1}^{\prime }\right)}^{\mathrm{T}}\right]$$

5、常见简单随机过程离散化

1.一阶马尔可夫：$\dot{X}(t)=-\beta X(t)+w(t)X_k=a_1{X}_{k-1}+W_{k-1}$

2.二阶马尔可夫：$\ddot{X}(t)=-2\beta \dot{X}(t)-{\beta }^{2}X(t)+w(t)X_k=a_1{X}_{k-1}+a_2{X}_{k-2}+W_{k-1}$

3.随机游走：$\dot{X}(t)=w(t)X_k=X_{k-1}+W_{k-1}$

4.随机常值：$\dot{X}(t)=0X_k=X_0$

6、实际物理信号的噪声单位

• $\tau$ 表示相关时间，很多时候等于 $1$，所以 $-1/\tau$ 可能被省略
• $\sqrt{q}-\mathrm{U}/\mathrm{s}/\sqrt{Hz}$ 为激励噪声密度，描述激励噪声本身。$\mathrm{U}/\sqrt{S}$ 随机游走噪声系数，是想描述 $X$ 的噪声。描述的主体不同。比如惯导中有：

二、连续时间量测方程离散化

连续量测方程的只是理论上的抽象，没有实际意义

连续量测模型：
$$\mathbf{Z}(t)=\mathbf{H}(t)\mathbf{X}(t)+\mathbf{v}(t)\mathrm{E}[\mathbf{v}(t)]=0,\mathrm{E}\left[\mathbf{v}(t){\mathbf{v}}^{\mathrm{T}}(\tau )\right]=\mathbf{r}(t)\delta (t-\tau )$$
在 $t_{k-1}$ 到 $t_k$ 时间段，两边积分平均：
$$\frac{1}{T_s}{\int }_{t_{k-1}}^{t_k}\mathbf{Z}(\tau )\mathrm{d}\tau =\frac{1}{T_v}{\int }_{t_{k-1}}^{t_k}\mathbf{H}(\tau )\mathbf{X}(\tau )+\mathbf{v}(\tau )\mathrm{d}\tau =\frac{1}{T_v}{\int }_{t_{k-1}}^{t_k}\mathbf{H}(\tau )\mathbf{X}(\tau )\mathrm{d}\tau +\frac{1}{T_s}{\int }_{t_{k-1}}^{t_k}\mathbf{v}(\tau )\mathrm{d}\tau$$
离散化记为：${\mathbf{Z}}_k\approx {\mathbf{H}}_k{\mathbf{X}}_k+{\mathbf{V}}_k$

观测噪声均值：
$$\mathrm{E}\left[{\mathbf{V}}_k\right]=\mathrm{E}\left[\frac{1}{T_s}{\int }_{t_{k-1}}^{t_k}\mathbf{v}(\tau )\mathrm{d}\tau \right]=\frac{1}{T_s}{\int }_{t_{k-1}}^{t_k}\mathrm{E}[\mathbf{v}(\tau )]\mathrm{d}\tau =0$$
观测噪声协方差：
$$\begin{array}{rl}\mathrm{E}\left[{\mathbf{V}}_k{\mathbf{V}}_j^{\mathrm{T}}\right]& =\mathrm{E}\left[\left(\frac{1}{T_s}{\int }_{t_{k-1}}^{t_k}\mathbf{v}(\tau )\mathrm{d}\tau \right){\left(\frac{1}{T_s}{\int }_{t_{j-1}}^{t_j}\mathbf{v}(s)\mathrm{d}s\right)}^{\mathrm{T}}\right]\\ & =\frac{1}{T_s^2}{\int }_{t_{k-1}}^{t_k}{\int }_{t_{j-1}}^{t_j}\mathrm{E}\left[\mathbf{v}(\tau ){\mathbf{v}}^{\mathrm{T}}(s)\right]\mathrm{d}s\mathrm{d}\tau =\frac{1}{T_s^2}{\int }_{t_{k-1}}^{t_k}{\int }_{t_{j-1}}^{t_j}\mathbf{r}(\tau )\delta (s-\tau )\mathrm{d}s\mathrm{d}\\ & =\frac{1}{T_s^2}{\int }_{t_{k-1}}^{t_k}\mathbf{r}(\tau ){\delta }_{kj}\mathrm{d}\tau \approx \frac{\mathbf{r}\left(t_k\right)}{T_s}{\delta }_{kj}\triangleq {\mathbf{R}}_k{\delta }_{kj}\end{array}$$
离散化量测间隔越小，等效出来的量测方差 ${\mathbf{R}}_k$ 越大

三、连续时间Kalman滤波

连续的函数可以认为是离散函数，但离散间隔 $t_{k-1}$ 到 $t_k$ 趋于 $0$ ；推导不是太严格，但比较直观。

1、连续状态空间模型

函数模型：
$$\{\begin{array}{l}\dot{\mathbf{X}}(t)=\mathbf{F}(t)\mathbf{X}(t)+\mathbf{G}(t)\mathbf{w}(t)\\ \mathbf{Z}(t)=\mathbf{H}(t)\mathbf{X}(t)+\mathbf{v}(t)\end{array}$$
随机模型：
$$\{\begin{array}{l}\mathrm{E}[\mathbf{w}(t)]=0,\mathrm{E}\left[\mathbf{w}(t){\mathbf{w}}^{\mathrm{T}}(\tau )\right]=\mathbf{q}(t)\delta (t-\tau )\\ \mathrm{E}[\mathbf{v}(t)]=0,\mathrm{E}\left[\mathbf{v}(t){\mathbf{v}}^{\mathrm{T}}(\tau )\right]=\mathbf{r}(t)\delta (t-\tau )\\ \mathrm{E}\left[\mathbf{w}(t){\mathbf{v}}^{\mathrm{T}}(\tau )\right]=0\end{array}$$

2、离散时间Kalman滤波

1. 状态一步预测：${\hat{\mathbf{X}}}_{k/k-1}={\mathbf{\Phi }}_{k/k-1}{\hat{\mathbf{X}}}_{k-1}$
2. 状态一步预测均方误差：${\mathbf{P}}_{k/k-1}={\mathbf{\Phi }}_{k/k-1}{\mathbf{P}}_{k-1}{\mathbf{\Phi }}_{k/k-1}^{\mathrm{T}}+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}$
3. 滤波增益：${\mathbf{K}}_k={\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}{\left({\mathbf{H}}_k{\mathbf{P}}_{k/k-1}{\mathbf{H}}_k^{\mathrm{T}}+{\mathbf{R}}_k\right)}^{-1}$
4. 状态估计：${\hat{\mathbf{X}}}_k={\hat{\mathbf{X}}}_{k/k-1}+{\mathbf{K}}_k\left({\mathbf{Z}}_k-{\mathbf{H}}_k{\hat{\mathbf{X}}}_{k/k-1}\right)$
5. 状态估计均方误差：${\mathbf{P}}_k=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right){\mathbf{P}}_{k/k-1}$

3、增益矩阵的连续化

将离散方程里的量测噪声 ${\mathbf{R}}_k$ 换成连续方程里的 $\frac{\mathbf{r}\left(t_k\right)}{T_s}$ 得：
$${\mathbf{K}}_k={\mathbf{P}}_k{\mathbf{H}}_k^{\mathrm{T}}{\mathbf{R}}_k^{-1}={\mathbf{P}}_k{\mathbf{H}}_k^{\mathrm{T}}{\left[\frac{\mathbf{r}\left(t_k\right)}{T_s}\right]}^{-1}=T_s{\mathbf{P}}_k{\mathbf{H}}_k^{\mathrm{T}}{\mathbf{r}}^{-1}\left(t_k\right)$$
将 $T_s$ 除到左边，求 $T_s$ 趋于 $0$ 的极限：
$$\mathbf{K}(t)=\underset{T_s\to 0}{\lim }\frac{{\mathbf{K}}_k}{T_s}=\underset{T_s\to 0}{\lim }{\mathbf{P}}_k{\mathbf{H}}_k^{\mathrm{T}}{\mathbf{r}}^{-1}\left(t_k\right)=\mathbf{P}(t){\mathbf{H}}^{\mathrm{T}}(t){\mathbf{r}}^{-1}(t)$$
即离散方程的增益 $K_k$ 除以时间间隔 $T_s$ 记成连续方程的增益；如果 $T_s$ 趋于 $0$ ,$K_k$ 也趋于 0，时间很短，预测很小，量测的修正自然也很小。

4、状态估计的连续化

将一阶的状态转移矩阵带入：
$$\begin{array}{rl}{\hat{\mathbf{X}}}_k& ={\mathbf{\Phi }}_{k/k-1}{\hat{\mathbf{X}}}_{k-1}+{\mathbf{K}}_k\left({\mathbf{Z}}_k-{\mathbf{H}}_k{\mathbf{\Phi }}_{k/k-1}{\hat{\mathbf{X}}}_{k-1}\right)\\ & =\left[\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)T_s\right]{\hat{\mathbf{X}}}_{k-1}+{\mathbf{K}}_k\left\{{\mathbf{Z}}_k-{\mathbf{H}}_k\left[\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)T_s\right]{\hat{\mathbf{X}}}_{k-1}\right\}\\ & ={\hat{\mathbf{X}}}_{k-1}+\mathbf{F}\left(t_{k-1}\right){\hat{\mathbf{X}}}_{k-1}{T}_s+{\mathbf{K}}_k\left[{\mathbf{Z}}_k-{\mathbf{H}}_k{\hat{\mathbf{X}}}_{k-1}-{\mathbf{H}}_k\mathbf{F}\left(t_{k-1}\right){\hat{\mathbf{X}}}_{k-1}{T}_s\right]\end{array}$$
将 ${\hat{\mathbf{X}}}_{k-1}$ 减到左边， $k$ 时刻的值，减去 $k-1$ 时刻的值，除以 $T_s$，求 $T_s$ 趋于 $0$ 的极限，就是连续的方程：
$$\begin{array}{rl}\dot{\hat{\mathbf{X}}}(t)& =\underset{T_s\to 0}{\lim }\frac{{\mathbf{X}}_k-{\mathbf{X}}_{k-1}}{T_s}=\underset{T_s\to 0}{\lim }\mathbf{F}\left(t_{k-1}\right){\hat{\mathbf{X}}}_{k-1}+\frac{{\mathbf{K}}_k}{T_s}\left[{\mathbf{Z}}_k-{\mathbf{H}}_k{\hat{\mathbf{X}}}_{k-1}-{\mathbf{H}}_k\mathbf{F}\left(t_{k-1}\right){\hat{\mathbf{X}}}_{k-1}{T}_s\right]\\ & =\mathbf{F}(t)\hat{\mathbf{X}}(t)+\mathbf{K}(t)[\mathbf{Z}(t)-\mathbf{H}(t)\hat{\mathbf{X}}(t)]\end{array}$$

5、均方差阵的连续化

将一阶的状态转移矩阵带入：
$$\begin{array}{rl}{\mathbf{P}}_k& =\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right)\left({\mathbf{\Phi }}_{k/k-1}{\mathbf{P}}_{k-1}{\mathbf{\Phi }}_{k/k-1}^{\mathrm{T}}+{\mathbf{\Gamma }}_{k-1}{\mathbf{Q}}_{k-1}{\mathbf{\Gamma }}_{k-1}^{\mathrm{T}}\right)\\ & =\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k\right)\left\{\left[\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)T_s\right]{\mathbf{P}}_{k-1}{\left[\mathbf{I}+\mathbf{F}\left(t_{k-1}\right)T_s\right]}^{\mathrm{T}}+\mathbf{G}\left(t_{k-1}\right)\cdot \mathbf{q}\left(t_{k-1}\right)T_s\cdot {\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)\right\}\\ & ={\mathbf{P}}_{k-1}+\mathbf{F}\left(t_{k-1}\right){\mathbf{P}}_{k-1}{T}_s+{\mathbf{P}}_{k-1}{\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right)T_s+\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)T_s+O\left(T_s^2\right)-{\mathbf{K}}_k{\mathbf{H}}_k\left[{\mathbf{P}}_{k-1}+O\left(T_s\right)\right]\end{array}$$
同理，将 $P_{k-1}$ 减到左边， $k$ 时刻的值，减去 $k-1$ 时刻的值，除以 $T_s$，求 $T_s$ 趋于 $0$ 的极限，就是连续的方程：
$$\begin{array}{rl}\dot{\mathbf{P}}(t)& =\underset{T_s\to 0}{\lim }\frac{{\mathbf{P}}_k-{\mathbf{P}}_{k-1}}{T_s}=\underset{T_s\to 0}{\lim }\mathbf{F}\left(t_{k-1}\right){\mathbf{P}}_{k-1}+{\mathbf{P}}_{k-1}{\mathbf{F}}^{\mathrm{T}}\left(t_{k-1}\right)+\mathbf{G}\left(t_{k-1}\right)\mathbf{q}\left(t_{k-1}\right){\mathbf{G}}^{\mathrm{T}}\left(t_{k-1}\right)-\frac{{\mathbf{K}}_k}{T_s}{\mathbf{H}}_k{\mathbf{P}}_{k-1}\\ & =\mathbf{F}(t)\mathbf{P}(t)+\mathbf{P}(t){\mathbf{F}}^{\mathrm{T}}(t)+\mathbf{G}(t)\mathbf{q}(t){\mathbf{G}}^{\mathrm{T}}(t)-\mathbf{K}(t)\mathbf{H}(t)\mathbf{P}(t)\\ & =\mathbf{F}(t)\mathbf{P}(t)+\mathbf{P}(t){\mathbf{F}}^{\mathrm{T}}(t)-\mathbf{K}(t)\mathbf{r}(t){\mathbf{K}}^{\mathrm{T}}(t)+\mathbf{G}(t)\mathbf{q}(t){\mathbf{G}}^{\mathrm{T}}(t)\end{array}$$

此方程也称：矩阵黎卡蒂（Riccati）方程，下面简单介绍一下Riccati方程：

标量Riccati方程：

矩阵Riccati方程：
$$\dot{\mathbf{P}}(t)=\mathbf{F}(t)\mathbf{P}(t)+\mathbf{P}(t){\mathbf{F}}^{\mathrm{T}}(t)-\mathbf{P}(t){\mathbf{H}}^{\mathrm{T}}(t){\mathbf{r}}^{-1}(t)\mathbf{H}(t)\mathbf{P}(t)+\mathbf{G}(t)\mathbf{q}(t){\mathbf{G}}^{\mathrm{T}}(t)$$
Kalman滤波里的 $P$ 一定是对称阵，转置还是本身，所以都没写

简记为：$\dot{\mathbf{P}}=\mathbf{FP}+\mathbf{PF}{\mathbf{F}}^{\mathrm{T}}-\mathbf{P}\mathbf{RP}+\mathbf{Q}$

它的解等价于 (化非线性问题为线性求解)：
$$\mathbf{P}=\mathbf{Y}{\mathbf{D}}^{-1}\text{ 其中 }\left[\begin{array}{c}\dot{\mathbf{Y}}\\ \dot{\mathbf{D}}\end{array}\right]=\left[\begin{array}{cc}\mathbf{F}& \mathbf{Q}\\ \mathbf{R}& -{\mathbf{F}}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{l}\mathbf{Y}\\ \mathbf{D}\end{array}\right]$$

验证如下：
$$\begin{array}{rl}\mathbf{Y}& =\mathbf{PD}\\ \dot{\mathbf{Y}}& =\dot{\mathbf{P}}\mathbf{D}+\mathbf{P}\dot{\mathbf{D}}\\ \dot{\mathbf{P}}& =\dot{\mathbf{Y}}{\mathbf{D}}^{-1}-\mathbf{P}\dot{\mathbf{D}}{\mathbf{D}}^{-1}=(\mathbf{F}\mathbf{Y}+\mathbf{QD}){\mathbf{D}}^{-1}-\mathbf{P}\left(\mathbf{R}\mathbf{Y}-{\mathbf{F}}^{\mathrm{T}}\mathbf{D}\right){\mathbf{D}}^{-1}\\ & =\mathbf{F}\mathbf{Y}{\mathbf{D}}^{-1}+\mathbf{Q}-\mathbf{P}\mathbf{R}\mathbf{Y}{\mathbf{D}}^{-1}+\mathbf{P}{\mathbf{F}}^{\mathrm{T}}=\mathbf{FP}+\mathbf{Q}-\mathbf{P}\mathbf{R}\mathbf{P}+\mathbf{P}{\mathbf{F}}^{\mathrm{T}}\end{array}$$

但线性化后此矩阵微分方程没有初等解，只有毕卡积分级数解：

时变状态/矩阵方程 $\dot{\mathbf{X}}(t)=\mathbf{F}(t)\mathbf{X}(t)$ 的毕卡积分级数解：

上面方程两边积分得：
$$\mathbf{X}(t)=\mathbf{X}(0)+{\int }_0^t\mathbf{F}(\tau )\mathbf{X}(\tau )\mathrm{d}\tau$$
但此方程右边还含有未知量，迭代一次，将 $\mathbf{X}(\tau )$ 替换成上式
$$\mathbf{X}(t)=\mathbf{X}(0)+{\int }_0^t\mathbf{F}(\tau )\left[\mathbf{X}(0)+{\int }_0^{\tau }\mathbf{F}\left({\tau }_1\right)\mathbf{X}\left({\tau }_1\right)\mathrm{d}{\tau }_1\right]\mathrm{d}\tau$$
里面又含未知变量 $\mathbf{X}\left({\tau }_1\right)$ ，再进行替换。反复迭代，一直存在未知变量，最后就变成无穷级数，而且还是无穷重积分
$$\begin{array}{rl}& =\mathbf{X}(0)+{\int }_0^t\mathbf{F}(\tau )\mathrm{d}\tau \mathbf{X}(0)+{\int }_0^t\mathbf{F}(\tau ){\int }_0^{\tau }\mathbf{F}\left({\tau }_1\right)\mathbf{X}\left({\tau }_1\right)\mathrm{d}{\tau }_1\mathrm{d}\tau =\cdots \\ & =\left[\mathbf{I}+{\int }_0^t\mathbf{F}(\tau )\mathrm{d}\tau +{\int }_0^t\mathbf{F}(\tau ){\int }_0^{\tau }\mathbf{F}\left({\tau }_1\right)\mathrm{d}{\tau }_1\mathrm{d}\tau +{\int }_0^t\mathbf{F}(\tau ){\int }_0^{\tau }\mathbf{F}\left({\tau }_1\right){\int }_0^{{\tau }_1}\mathbf{F}\left({\tau }_2\right)\mathrm{d}{\tau }_2\mathrm{d}{\tau }_1\mathrm{d}\tau +\cdots \right]\mathbf{X}(0)\end{array}$$
前面括号内的矩阵就是从 $0$ 时刻转移到 $t$ 时刻的状态转移矩阵：
$$\mathbf{\Phi }(t,0)=\mathbf{I}+{\int }_0^t\mathbf{F}(\tau )\mathrm{d}\tau +{\int }_0^t\mathbf{F}(\tau ){\int }_0^{\tau }\mathbf{F}\left({\tau }_1\right)\mathrm{d}{\tau }_1\mathrm{d}\tau +{\int }_0^t\mathbf{F}(\tau ){\int }_0^{\tau }\mathbf{F}\left({\tau }_1\right){\int }_0^{{\tau }_1}\mathbf{F}\left({\tau }_2\right)\mathrm{d}{\tau }_2\mathrm{d}{\tau }_1\mathrm{d}\tau +\cdots$$

可以省略高阶项进行近似，或者有时候高阶项就为 $0$

• 一般情况下不可交换 $\mathbf{F}(\tau )\mathbf{F}\left({\tau }_1\right)\ne \mathbf{F}\left({\tau }_1\right)\mathbf{F}(\tau )$, 上式即为最终毕卡级数解;

• 可交换时 $\mathbf{F}(\tau )\mathbf{F}\left({\tau }_1\right)=\mathbf{F}\left({\tau }_1\right)\mathbf{F}(\tau )$ (特殊如常值 $\mathbf{F}(\tau )=\mathbf{F})$, 才有闭合解:

  可交换时，多重积分等于单重积分的 $n$ 次方，除以 $n$ 的阶乘分之一

$$\begin{array}{l}{\int }_0^{{\tau }_1}\mathbf{F}\left({\tau }_1\right)\cdots {\int }_0^{{\tau }_n}\mathbf{F}\left({\tau }_n\right)\mathrm{d}{\tau }_n\cdots \mathrm{d}{\tau }_1=\frac{1}{n!}{\left[{\int }_0^{{\tau }_1}\mathbf{F}(\tau )\mathrm{d}{\tau }_1\right]}^n\\ \mathbf{\Phi }(t,0)=\mathbf{I}+\frac{1}{1!}{\int }_0^t\mathbf{F}(\tau )\mathrm{d}\tau +\frac{1}{2!}{\left[{\int }_0^t\mathbf{F}(\tau )\mathrm{d}\tau \right]}^2+\frac{1}{3!}{\left[{\int }_0^t\mathbf{F}(\tau )\mathrm{d}\tau \right]}^3+\cdots ={\mathrm{e}}^{{\int }_0^{t}F(\tau )\mathrm{d}\tau }40\end{array}$$

6、连续时间Kalman滤波方程汇总

$$\begin{array}{l}\mathbf{K}(t)=\mathbf{P}(t){\mathbf{H}}^{\mathrm{T}}(t){\mathbf{r}}^{-1}(t)\\ \dot{\hat{\mathbf{X}}}(t)=\mathbf{F}(t)\hat{\mathbf{X}}(t)+\mathbf{K}(t)[\mathbf{Z}(t)-\mathbf{H}(t)\hat{\mathbf{X}}(t)]\\ \dot{\mathbf{P}}(t)=\mathbf{F}(t)\mathbf{P}(t)+\mathbf{P}(t){\mathbf{F}}^{\mathrm{T}}(t)-\mathbf{K}(t)\mathbf{r}(t){\mathbf{K}}^{\mathrm{T}}(t)+\mathbf{G}(t)\mathbf{q}(t){\mathbf{G}}^{\mathrm{T}}(t)\end{array}$$

连续时间Kalman滤波方程中的状态估计和方差都是微分方程，相求结果得解微分方程。

离散时间Kalman滤波方程中的状态估计和方差可以认为是差分方程。

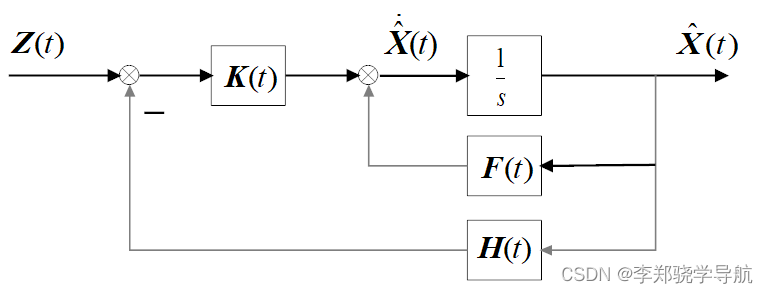
与确定性系统的状态观测器非常像