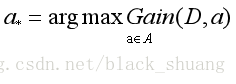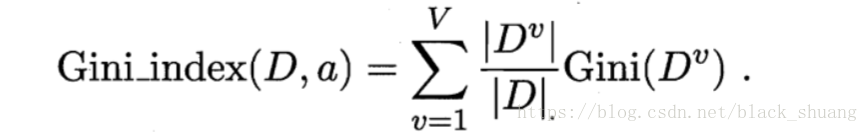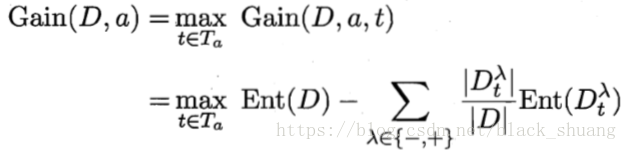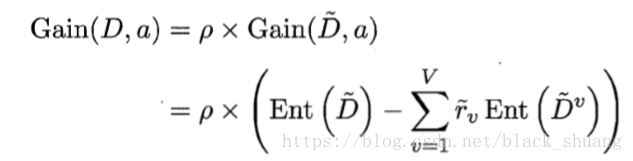前言
博主第一次接触机器学习,内容可能有许多原文复现,但是我尽量用自己的话来讲
读书笔记第一目的是为了总结,第二是顺便在博客上记录我的学习历程,同时也希望读者能有一点点收获吧~如果不对的地方,还请多多指教!
正文
周志华的机器学习第四章讲的是关于决策树。
1.决策树的基本流程
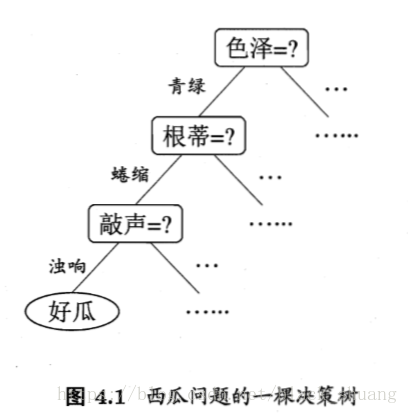
顾名思义,决策树就是基于树的结构来进行决策的。如图4.1所示,从树的根结点,到叶子结点(也就是判别结果),其中一般会经过若干个中间结点,每个中间结点对应一个属性测试,例如图中的色泽属性,根蒂属性,敲声属性。其中根结点是包含样本全集的,每经过一个中间结点,则会根据中间结点属性测试的结果划分到子结点中。
显然,对于每个样本,都有对应的属性集,例如图中的(色泽,根蒂,敲声),那么决策树的判别路径是如何规划的呢?是先判别色泽还是先判别根蒂?当前中间结点还有没有进一步生成子结点的必要?这就涉及到了路径的划分选择以及剪枝问题了。总的来说,一个决策树的基本流程是遵循简单且直观的“分而治之”策略,如图4.2所示。
从图4.2显然得出,决策树的生成是一个递归过程。什么叫递归过程呢?形象的来讲:决策树在生成过程中,从根结点开始,会一层一层往下延拓,生成更多的中间结点。易知由于样本的种类是有限的,样本的属性类别(色泽,纹理,敲声)等也是有限的,所以这颗决策树的层数(高度)以及每一层的中间结点数当然是有限的,而这个就依靠“递归条件”来限制这颗决策树的生成了。
例如在根节点的时候,经过递归条件判别“样本集是否全部都是一个种类的?” 如果是的话还有继续接下来按各种属性进行分类判别吗? 答案是“没有必要” 。 所以这个决策树的生成过程至此结束!因为我们就是要将样本分出类别来,而样本本来就是属于同一个类别的,所以没有继续分类的必要了。
在决策树的生成过程中,最重要的步骤之一就是步骤8,划分选择问题,这决定了这颗决策树的判别路径。

2.划分选择
首先明确决策树学习的目的是为了产生一颗泛化能力强的决策树。从根节点到每个叶子结点,我们都希望经过每个结点之后,分类结果会越来越清晰。例如在根节点时所有样本共有5类,经过第一个中间结点后,衍生了两个子结点,两个子结点的样本类别分别包含3类,换句话来说就是经过第一个中间结点,在一定程度上把部分不同类别的结点分开了,两个子结点中的样本类别纯度变高了。
让结点的“纯度”越来越高,就是划分选择问题的准则!
一般来讲,通过不同属性(色泽,纹理,敲声)的属性测试,在一定程度上都可以提升结点的纯度,狭路相逢勇者胜,我们必须从中挑出一个纯度提升效果最优的,那么该如何判别纯度提升效果最优呢?介绍三种判别准则:1.信息增益 2.增益率结合信息增益 3.基尼指数
而实际上,基于不同的准则,其实对泛化性能的影响是有限的,[Raileanu and Stoffel,2004]对信息增益以及基尼指数进行理论分是表明,在泛化性能方面两者仅有2%的不同。但是不同的准则对于决策树的尺寸会有较大影响,这就体现在了训练时间以及测试时间上。
2.1基于信息增益的划分选择
著名的ID3决策树学习算法就是以信息增益为准则来进行划分选择的。那么什么是“信息增益”?
我们先了解几个基础概念:
信息熵:一般来说,信息熵是用来量化信息的不确定性。什么叫不确定性能呢?
例如这样一则信息:”太阳从东边升起“ ,显然这则信息是所有人都知道的,是无可置疑的,所以我们认为该信息不确定性为0. 而“未来半个月内广州会下雨”,显然这个信息是未知的,不确定的,具有一定不确定性的。那么如何量化不确定性?
在数学上,一个离散随机变量X的熵H(x)定义为:
在决策树生成的应用中,假设当前样本集合D中第k类样本所占的比例为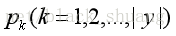
因此通过Ent(D)即可确定样本集合的纯度,纯度越高 ,集合的不确定性越小,信息熵越低。
前面已经陈述了,中间属性测试是根据样本的某一属性进行划分子结点的。不失一般性,设该属性为a,且a有V分可能取值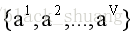
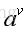
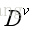
同样我们也可以对该子集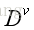
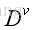

。换句话讲,这是在划分后的条件下的熵,我们可以称其为“条件熵”。
信息熵,条件熵的概念已经了解了,那么信息增益也就容易懂了:
信息增益就是指在某个条件下,该信息不确定性减小的多少。用公式来表达就是:信息增益=信息熵-条件熵。
信息增益越大,意味着在当前条件下,信息的不确定性减小的越多,不确定性越低,在本场景中就是样本的纯度越高。
因此我们就可以通过信息增益来进行决策树的划分属性选择,即在图4.2算法流程第8行选择属性
但是实际上,信息增益在一定程度上存在问题。例如集合D一共有100个样本,我们将样本从1-100进行编号。假如我们把编号也考虑进入属性划分选择,那么毫无疑问,编号带来的信息增益是特别高的。因为可想而知:一个样本一个编号,这个时候每个分支结点都只有一个样本,这已经是纯度最高的情况了。
换句话讲:信息增益倾向于可取数目较多的属性,这并不是我们期待的结果,所以引入了增益率。
2.2基于增益率与信息增益的划分选择
为了平衡信息增益倾向于可取数目较多的属性,增益率通过属性的“固有值“,属性a的可取数目越大,则IV(a)越大。定义增益率为:
属性固有值在分母,显然增益率倾向于可取数目较少的属性。
因此综合信息增益和增益率,得出了一种较均匀的划分原则:
先从候选划分属性中找出信息增益高于平均水平的属性,再从中找出增益率最高的。
2.3基于基尼系数的划分选择
同样是基于决策树的生成是希望分支结点的纯度越高越好这样一个原则,我们还可以通过基尼系数这一指标来衡量样本集合的纯度,基尼系数定义为:
从概率论来看,Gini(D)反应了从数据集中抽取两个样本,其类别不一致的概率。因此基尼系数越大,则表示样本集合的纯度越低。
因此经过划分后,产生v个分支结点的总基尼系数定义为:
于是,我们再候选属性集合中,选择那个使得基尼系数最小的作为最优划分属性。
3.剪枝问题
现在来考虑一个问题:决策树是不是形态越丰富,分支越多,越复杂,分类越准确呢?
显然是否定的。
学习算法中存在着一个需要特别注意的问题:“过拟合”。换句话说就是学习过程中过度的学习了训练集的特点,把训练集自身的一些特点当作所有样本数据都具有的一般性质,也就是学的太过了,有一些不应该继续分支的结点继续进行划分了,导致分支过多过冗余。这样子反而会降低学习算法的泛化能力。剪枝对于决策树的泛化性能的提升是显著的,有实验研究表明[Mingers,1989a],在数据带有噪声时,通过剪枝甚至可以将决策树的泛化性能提高25%
所以剪枝这一名词也因此得来,因为剪枝的目的就是剪去过多的分支!决策树剪枝的基本策略有“预剪枝”和“后剪枝”,两者的界定就是一个发生在决策树生成过程中,一个是发生在决策树生成后。
3.1预剪枝
预剪枝的定义就是在决策树生成的过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能的提升,则停止划分,并将当前结点标记为叶子结点。
我们可以通过留出法来对泛化性能进行评估。将样本集合分为训练集和验证集。在基于前面提到的几种属性划分选择的基础上,对比划分前后的验证集的准确率来进行泛化性能的评估。如果经过划分后,验证集的准确率提高了,则认为当前结点的划分对于泛化性能的提升是有意义的,否则不计划分。
通过预剪枝,不仅可以降低过拟合的风险,同时因为限制了无意义的结点划分,在训练和测试的计算成本上也有所优化。
由以上论述,我们可以认识到预剪枝是判断当前结点对于泛化性能的影响,并没有考虑当前结点的后续结点是否有机会能够提升泛化性能,这是一种“贪心”的本质。这个策略带来的问题就是有可能会丢失那些在后续确实能提高泛化性能的结点,因此预剪枝带来欠拟合的风险。
3.2后剪枝
后剪枝是发生于决策树生成完成以后,从由底至上考虑每个非叶节点,若将该结点替换为叶节点能够给决策树带来泛化性能的提升的话,则将该结点替换为叶节点。
因为后剪枝是在一棵完整的决策树的基础上从底至上考虑每个非叶节点,相对于预剪枝来说欠拟合风险很小,不过训练时间开销是比较大的。
4.连续与缺失值
至此,我们前面讨论的样本都是基于离散属性并且属性数据是完整的。然而实际上,现实世界中还是存在各种连续属性,而样本的属性有可能是会缺失的。所以这个部分主要就是讨论对于连续属性以及样本属性值缺失问题。
4.1连续值处理
前面讨论的划分选择问题,都是基于离散属性的。例如a有v个值,根据这v个值我们可以划分出v个分支结点。但是在连续属性的情况下呢? 显然不能这么执行,因为连续属性的可取数目是无限的,总不可能划分出无限个分支结点吧?
因此我们需要对连续属性进行处理,此时连续属性离散化技术可派上用场,其中最简单的策略就是采用二分法对连续属性进行处理。
给定样本集D和连续属性a,假定属性a在D上有n个取值,并且将取值从小到大排序,记为.二分法的思想就是设定一个划分点t,将D划分为子集
和
,
是包含那些在属性a上取值不大于t的样本,
是包含那些在属性a上取值大于t的样本。因为t取在
之间的任意一点所产生的划分效果都是一样的,我们不妨让t=
。基于这种划分方法,划分点t共有n-1个候选点,该候选划分点集合为:
。
我们假定通过信息增益进行划分选择,则对于连续属性来说,其信息增益计算易知如下:
即连续属性a的信息增益是基于通过二分法将连续属性离散化后选出最佳划分点的信息增益作为连续属性a的信息增益。
在这里有一点需要注意的是:
离散属性的划分中,作为当前结点划分依据的属性,再其分支结点将不再作为划分考虑。例如在判别西瓜的好坏分类中,我们第一个结点通过色泽分出了亮和暗,得出了亮和暗两个分支结点。那么接下来这两个分支结点将不再考虑西瓜的色泽属性了,因为在第一个结点已经明确划分出了哪些瓜是“亮”属性,哪些瓜是“暗“属性,离散属性的划分重点是判别”是什么“,所以不存在多次重复判别。
而连续属性不同,连续属性例如通过二分法来离散化,划分重点不是”是什么“,而是”区间内属性值的大小关系“,这是可以多次划分多次比较的。例如在区间0到1,第一个结点是以t=0.5进行划分,得出两个分支结点v1,v2。 在v1中0到0.5,我们可以再次选定一个划分点t=0.25,再次划分出分支结点。
这是连续属性与离散数学在划分时的一个区别。
4.2缺失值处理
在前面的讨论中,我们都是假定样本属性的值都不是缺失的,但现实情况下还是存在一些样本是缺失的。例如由于测试成本,隐私保护等等。
如果缺失属性样本较多的话,并且不做任何处理,简单的放弃不完整样本的话,显然对数据信息是极其浪费的。样本不能放弃,但是属性缺失我们不得不放弃,因为本身就缺失,我们不可能凭空随便插入一个值,所以我们只能在划分过程中进行处理,减小划分误差。总的来说需要我们考虑的问题有两个:
(1)如何在属性值缺失的情况下进行划分属性选择?
(2)给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
先讨论问题(1):
我们给定训练集D和属性a,令表示D中在属性a上没有缺失值的样本集合,显然我们只能通过
来判断属性a的优劣。假定属性a有V个可取值
,令
表示
在属性a上取值为
的样本子集,
表示
中属于第k类(k=1,2,...,|y|)的样本子集。假定我们为每个样本x赋予一个权重Wx,初值为1。同时定义:
①,表示对于属性a,无缺失的样本比例
②,表示无缺失样本中,第k类所占比例
③,表示无缺失样本在属性a上取值为
的样本的比例
一般来讲,样本具有多个属性。不同属性的缺失值情况不同。直观上来看:假如100个样本中,属性a的缺失值高达99份,属性b的缺失值只有1个,属性c的缺失值有50个。假定他们在没有缺失值的情况下对于样本集合的纯度提升效果一样,那在存在前面缺失的情况下,哪个属性最可靠?
可想而知最可靠的是属性b,其次是c,再其次是a。由此可以考虑给不同属性增加一个系数p=无缺失值总数/样本集合总数,例如此处举例Pa=1/100,Pb=99/100,Pc=50/100.
基于上述推论,我们可以将信息增益的计算时推广为:
其中系数也是与p出于相似的考虑。
对于问题(2):
出于缺失值的样本终归还是不是理想样本,估我们还是希望这样的非理想样本对于决策树的贡献减小,因此我们有如下策略:
若样本x在划分属性a上的取值已知,则将x划入与其对应的分支结点,并保持样本权重Wx不变。若样本x在划分属性a上的取值未知,则将样本x划入所有分支结点,且样本权重调整为*Wx。
5.多变量决策树
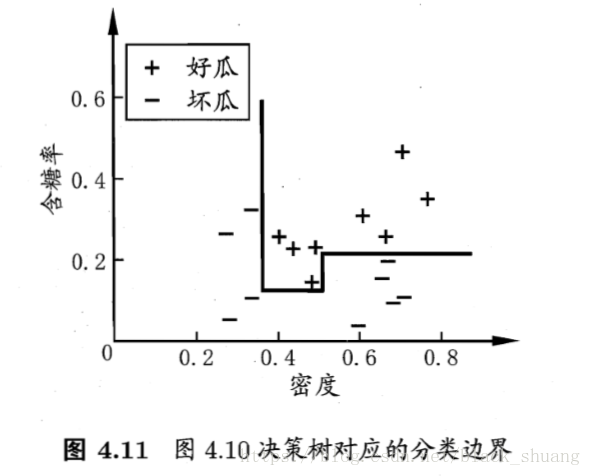
想象一下,若我们把样本的每个属性都视为坐标空间中的一个坐标轴,则由d个属性描述的样本就对应了d维空间中的一个数据点。对样本的分类就意味着在这个坐标空间中寻找不同类样本之间的分类边界。而我们前面提到的决策树在d维空间中形成的分类边界有一个特点:轴平行,如图4.11所示,这个样本集的属性只包括两个连续属性(密度,含糖率),它的分类边界由若干个与坐标轴平行的分段组成的。
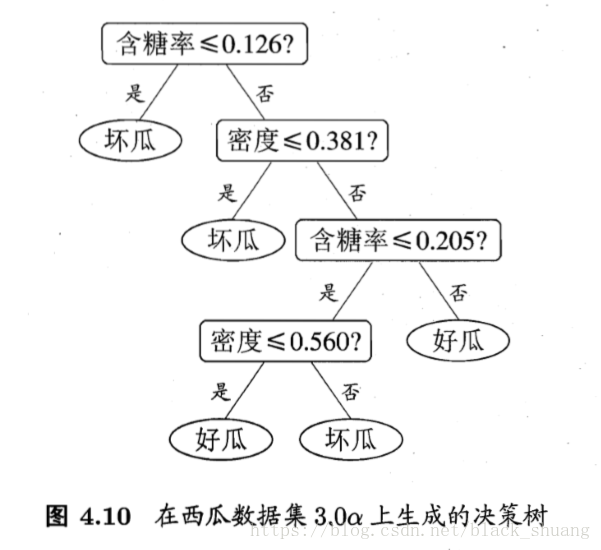
如图4.10以及4.11所示,在图4.10的决策树上有几个分支结点,对应图4.11则有几段关于轴平行的分类边界。这样的分类边界的确取得了很好的解释性,但是这仅仅是二维小样本容量上的应用。如果样本很复杂,是多维的大样本,那么必须通过很多很多段的划分才能取得较好的近似,例如图4.10中的决策树需要4段分类边界。通过多段的分类边界去划分,显然时间开销是很大的,因此假如我们不局限于平行与轴的分类边界,考虑使用斜的划分边界,如图4.12所示,此时就引入了“多变量决策树”。
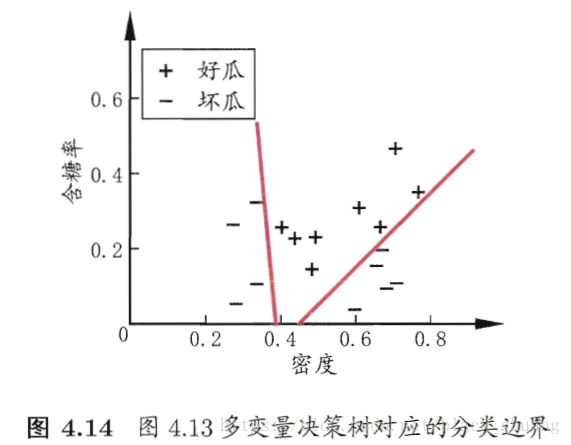
“多变量决策树”与“普通决策树”相比,关键在于分支结点的属性测试的区别。“多变量决策树”的属性测试不再是单一的属性测试,而是对多个属性的线性组合进行测试。换句话说,对于分支结点的属性测试,我们不再是为每个结点寻找一个最优划分属性了,而是对每个分支结点建立一个合适的线性分类器,例如图4.10中的数据集,我们通过多变量决策树生成如图4.13所示的决策树,并且其分类边界如图4.14所示。
显然与“普通的决策树分类边界”相比,采用“多变量决策树”能够通过斜的划分边界取得较好的效果。