数学的底层思维，到底是什么？

类比是我们最古老的思维方法之一，对于人类产生新发现起着重要的启发作用。我们常常认为自己熟悉类比推理，可有时却由于自身认知的限制拒绝接受显而易见的类比结论。

从远古时期开始，人类就开始了对月球的凝望。在很长一段时间里，人们认为月球是完美的，是神灵的领地，如果月亮的光晕平衡被打破，发生了月食，人类就需要用各种行动来纠正：中国人摔镜子，印加人大喊大叫，罗马人疯狂地挥舞火把。直到1609年伽利略将他的望远镜转向月球，才发现它并非平滑完美，而是布满混乱的峭壁和陨石坑。

与其他一些天文学家一样，伽利略在望远镜里看到了月球黑暗的部分里有一些光点，这些光点逐渐变大变亮，最后跟其他光亮的部分融为一体。伽利略觉得，这个现象很像早上的太阳照射在山上，太阳爬得越高，山谷的阴影缩得越小，最后整座山都沐浴在阳光之下。他认为，阴影和其它光学现象在地球和月球上应该是一样的。因此，伽利略下结论说月球表面一定不是光滑的，而是高高低低跟地球一样有山有谷。

这，就是类比的力量。

那什么是类比呢？

类比对两个事物进行比较，突出它们被认为相似的方面，其主要目的是为了用我们熟悉的事物去解释我们不熟悉的事物。类比推理是一种基于类比的思维方式，它根据两个（或两类）事物的某些属性相同或相似，推出它们另一属性也相同或相似，是一种由特殊到特殊的推理过程。

我国古代名著《战国策》中记载了一则邹忌的故事，算得是类比推理的绝佳案例。

邹忌修八尺有余，而形貌昳丽。朝服衣冠，窥镜，谓其妻曰：“我孰与城北徐公美？”其妻曰：“君美甚，徐公何能及君也？”城北徐公，齐国之美丽者也。忌不自信，而复问其妾曰：“吾孰与徐公美？”妾曰：“徐公何能及君也？”旦日，客从外来，与坐谈，问之客曰：“吾与徐公孰美？”客曰：“徐公不若君之美也。”明日徐公来，孰视之，自以为不如；窥镜而自视，又弗如远甚。暮寝而思之，曰：“吾妻之美我者，私我也；妾之美我者，畏我也；客之美我者，欲有求于我也。”

于是入朝见威王，曰：“臣诚知不如徐公美。臣之妻私臣，臣之妾畏臣，臣之客欲有求于臣，皆以美于徐公。今齐地方千里，百二十城，宫妇左右莫不私王，朝廷之臣莫不畏王，四境之内莫不有求于王：由此观之，王之蔽甚矣。”

在上面这则故事中，邹忌分析了自己的妻妾和客人对自己不说实话的原因，并把这一套推理用在了相似的场景（即齐威王与宫妇、朝臣、其他诸侯国的关系），得出“王之蔽甚矣”的结论，最终使得齐威王大力纳谏，成就伟业。

在前面伽利略的故事中，伽利略基于一个事实（阴影和光学现象不因地球和月球而变化）和相似的观测现象，推测出月球上也应和地球一样有山有谷的结论。

类比推理是人类思想的基础，可以说，也是一些非人类动物的基础。从人类发展历史来看，作为产生新发现的辅助手段，类比被广泛认为起着重要的启发式作用。化学先驱约瑟夫·普里斯特利（Joseph Priestley）认为，类比是所有探索研究的最佳指南，所有非偶然的发现都是在它的帮助下做出的。

在小学数学课本里，就有一个很好的类比的案例，即圆面积的推导方法和圆柱体的推导方法之间的类比。在推导圆的面积时，把圆切成了许多小扇形，最后拼成了一个近似的长方形。类似地，在推导圆柱体体积时，把圆柱切成了一个个小的柱体，最后拼成一个近似的长方体。

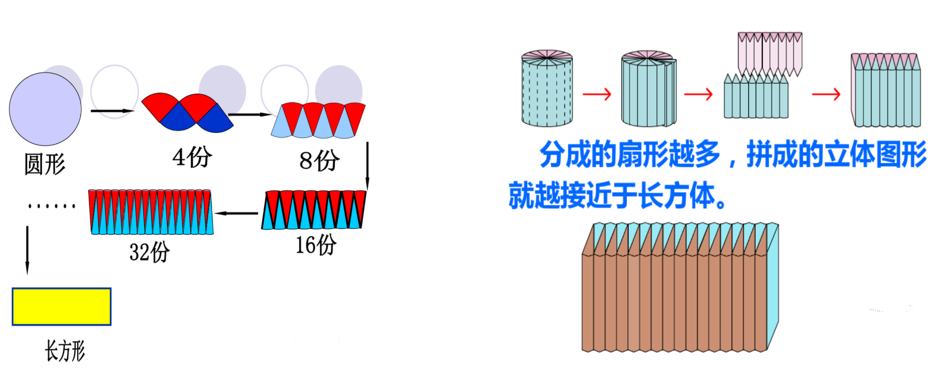
从类比的对象来看，类比可以分为：概念与操作的类比、结论的类比、方法的类比。

概念类比的一个典型例子是圆和球的定义。我们知道圆的定义是由所有到圆心的距离相等的点构成的集合（一条曲线），那么三维中球面的定义应该是由到球心的距离相等的点构成的集合（一个曲面）。

通过类比，我们往往可以发现一些新的结论。

比如，假设我们已知下面这个命题：在具有固定周长的所有长方形中，正方形的面积最大。

那能不能通过类比，将这个结论推广到三维空间呢？为此，我们首先得对涉及到这个命题的二维和三维的概念进行类比，如下表。

二维空间的概念	三维空间的概念
长方形	长方体
正方形	正方体
周长	表面积
面积	体积

由此，我们是不是可以推测出上面这个命题的三维类比结论：在具有固定表面积的所有长方体中，正方体的体积最大。

下面，我举几个类比推理的典型案例。

非十进制与十进制的类比

我们知道在十进制中，被9整除的数的特征是其各位数字之和能被9整除，其推理过程是基于数的位值表示，例如：

297=2×10²+9×10+7

=2×(99+1)+9×(9+1)+7

=2×99+9×9+2+9+7

因此，297能被9整除当且仅当其各位数字之和2+9+7能被9整除。

那么，我们是不是可以将这样的结论和推理过程推广到其它进制中呢？比如在7进制中，我们可以得到什么结论呢？

在这里，十进制的9应该对应于7进制的6，因此，我们可以大胆提出下面的类比结论：7进制中，被6整除的数的特征是各位数字之和能被6整除。

这个结论是否正确，我们也可以类比十进制的推理过程来进行验证。

435₍₇₎=4×100₍₇₎+3×10₍₇₎+5

=4×(66₍₇₎+1)+3×(6₍₇₎+1)+5

=4×66₍₇₎+3×6₍₇₎+4+3+5

因此，435₍₇₎能被6整除等价于4+3+5能被6整除。

我们也知道，十进制的循环小数化分数，有下面的结论：

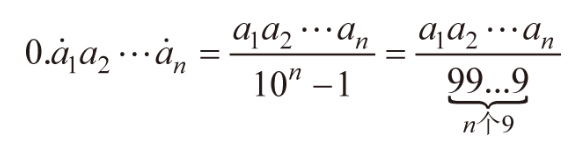
如果不采用无穷级数求和，推导过程如下：

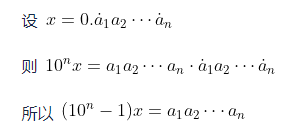
那对于其它进制，比如7进制的，也可以类比出类似的结论：

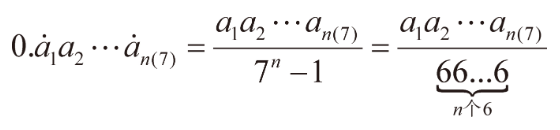
其推理方法，也完全可以类比十进制的推理：

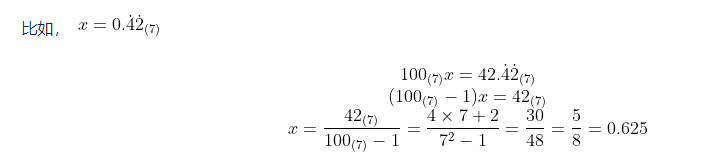
祖暅原理

祖暅原理是一则涉及几何求积的著名命题，它是这么说的：幂势既同，则积不容异”。“幂”是截面积，“势”是立体的高。意思是说界于两个平行平面之间的两个立体，被任一平行于这两个平面的平面所截，如果两个截面的面积相等，则这两个立体的体积相等。

那如果把这个原理应用到二维平面，能得出什么结论呢？

为此，首先我们得进行三维和二维概念上的类比:

三维中的概念	二维中的概念
立体	平面图形
体积	面积
截面	截线段
高	高
平行平面	平行线
平面	直线
面积	长度

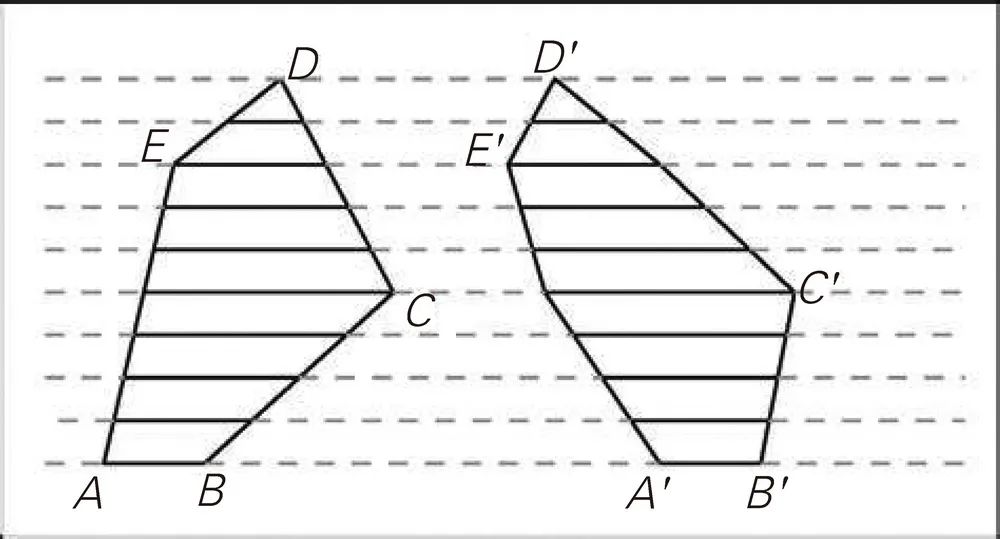
由此，我们可以得到祖暅原理的二维类比结论：界于两条平行线之间两个平面图形，被任一平行于这两条平行线的直线所截，如果两条截线段的长度相等，则这两个平面图形的面积相等。

三角形与四面体的重心

我们可以按下述方式找出三角形的重心：三角形的三条中线交于一点，这个点即为三角形的重心（如下图所示的G点）。

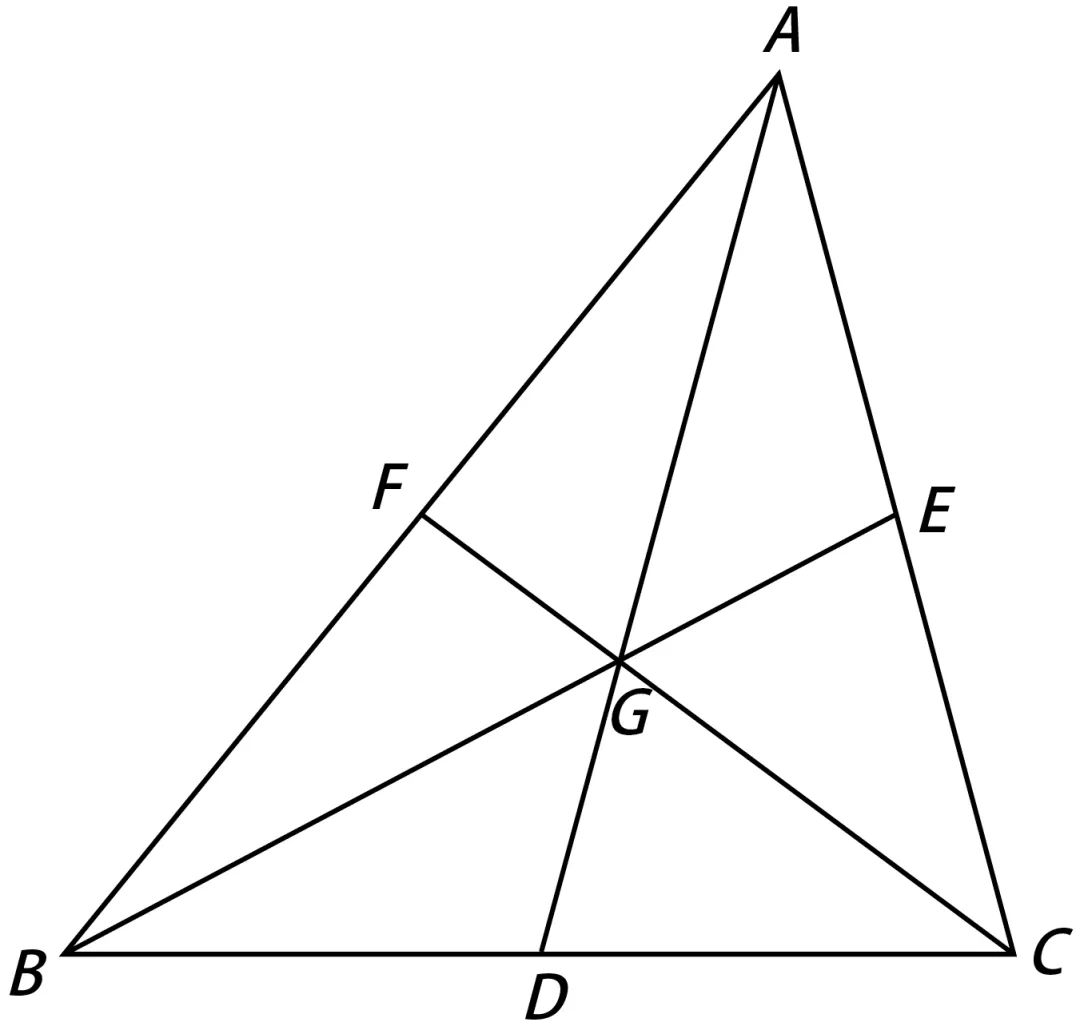
那对于四面体，是不是也可以类似地找到它的重心呢？

为此，我们也需要涉及概念上的类比。

二维中的概念	三维中的概念
三角形	四面体
中线	中面
直线与直线的交点	平面与平面的交线

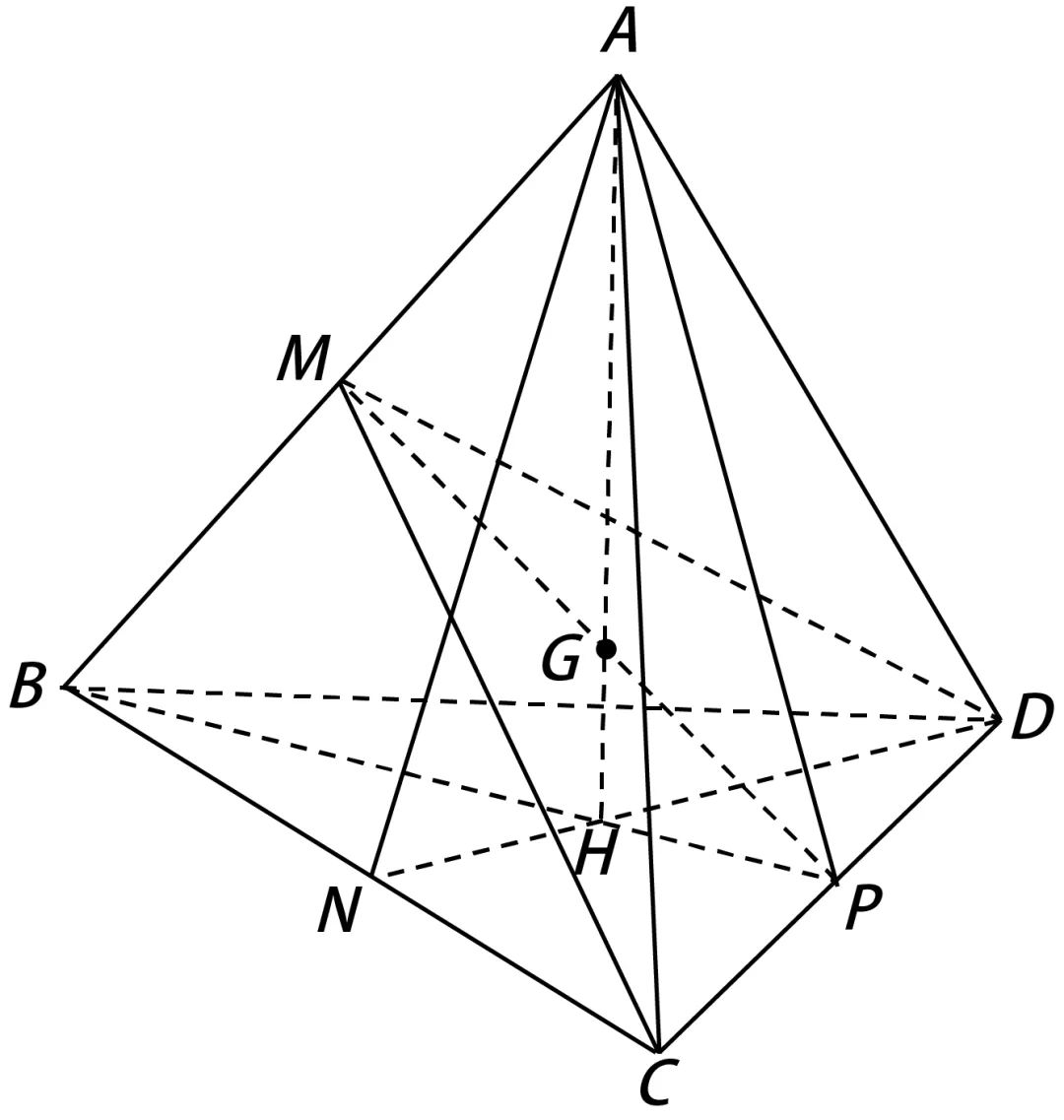
据此，我们可以进行这样的类比：将四面体一条棱和对棱的中点连接的三角形称为四面体的中面，那么一共有6个中面，这6个中面的交于一点，这个点就是四面体的重心。

虽然我们现在并不对6个中面是否交于一点这个结论进行证明，但至少我们预感这么类比出来的结论应该是对的。

微积分求面积与体积

在微积分求面积中，我们把平面图形看成是由无数个小的长方形组合而成的图形。（注：不要被微积分的名称所吓倒，其实微积分的原理小学生一般都能理解，圆的面积就是使用微积分思想来求的。）

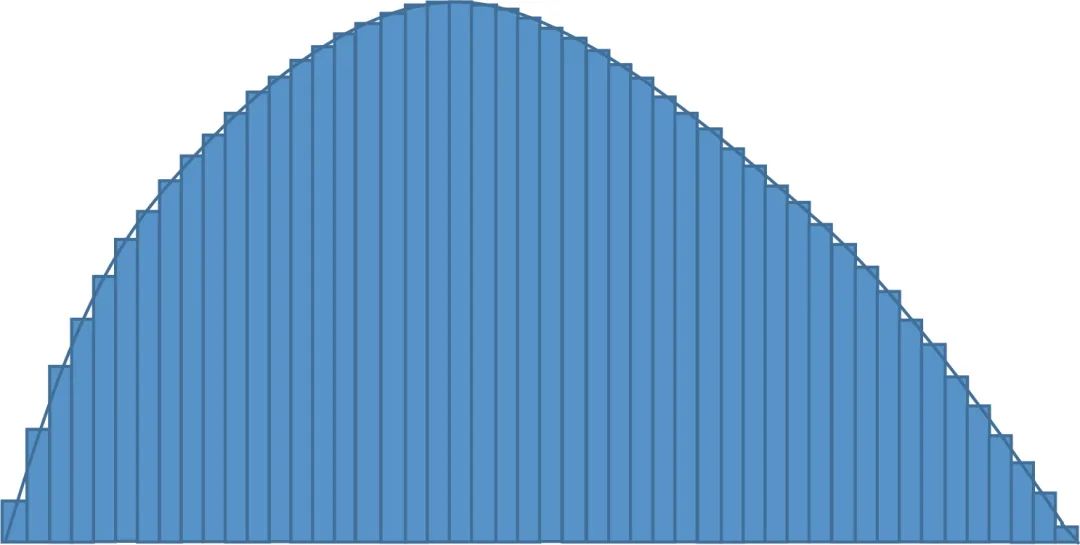
类比一下，我们可以把这种方法应用到三维空间中求物体的体积。这个时候，我们把立体图形看成是由无穷多个柱体组合而成的图形。这里，二维中的长方形就类比到了三维中的柱体。

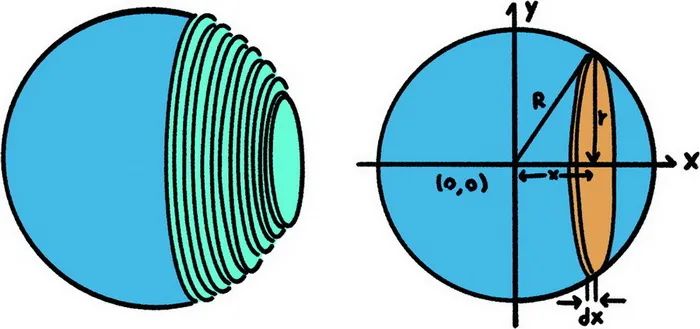
无限分割

下图的正方形边长为1，首先被分成四个相等的正方形，将左上角涂色，然后再将右下角的正方形一分为四，将左上角的涂色。如果我们一直持续这一过程，那么最后被涂色的部分占整个面积的多少？

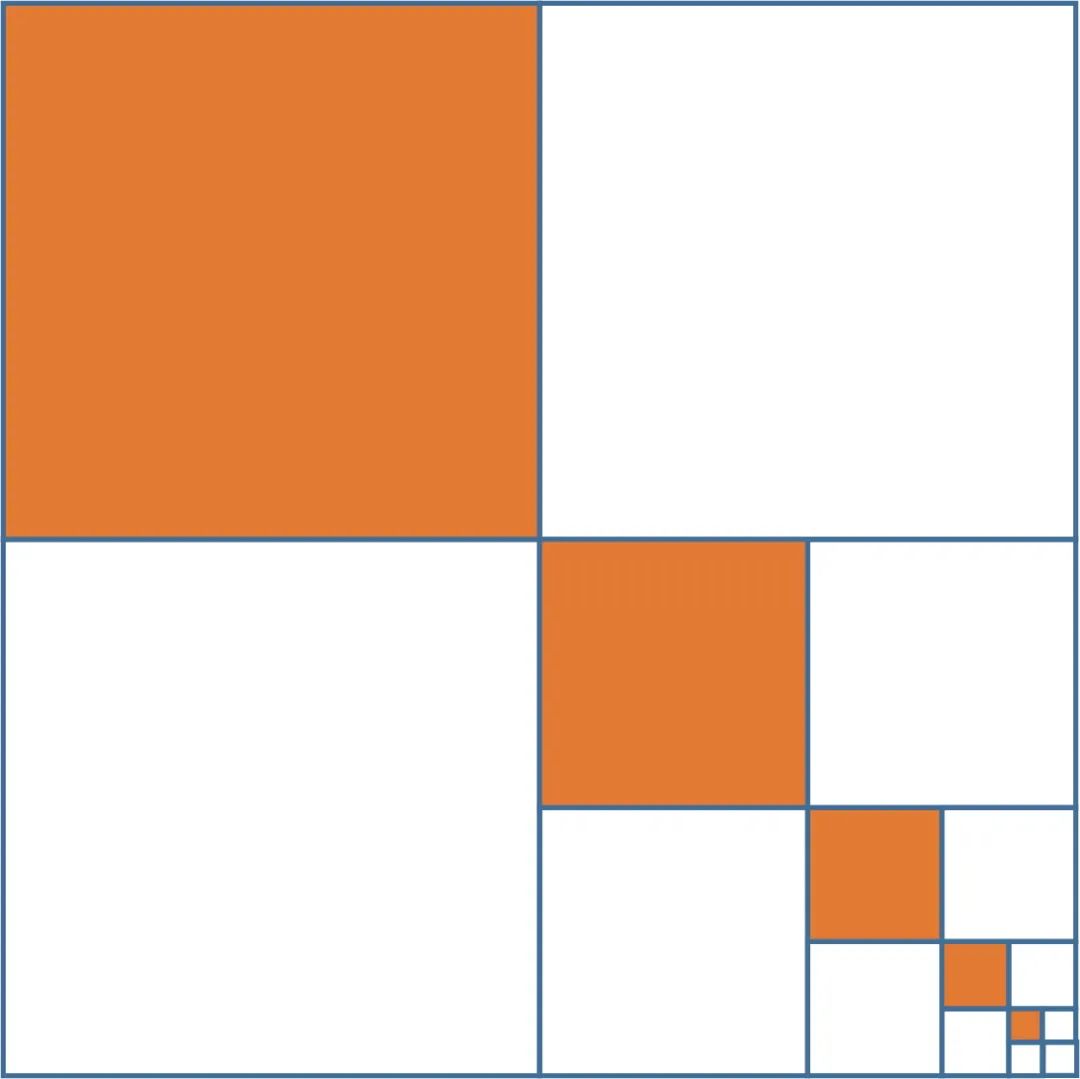
这个问题最直接的做法是用小学生不能理解的无穷级数求和。如果不用无穷级数求和，可以这么考虑：去掉右下角的1/4块后，剩下的这部分，涂色部分占1/3（如下图左）。

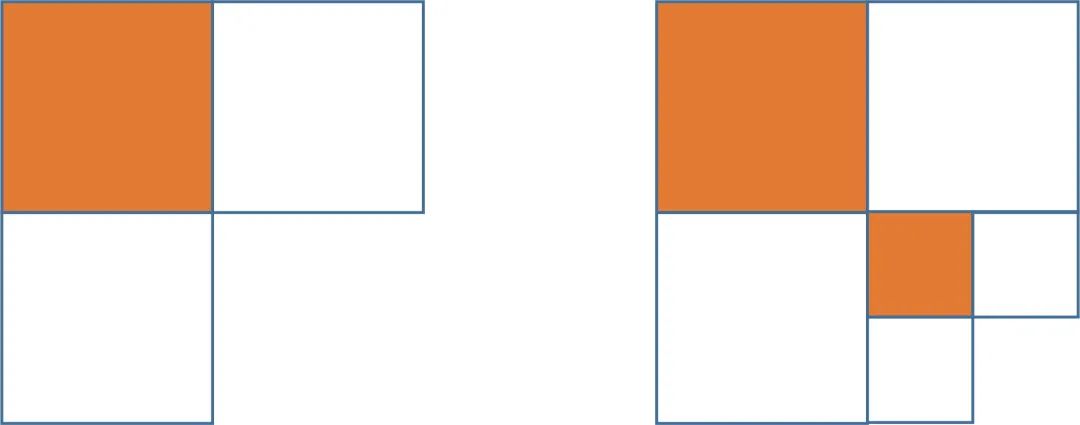
在剩下的1/4块里，我们再去掉这个1/4块的右下角，那么涂色部分依然占整个面积的1/3（如上图右）。依此类推，每次都抠掉右下角的一小块，涂色部分的面积在不同的尺度上都是整个面积的1/3，因此整体上涂色部分面积为整个正方形面积的1/3。

基于这个思路，我们是不是可以类比求解下面这个问题?

在下面的黄色正三角形ABC中，分别取三边的中点D,E,F并分别连接，然后分别取DE,EF,DF三边的中点H,I,G，并将ΔDGH,ΔEHI,ΔGIF涂成蓝色。接着，对中间的小三角形GHI重复上述同样的操作。如果这一操作一直持续下去到永远，请问，图中涂成黄色部分的面积占整个正三角形面积的几分之几？

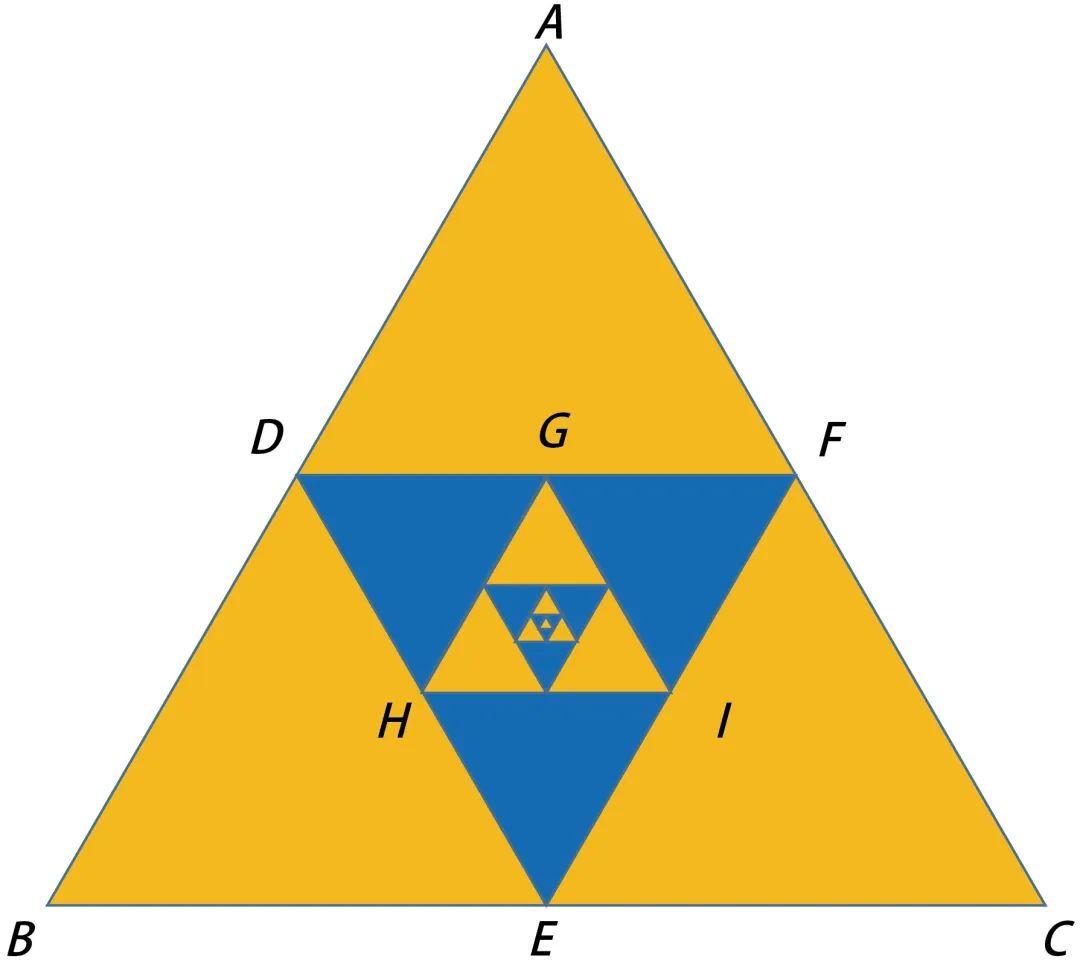
在这个问题中，三角形对应于前面问题中的正方形。在上面的问题解法中，我们在正方形中扣掉一块放大后与原来图形一样的部分（即右下角的1/4)，对应地，我们也找出这个图形中放大后与原图形一样的部分，显然是GHI对应的三角形。把它扣掉后，剩下的部分，黄色区域占比为12/15=4/5。因此，整个面积的占比也是4/5。

裂项

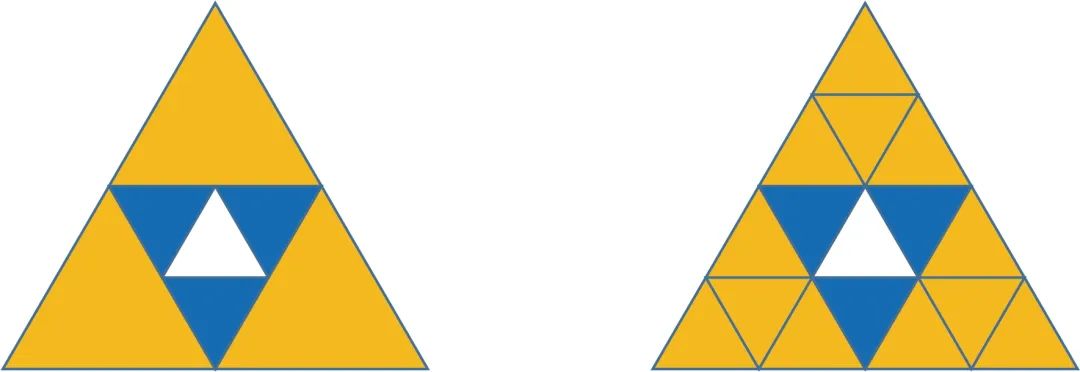
裂项是中小学数学中常见的技巧。一般课本上教的是最简单的分数裂项，分子只有两项相乘。但背后隐含了裂项的基本思想：把一项变成两项相减，以使得前后可以相消。

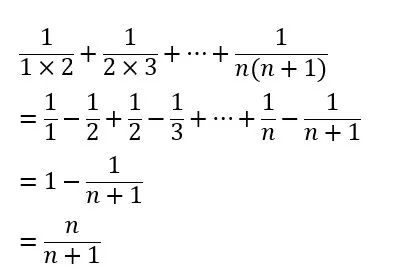
那么，类比一下，我们就也可以对分母是三个、四个或更多个等差的数相乘的分式进行裂项。

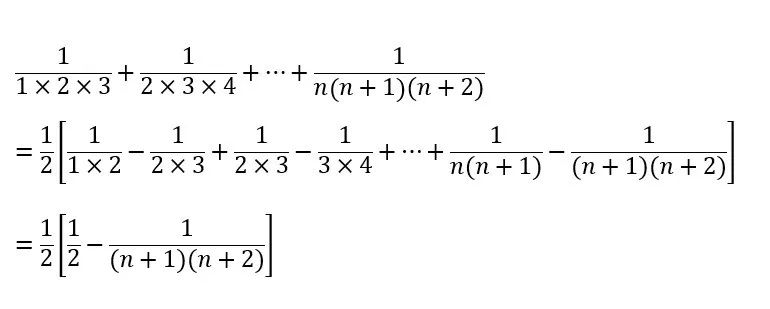
除了分数裂项，整数的乘积也可以裂项：

1×2+2×3+...+n(n+1)

我们可以把两个自然数相乘裂项成两个乘积之差，每个乘积都是3个自然数相乘，如下所示：

n(n+1)=[n(n+1)(n+2)-(n-1)n(n+1)]/3

那如果不是两个自然数相乘，而是三个或更多的自然数相乘呢？比如：

1×2×3+2×3×4+...+n(n+1)(n+2)

用分数裂项和上面的整数裂项类比一下，就不难得出下面的裂项：

n(n+1)(n+2)=[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]/4

直线分平面与平面分空间

我们再来看一个经典的问题：

n条直线最多把平面分成多少部分？

采用递归的思想，我们知道：n条直线最多把平面分成的块数为n-1条直线最多把平面分成的块数加n。从而，n条直线一共把平面分为1+1+2+3+⋯+n=n(n+1)/2+1块。验算一下：当n=1,2,3时，分别为2，4，7，满足。

解题到这儿当然不算结束，核心问题还没有解决。

我们刚才的归纳只是一种猜测，还需要证明其正确性。为什么n条直线最多分的块数是在n-1条直线最多分的块数基础上加n呢？这就涉及到“直线-交点-线段-平面”之间的关系。

我们知道，如果一条直线上有n个点，那么这些点将把这条直线分成n+1段。

原来有n-1条直线，加上第n条直线后，这第n条直线最多与之前的n-1条直线有n-1个交点，这些交点将把第n条直线分成n段。而每一段都将把原来的一个区域一分为二，因此多出了n块。下图给出了n=3的示意图。

我们完全可以把这个推理方法应用到非直线的平面图形划分平面的问题中，比如下面这个问题：

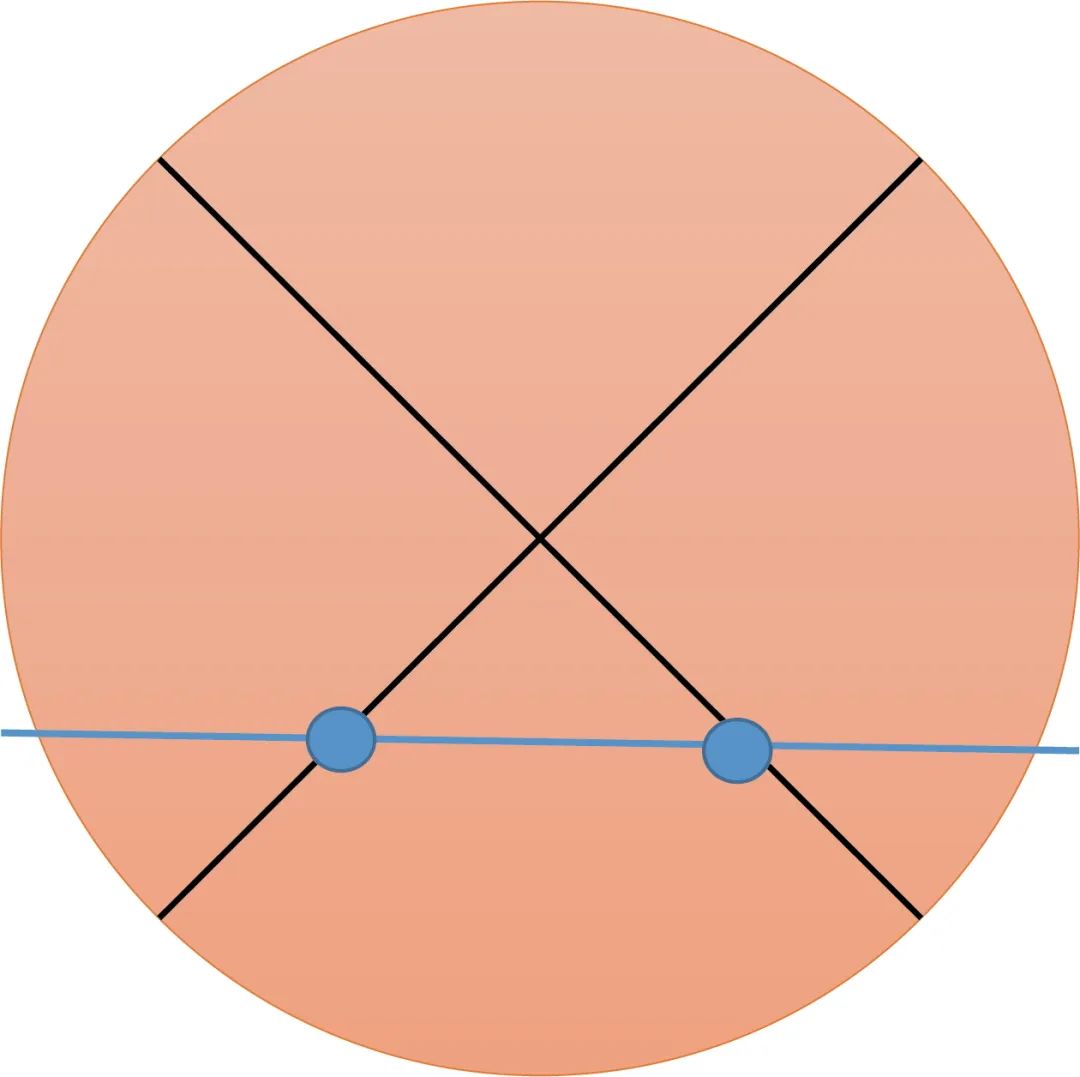
n个圆，最多把平面分成多少部分？

我们可以沿用之前的递归思想和“交点—线段—平面”的分析方法。如果在n-1个圆的基础上增加一个圆，那这个圆最多与前面的n-1个圆有2(n-1)个交点（如下图所示，第4个红色圆加上去后，最多与前面的3个圆都相交，一共有6个红色的交点），这2(n-1)个交点把第n个圆分成2(n-1)段（注：封闭图形），每一段都把原来的一块一分为二，因此最多多分出2(n-1)块。

据此，n个圆最多将平面分成:

1+1+2+4+…+2(n-1)=2+n(n-1) (n≥1)

如果增加一个维度，这个问题就变成了：

n个平面最多把空间分成多少部分？

如果我们从点分直线成线段、线段分平面成区域这一思想衍生过来，那我们就会发现这个平面分空间问题的求解思路也可以类比直线分平面的做法。首先，我们得做一些概念和操作上的类比。

二维中的概念和操作	三维中的概念和操作
直线	平面
交点	交线
点分直线成线段	线段分平面成区域
线段分平面为平面区域	平面分空间为空间区域

在直线分平面的问题中，我们通过多出的线段来分析增加一条直线后多分出的平面数；那么在平面分空间的问题中，我们是不是也可以通过多出的平面来分析增加一个平面后多分出的空间数呢？

我们还是采用递归的思想。我们知道3个平面最多将平面分成8块。在3个平面的基础上增加1个平面，前面3个平面最多和这个平面有3条交线，这三条交线将把这第4个平面最多分成7部分（由直线分平面的结论得到），每一个部分将把原来所在的空间一分为二，因此在8块的基础上多分出了7块，也就是说4个平面最多把空间分为8+7=15部分。

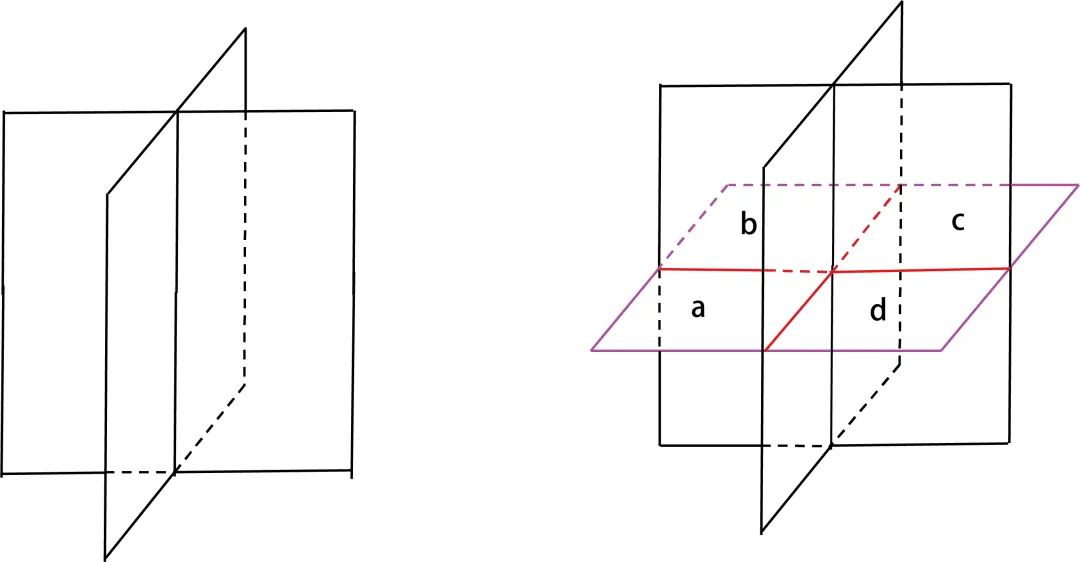
一般化地，第n个平面将和前面n-1个平面有n-1条交线，根据直线分平面，这n-1条交线最多把第n个平面分为n(n-1)/2+1个区域，从而能比n-1个平面多分出n(n-1)/2+1块空间。

因此，平面分空间满足下面的递推关系：

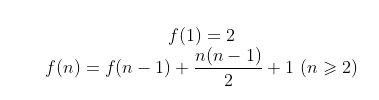
类比的不足

但是，由于类比推理的逻辑根据是不充分的，带有或然性，具有猜测性，它们的结论只是得到不同程度的支持，并不一定完全可靠。因此，类比只能作为一种发现的辅助手段，不能作为一种严格的数学方法。对于经过类比推理得出的结论，还需要经过严格的论证，才能确认猜测结论的正确性。

比如：“这篇小说只有1000字,文字很流畅，这篇小说得奖了。你写的这篇小说也是1000字，文字也很流畅，因此也一定能得奖。”这样的类比无疑会得出错误的结论。

历史上，18世纪的托马斯·里德关于其他行星上存在生命的论点也是基于类比推理。里德指出了地球和太阳系中其他行星之间的许多相似之处：所有行星都围绕轨道运行并被太阳照亮；有几个行星有卫星；全部都绕着轴旋转。因此，他总结说，"认为这些行星可能像我们的地球一样，是各种生物的栖息地，这并非没有道理"。最终，现代科学证明了这一类比结论是错误的。不过，即便如此，人类依然希望借助类比寻找适合生命存在的外星系类地行星。

并非每个人都真正懂得类比

到这里，或许很多人都会觉得类比已经是我们日常所掌握的思维方法了。但事实真的是这样吗？

小说《平面国》是19世纪一部畅想四维空间的先驱性作品，在小说的后半部分，作者大量使用了类比推理。

一直生活在平面国的主人公有一次梦见了直线国，试图向直线国的国王解释什么是二维平面，可再怎么解释都没能成功，只能作罢。

有一次，主人公在给自己的六边形孙子讲解几何学算术知识时，他那智慧的孙子提了个问题：如果把一个点移动3英寸，就能得到一条3英寸长的线段，可以把这条线段记作3；如果把一条3英寸长的线段平行移动3英寸，就能得到一个边长为3英寸的正方形，可以把这个正方形记作3的平方；既然如此，如果把一个边长为3英寸的正方形平行移动（也不知道怎么个平行移动法），就一定可以得到另外一个图形（不知道是什么图形）——这个图形每边的长度也是3英寸，而且这个图形一定可以被记作3的立方。

虽然主人公的孙子一直生活在平面国，没有见过立方体，但他却通过某种纯粹的思维推理预见了立方体的存在，这种推理方法，就是类比推理。

遗憾的是，主人公无法突破二维世界的禁锢。在他眼里，3的立方只有数字意义，没有几何学上的意义。他认为，那孩子可真是个傻瓜。

可正在这时，一个空间国的访客来到了。这个访客是这么描述自己的：从某个角度来看，我确实是一个圆形。我是比平面国中的任何一个圆都更加完美的圆。更准确地说，我是许多个圆合成的一个圆。

没错，这个访客就是球。

为了让书中这个固执的主人公理解什么是第三个维度，球也拿起了类比这一强大的武器。

球的类比推理在我们看来实在是太自然不过了，他是这么循循善诱的：

1. 一个点向北移动，并留下一条发光的轨迹，这条轨迹叫线段，一条线段有两个端点。

2. 这条南北向的线段沿东西方向平行移动，于是线段上的每个点都会在东西方向上留下一条直线形的轨迹。假设线段移动的距离与线段的原始长度相等，那么就得到了一个正方形。一个正方形有四条边和四个角。

到这个地方，平面国的主人公都能完全理解。

可接下来，球希望主人公发挥一下想象力，想象一下平面国中的一个正方形平行向上移动，也就是移到平面国以外去，这样，正方形中的每个点都不会经过其它点曾经占据过的地方。每个点留下的轨迹都是一条仅属于它自己的线段。

老实说，这是非常好的类比方式。但无奈的是，生活在平面国中的主人公无法想象移动到平面国以外是什么，他已经到了快被逼疯的边缘。但他还是强忍住不耐烦的心情，从而有了下面的对话。

主人公：既然您说向“上“移动正方形能产生一个新的图形，那么请问，这个图形究竟是什么性质的图形呢？我假定您总可以用平面国的语言来描述这个图形吧。

球：这个形状非常简单，只需要通过严格的类比就能推出——只是，顺便说一声，你不能把这个新的形状叫做“图形“，因为他是一个立体形。但是我可以向你描述这个新的形状。准确地说，我描述不了，但类比的方法可以让你明白这个新的形状是什么样的。

首先，假设我们有一个点。既然是一个点，那么他当然只有1个顶点。

通过移动一个点，可以得到一条线段。一条线段有2个顶点。

通过移动一条线段，可以得到一个正方形，一个正方形有4个顶点。

下面的问题，你自己可以回答了：1，2，4，这显然是一个几何级数。那么这个级数中的下一个数字是什么呢？

主人公：8。

球：完全正确。所以说，通过移动一个正方形，能够产生一个新的形状。现在你还不知道这个形状的名字，但我们空间国的人把他叫作“立方体“。一个立方体有8个顶点。现在你相信我所说的了吗？

主人公：既然您说这个新的形状有“顶点“，那想必就是我们说的”角“了。那么这个新玩意儿也有侧边吗？

球：当然有侧边。这一点通过类比就可以推演出来啊。但是，这个新形状的侧边其实不是你们所说的“侧边”，而是我们所说的“侧面”。一个侧面就相当于平面国中的一个实心图形。

主人公：那么，这个新的形状究竟有多少个实心图形，或者说有多少个侧面呢？

球：你怎么还问我？你不是数学家吗？恕我冒犯，我这么说吧：任何一个形状都可以看作是由一些‘侧元素’围成的，每个‘侧元素’的维度总是比这个形状的维度小1。因为1个点是零维的，所以点没有‘侧元素’；依此类推，线段有2个侧点，正方形有4条侧边；0，2，4，你把这个级数叫做什么？

主人公：算术级数。

球：那么这个级数里的下一个数字是多少？

主人公：6.

球：完全正确。你瞧，你自己就能回答这个问题吧。通过移动正方形产生的这个立方体是由6个侧面围成的，也就是说由6个你的内部围成的。现在你都明白了，对不对？

可是，主人公并没有明白。他已经快疯了，一边叫着“怪物”，一边说，“不管你是骗子、巫师、噩梦，还是魔鬼，我都不能再忍受你的恶作剧了。”

最后，球实在没有办法，只能付诸行动，把正方形主人公拉出了平面国，来到了空间国。眼见为实，在经历了巨大的震撼之后，主人公终于明白了空间国确实是存在的。此时，获得新知的主人公仿佛置身于天堂。他的心智被彻底点燃，他已经无法容忍某些专断独裁之人把维度限制在二维、三维，或者任何小于无限的维数。

于是，正当球还想继续向主人公传授规则立体形知识的时候，主人公鼓足勇气打断了球，并开启了下面的对话。

主人公：阁下，是您的智慧打开了我的心智，点燃了我的渴望。您让我想到，在您之上，还会有更伟大、更美丽、更接近完美的存在。您是由许多个圆合成的形状，您比我们平面国的所有居民都更高级；那么毫无疑问，在您之上，还有由许多个球体组成的至高存在，他会比空间国的任何一个立体形更加高级。我们现在正在空间国俯瞰平面国的一切，把所有平面图形的内部尽收眼底；既然如此，在我们之上，一定还有更高、更纯粹的空间——您一定也打算带我去那里看看吧。啊，不管是在怎样的维度中，您永远都是我的哲学导师和我的朋友。让我们一起去更高的地方，从更广阔的空间里，从更深邃的维度中俯瞰这一切吧。在那里，我们能看到立体形的内部，就连您的肠道，以及与您相似的其他球体的肠道也会变得一览无余。

可没想到，这次轮到球傻眼了。

球：可是你说的四维空间究竟在哪儿？

主人公：我不知道。但导师您一定知道吧。

球：我不知道。根本没有那么个地方。你的这个念头是完全不可想象的。

主人公：我们可以用类比的方法来论证四维形状的存在。

球：类比！胡说八道！什么类比！

主人公：阁下一定是在试探在下，看在下还记不记得您曾传给我的天启。

在一维空间中，移动一个点，不就能产生一条有2个端点的线段吗？

在二维空间中，移动一条线段，不是就能产生一个有4个顶点的正方形吗？

在三维空间中，移动一个正方形，不是就能产生一个有8个顶点的神圣生物——立方体吗？

那么在四维空间中，如果移动一个立方体，难道不会产生一个更加神圣的，有16个顶点的生物吗？

您瞧，数列的规律总归不会出错吧：2，4，8，16，这难道不是一个几何级数？这难道不是‘只需通过严格的类比就能推出’的结论吗?

一条线段有2个端点，一个正方形有4条侧边，因此一个立方体必然有6个侧面，这难道不是阁下教给我的知识吗？再瞧瞧这个数列的规律：2，4，6，难道不是一个算术级数吗？那么下一步我们必然能推出这样的结论：在四维空间中，神圣的立方体生出的更神圣的后代一定有8个侧体，难道不是这样吗？这可不就是阁下教导我的，‘只需通过严格的类比就能推出’的结论吗？

在四维空间，一个立方体在朝某种全新的方向移动，根据严格类比可知，立方体内的每一点都会穿过一种全新的空间，留下互不重叠的轨迹——这样就能创造出一个比立方体更加完美的形状，这个形状有16个顶点、16个立体角，而且有8个侧立方体围成。

下表总结了主人公的类比结论。

维度	名称	顶点	侧元素形状	侧元素个数
1	线段	2	点	2
2	正方形	4	线段	4
3	立方体	8	正方形	6
4	超立方体	16	正方体	8

主人公没想到，这次球却完全不能接受，一次又一次咆哮着叫主人公闭嘴。最后，一脚把主人公踹回了平面国。

读到这，我想起了一句话：夏虫不可语冰，井蛙不可语海。

我们嘲笑井蛙，可事实上我们每个人却又都是井蛙。虽然我们都知道类比，但并非每个人都真正懂得并能运用类比。我们可以在自己的认知范围内用类比向一个新人滔滔不绝地讲解我们所理解的事物，但却很难接受超越自身认知范围或环境限制的类比结论。

  推荐阅读

作者：昍爸、昍妈

数学之美是什么？数学之美在哪里？学会欣赏数学的美，才能真正理解数学

展现数学均衡有序的思维之美、简洁精确的逻辑之美、度量万物的直观之美、探索奥秘的创造之美