文章目录


- 要证明这个程序需要从上往下进行,先单独证明
f:=1, i:=1再单独证明while中的内容,while
中的内容需要一条条单独证明
霍尔三元组
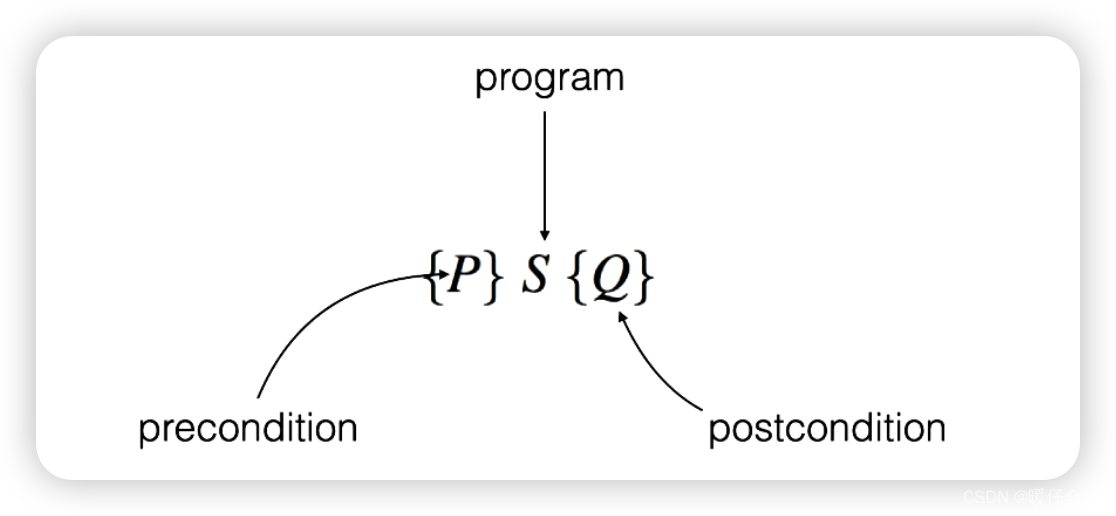
- 代表:当 P 满足,执行 S 后,Q 就会被满足(holds)
案例1
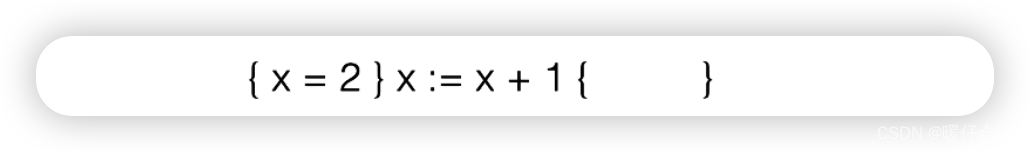
- 如果
x=2是满足的 - 那么经过表达式
x:=x+1之后,什么式子会hold?
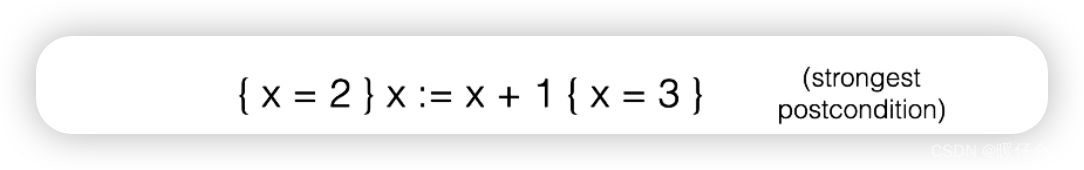
- 这里
x=3被称为是 ”给定x=2作为precondition条件下的strongest postcondition“
案例2
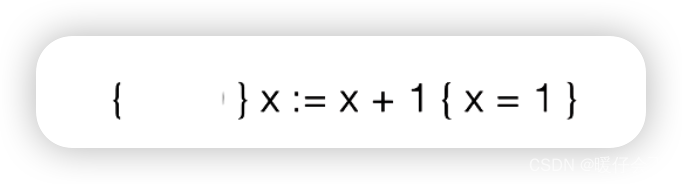
-
同样的方式:当
x=1作为postconditionholds的时候,precondition我们也很容易推出就是x=0

-
但是这里的
precondition被是weakestprecondition -
这是因为,我们反向推理(backwards) 的难度低于正向推理 (forward)
-
还有一种理解方法就是:
x > 5 = > x > 3 x>5 => x>3 x>5=>x>3 因此我们说 x > 5 x>5 x>5 是更加严格的条件;也就是更加strong的条件。同样的我们来看这个post condition -
如果我们能够通过
precondition得到x=3我们可以根据x=3这个条件推导出其他更加宽松的postcondition,比如 x > 2 x>2 x>2,此时我们的式子可以写成这样:
{ x = 2 } x : = x + 1 { x > 2 } \{x=2\} x:=x+1 \{x>2\} { x=2}x:=x+1{ x>2} -
这是完全没有问题的,而 x > 2 x>2 x>2 的条件是不如 x = 3 x=3 x=3
strong的 -
同样的道理我们看为什么是
weakest precondition:因为当我们用一个比现在precondition更严格一点的条件,这个推导式子也同样成立:
x + 1 = 3 = > x = 2 x+1=3 => x=2 x+1=3=>x=2 -
所以我们认为 x + 1 = 3 x+1=3 x+1=3 这个条件比 x = 2 x=2 x=2 严格,于是我们带到原式子中:
{ x + 1 = 3 } x : = x + 1 { x = 3 } \{x+1=3\} x:=x+1 \{x=3\} { x+1=3}x:=x+1{ x=3} -
这个式子当然也是成立的
逻辑

推导规则
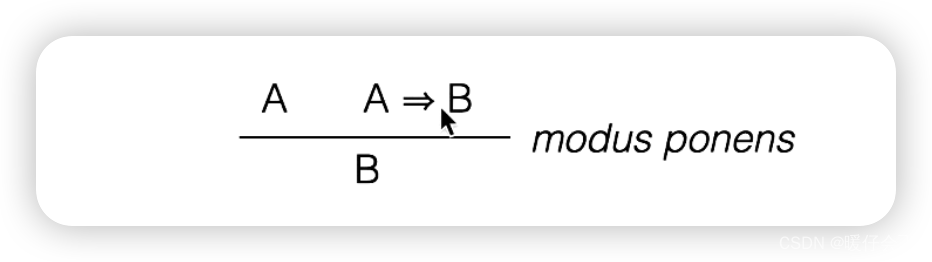
- 如果 A A A
holds(为true),同时 A = > B A=>B A=>B 也为 true,那么我们就能推导出 B B B 也为 true - “——” 代表 推导关系
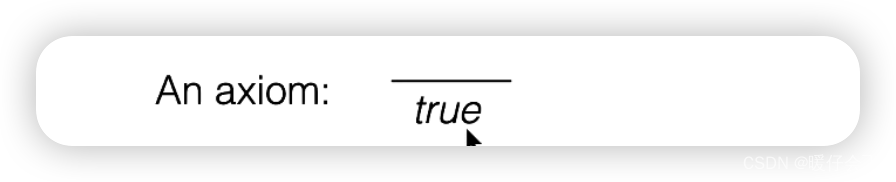
- 这个式子表明
true天生就holds - 也可以表示
我们假设这种情况是 true,因为不存在任何的前提条件,所以可以看成assumption
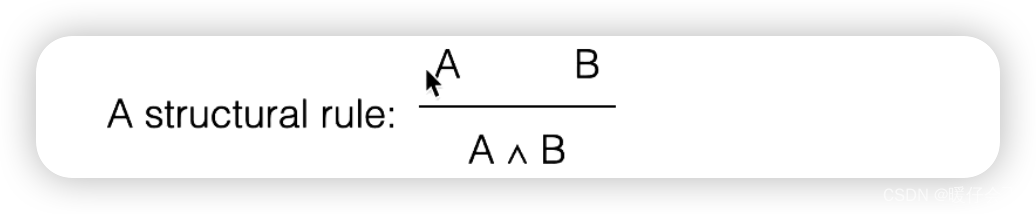
- 如果 A A A holds, 同时 B B B holds, 那么
A ^ B也 holds
forward v.s. backward
forward
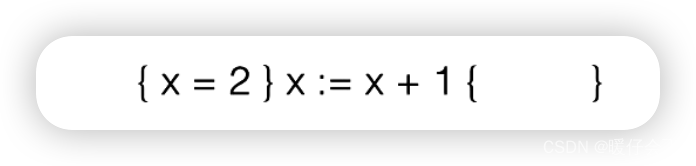
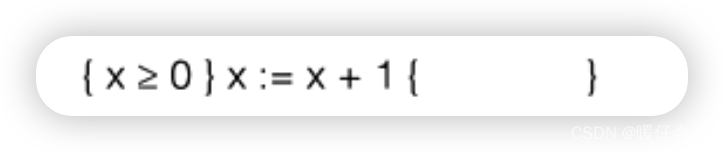
-
对于前面两个
forward推理还不困难
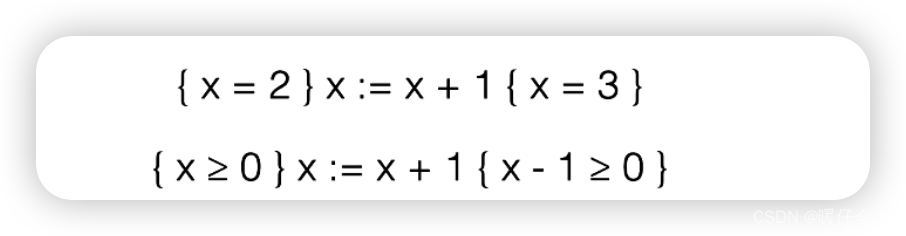
-
但是对于下面这个

backward
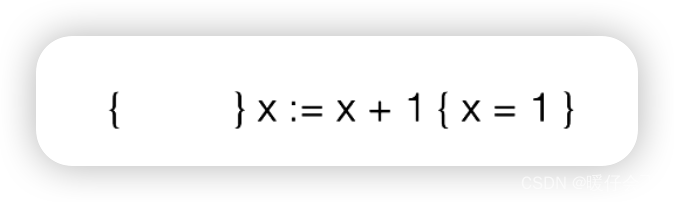
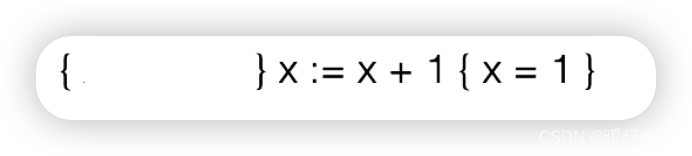
-
我们可以从
post的结果很容易推出pre的结果
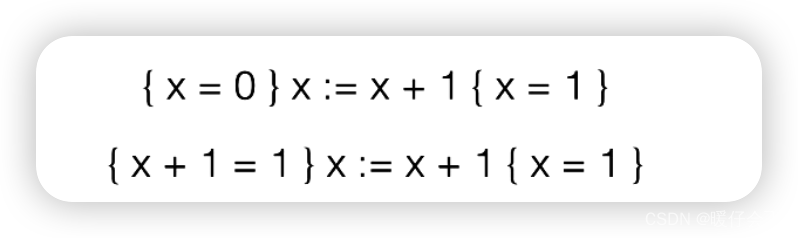
-
尤其是第二个式子,我们只需要根据结果
x=1和条件x:=x+1甚至不需要计算出来x=0我们只需要把x:=x+1的过程反过来就可以退出pre -
同样的:
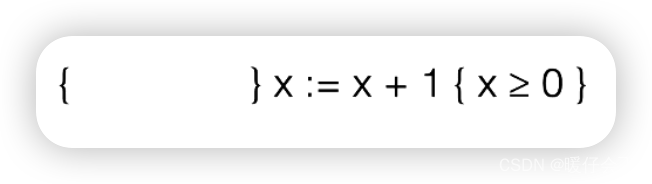
-
对于这个式子,我们也可以轻易的写出
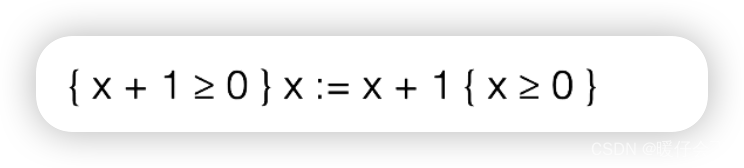
-
再看前面
forward推理很难的那个问题
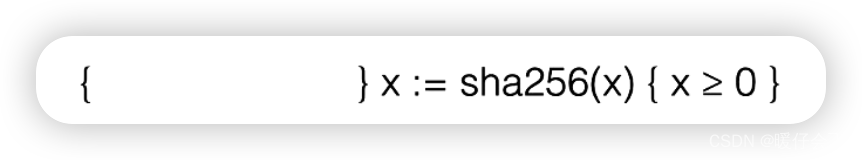
-
这里我们只需要
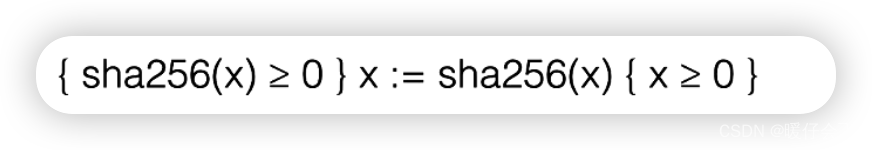
-
有上面的现象我们可以得到
rule of assignment
rule of assignment
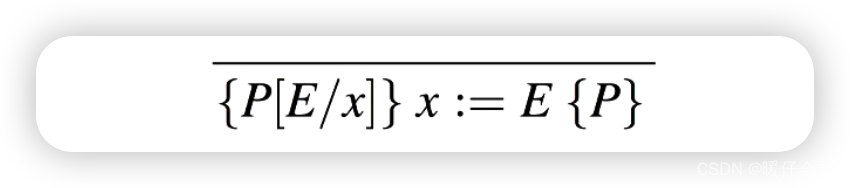
-
P P P 是关于 x x x 的公式,经过将
x:=E这个过程之后 P P P holds, -
那么我们把
post condition中的x全部用E来代替即可
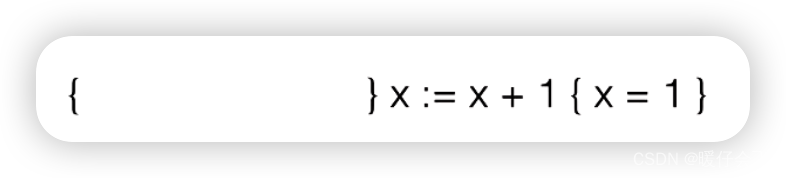
-
这个式子中 E = x + 1 E=x+1 E=x+1 所以把
post condition中的 x = 1 x=1 x=1 中的所有 x x x 替换成 E E E 作为precondition即 x + 1 = 1 x+1=1 x+1=1 -
所以结果就是:
{ x + 1 = 1 } x : = x + 1 { x = 1 } \{x+1=1\} x:=x+1\{x=1\} { x+1=1}x:=x+1{ x=1}
{ x = 0 } x : = x + 1 { x = 1 } \{x=0\}x:=x+1\{x=1\} { x=0}x:=x+1{ x=1} -
再练一个:
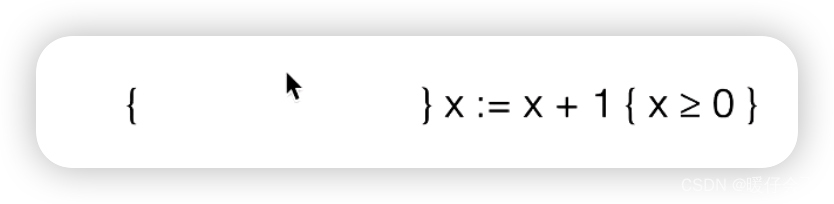
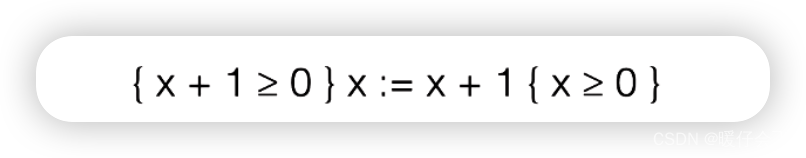
rules of consequence
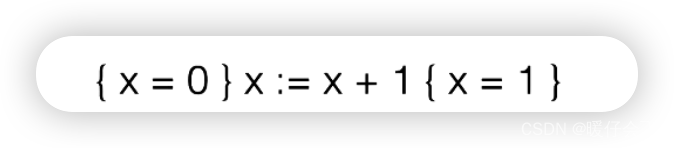
-
根据我们前面讨论的
forward和backward我们可以通过这个公式推导出:
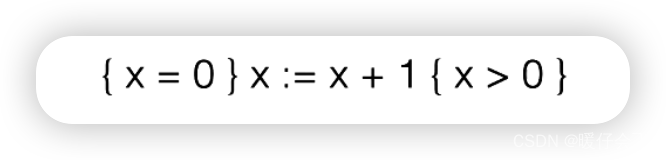
-
如果我们满足了下面的这种情况,我们同样能够得到
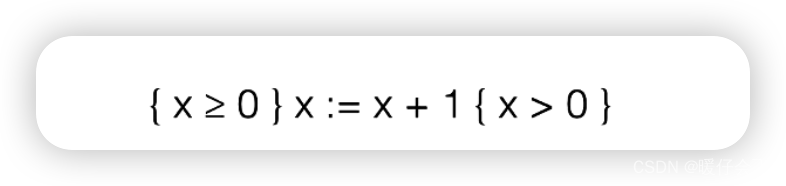
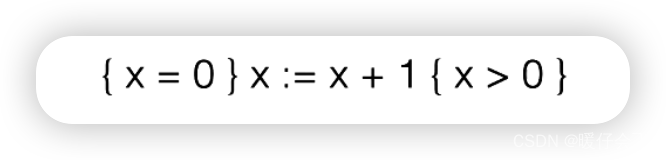
-
因为 x = 0 x=0 x=0 的条件比 x > = 0 x>=0 x>=0 要严格,因此作为
precondition也是可行的 -
由此
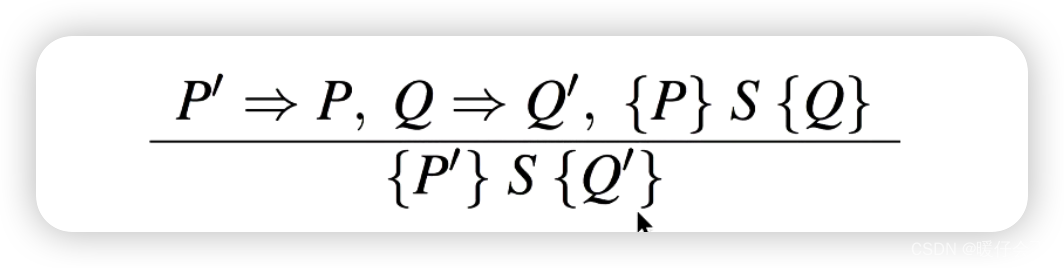
-
解析一下: P ′ P' P′ 是 P P P 的子集,同样的 Q Q Q 是 Q ′ Q' Q′ 的子集,因此 P P P 的范围要收窄,而 Q Q Q 的范围要扩大。
结合上述两个 rule
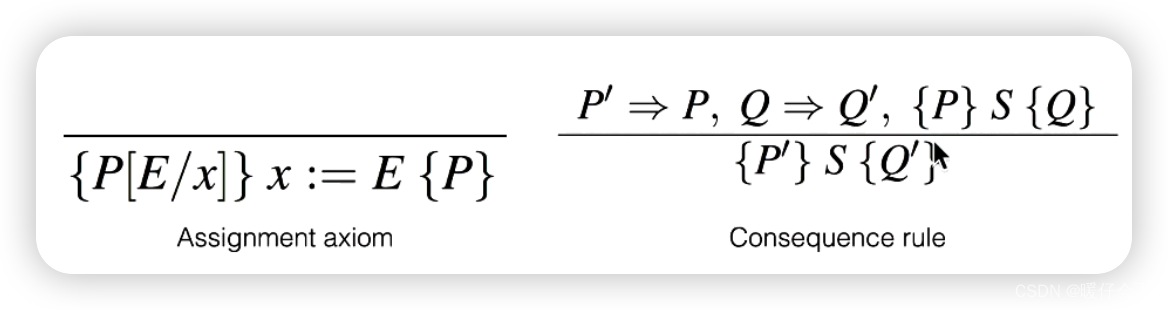
-
假设我们要证明:
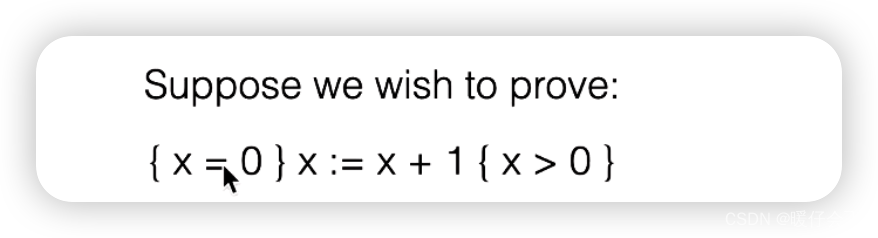
-
首先我们先把这个式子作为
consequence rule的下半部分,那么也就是 P ′ = { x = 0 } P'=\{x=0\} P′={ x=0}, Q ′ = { x > 0 } Q'=\{x>0\} Q′={ x>0}
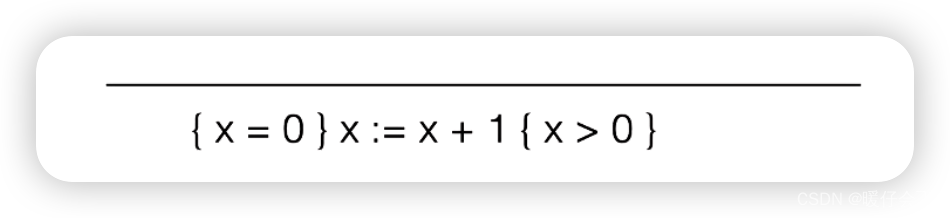
-
我们接下来不改变
post condition,当我们想使用consequence rule的时候我们需要找到 P ′ = > P P'=>P P′=>P ,而我们现在有 P ′ = { x = 0 } P' = \{x=0\} P′={ x=0} -
所以公式变成了下述:

-
假设有一个中间变量 P P P 是被推导出来的
-
接下来对下图中的红框中的部分使用
assignement axiom
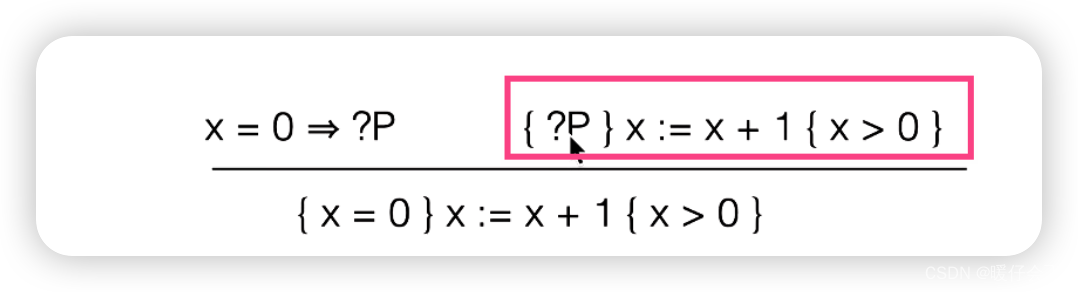
-
{ ? P } x : = x + 1 { x > 0 } \{?P\} x:=x+1 \{x>0\} { ?P}x:=x+1{ x>0} 可以推导出 P = x + 1 > 0 P=x+1>0 P=x+1>0
-
然后将这个带换到 x = 0 = > ? P x=0 => ?P x=0=>?P 的部分,就可以得到:
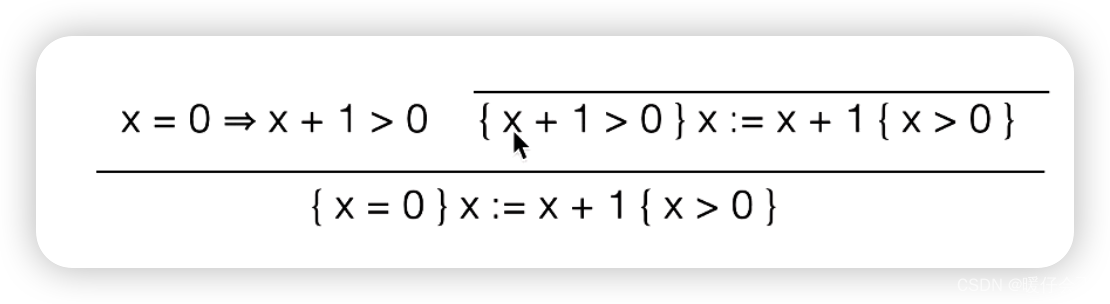
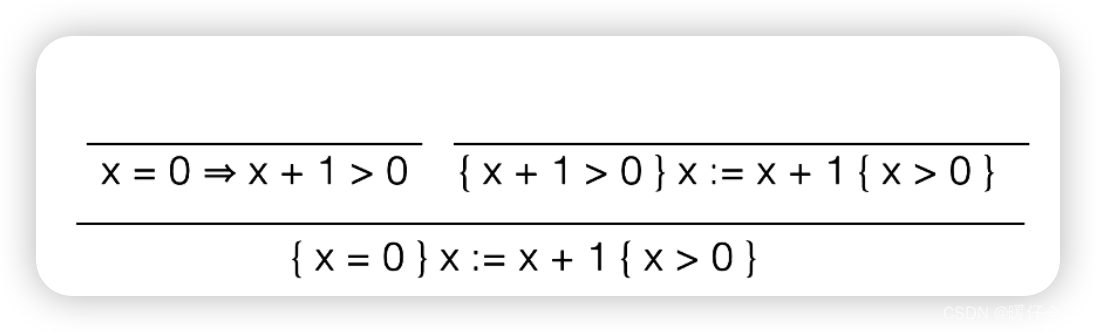
-
证明完成
-
总结以下上面的证明逻辑

rule of sequencing
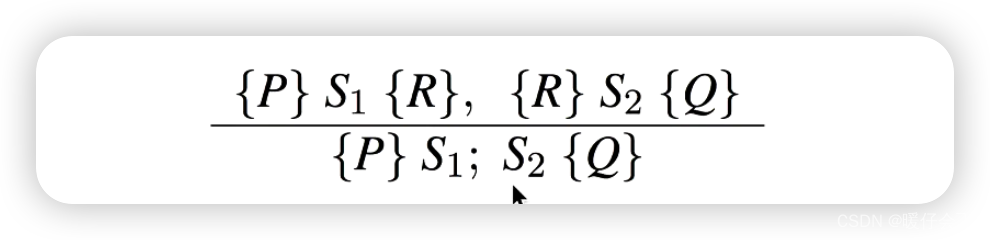
- 证明这一类题目的时候我们通常还是从后面一个部分开始,backward 的方式进行证明

- 证明开始:

- 证明开始:
- 首先利用
rule of consequence把 S 1 ; S 2 S1; S2 S1;S2 看成一个整体,此时 P ′ = { x = 0 } , Q ′ = { X = 2 } P'= \{x=0\}, Q'=\{X=2\} P′={ x=0},Q′={ X=2}所以这个时候我们还是需要看 P ′ = > P P'=>P P′=>P 所以我们还是假设有一个中间的变量 ? P ?P ?P
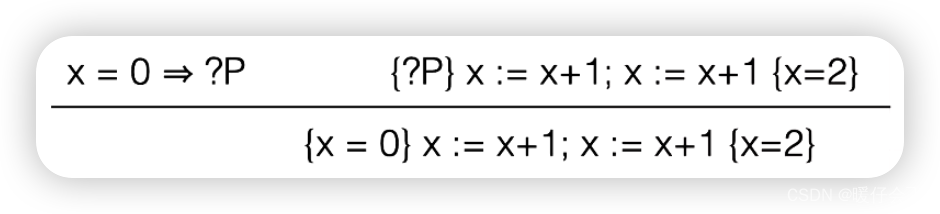
- 现在还不能对对下图中框选的部分进行
assign rule,因为assignment rule只能对single的步骤进行,因此我们现在要对下图中框选的部分进行rule of sequencing
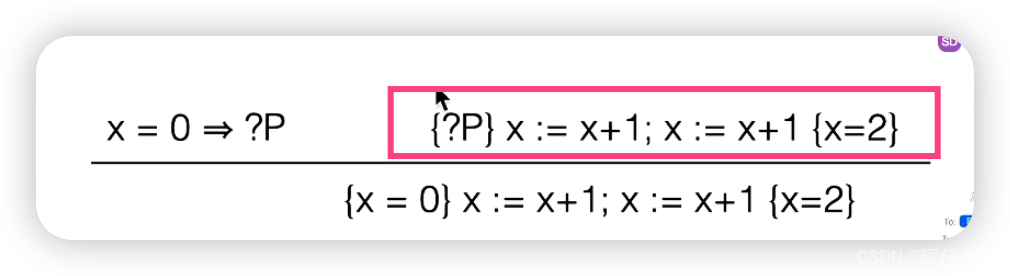
- 并得到:
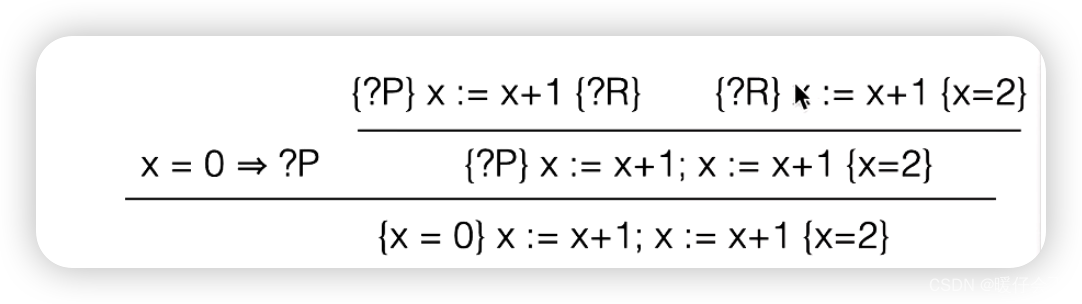
- 我们引入了一个中间变量 ? R ?R ?R,同时将中间推理拆分成两个
individual的部分 - 这个时候,请注意下图中框选的部分:

- 这里有两个未知的部分 ? P , ? R ?P, ?R ?P,?R 因此,我们要寻求别的突破口,其实也非常明显,我们可以从最后的那个式子的 ? R ?R ?R 开始使用
assignment rule

- 当这个证明出来之后,顺理成章对左上角包含 ? P ?P ?P 的式子再使用
assignment rule就可以了
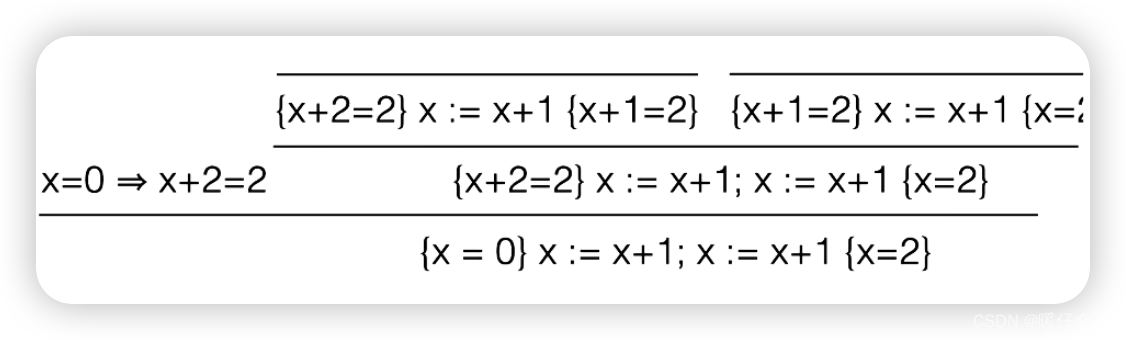
- 现在只剩下最左边的一部分了:

- 事实上他是恒成立的:
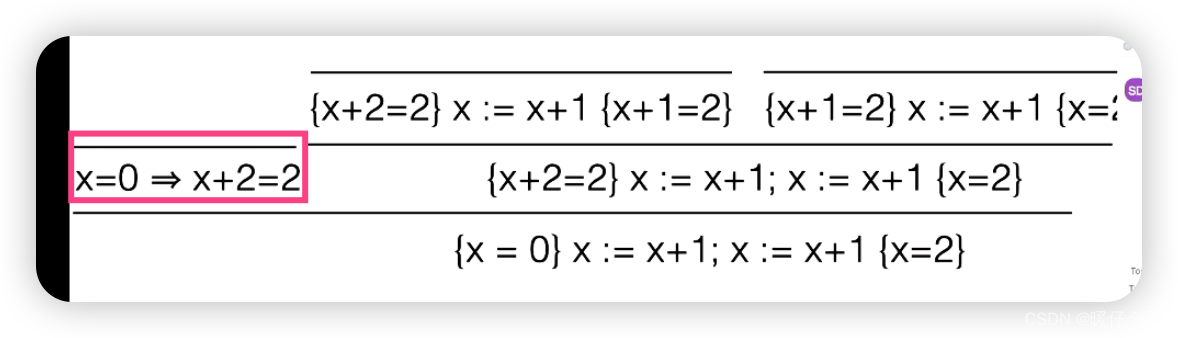
更大的程序案例
- 下列的程序表示的意思就是一个
swap程序
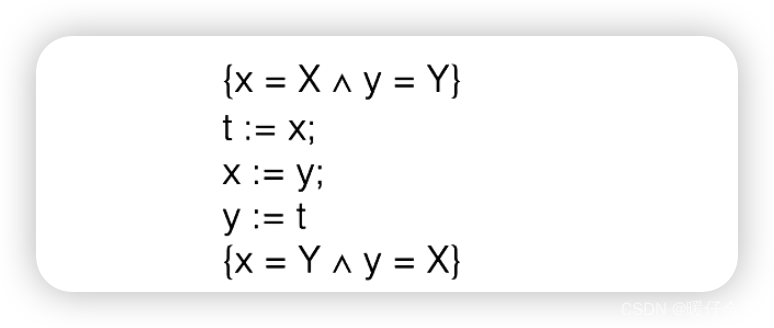


- 其实这个证明就相当于在每两个
s之间增加了一个中间项,然后需要逐一通过assignment rule来证明
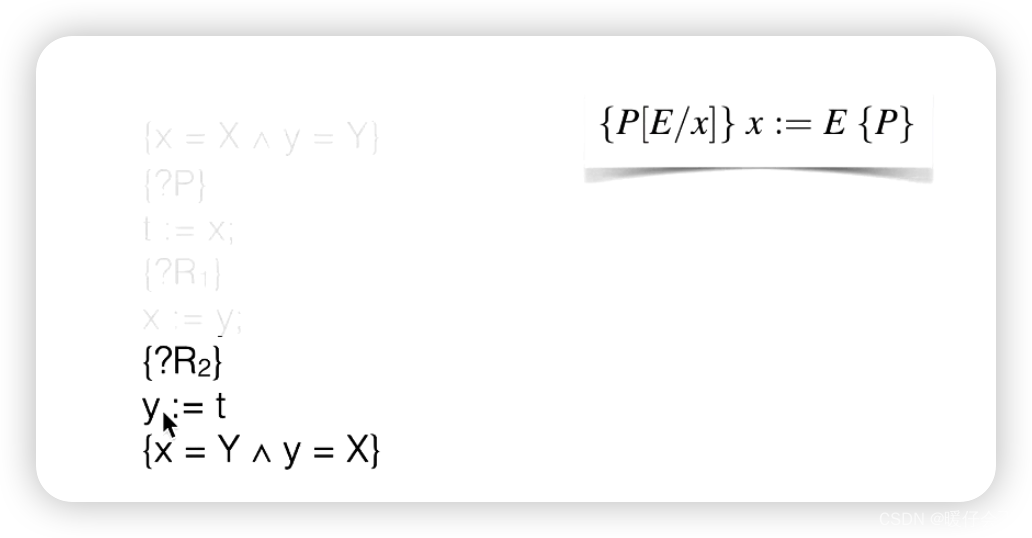


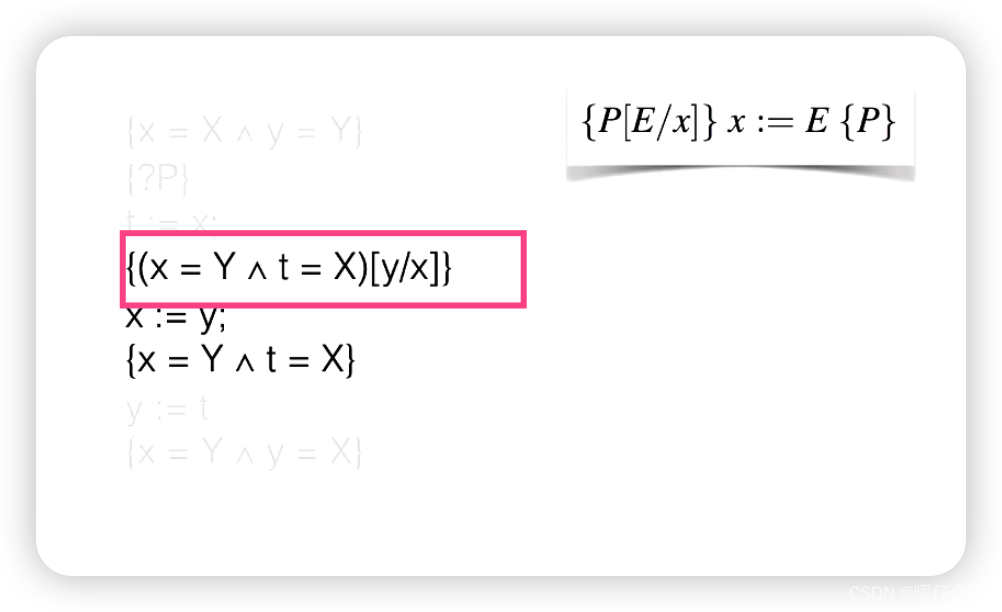


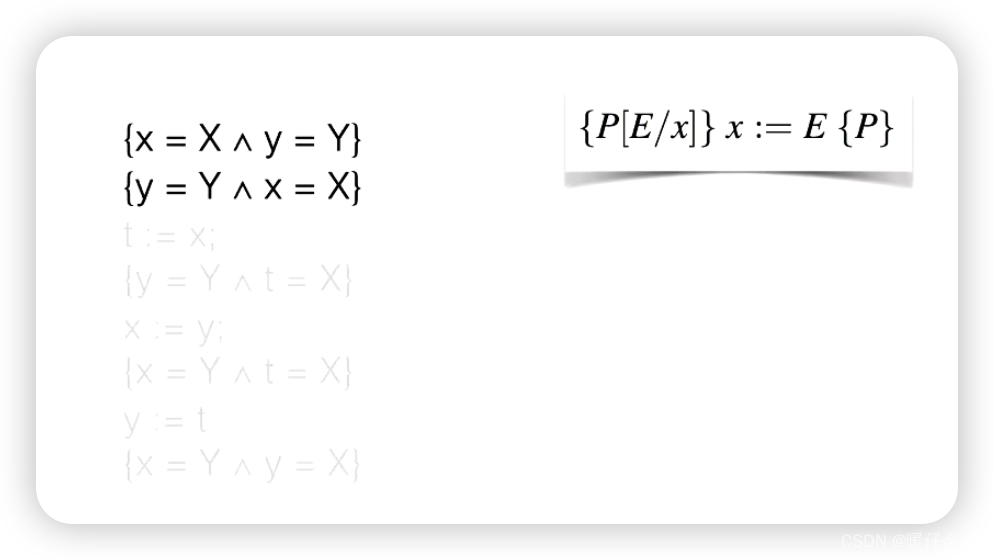
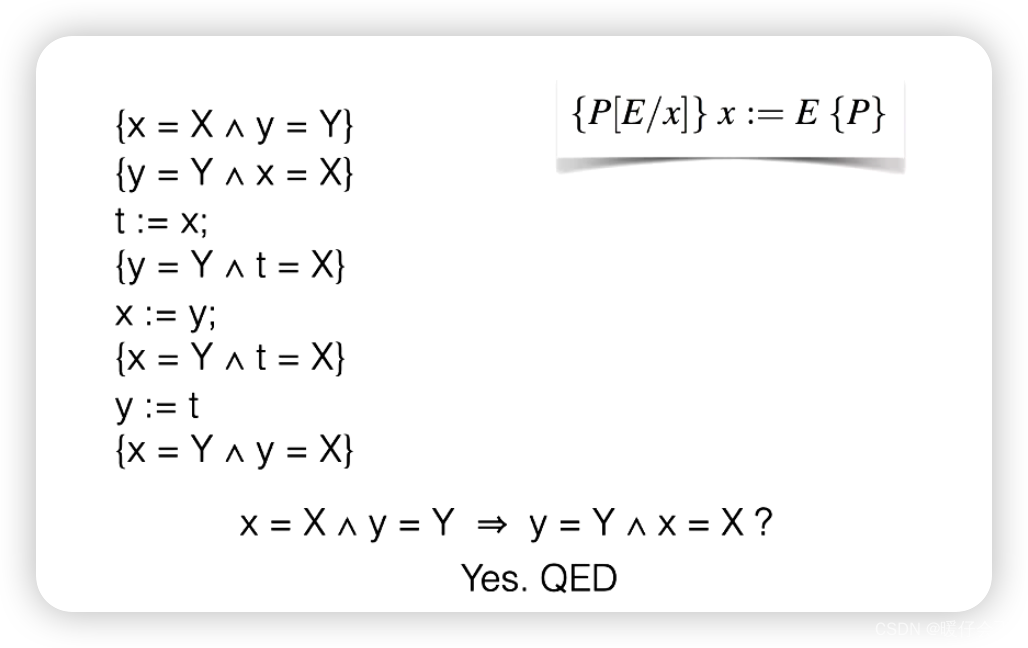
skip rule

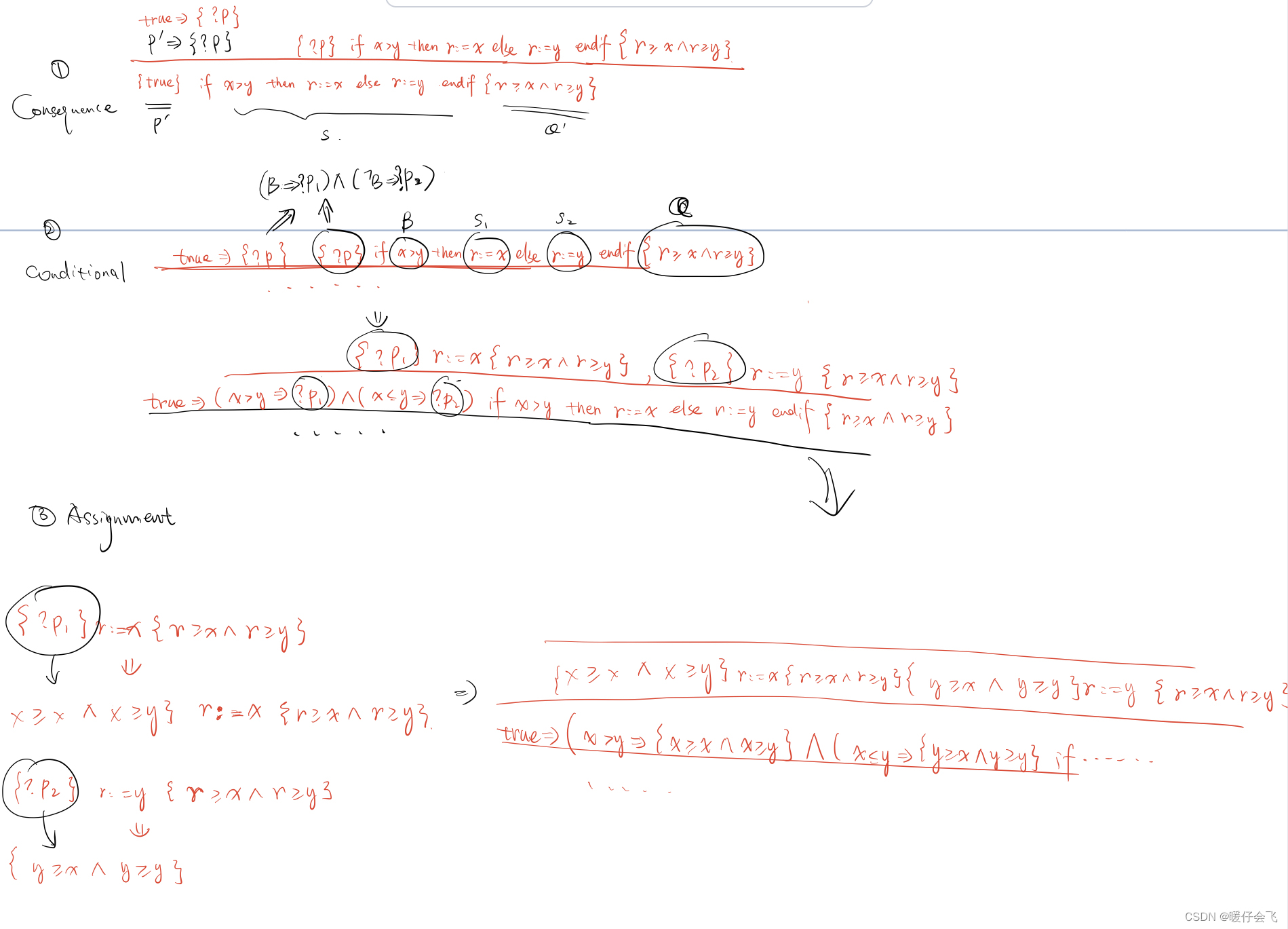
conditional rule
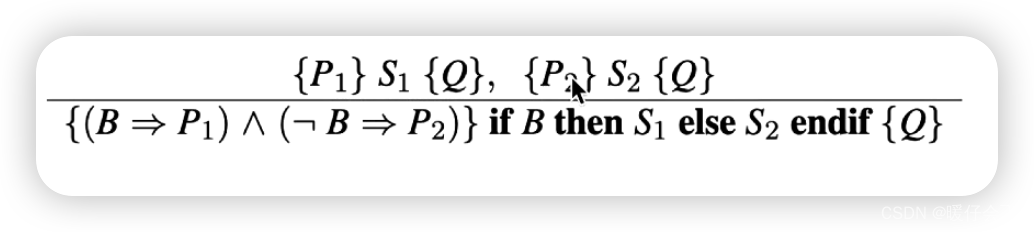
案例


- 还是首先使用
consequence rule - 这样我们就相当于在
precondition和 后续的运算之间加了个 ? P ?P ?P 
- 然后我们根据
conditional rule