1.认购期权与认沽期权
认购期权和认沽期权都是交易所常见的期权合约。
认购期权(Call Option)是一种给予持有人以在未来某个时间或特定事件发生时购买底层标的资产的权利。认购期权的持有人在行权日(Expiration Date)可以按照期权约定的价格(行权价格,也称执行价格)购买标的资产,也可以选择不行权。
认沽期权(Put Option)是一种给予持有人以在未来某个时间或特定事件发生时出售底层标的资产的权利。持有认沽期权的人可以在行权日按照期权约定的价格出售标的资产,或者选择不行权。
认购期权和认沽期权不同之处在于其行权时的行为。认购期权持有者在行权日可以根据行权价格购买标的资产,而认沽期权持有者则可以在行权日根据行权价格出售标的资产。
在期权交易中,持有认购期权的人利益与标的资产价格上涨相关;而持有认沽期权的人利益与标的资产价格下跌相关。认购和认沽期权的价格通常由许多因素影响,包括执行价格、到期日期、波动率、标的资产的价格等。
期权交易在投资者中非常受欢迎,因为它们为投资者提供了一个灵活的方式来参与市场,降低风险和锁定获利。然而,认购期权和认沽期权在实践中可以十分复杂,并涉及高度技术的分析和决策。投资者在进行期权交易时需要进行慎重的分析和评估,并确保了解所涉及的所有风险和成本。
2.欧式期权与美式期权
欧式期权是指持有人只能在到期日(或事先约定的某个日期)执行期权的权利。也就是说,欧式期权只有在到期日才能被行使。在此之前,持有人无法行使或出售该期权。
相比之下,美式期权给予持有人更大的灵活性。持有人在任何时间都可以选择行使该期权,无论是在到期日之前还是之后。这意味着,持有美式期权的人可以根据市场情况和个人利益来决定何时行使期权。
由于美式期权的灵活性,相对于欧式期权而言,它们通常会有更高的价值。因此,在相同的其他条件下,美式期权的价格通常会高于欧式期权。
无论是欧式期权还是美式期权,它们的定价都受到多种因素的影响,例如标的资产价格、行权价格、到期日、波动率、利率等。对于期权交易者和投资者来说,了解这些不同期权类型的特点和定价因素非常重要,以便根据自己的需求和风险偏好做出正确的决策。
3.计算欧式期权的杠杆率
首先介绍一下欧式期权的定价公式如下:
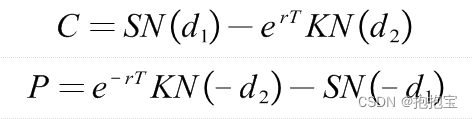
其中

其他 符号说明如下:
C :认购期权的价格
P:认沽期权的价格
S:标的物当前价格
K:行权价
r:无风险利率
T:到期时间
:标的物年华波动率
N():正太分布变量的累积分布函数
在上面的基础上,以认购期权为例,可以计算期权合约的杠杆率为

以某期权合约为例,期权价格C=0.3528,当日价格S=3.459,行权价格K=3.3,当日利率r=0.022284,合约到期日期t= 0.5,波动率sigma=0.2563,计算杠杆率的python代码如下:
import numpy as np
from scipy.stats import norm
def call_option_d(s,k,r,t,sigma):
d1 = (np.log(s / k) + (r + 0.5 * sigma * sigma) * t) / (sigma * np.sqrt(t))
d2 = d1 - sigma * np.sqrt(t)
return d1, d2
def call_option_lambda(s,k,r,t,sigma):
d1, d2 = call_option_d(s,k,r,t,sigma)
c = s * norm.cdf(d1) - np.exp(-r * t) * k * norm.cdf(d2)
lamb = norm.cdf(d1) * s / c
return lamb
sigma = 0.2563
t = 0.5
r = 0.022284
k = 3.3
s = 3.459
c = 0.3528
lamb = call_option_lambda(s,k,r,t,sigma)
print(lamb)
计算出杠杆率为6.4676。期权的杠杆率受很多因素的影响,可以利用控制变量法来体会杠杆率的变化。分别以到期时间1个月、2个月、3个月和6个月为例计算不同到期时间杠杆率随标的物现价的变化,并绘制变化图如下:
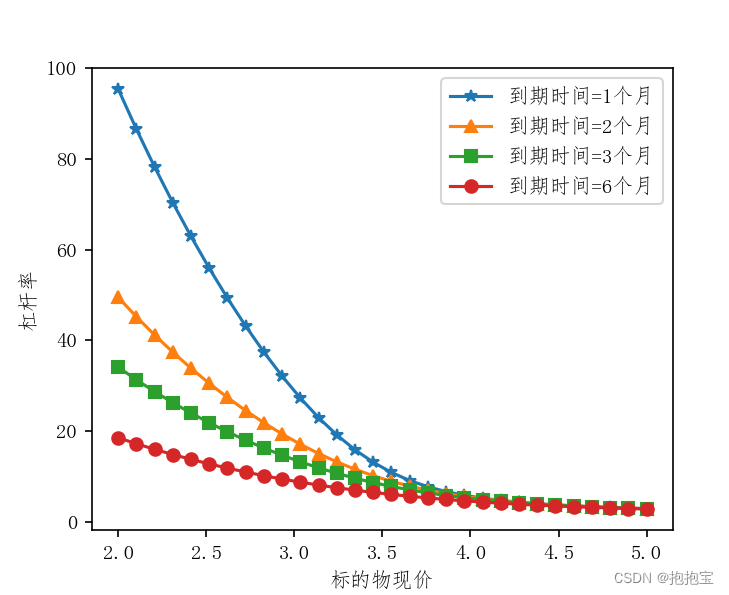
如图所示,可以看到随着到期时间的增加,杠杆率是逐渐变小的。对于认购期权来说,随着标的物价格增加,杠杆率会逐渐变小直至收敛到1。相反,随着标的物价格的减小,杠杆率会逐渐变大,理论上会到无穷大。但是,由于小单位的存在,虽然不会到无穷大,但也会是一个相当大的数字,因此,在交易期权时要格外小心,必须搞清楚合约的杠杆率以控制风险。
4.计算欧式期权的隐含波动率
事实上,波动率并不是通过统计方法得到的,而是由期权定价公式代入当前价格反解出来的隐含波动率。求隐含波动率,就等价于求一个方程的解。问题是这个方程没有简单的解析解,只能利用数值方法求解,这里使用二分法进行求解。
首先,虚拟一个看涨期权。其中,当前标的股价和执行价格都是10,利率是2%,到期时间是一年,波动率是20%。利用上节公式,可以求出它的理论价格为0.8916037278572535。
import numpy as np
from scipy.stats import norm
def bs(S, K, T, r, vol,c_p):
d1 = (np.log(S/K) + (r + 0.5*vol**2)*T) / (vol*np.sqrt(T))
d2 = d1 - vol * np.sqrt(T)
if c_p in ['C','c','Call','call','CALL']:
pv = S * norm.cdf(d1) - np.exp(-r * T) * K * norm.cdf(d2)
return pv
elif c_p in ['P','p','Put','put','PUT']:
pv = np.exp(-r * T) * K * norm.cdf(-d2) - S * norm.cdf(-d1)
return pv
else:
print('Wrong option type!')
return -1
S, K, T, r, vol, c_p = 10,10,1,0.02,0.2,'c'
pv = bs(S, K, T, r, vol,c_p)
print(pv)
然后设定一个波动空间,比如设定下届为0.1%,上届为1000%,分别代入公式求出对应的期权价格为-0.6935904609248063,9.108390596166512。
vol_0 = 0.001
vol_1 = 10
pv_0 = bs(S, K, T, r, vol_0,c_p)
print(pv_0 - pv)
pv_1 = bs(S, K, T, r, vol_1,c_p)
print(pv_1 - pv)最后利用二分法进行求解,设定设定求得的期权价格与理论价格之差的阈值为0.0001,当二者之差小于这个值时停止迭代,输出结果。
vol_0 = 0.001
vol_1 = 10
vol_x = (vol_0+vol_1)/2.0
pv_x = bs(S, K, T, r, vol_x,c_p)
tol = 0.0001
nn = 0
while (np.abs(pv_x - pv)>tol) and (nn<1000):
pv_x = bs(S, K, T, r, vol_x,c_p)
if pv_x < pv:
vol_0 = vol_x
vol_x = (vol_0+vol_1)/2.0
else:
vol_1 = vol_x
vol_x = (vol_0+vol_1)/2.0
nn += 1
print(nn,vol_x)
输出结果为:
1 2.50075
2 1.250875
3 0.6259374999999999
4 0.31346874999999996
5 0.15723437499999998
6 0.23535156249999997
7 0.19629296874999996
8 0.21582226562499995
9 0.20605761718749996
10 0.20117529296874997
11 0.19873413085937497
12 0.19995471191406247
13 0.20056500244140624
14 0.20025985717773437
15 0.20010728454589843
16 0.20003099822998044
17 0.19999285507202147
18 0.20001192665100095
经过18次迭代以后,得到的最终结果为20.012%,与真实值20%是非常接近的。