【数据结构】——6.4 AVL树
没有学过二叉搜索树(也叫二叉排序树或二叉查找树)的小伙伴们建议先学习一下,这样阅读会更轻松哦 点我学习二叉搜索树
目录
一、AVL树的概念
1. 二叉搜索树的问题
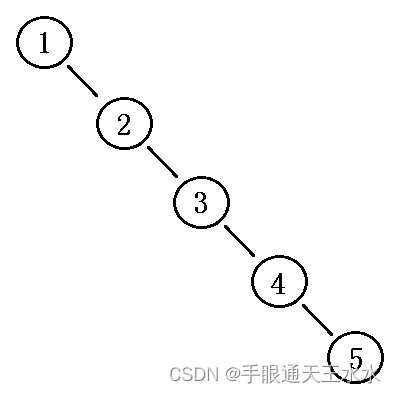
二叉搜索树的可以缩短查找的时间,提高查找效率。但是如果数据以接近有序的方式插入二叉搜索树中时,二叉搜索树将退化成一颗单支树,相当于在顺序表中查找元素,效率极低。
按照1 2 3 4 5的顺序插入的二叉搜索树如下:
2. AVL树的性质
为了解决这个问题,两个俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一个方法:如果保证每个节点的左右子树高度差的绝对值不超过1,即可以降低树的高度,减少平均搜索长度。
AVL树就是将二叉搜索树进行了平衡处理,避免了单支树带来查找效率上的降低。
- AVL树是一颗二叉搜索树。(空树也是AVL树)
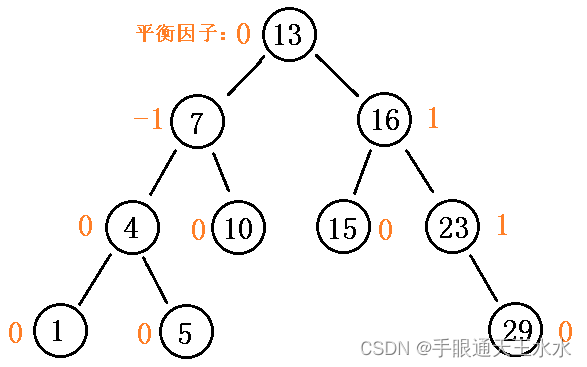
- AVL树的每个节点都引入了一个变量来记录它的左右子树的高度差,这个变量被称为平衡因子(balance factor)
- AVL树中的每个节点的平衡因子的绝对值不超过1,即左右子树的高度差的绝对值不超过1,只能是-1,0,1
- 一般情况下** 平衡因子 = 右子树高度 − 左子树高度 平衡因子 = 右子树高度-左子树高度 平衡因子=右子树高度−左子树高度**,但是也可以是 左子树高度 − 右子树高度 左子树高度-右子树高度 左子树高度−右子树高度。
二、AVL树实现平衡的方法
那如何实现让平衡因子保持绝对值不超过1呢?
- AVL树每次插入一个新节点时会更新平衡因子
- 通过平衡因子判断AVL树的平衡是否被破坏,若是没有被破坏,则不需要处理
- 若是平衡被破坏,则重新调整树的形状,使之依然保持平衡
1. 更新平衡因子
- 当一个AVL树每次插入新节点时,它的父节点的平衡因子都会更新
- 被插入的新节点是左孩子,则左子树高度变高,父节点的平衡因子-1;若为右孩子,则右子树会变高,父节点平衡因子+1。
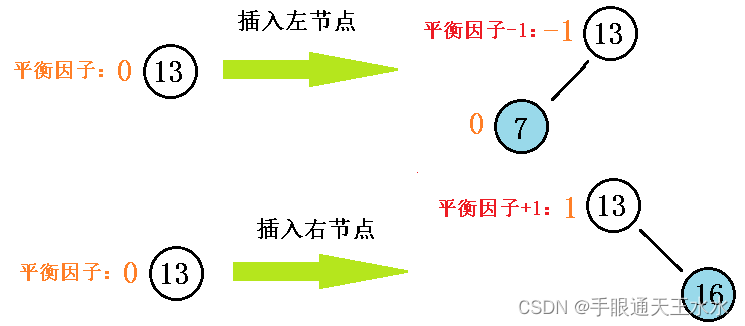
- 若是父节点的平衡因子更新后值为0,则证明插入的新节点没有影响它原有的高度,则不需要更新祖父节点的平衡因子

- 若是父节点平衡因子更新后值为-1或1,则证明它原来的平衡因子是0,而新插入的节点导致它的高度变高了,所以需要更新祖父节点的平衡因子。
- 若是父节点是祖父节点的左孩子,则祖父节点的平衡因子-1,若是右孩子,则祖父节点的平衡因子+1。
- 若是祖父节点的平衡因子更新后还是-1或1,则需要继续像上更新,直到平衡因子为0或其他值
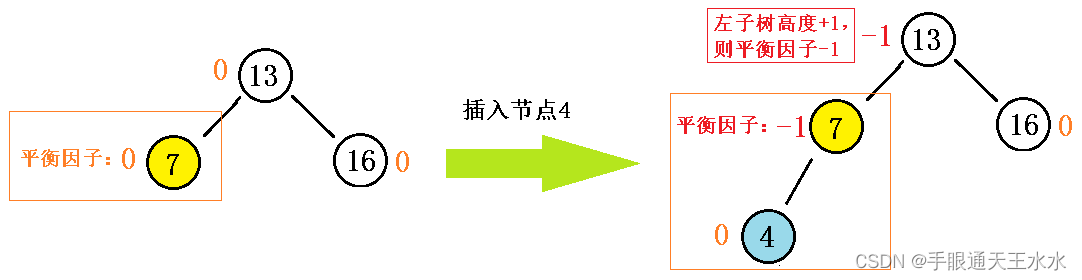
- 若是祖父节点更新后值为2或-2,则证明AVL树的平衡被破坏,需要对其进行调整

2. 破坏AVL树平衡的情况
AVL树平衡被破坏的情况有很多种,我们将其归为4类:
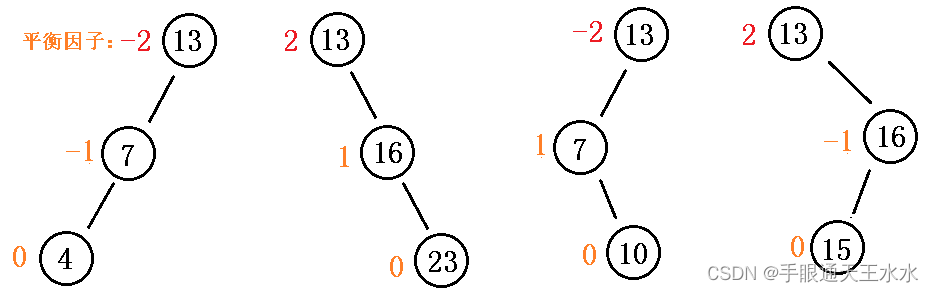
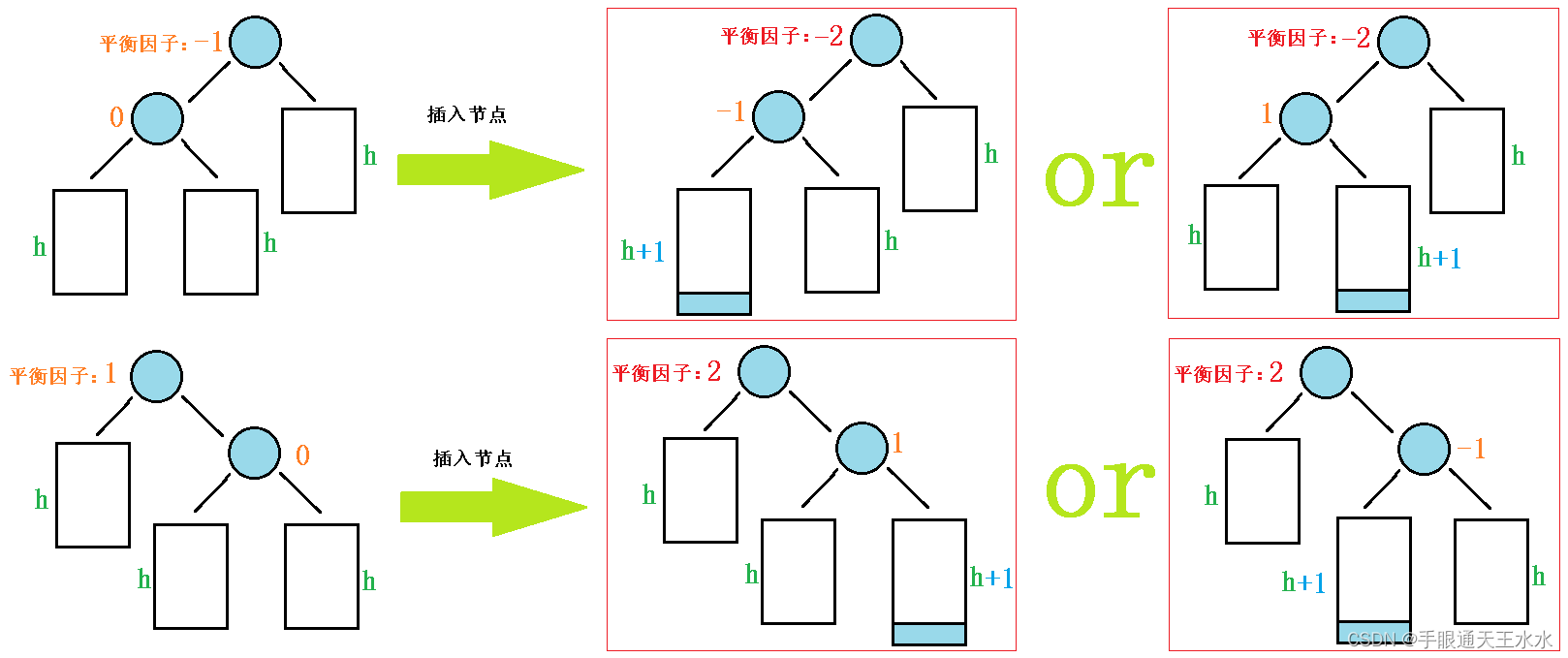
由于平衡因子可能更新过很多层才出现了-2或2,所以这导致平衡因子为2的节点的左右孩子未必是只有2个孩子的子树,所以我们用更为严谨的抽象图来表示这4种情况
图中的小方块是一颗高度为h的子树
3. AVL树的旋转
当AVL树的平衡被破坏时,我们通过对AVL树进行旋转来改变树的形状,以此来调整AVL树的平衡
这四种情况分别可以使用4种旋转方式将它们调整为平衡的二叉树:
3.1 右单旋
(1)旋转方法
当节点60和节点30的平衡因子为-2、-1时,出错的子树形状如下,它的调整方法是右单旋
- 让节点60成为节点30的右孩子
- 节点30原来的右孩子b子树成为节点60的左孩子
- 节点30和节点60的平衡因子更新为0
以上文字是对旋转过程的简述,对照下图的旋转过程食用更佳哦。
熟悉了一种旋转方式,对于后面的旋转方式可以对照图看,文字描述仅作参考辅助,不要只沉浸式地阅读这些枯燥的语句,画图更能帮助我们理解旋转过程
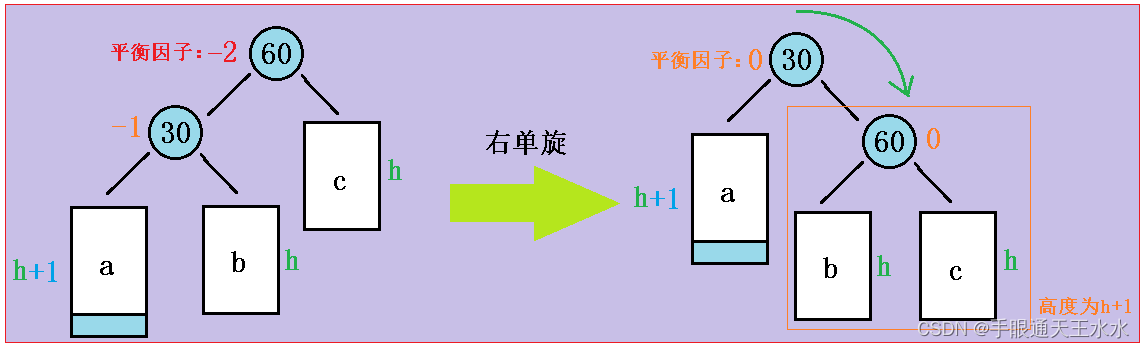
当我们旋转完毕后发现旋转后的高度和插入元素前的高度一样,所以旋转之后不用继续向上更新平衡因子了
(2)代码实现
- AVL树使用三叉链表来实现,所以需要更新父节点指针的指向
- 以节点30为轴右单旋,节点30由指针
cur指向,节点60由指针parent指向 - 当
cur指向的节点平衡因子为-2,parent指向的节点平衡因子为-1时,树形如图上所示,调用右单旋 - 右单旋完后将
cur和parent平衡因子更新为0
写代码小贴士:
- 创建指针变量分别指向当前节点、祖父节点、当前节点的右孩子。父节点作为参数被传递,不需要再创建变量。
- 链接节点时一定要看图
- 先链接每个节点的子节点,再更新每个节点的父节点。这样的方法会让我们书写代码时逻辑清晰一些,不容易造成混乱。
- 也可以按照节点进行链接,按照祖父节点、父节点、当前节点、当前节点的左孩子的顺序进行链接并更新父节点指针。
- 总之需要按照一定的逻辑顺序去链接,看到哪个链接哪个容易让我们遗漏链接过程,甚至造成内存泄漏。
// 节点的声明
struct Node
{
K _key; // key值
AVLTreeNode<K>* _left; // 左孩子指针
AVLTreeNode<K>* _right; // 右孩子指针
AVLTreeNode<K>* _parent; // 父节点指针
int _bf; // 平衡因子
};
// 测试函数
void test(void)
{
// ... ...
Node* parent; // 当前节点的父节点,指向图中的节点60
Node* cur; // 当前节点,指向图中的节点30
// ... ...
// 父节点平衡因子为-2,当前节点平衡因子为-1,调用右单旋
if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
}
// 右单旋
void RotateR(Node* parent)
{
Node* grandpa = parent->_parent; // 祖父节点,图中节点60的父节点
Node* cur = parent->_left; // 当前节点,图中的30节点
Node* subRight = cur->_right; // 当前节点的右孩子,图中的子树b
// 链接孩子节点
cur->_right = parent; // 链接当前节点的右孩子
parent->_left = subRight; // 链接父节点的左孩子
if (grandpa != nullptr) // 链接祖父节点的孩子
{
// 父节点不是根节点
if (grandpa->_left == parent)
{
grandpa->_left = cur;
}
else
{
grandpa->_right = cur;
}
}
else
{
// 父节节点是根节点
_root = cur;
}
// 更新父节点
cur->_parent = grandpa; // 更新当前节点的父节点指针
parent->_parent = cur; // 更新父节点的父节点指针
if (subRight != nullptr) // 更新当前节点左孩子的父节点指针
{
subRight->_parent = parent;
}
// 更新平衡因子
parent->_bf = cur->_bf = 0;
}
3.2 左单旋
(1)旋转方法
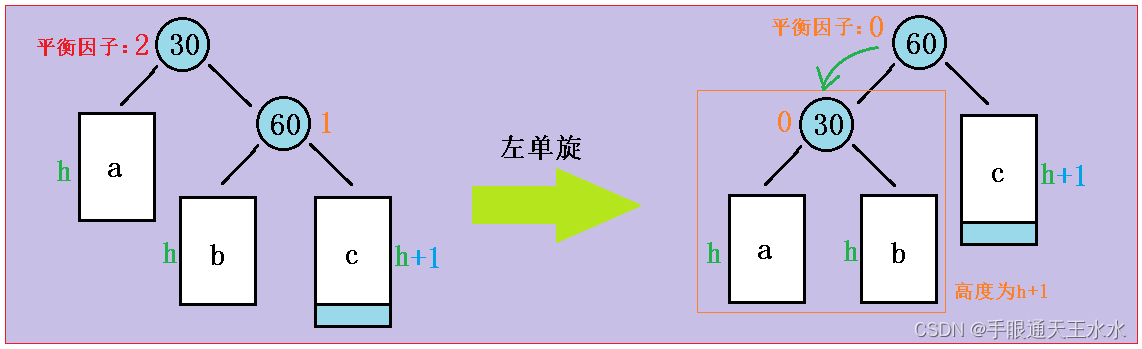
当节点30和节点60的平衡因子为2、1时,出错的子树形状如下,它的调整方法是左单旋
它的旋转方式与右单旋一样,只是方向相反
- 让节点30成为节点60的左孩子
- 节点60原来的左孩子b子树成为节点30的右孩子
- 节点30和节点60的平衡因子更新为0
(2)代码实现
实现方法与右单旋一样,只是方向相反
- 以节点60为轴左单旋,节点60由指针
cur指向,节点30由指针parent指向 - 当
cur指向的节点平衡因子为2,parent指向的节点平衡因子为1时,树形如图上所示,调用左单旋 - 左单旋完后将
cur和parent平衡因子更新为0
// 测试函数
void test(void)
{
// ... ...
Node* parent; // 当前节点的父节点,指向图中的节点30
Node* cur; // 当前节点,指向图中的节点60
// ... ...
// 父节点平衡因子为2,当前节点平衡因子为1,调用左单旋
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
}
// 左单旋
void RotateL(Node* parent)
{
Node* grandpa = parent->_parent;
Node* cur = parent->_right;
Node* subLeft = cur->_left;
// 链接孩子节点
cur->_left = parent;
parent->_right = subLeft;
if (grandpa != nullptr)
{
if (grandpa->_left == parent)
{
grandpa->_left = cur;
}
else
{
grandpa->_right = cur;
}
}
else
{
_root = cur;
}
// 更新父节点
cur->_parent = grandpa;
parent->_parent = cur;
if (subLeft != nullptr)
{
subLeft->_parent = parent;
}
// 更新平衡因子
parent->_bf = cur->_bf = 0;
}
3.3 左右双旋
由于以上的抽象图无法清晰的描述AVL树的旋转过程,所以我们将以下图中红色方框里的子树b展开一层:
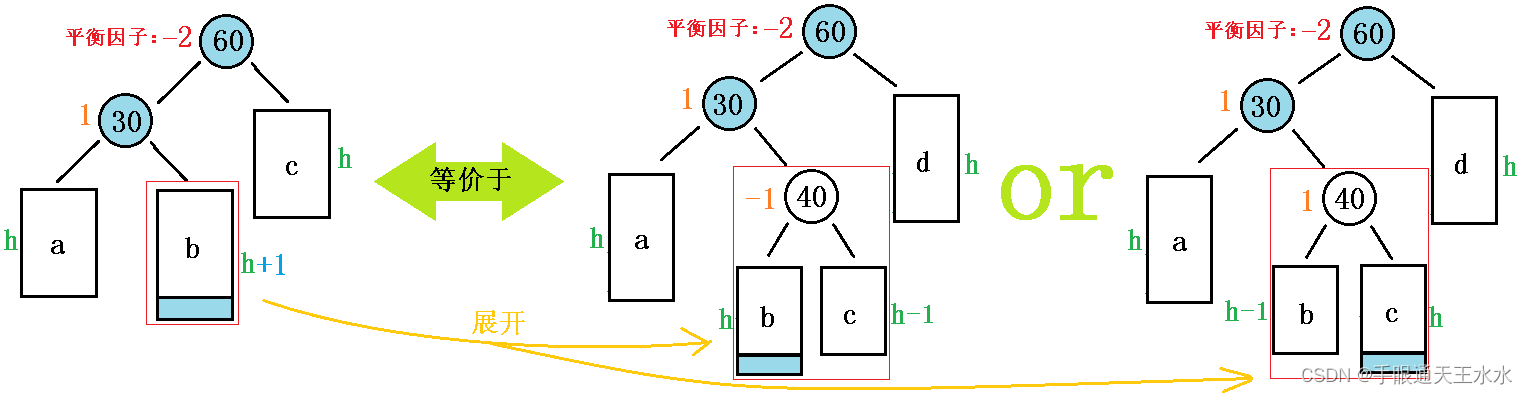
(1)旋转方法
这个过程有2个旋转步骤,先左单旋,再右单旋。因此也叫左右双旋
- 以节点40为轴进行左单旋:
- 让节点30成为节点40的左孩子
- 节点40原来的左孩子b子树成为节点30的右孩子
- 让旋转后的树成为节点60的左孩子,即让节点40成为节点60的右孩子
- 此处可以不用更新平衡因子,到下一步右单旋完成后,之间将平衡因子更新到最终结果的值
- 以节点40为轴进行右单旋:
- 让节点60成为节点40的右孩子
- 节点40原来的右孩子c子树成为节点60的左孩子
- 更新平衡因子:
- 最后结果中的平衡因子不再是一成不变的0了,而是要分情况讨论了。我们要根据节点40的平衡因子来判断新节点是插入在节点40的左子树还是右子树
- 若是节点40的平衡因子是-1,则新节点插入在左子树,树的形状如下图左边所示。要将节点60的平衡因子更新为1
- 若是节点40的平衡因子是1,则新节点插入在右子树,树的形状如下图右边所示。要将节点30的平衡因子更新为-1
- 若是节点40的平衡因子是0,则自己就是新节点,所有节点的平衡因子都是0了
- 最后将剩下两个节点的平衡因子全部更新为0
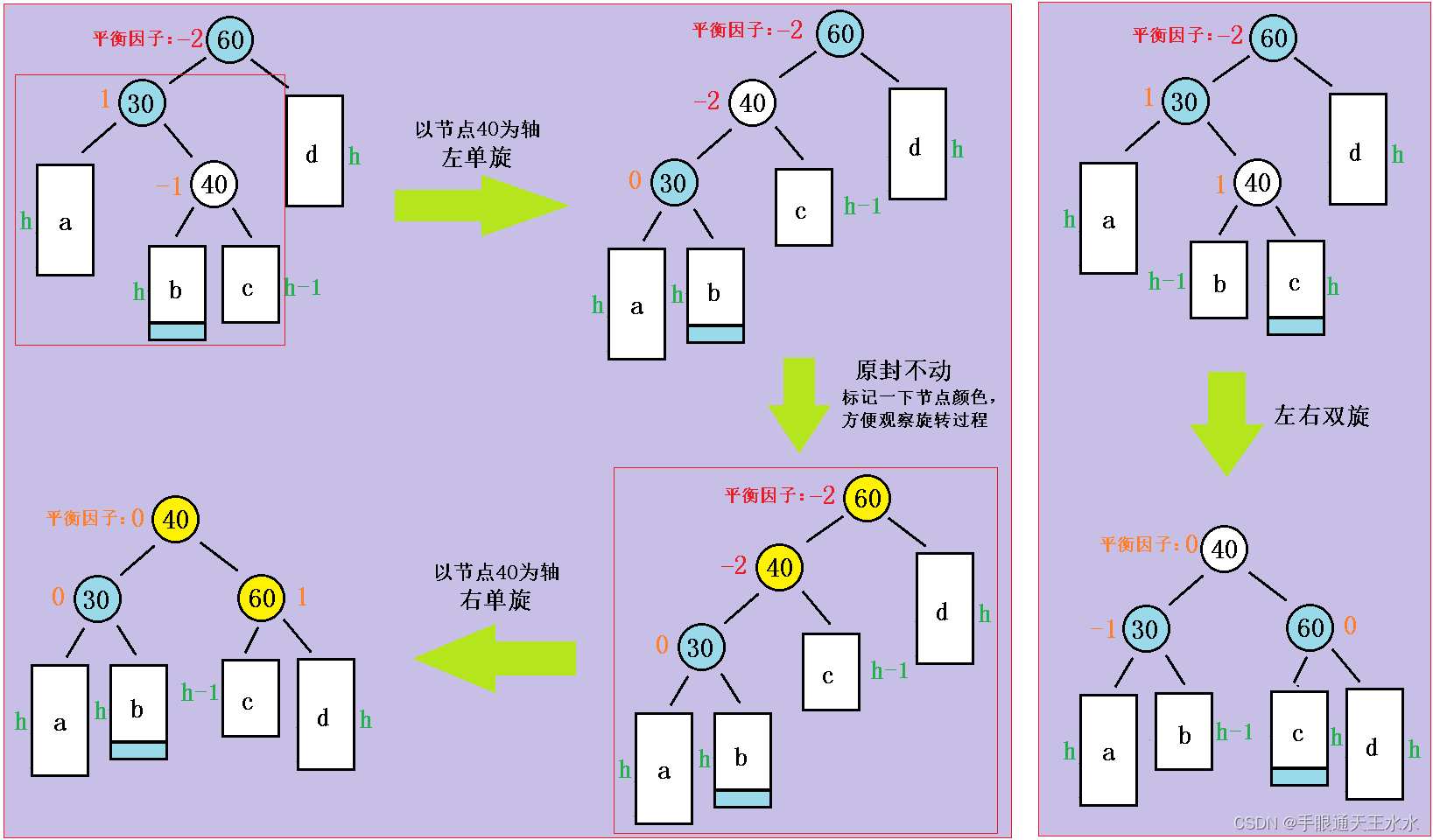
(2)代码实现
- 节点30由指针
cur指向,节点60由指针parent指向。 - 当
parent节点平衡因子为-2,cur节点平衡因子为1时,调用左右双旋。(先负后正 即 先左后右) - 由于左单旋和右单旋我们已经实现,直接调用即可,但是要传入不同的参数
- 在旋转之前要提前记录图中节点40位置的平衡因子,并为之更新平衡因子
// 测试函数
void test(void)
{
// ... ...
Node* parent; // 当前节点的父节点,指向图中的节点60
Node* cur; // 当前节点,指向图中的节点30
// ... ...
// 父节点平衡因子为-2,当前节点平衡因子为1,调用左右双旋
if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
}
// 左右双旋
void RotateLR(Node* parent)
{
Node* cur = parent->_left; // 当前节点,指向图中的节点30
Node* subRight = cur->_right; // 当前节点的子节点,指向图中的节点40
int bf = subRight->_bf; // 记录图中节点40的平衡因子
// 左右双旋
RotateL(cur); // 以subRight为轴左单旋(参数传递的是轴的父节点)
PotateR(parent); // 以cur为轴右单旋
// 更新平衡因子
if (bf == -1) // subRight左子树新增
{
parent->_bf = 1;
cur->_bf = 0;
subRight->_bf = 0;
}
else if (bf == 1) // subRight右子树新增
{
cur->_bf = -1;
parent->_bf = 0;
subRight = 0;
}
else if (bf == 0) // subRight自己就是新增
{
parent->_bf = 0;
cur->_bf = 0;
subRight->_bf = 0;
}
else // 平衡因子出现其他情况,不可能发生,断言处理
{
assert(false);
}
}
3.4 右左双旋
和左右双旋一样,我们依然将子树b展开一层:
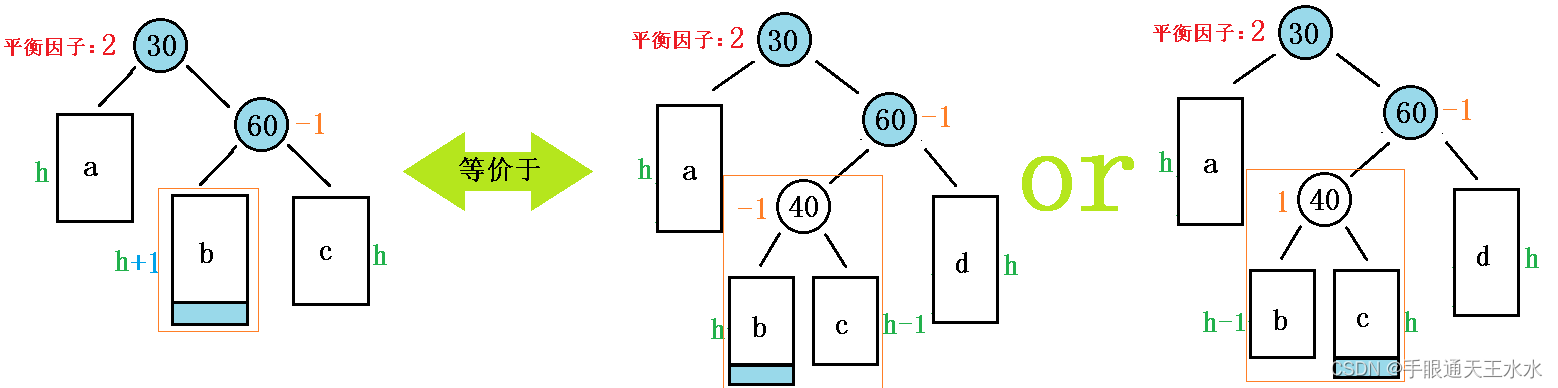
(1)旋转方法
这个过程有2个旋转步骤,先右单旋再左单旋,叫右左双旋:
- 以节点40为轴进行右单旋:
- 让节点60成为节点40的右孩子
- 节点40原来的左孩子b子树成为节点60的左孩子
- 让旋转后的树成为节点30的左孩子,即让节点40成为节点30的右孩子
- 此处可以不用更新平衡因子,到下一步右单旋完成后,之间将平衡因子更新到最终结果的值
- 以节点40为轴进行左单旋:
- 让节点30成为节点40的左孩子
- 节点40原来的右孩子c子树成为节点30的左孩子
- 更新平衡因子:
- 平衡因子与左右双旋一样,也要分情况讨论。
- 若是节点40的平衡因子是-1,则新节点插入在左子树,树的形状如下图左边所示。要将节点60的平衡因子更新为1
- 若是节点40的平衡因子是1,则新节点插入在右子树,树的形状如下图右边所示。要将节点30的平衡因子更新为-1
- 若是节点40的平衡因子是0,则自己就是新节点,所有节点的平衡因子都是0了
- 最后将剩下两个节点的平衡因子全部更新为0
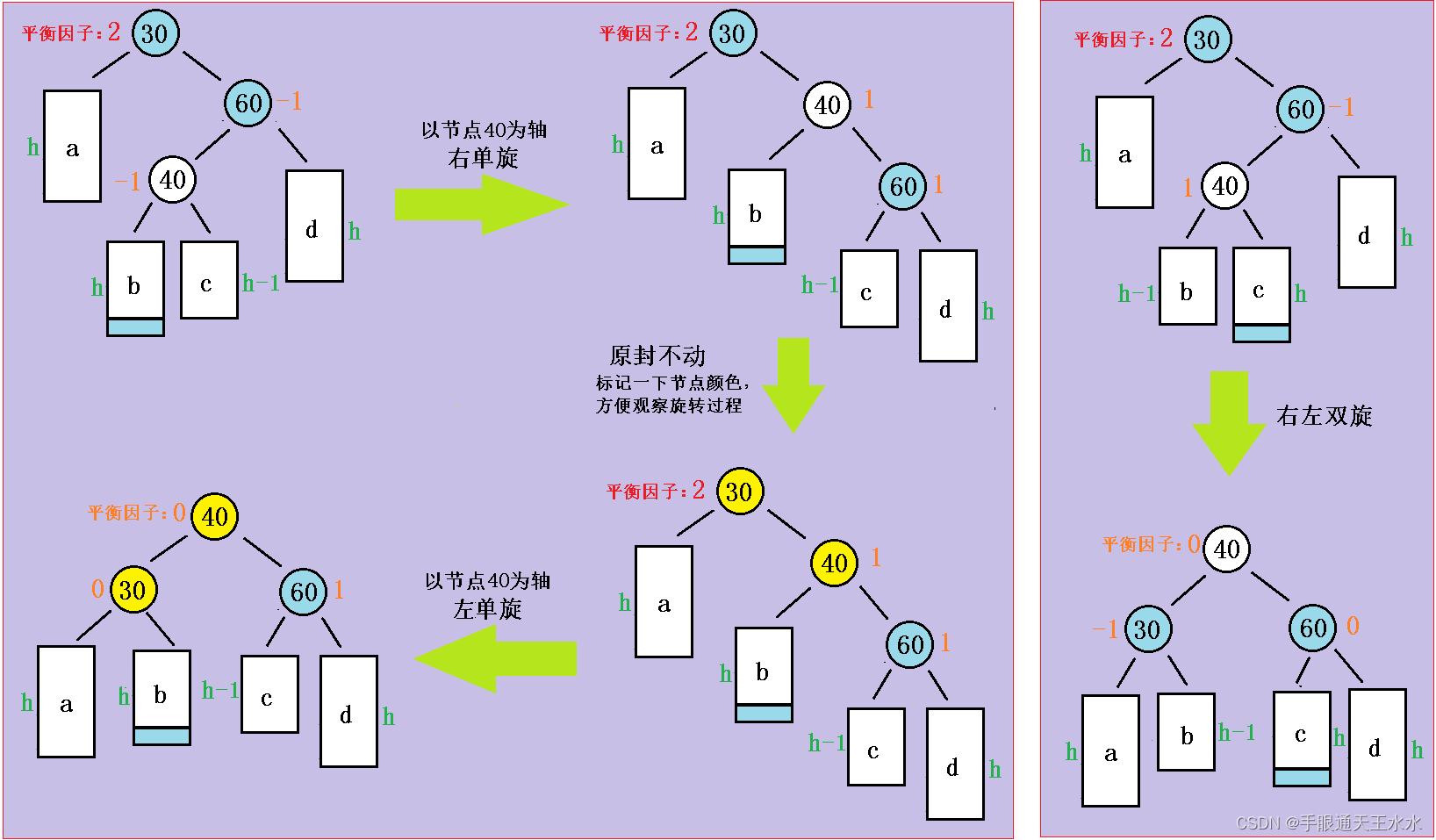
(2)代码实现
与左右双旋一样,只是方向相反
// 测试函数
void test(void)
{
// ... ...
Node* parent; // 当前节点的父节点,指向图中的节点30
Node* cur; // 当前节点,指向图中的节点60
// ... ...
// 父节点平衡因子为2,当前节点平衡因子为-1,调用右左双旋
if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
}
// 右左双旋
void RotateRL(Node* parent)
{
Node* cur = parent->_right;
Node* subLeft = cur->_left;
int bf = subLeft->_bf;
// 右左双旋
RotateR(cur);
RotateL(parent);
// 更新平衡因子
if (bf == -1) // subLeft左子树新增
{
cur->_bf = 1;
parent->_bf = 0;
subLeft->_bf = 0;
}
else if (bf == 1) // subLeft右子树新增
{
parent->_bf = -1;
cur->_bf = 0;
subLeft = 0;
}
else if (bf == 0) // subLeft自己就是新增
{
parent->_bf = 0;
cur->_bf = 0;
subLeft->_bf = 0;
}
else
{
assert(false);
}
}
三、AVL树的实现
1. 存储结构和接口
AVL树是一个搜索二叉树,我们使用三叉链表来实现。(即每个节点有左右孩子指针外,还有一个指针指向它的父节点)
每个节点中有一个整型变量表示平衡因子
AVL树中我们需要实现的接口如下代码所示:
节点的删除比较复杂,不做实现。我们还会写一个测试函数IsBalance,来检测我们的AVL树是否满足规则
namespace wh
{
// AVL树的节点
template <class K>
struct AVLTreeNode
{
K _key; // key值
AVLTreeNode<K>* _left; // 左孩子指针
AVLTreeNode<K>* _right; // 右孩子指针
AVLTreeNode<K>* _parent; // 父节点指针
int _bf; // 平衡因子
// 构造函数
AVLTreeNode(const K& key)
: _key(key)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
{
;
}
};
// AVL树
template <class K>
class AVLTree
{
typedef AVLTreeNode<K> Node; // 声明节点类型为Node
public:
// 需要实现的接口(不含默认成员函数)
bool Insert(const K& key); // 插入
bool Find(const K& key); // 查找
bool InOrder(void); // 中序遍历
bool IsBalance(void); // 检查是否平衡,测试自己实现的AVL树是否满足规律
private:
Node* _root; // 根节点指针
};
}
2. 默认成员函数的实现
(1)构造函数
初始化根节点指针为nullptr
AVLTree(void)
: _root(nullptr)
{
;
}
(2)析构函数
与普通搜索二叉树一样,后序遍历,一个一个释放节点
// 析构函数
~AVLTree(void)
{
_Destroy(_root);
_root = nullptr;
}
private:
// 后序遍历释放节点
void _Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
(3)拷贝构造
与普通搜索二叉树一样,先序遍历,拷贝内容
// 拷贝构造
AVLTree(const AVLTree& t)
{
_root = _Copy(_root, t._root);
}
private:
// 先序遍历递归拷贝节点
Node* _Copy(Node* root, const Node* src)
{
if (src == nullptr)
{
return nullptr;
}
root = new Node(src->_key);
root->_left = _Copy(root->_left, src->_left);
root->_right = _Copy(root->_right, src->_right);
return root;
}
(4)赋值重载
创建临时变量复制被拷贝的AVL树,然后交换二者的根节点内容
// 赋值重载函数
AVLTree& operator=(const AVLTree& t)
{
if (this != &t)
{
BSTree temp(t);
std::swap(temp._root, _root);
}
return *this;
}
3. 插入元素
- 插入:
- 按照搜索二叉树的规则插入新节点
- 更新平衡因子:
- 从下到上更新平衡因子,直到平衡因子被更新为0、2或-2
- 当平衡因子被更新到0时,则AVL树平衡没被破坏,插入结束
- 旋转:
- 若是平衡因子被更新到2或-2时,平衡被破坏。
- 根据平衡因子判读被破坏时的树的形状,对其进行旋转
- 最后更新旋转后的平衡因子
- 旋转之后子树的高度与插入之前的子树高度一样,不用向上继续更新平衡因子了,插入
代码如下:
bool Insert(const K& key)
{
// 1.插入新节点
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root, parent = nullptr;
while (cur != nullptr)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(key);
cur->_parent = parent;
if (key < parent->_key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
// 2.更新平衡因子
while (parent != nullptr)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
{
// 平衡因子更新到0,不作处理
break;
}
else if (parent->_bf == -1 || parent->_bf == 1)
{
// 让平衡因子继续更新
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == -2 || parent->_bf == 2)
{
// 3.平衡被破坏,旋转
if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent); // 右单旋
}
else if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent); // 左单旋
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent); // 左右双旋
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent); // 右左双旋
}
else
{
assert(false);
}
break; // 旋转完毕后插入结束
}
else
{
// 平衡因子是其他值,理论上不可能出现,使用断言处理
assert(false);
}
}
}
4. 查找元素
查找方式与二叉搜索树一样
bool Find(const K& key)
{
Node* cur = _root;
while (cur != nullptr)
{
if (key < cur->_key)
{
// 比当前节点小,往左走
cur = cur->_left;
}
else if (key > cur->_key)
{
// 比当前节点大,往右走
cur = cur->_right;
}
else
{
// 与当前节点相等,返回true
return true;
}
}
return false;
}
5. 中序遍历
递归实现中序遍历
// 中序遍历
void InOrder(void)
{
_InOrder(_root);
std::cout << std::endl;
}
// 中序遍历的递归过程
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
std::cout << root->_key << " ";
_InOrder(root->_right);
}
6. 检测是否为AVL树
通过遍历节点,判断每个节点的平衡因子是否为左右子树的高度差,以及平衡因子的绝对值是否超过1
// 检查是否为AVL树
bool IsBalance(void)
{
return _IsBalance(_root);
}
private:
// 递归检测每个节点是否满足AVL树的条件
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int left = _GetHigh(root->_left);
int right = _GetHigh(root->_right);
int bf = right - left;
if (bf != root->_bf || bf > 1 || bf < -1)
{
return false;
}
return _IsBalance(root->_left) && _IsBalance(root->_right);
}
// 获取二叉树的高度
int _GetHigh(Node* root)
{
if (root == nullptr)
{
return 0;
}
int left = _GetHigh(root->_left);
int right = _GetHigh(root->_right);
return (left > right ? left : right) + 1;
}
测试样例演示:
#include <iostream>
#include <cstdlib>
#include <ctime>
void test(void)
{
srand((unsigned)time(nullptr));
Name::AVLTree<int> t;
// 插入10000个随机值
for (int i = 0; i <= 10000; ++i)
{
int k = rand() % 1000000;
t.Insert(k);
}
// t.InOrder();
std::cout << t.IsBalance() << std::endl; // 输出结果
}
最后学完这些内容,感觉脑子有些懵懵的,这就对啦!仅仅只看文章是不够的,当然也不需要花费大量时间去疯狂练习,刻意培养肌肉记忆。
大家学完后,给自己一组数据,模拟AVL树的插入过程,自己画图,从无到有构建一颗完整的AVL树,你就对AVL树有一个较为深刻的认识,掌握思想才是最重要的。
代码的实现大家闲了可以去敲一下,但是建议大家在这人心浮躁的环境下可以静下心来,将自己使用的编程语言掌握熟练,跟着自己的思路去实现AVL树,即便有些出入,也可以通过参考这些完整的代码进行修改和总结,而不是使用着生疏的语法知识对照着现成的代码进行抄写。
最后,祝大家学业有成,事事顺利,看到这里还不心动点个赞吗,老铁~