RSA-CRT
前言
使用中国剩余定理对RSA进行解密,可以提高RSA算法解密的速度。
有关数论的一些基础知识可以参考以下文章: 密码学基础知识-数论(从入门到放弃)
一、中国剩余定理(CRT)
设p和q是不同的质数,且n = p*q。对于任意(X1, x2),其中 0 ≤ x1 < p 和 0 ≤ x2 < q,存在数x,其中 0 ≤ x < n。
中国剩余定理给出了以下的一元线性同余方程组:
x1 = x mod p
x2 = x mod q
因此,任何整数x (0 < x< n)都可以在其CRT表示(X1, X2)中唯一表示。
二、欧拉定理
欧拉定理是费马小定理的推广。或称为欧拉-费马定理。
n是一个正整数,a是gcd(a, n) = 1的任意整数,则a^Φ(n) = 1 (mod n)。
Φ(n)是欧拉函数,即不超过n,与n互素的正整数的个数。对于质数p, Φ § = p-1。
三、RSA正常解密流程
RSA算法流程可以参考以下文章: 公钥加密算法-RSA
m = c^d mod n(d是私钥)
为了保证安全性,要求算法中的p和q为512 bit以上长度的素数。在使用RSA算法对密文进行解密时,私钥指数d和模数n的位数一般比较大,计算起来比较困难。
可以使用中国剩余定理和欧拉函数对其进行解密。
根据中国剩余定理可以将 m = c^d mod n写成
m1=c^d mod p
m2=c^d mod q
这个时候n的位数降低了。但是d的位数依旧很大。
为了计算c^d mod p,我们可以使用欧拉定理来降低d的位数
c ^ d mod p = c ^ ( d mod Φ ( p ) ) mod p = c ^ ( d mod (p-1) ) mod p
上面式子证明如下:
d = kφ( p ) + d mod φ( p )(或者d = k(p-1) + d mod ( p-1 ))其中k是一个整数。
c ^ d = c ^( k φ ( p ) + d mod φ( p ) ) = (c ^ φ( p )) ^k * c ^ d mod φ( p )
根据欧拉定理可以得到c ^ φ ( p ) = 1 (mod p)
则c ^ d = 1^k * c ^ d mod φ( p ) = c ^ d mod φ( p ) ( mod p)
同理可得:
c ^ d mod q = c ^ ( d mod Φ ( q ) ) mod q = c ^ ( d mod (q-1) ) mod q
令dP = d mod (p-1) = e^(-1)mod(p-1)
dQ = d mod (q-1) = e^(-1)mod(p-1)
m1 = c^dP mod p
m2 = c^dQ mod q
则RSA的求解过程如下所示:
qInv = q ^ (-1) mod p
h = qInv * ( m1-m2 ) mod p
m = m2 + h*q (m为明文)
最后的求解过程可以写成:
S=CRT(m1,m2)=m2+((m1–m2)(q^(–1)modp) modp)⋅q
上面写的有些乱,可以看下面的图片:

四、举例如下:
使用中国剩余定理对以下例子进行解密
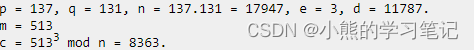
计算过程如下:

参考文章如下: Using the CRT with RSA