一、基本概念
梯度下降法又被称为最速下降法,其理论基础是梯度的概念。梯度与方向导数的关系为:梯度的方向与取得最大方向导数值的方向一致,而梯度的模就是函数在该点的方向导数的最大值。对于一个无约束的优化问题,例如
简单理解即为,随机选择一个 x 点,如同下山一样如何快速的走出一条到达山脚的路线,即利用每走一步的函数倒数及梯度的指向来进行迭代下降;同时每个人下山个性也有不同,有的激进,有的保守,这就涉及到梯度下降中的学习率设定问题(可借助之后代码演示体验);在确定下山性格后,还要设定一个到达山脚的评判标准及迭代次数判断和设定误差区间判定。
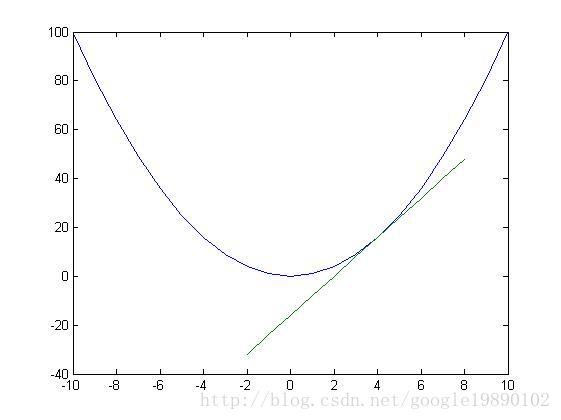
在处的切线。显然在
处函数取得最小值。沿着梯度的方向是下降速度最快的方向。具体的过程为:初始时,任取
的值,如取
,则对应的
。利用梯度下降法
,其中
为学习率,可以取固定常数。如取
,则
,对应的
,类似的
,对应的
。算法终止的判断准则是:
,其中
是一个指定的阈值。梯度的更新公式为:
二、算法流程
梯度下降算法流程(以阈值判断为例):
1、初始化:随机选取任意数
2、迭代操作:
计算梯度;
修改新的变量;
判断是否达到终止:前后两次的函数值差的绝对值小于阈值,跳出循环;
3、输出最终结果
下面以为例
import matplotlib.pyplot as plt
import numpy as np
# 定义目标函数
def f(x):
# return x ** 2 - 2 * x
return x ** 2
# 定义目标函数的导数
def df(x):
# return 2 * x - 2
return 2 * x
# 定义学习率
alpha = 0.1
# 定义初始点
x_init = 5
# 定义迭代终止的阈值
threshold = 1e-3
# 定义存储点的数组
x_list = [x_init]
y_list = [f(x_init)]
# 定义迭代次数
iteration = 0
# 进行梯度下降迭代
while True:
# 计算梯度
grad = df(x_init)
# 计算更新后的点
x_new = x_init - alpha * grad
# 将更新后的点加入列表
x_list.append(x_new)
y_list.append(f(x_new))
# 计算当前点与上一个点的差值
diff = abs(x_new - x_init)
# 输出每次迭代的结果
print(f"Iteration {iteration}: x = {x_new:.4f}, y = {f(x_new):.4f}, diff = {diff:.4f}")
# 判断是否达到迭代终止条件
if diff < threshold:
break
# 更新迭代次数和当前点
iteration += 1
x_init = x_new
# 打印结果
print("\n迭代次数:", iteration)
print("最终结果:", x_new)
# 绘制图像
x = np.linspace(-5, 6, 160)
y = f(x)
plt.plot(x, y, label="y=x^2-2x")
plt.scatter(x_list, y_list, color="red", label="iteration points")
plt.plot(x_list, y_list, linestyle="dashed", color="red")
plt.legend()
plt.show()


初始点均为5
学习率为0.1时下山的人很谨慎所以紧贴曲线,进行了30次迭代到达山脚;
学习率为0.5时下山的人很激进所以大胆跨步,只进行了1次迭代到达山脚;
若学习率跟大呢?当为0.6时候:
用同样代码对为例,设定学习率为0.8;因跨步太大和梯度符号的正负,下山路线的迭代会体现出左右横条的现象。

最后,同样是因为下山的性格选择和胆量,也会使得梯度下降区分为随机GD、批量GD、小批量GD。
三、内容补充
1、梯度消失和梯度爆炸
梯度消失:
假设在反向传播过程中,权重w<1
假如激活函数的导数也小于1,随着神经网络层数的增加,梯度会朝着指数衰减方式减小
例:
sigmoid函数 当x趋向于±∞,都会趋于平缓,导致梯度消失,这将导致损失无法再收敛,使得权重和偏差参数无法被更新,神经元失去作用,对整体的神经网络无法再起到优化调整作用。
当x趋向于±∞,都会趋于平缓,导致梯度消失,这将导致损失无法再收敛,使得权重和偏差参数无法被更新,神经元失去作用,对整体的神经网络无法再起到优化调整作用。
梯度爆炸:
假设在反向传播过程中,权重w>1且w为一个较大的值时,随着神经网络层数的增加,梯度会朝着指数爆炸的方式增加,造成的影响也是导致无法收敛,权重调整更新缓慢,计算压力过大,神经元起不到优化/调整神经网络的作用。
解决方案:
(1)更换tanh,sigmoid激活函数,转为使用Relu、LeakyRelu、Elu等激活函数
(2)使用ResNet残差结构
(3)LSTM结构
(4)做梯度截断
(5)预训练+微调
(6)权重正则化
2、多变量函数的梯度下降
可以看到,梯度就是分别对每个变量进行微分,然后用逗号分割开,梯度是用<>包括起来,说明梯度其实一个向量。
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
- 在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
假设有一个二元目标函数
![]()
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0,0)点。
我们假设初始的起点为:

初始的学习率为:
函数的梯度为:

多元函数的迭代过程:


相关学习链接:
https://blog.csdn.net/whiteBearClimb/article/details/123638005