系列文章目录
本系列开始于2022.12.25,开始记录三维重建项目课题研究时的学习笔记,其中主要分为以下几部分组成:
二、相机标定:张正友标定法
三、特征检测与匹配
四、运动恢复结构法
文章目录
目录
前言
上文介绍了相机成像原理和各个坐标系之间的转换关系,并建立了三维到二维的理想化模型,表示出了相机的内、外参数矩阵。并且对于现实情况,介绍了相机透镜可能会存在畸变相机的畸变参数。本文主要就是解决相机标定的问题,用到的方法为:张友正标定法。
一、 标定目的
进行相机标定的目的有两个:1、建立相机成像模型;2、矫正相机畸变。
1、建立相机成像模型:在上文中我们已经介绍了理想化模型的建立过程,建立的模型使空间三维点变为图像中的二维点,理论上而言如果我们知道了相机的内参矩阵和外参矩阵,能帮助我们来实现模型的逆转,以达到从图像的二维信息恢复三维信息的目的,此目的就是要通过相机标定求取未知的相机内外参数矩阵。
2、矫正相机畸变:对于上面的理想的相机模型,是小孔成像模型,但小孔成像模型有很多局限比如穿过小孔的光线少使得亮度较低。之后人们发明了透镜,但由于透镜的制造工艺,和其薄厚特性,会产生透镜畸变。透镜的畸变可以使用透镜畸变参数进行矫正,即上文提及的和
。这些畸变参数也是我们代求的内容。
二、 张正友标定法简介
下面是文章原文与翻译文献。
原文:Flexible camera calibration by viewing a plane from unknown orientations
张氏标定法使用二维方格组成的标定板进行标定,采集标定板不同位姿图片,提取图片中角点像素坐标,通过单应矩阵计算出相机的内外参数初始值,利用非线性最小二乘法估计畸变系数,最后使用极大似然估计法优化参数。该方法操作简单,而且精度较高,可以满足大部分场合。
准备工作如下:
- 定焦相机:如果你的相机是变焦的,那么在获取图像序列时不要使用其变焦功能,比如你的手机想进行相机标定,那么在拍照时就不能点击屏幕让其进行变焦,本次使用无人机焦距可以手动控制,所以在进行标定时使用的焦距和后期进行三维重建时使用的焦距要保持一致。如果焦距发生变换,标定出相机的内参矩阵也会发生变换
- 分辨率一般已知。
有的博文说需要分辨率,但是目前还没发现用在哪。
- 棋盘格:使用棋盘格的目的是其简单容易准备,并且可以很迅速的通过角点检测算法检测角点。我们可以多次改变棋盘的方位来获取图像,以求获得更丰富的坐标信息。

多个角度拍摄图例子如下:

三、标定原理
3.1 输入输出
- 输入:使用定焦相机拍摄的棋盘格的图像序列。
- 输出:相机内外参数矩阵、畸变参数等。
为后面三维重建程序所用的主要是内参矩阵和畸变参数,其他后期在进行讨论。
内参矩阵K:
上文中给出的外参矩阵为: 是一个3×4的矩阵,但是最后一列为0,并且所求参数都位于前三列,所以为了计算和表达的方便,将内参矩阵写为如下形式:
是一个3×4的矩阵,但是最后一列为0,并且所求参数都位于前三列,所以为了计算和表达的方便,将内参矩阵写为如下形式:

则:

表示为一个矩阵被为3×3矩阵和一列0向量。下面讨论的内参矩阵即为3×3的K。
为5个相机内参。
这里原文对于内参矩阵表示为A,本文表示为K,勿混淆。
外参矩阵:

此矩阵为4×4的矩阵,可以将旋转矩阵R的列向量分别命名为,写成以下形式:
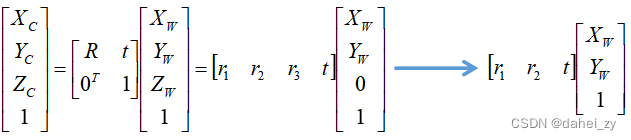
此处,为相机坐标,
为世界坐标,R为旋转矩阵,t为平移向量。
为什么箭头左边Zw=0,并且箭头右边
消失?
假定在世界坐标系中,坐标原点选择在棋盘的左上角特征点,棋盘的平面刚好是与Xw-Yw平面重合,Zw轴穿越平面垂直向上,这时棋盘所有特征点的Zw=0,特别方便后面的计算。可直接转换成上式的形式,即省略了对Zw轴的旋转量
。
在阅读其他大佬博文时,包括张氏标定法原文中,箭头位置为等号,可是因为维度并不相等,所以在此处感觉箭头会更准确一点。
畸变参数:
上文介绍的和
5个畸变参数,但是张正友标定法,不求切向畸变。所以只有
3个参数。
所以最后的数学模型可以简化为下式:

为像素坐标,
为尺度因子,
为5个相机内参,R为旋转矩阵,t为平移向量,为相机外参,
为世界坐标。
之前的公式对比和符号详情可参考上一文章。
3.2 单应性矩阵
3.2.1 单应性变换
单应性变换是齐次坐标之间的线性变换,在三维重建中其主要描述了物体在世界坐标和像素坐标之间的变换,对应的变换矩阵为单应性矩阵H。综上,在此H如下:

单应性主要应用在图像矫正、图像拼接、相机位姿估计、SLAM等方面。
3.2.2 求解单应性矩阵(“4点法”)
现在我们已经有一个能将一个坐标为另一个坐标
的单应性矩阵H了,那么问题来了:怎么进行求解呢?

两个坐标之间的表达关系:

根据矩阵论,为了解出单应性矩阵中的所有元素,需要知道H有几个自由度,以便找到相应数目的对应点,解出H。
自由度:式中的参数为n,在这个式子的约束下,能够进行自由变换的变量的数目(最多)为该约束下的自由度。
在此因为H有9个参数,所以很多人认为其有9个自由度,其实不然,在此,我们使用的是齐次坐标,可以进行任意尺度的缩放,换一种方法说明就是,在上式箭头的右边,我们对分子分母同时乘一相同的数,等式不变。所以H和kH是等价的(k为一不为零参数),所以:
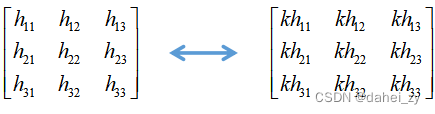
此时,将k设为:,则
,所以H等价于:

所以H的在此约束下能自由变化的参数减少了一个,所以H 的自由度其实为8。当其自由度为8时,有以下两种处理方式:
1、令;
2、添加约束条件:令其模为1
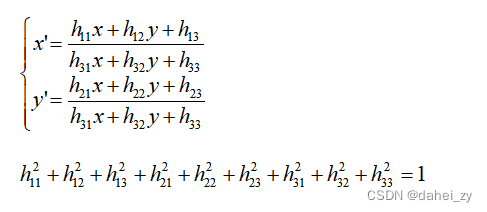
以第二种方法为例,将等式展开整理:
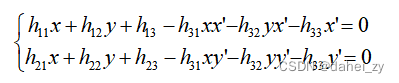
假设已知对应点数为n所以可以得到如下方程:

理论上,由于其自由度为8,并且一组对应点可以建立一组(两个,第一行和第二行)方程,所以我们需要8个方程即,4组点来计算H。
但是在真实的应用场景中,我们计算的点对中都会包含噪声。比如点的位置偏差几个像素,甚至出现特征点对误匹配的现象,如果只使用4个点对来计算单应矩阵,那会出现很大的误差。因此,为了使得计算更精确,一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解,所以实际使用中一般会用其他优化方法,如奇异值分解、Levenberg-Marquarat(LM)算法等进行求解。
3.2.3 从棋盘格到单应性矩阵
总体过程:
1、打印一张棋盘格标定图纸,将其贴在平面物体的表面。
2、拍摄一组不同方向棋盘格的图片,可以通过移动相机来实现,也可以移动标定图片来实现。
3、对于每张拍摄的棋盘图片,检测图片中所有棋盘格的特征点(角点,也就是下图中黑白棋盘交叉点)。我们定义打印的棋盘图纸位于世界坐标系Zw=0的平面上,世界坐标系的原点位于棋盘图纸的固定一角。像素坐标系原点位于图片左上角。
4、因为棋盘标定图纸中所有角点的空间坐标是已知的,这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的,如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒),就可以根据LM等优化方法得到其单应矩阵H。当然计算单应矩阵一般不需要自己写函数实现,MATLAB和OpenCV中就有现成的函数可以调用。
四、数学推导
首先,我们已经知道了相机成像模型中的单应性矩阵的形式,并且,在上文可以用4点法求解H,但是在这中间,内外参数矩阵是混在一起的,因为每张图片的内参矩阵的都是固定的,所以,我们在那进行内参矩阵的求解,再进行外参矩阵求解。

其中s为非零常数 ,在上一节中可以知道,因为H这里使用的是齐次坐标系,也就是说可以进行任意尺度的缩放,s可以简单理解为缩放的倍数。
在求解时主要用的是旋转矩阵的性质,为啥说是内参求解用的时外参的性质,这个下面在进行求解时会介绍,在此先介绍旋转矩阵的一些性质。
4.1 旋转矩阵的性质
首先我们知道,在外参矩阵中的旋转矩阵R,可以写成,
分别为世界坐标系绕X,Y,Z轴旋转产生的旋转坐标(在上文以详细说明)。我们对其进行分开讨论。对于
,

为正交矩阵,根据正交矩阵的性质:
,我们不难证明,并且
同为正交矩阵。
从正交矩阵的一些性质中我们不难找到:
正交矩阵的行列式值必定为+1或-1。
并且行列式值为+1的正交矩阵,称为特殊正交矩阵,它是一个旋转矩阵。
行列式值为-1的正交矩阵,称为瑕旋转矩阵。瑕旋转是旋转加上镜射。镜射也是一种瑕旋转。
由此我们也可以得出旋转矩阵是正交矩阵。并且所有特殊正交矩阵形成一个子群,称为特殊正交群。所以,旋转矩阵与旋转矩阵的乘积也是一个旋转矩阵,即R也为正交矩阵。
所以对于旋转矩阵R,其具有正交矩阵的性质但是,我们主要用到的性质有以下两点:
- R所有列向量单位向量,且互相正交。
- R的逆等于它的转置。
4.2 内参求解
通过上一节,我们知道了R的列向量相互正交且为单位向量,所以,在此,满足以上性质。为利用此关系,将H转化为列向量形式得到如下关系:
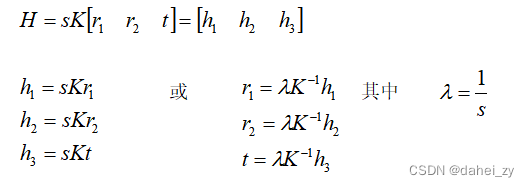
接下来运用性质:1、相互正交;2、
为单位向量,模长相等并为1。得到如下公式:

令:

不难看出B沿对角线对称。

以上公式可以写成如下形式: ,
,为H的第i列列向量,则令:

带入整理得:

原文中没有
,但是为了后期计算的严谨性在此加上
。虽然加上此参数,但是因为其为缩放因子,并且在等式中可以约去,所以不影响其他公式。
令:

则化简如下:

即:
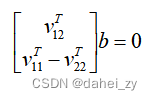
根据n张不同角度的标定图片,最终我们得到了一个矩阵集合 Vb=0 ,其中V是一个 (2n x 6) 的矩阵。
一张图片可以得到一组(2个)上述的等式。拍摄了n张不同角度的标定图片,我们可以得到2n个等式。其中,通过前面已经计算好的单应矩阵得到,因此是已知的,而b中6个元素是待求的未知数。因此,至少需要保证图片数 n>=3,我们才能解出b。但是此时带有一缩放因子
。b已知则B已知。
这里得n是图片得个数,而上面进行单应性矩阵求解的n是两张图片中对应点的个数。
再根据如下公式求取内参矩阵:
4.3 外参求解
现在H已知,K也已知,可以进行外参的求解了,但是我们在此前进行运算是一直没用到,但遵循坐标轴之间彼此正交可以得到
,则:

并且根据,则
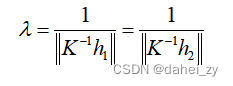
确实不知道为啥又求了一遍。 实际情况下,数据中是存在噪音的,所以计算得到的旋转矩阵R并不一定能满足旋转矩阵的性质。所以通常根据奇异值分解来得到旋转矩阵R。
五、最大似然优化
上述为理论推导,但是在实际应用过程中往往使用最大似然估计法进行优化。(最小化x, x’的位置来求解)。
- 标定棋盘格图片n张
- 棋盘格图片有m个角点
- 空间点坐标X
- 空间点在图像对应的像素坐标x
- 空间点经过相机内参K,外参R,t变换后得到坐标x'
- 考虑畸变时要加上畸变参数(在这里只考虑
,其他参数影响不大,增加反而会使模型负责且不稳定)
- 假设:噪声独立同分布

求最小是非线性优化问题可以通过LM(Levenberg-Marquardt)算法解决。一般将k1,k2初值设为0。
总结
介绍了张正友标定法的原理及求解过程,可以由棋盘格图像序列求解相机内外参数矩阵,用于后续重建工作。
代码如下:
daheizy/Camera-Calibration: 张正友相机标定,使用棋盘格输入序列进行相机标定,输出相机内参;畸变参数;相机内参等。 (github.com)
参考
2、张正友标定法翻译