深度学习|3|多层感知机正确打开方式

单层感知机

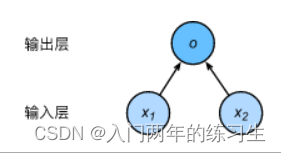
感知机与线性回归的本质区别：输出不同

• 线性回归输出的是一个连续的实值

• 感知机输出的是一个离散的类{0， 1}或{-1, 1}

因此，感知机可视为一个用于二分类的分类器：当输出为0时，表明为第一类，输出为1时，表明为第二类。

感知机的训练方法

1. 初始化w和b
2. 循环：
3.    ~~   如果 $y_i\times (<w_i,x_i>+b)\le 0$, 则:
4.      ~~~~      令$w\leftarrow w+y_i{x}_i,b\leftarrow b+y_i$
5. 直到全部类别正确分类

上述过程中，损失函数可写为：

$l=\text{max}(0,-y<w,x>)$

人工智能第一次危机：XOR问题

感知机无法解决XOR问题：很难用一个线性函数来划分XOR的问题。

此时，多层感知机出场来解决问题。

多层感知机

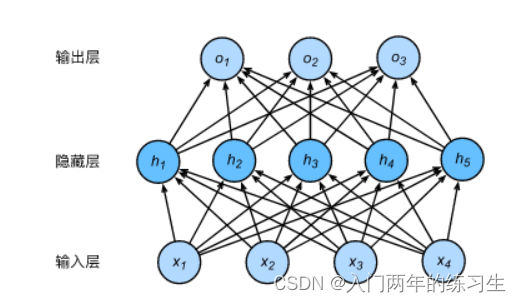
多层感知机提出的目的之一，是为了让其解决XOR问题。

对于若干个特征，首先对部分特征进行分类，并对另一部分特征进行分类。两部分分类的结果，再进行分类，就能解决XOR问题。
直观上，多层感知机的最大特点就在于他多了一个隐藏层。

给定一个dim=m的输入，要求最终输出一个dim=n的输出向量(类别)，那么一种直觉上的实现方式就是：

$$\left[\begin{array}{c}{h}_1\\ ⋮\\ h_k\end{array}\right]=\left[\begin{array}{ccc}{w}_1{1}^{(0)}& \cdots & w_1{m}^{(0)}\\ ⋮& \ddots & ⋮\\ w_k{1}^{(0)}& \cdots & w_n{m}^{(0)}\end{array}\right]\cdot \left[\begin{array}{c}{x}_1\\ ⋮\\ x_m\end{array}\right]+\left[\begin{array}{c}{b}_1^{(0)}\\ ⋮\\ b_k^{(0)}\end{array}\right]$$

$$\left[\begin{array}{c}{o}_1\\ ⋮\\ o_n\end{array}\right]=\left[\begin{array}{ccc}{w}_1{1}^{(1)}& \cdots & w_1{k}^{(1)}\\ ⋮& \ddots & ⋮\\ w_n{1}^{(1)}& \cdots & w_n{k}^{(1)}\end{array}\right]\cdot \left[\begin{array}{c}{h}_1\\ ⋮\\ h_k\end{array}\right]+\left[\begin{array}{c}{b}_1^{(1)}\\ ⋮\\ b_n^{(1)}\end{array}\right]$$

以上写成矩阵形式就是

$$h=W^{(0)}x+b^{(0)}$$

$$o=W^{(1)}h+b^{(1)}$$

但其实到此依旧是单层网络
上述的公式带入后，由如下形式：

$${o=W}^{(1)}(W^{(0)}{x+b}^{(0)})+b^{(1)}$$

进而，展开后可写成：

$${o=W}^{(1)}{W}^{(0)}{x+W}^{(1)}{b}^{(0)}+b^{(1)}$$

其中，$W^{(0)}\in {\mathbb{R}}^{k\times m},W^{(1)}\in {\mathbb{R}}^{k\times n},b^{(0)}\in {\mathbb{R}}^{k\times 1},b^{(1)}\in {\mathbb{R}}^{n\times 1}$

那么，$W=W^{(1)}\times W^{(0)}\in {\mathbb{R}}^{n\times m},b=W^{(1)}{b}^{(0)}+b^{(1)}\in {\mathbb{R}}^{n\times 1}$

本质上，公式可写成

$$o=Wx+b$$

因此，本质上依然是单层神经网络。

造成上述问题的最大原因在于：神经元在传递过程中缺少非线性性。

一个输入，乘以若干个矩阵，本质上等价于乘以一个矩阵。

因为矩阵的乘法，是一个线性的过程：变换过去以后，可以变换回来。

线性变换的基本形式：

$$y=Wx$$

改变这种情况的方法就是，为模型加入非线性变换。

加入非线性变换，激活函数

Sigmod函数

$$\text{x}=\frac{1}{1+\text{exp}(-x)}$$
画出图像

import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

import torch
import matplotlib.pyplot as plt

plt.figure(figsize=(2, 2))

x = torch.arange(-5, 5, 0.1, requires_grad=True)
y = x.sigmoid()
plt.scatter(x.detach().numpy(), y.detach().numpy())
plt.show()

在什么情况下适合使用 Sigmoid 激活函数呢？

Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1，因此它对每个神经元的输出进行了归一化；
用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适；
梯度平滑，避免「跳跃」的输出值；
函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率；
明确的预测，即非常接近 1 或 0。

Sigmoid 激活函数存在的不足：

梯度消失：注意：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播。
不以零为中心：Sigmoid 输出不以零为中心的,，输出恒大于0，非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。
计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂，计算机运行起来速度较慢。

y.sum().backward()
plt.figure(figsize=(3, 3))
plt.scatter(x.detach().numpy(), x.grad.detach().numpy())
plt.show()

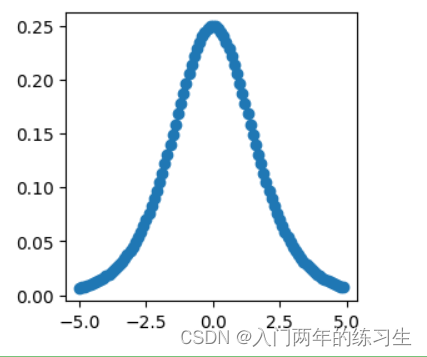
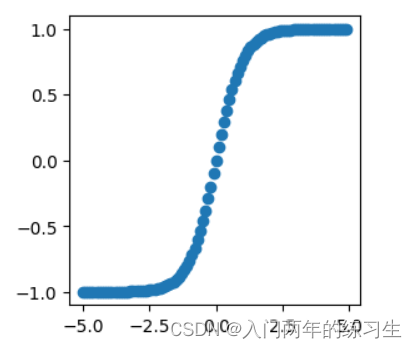
Tanh函数

$$\text{x}=\frac{1-\text{exp}(-2x)}{1+\text{exp}(-2x)}$$

y = x.tanh()
plt.figure(figsize=(3, 3))
plt.scatter(x.detach().numpy(), y.detach().numpy())
plt.show()

tanh存在的不足：

与sigmoid类似，Tanh 函数也会有梯度消失的问题，因此在饱和时（x很大或很小时）也会「杀死」梯度。
注意：在一般的二元分类问题中，tanh 函数用于隐藏层，而 sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。

x.grad.zero_()
y.sum().backward()
plt.figure(figsize=(3, 3))
plt.scatter(x.detach().numpy(), x.grad.detach().numpy())
plt.show()

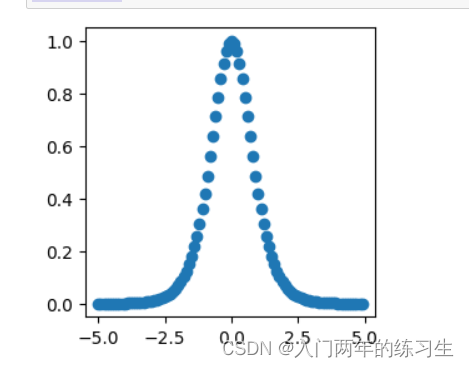
Relu函数

$$\text{relu}(x)=\{\begin{array}{ll}0,& \text{x}\le 0\\ x,& \text{x > 0}\end{array}$$

y = x.relu()
plt.figure(figsize=(3, 3))
plt.scatter(x.detach().numpy(), y.detach().numpy())
plt.show()

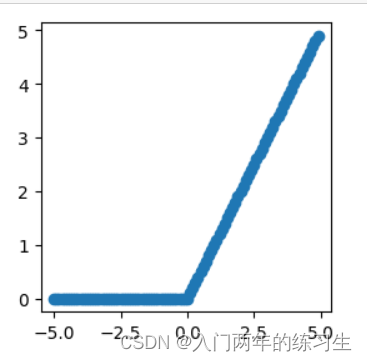
x.grad.zero_()
y.sum().backward()
plt.figure(figsize=(3, 3))
plt.scatter(x.detach().numpy(), x.grad.detach().numpy())
plt.show()

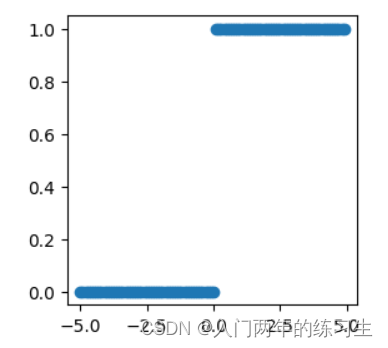
在实际中，relu函数有着更简洁的表达：

$$\text{relu}(x)=\text{max}(x,0)$$

ReLU 函数是深度学习中较为流行的一种激活函数，相比于 sigmoid 函数和 tanh 函数，它具有如下优点：

当输入为正时，导数为1，一定程度上改善了梯度消失问题，加速梯度下降的收敛速度；
计算速度快得多。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。
被认为具有生物学合理性（Biological Plausibility）,比如单侧抑制、宽兴奋边界（即兴奋程度可以非常高）

ReLU函数的不足：

Dead ReLU 问题。当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零；
【Dead ReLU问题】ReLU神经元在训练时比较容易“死亡”。在训练时，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活。这种现象称为死亡ReLU问题，并且也有可能会发生在其他隐藏层。
不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心，ReLU 函数的输出为 0 或正数,给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。

对于每个神经元来说，都配置有一个激活函数。

其物理意义在于：当其阈值足够大的时候，才会激活(向下层传递)，否则不会传递。

实际上，这种物理意义有着脑神经科学的解释。

因此，多层感知机的总体形式是：

$$h=\delta (W^{(0)}{x+b}^{(0)})$$

$$o=\text{softmax}(W^{(1)}{h+b}^{(1)})$$

总结

多层感知机是一个基于神经网络的多层的分类模型。

其输出为softmax后的输出，即输出为一个概率；

其多层来自于激活函数的非线性性。

最常用的激活函数为Relu函数，因为其计算最为方便。