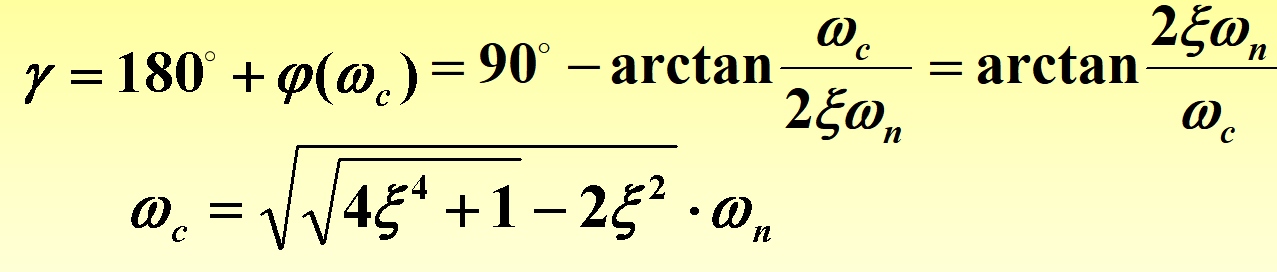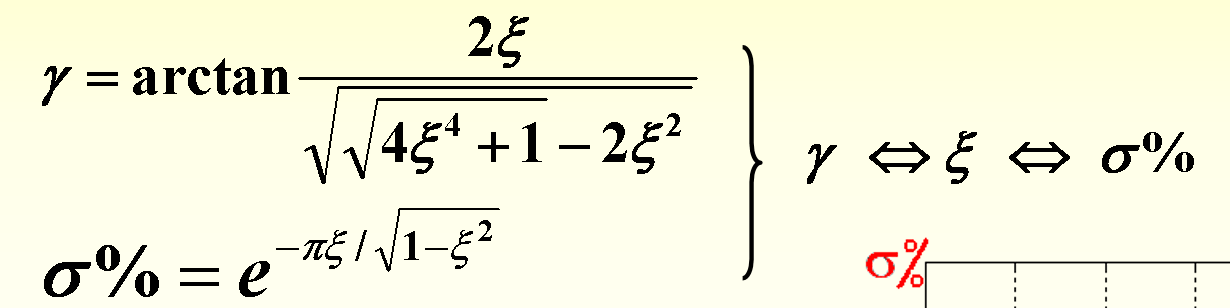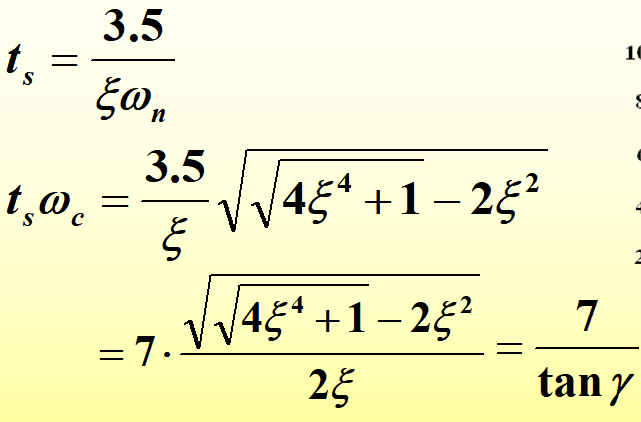todo
确定延时环节 e τ ω e^{\tau\omega} eτω的性质
指标转换
补充知识
Bode
卢姥爷对bode的运用很熟练。比如下面的*-20 -40 -60特殊解法，或者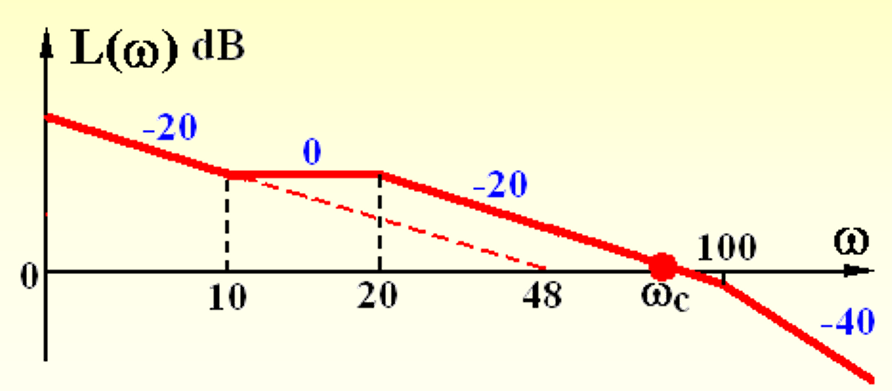
这种图分析出 ω c = 48 ∗ 2 \omega_c=48 * 2 ωc=48∗2
三频段概念及设计原则
低频与稳态误差相关，K越大，稳态误差越小；型别越高，跟踪能力越强
高频段与抗干扰能力有关，噪声通常为高频信号，对应增益越小越好
频域稳定判据
频域稳定判据的好处：
1.可以通过开环特性判断闭环
2.可以研究包含延迟的环节【HOW？】
3.可以调节参数
技巧：算角度，用表达式分子角度减去分母角度
奈奎斯特曲线绘制
-
✨当[s]平面虚轴上有开环极点时,奈氏路径要从其右边绕出半径为无穷小的圆弧
另外，[G]平面对应要补充大圆弧-90° v v v； 根据零、极点情况确定是否穿过-90 v v v°线：分析距离虚轴最近的开环零极点，若为零点，则不穿过，否之则穿过上面这种方法实际上体现了一定的几何意义，在最最开始的时候，最靠近虚轴【无论正负！】的零极点发挥的作用最大，可以只看他
-
每个零极点贡献的角度为：s从j0到j+∞，从零极点指向 j s js js的夹角。
例题【建议自己做】
例题
分析： τ \tau τ离得近，所以j0附近只分析 τ \tau τ，在分子处，相角逐渐减小，幅值逐渐变大，因此朝左上方扭。
奈奎斯特稳定判据
尾1
用开环！
积分环节注意补充虚线
临界稳定情况：奈奎斯特碾过(-1,j0)
- 使用开环函数
- 公式为 Z = P − R = P − 2 ( N + − N − ) Z=P-R=P-2(N^+-N^-) Z=P−R=P−2(N+−N−)
- Z是闭环右半平面极点【不包括纯虚轴，是待求解的值】P是开环右半平面极点【不包括纯虚轴】
- N + N^+ N+为(-1,j0)左侧正穿越，从上到下；对应相角增加的情况
在对数频域曲线中，向下穿过相角-180°代表角度减小，对应 N − N^- N−
- 怎么判断正，负通过，或者包围了多少圈，可以想象一个小人在(-1,j0)看奈奎斯特曲线从 s = 0 s=0 s=0转到 s = + ∞ s=+∞ s=+∞，看小人有没有转圈，是什么方向【逆时针为正】。
在BODE上的应用
结论：在L（ ω \omega ω）>0的情况下，看相角穿越-180°【 + 2 k π +2k\pi +2kπ】的次数。
- BODE是尾1
- 如果相角贴着负实轴（贴着180°），算半个，视情况而定是 N + N^+ N+【相角增加】还是 N − N^- N−【相角减小】。
- 注意虚线，在纯虚轴上的开环极点在bode上要跳90 v v v°
比如： 40 s [ ( s 5 ) 2 + 1 ] \frac{40}{s\left[\left(\frac{s}{5}\right)^{2}+1\right]} s[(5s)2+1]40，在 ω = 0 , ω = 5 \omega=0, \omega=5 ω=0,ω=5处都有虚线，分别对应90°、180°，参考例题：好题目呐
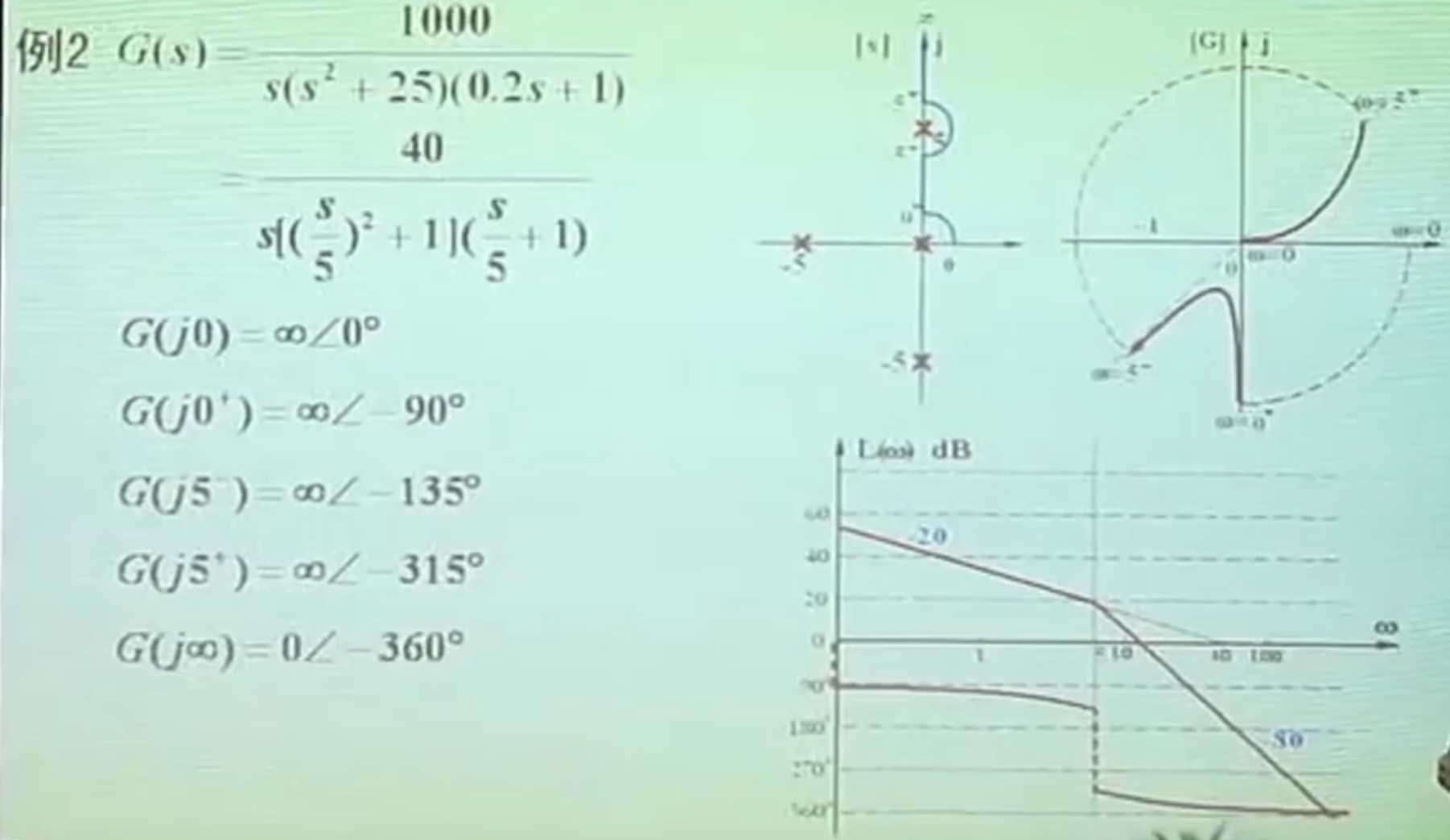
补充提问：如果K下降，在BODE上有
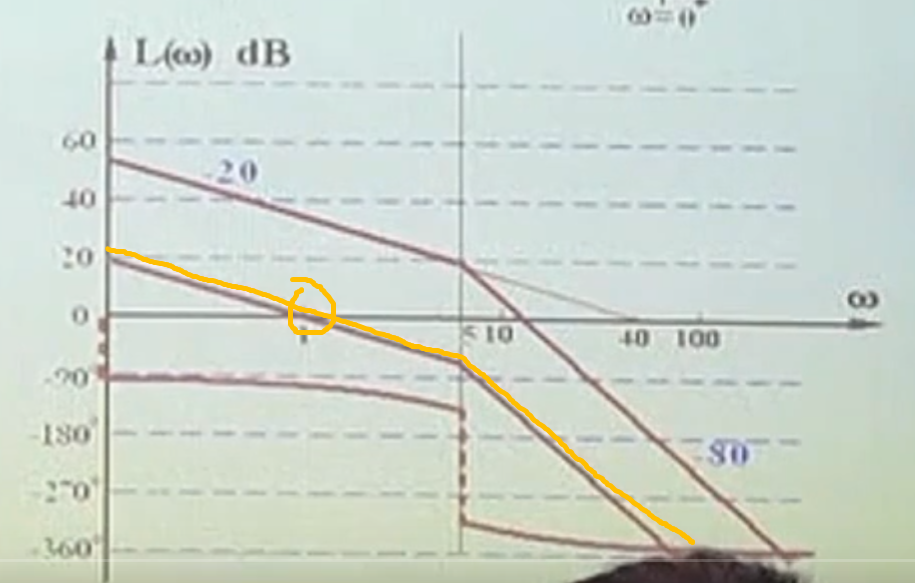
此时是不是不穿越了呢？
补充回答：不是。应该以奈奎斯特为准，BODE只是近似，实际上的BODE图为：
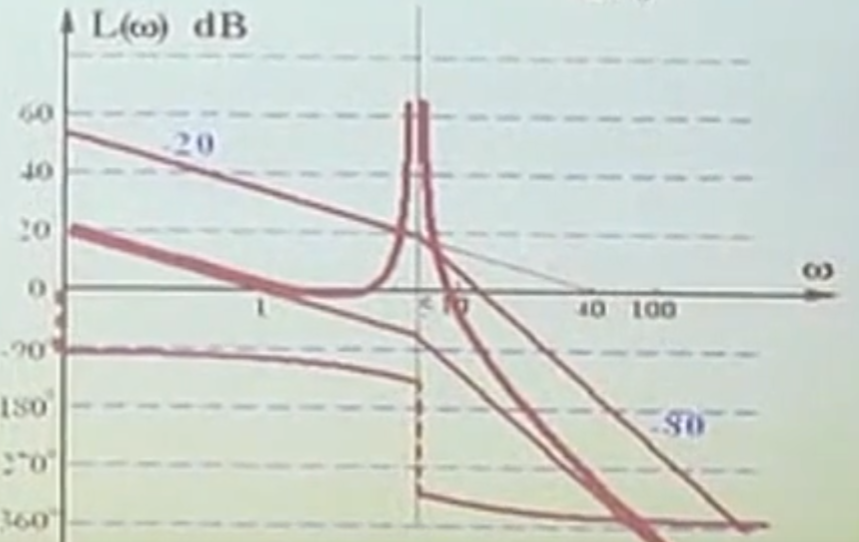
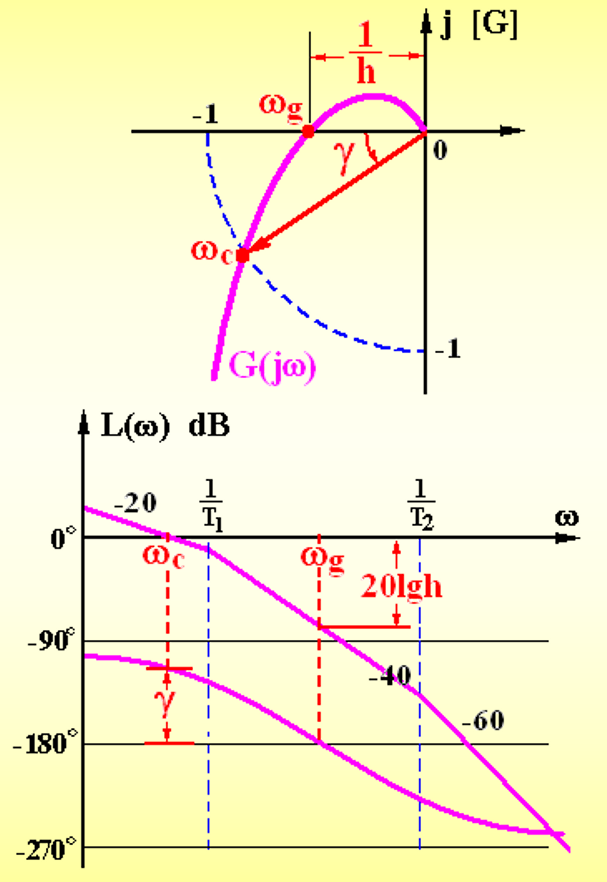
稳定裕度
之前的稳定性判据只能二元判断是否稳定，需要引入一个判断稳定程度的指标
定义
最小相位系统
所有的开环零点极点都在左边【负实轴？包括虚轴吗】
稳定裕度各个参数【在开环下计算】
注意幅值裕度有个倒数关系
闭环各个参数✨✨
（3）带宽频率通过计算得出，代入 ω = ω b \omega=\omega_b ω=ωb
- 实际工程中应用广泛
- 也可以估算系统性能
- 补充知识
Φ ( j ω ) \Phi(j \omega) Φ(jω)：闭环传函 G ( j ω ) G(j \omega) G(jω)：开环传函
Φ ( j ω ) = G ( j ω ) 1 + G ( j ω ) = M ( ω ) ⋅ e j ϕ ( ω ) \Phi(j \omega)=\frac{G(j \omega)}{1+G(j \omega)}=M(\omega) \cdot e^{j \phi(\omega)} Φ(jω)=1+G(jω)G(jω)=M(ω)⋅ejϕ(ω)
开环到闭环的直接转化*
这部分个人感觉是为了理解闭环参数的概念，不做考试要求
等M圆
【用来求闭环幅值相等各点在开环复平面的位置】
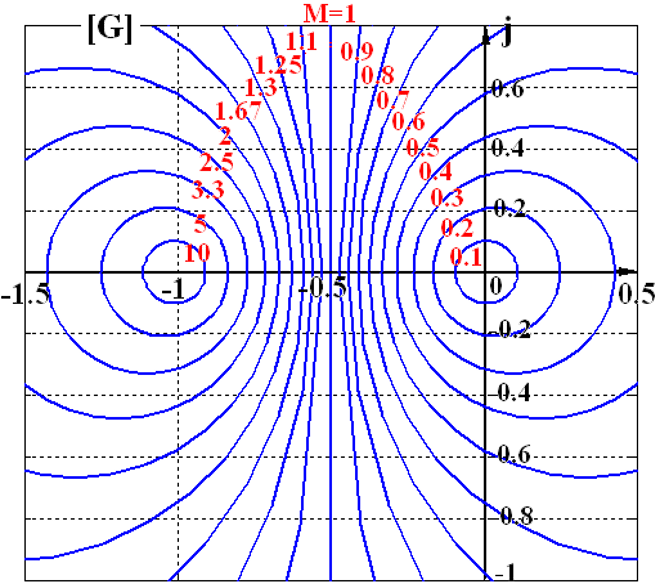
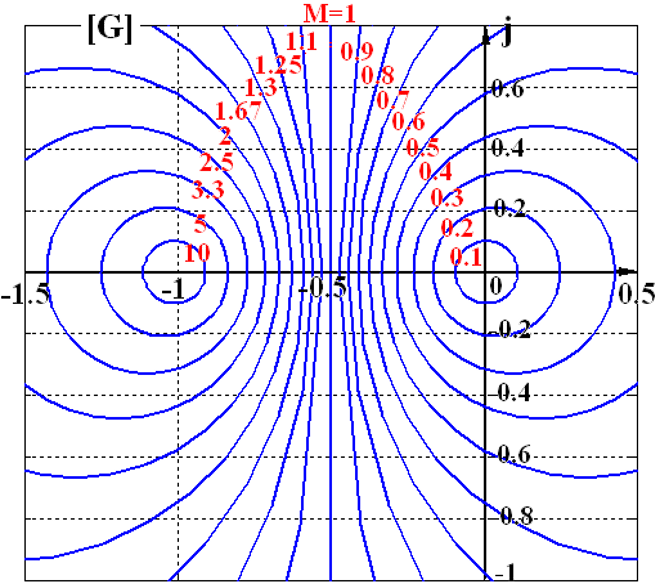
等N圆
【用来求闭环相角相等各点在开环复平面的位置】
bode图上开环幅值相角->闭环幅值相角**
这个应该不会作为考研题目出现
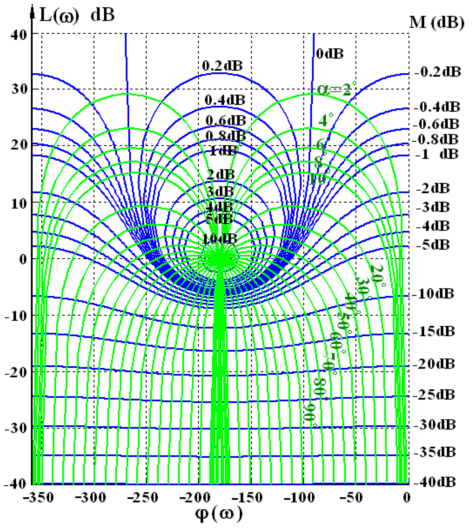
根据开环的 L ( ω ) L(\omega) L(ω)和( M ( d B ) M(dB) M(dB))确定点，找到对应的两圆即为闭环幅值、相角
稳定裕度的物理意义
相角裕度：可延迟时间
幅值裕度：可放大倍数
注意这里的延时环节，之前没怎么接触过，它只改变相角，不改变幅值；与比例环节正好相反；改变的角度是 57.3 ° τ ω 1 57.3°\tau\omega_1 57.3°τω1【有待商榷】
稳定裕度的计算
通常情况下，用粗略解就好【幅值才有粗略解，相角没有】
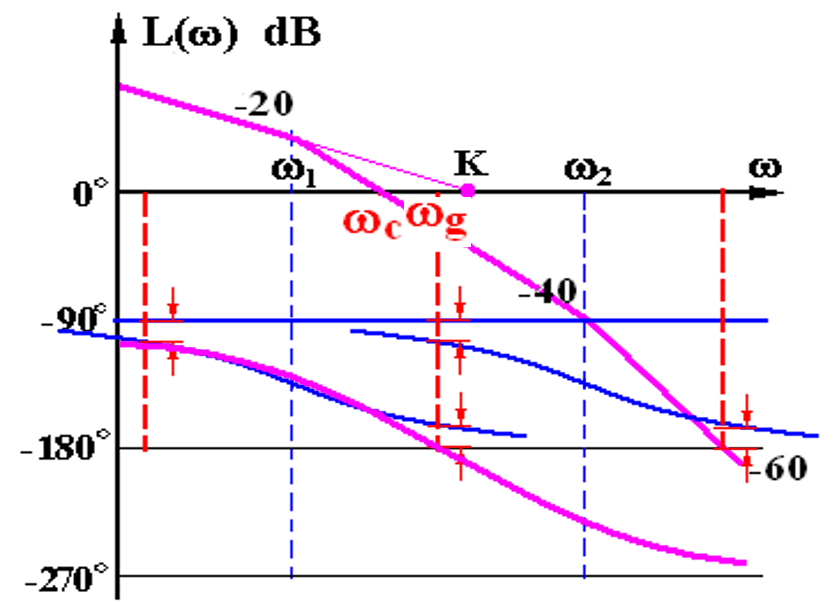
*对于-20 -40 -60的一种特殊解法
-180°一定处于 ω g = ω 1 ⋅ ω 2 \omega_g=\sqrt{\omega_1 \cdot \omega_2} ωg=ω1⋅ω2处，即两个转折点处【数学关系】
【同时，截止频率 ω c = ω 1 ⋅ k \omega_c=\sqrt{\omega_1 \cdot k} ωc=ω1⋅k】
系统时域性能与开环、闭环各参数转化关系✨✨
概述
传递函数
开环参数常用指标为： ω c \omega_c ωc， γ \gamma γ
系统时域性质常用指标为： t s t_s ts， δ % \delta\% δ%， ξ \xi ξ， ω n \omega_n ωn
闭环性能常用指标为： M r M_r Mr， ω b \omega_b ωb
系统性能【主要是为了帮助理解】
方法一：开环的时域分析（二阶系统）【复杂不常用但是基础】
经过计算，相角裕度 γ \gamma γ和超调量 δ \delta δ都是关于阻尼比 ξ \xi ξ的函数；三者已知任意一个可以知道其他两个
同时剪切频率 ω c \omega_c ωc与阻尼比 ξ \xi ξ和 ω n \omega_n ωn均有关：
ω c = 4 ξ 4 + 1 − 2 ξ 2 ⋅ ω n \omega_{c}=\sqrt{\sqrt{4 \xi^{4}+1}-2 \xi^{2}} \cdot \omega_{n} ωc=4ξ4+1−2ξ2⋅ωn
同时，若把剪切频率 ω c \omega_c ωc看作已知，由公式 t s = 3.5 ξ ω n t_s=\frac{3.5}{\xi\omega_n} ts=ξωn3.5，可以得到 t s ⋅ ω c t_s \cdot \omega_c ts⋅ωc的表达式，进而得到调节时间 t s t_s ts与相角裕度 γ \gamma γ(阻尼比 ξ \xi ξ)关系
三者关系如图：
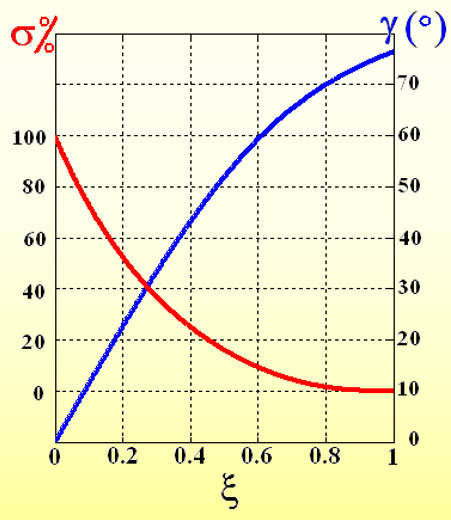
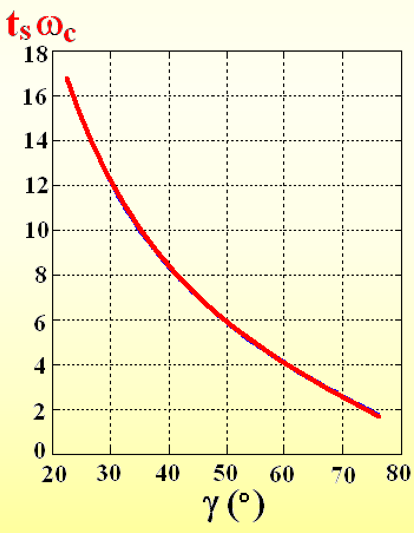
不那么重要的计算过程
调节时间 t s t_s ts与阻尼比 ξ \xi ξ的函数
方法二：开环的频域分析（高阶）【经验公式，常用✨】
可以正着用，也可以倒着用。通常的适用范围是 ( 3 5 ∘ ≤ γ ≤ 90 ∘ ) \left(35^{\circ} \leq \gamma \leq \mathbf{9 0}^{\circ}\right) (35∘≤γ≤90∘)
从性质上：
- 超调量 δ \delta δ只与相角裕度 γ \gamma γ有关
- 调节时间 t s t_s ts与剪切频率 ω c \omega_c ωc和相角裕度 γ \gamma γ都有关
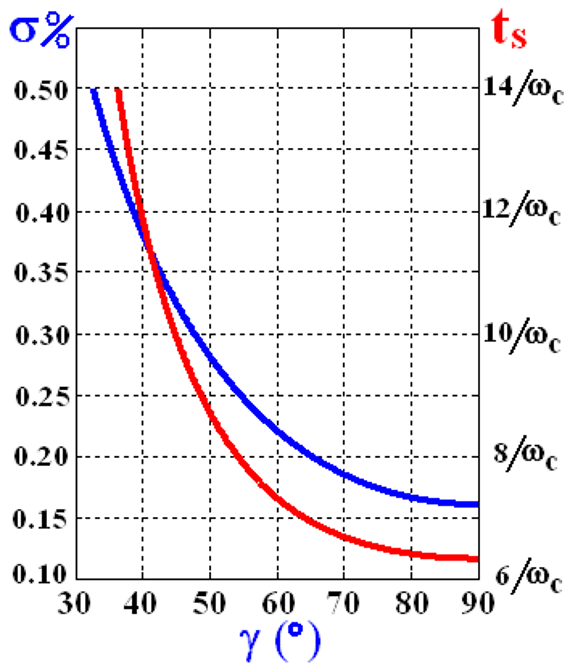
方法一：闭环的时域分析（二阶）
经过计算，谐振峰值 M r M_r Mr、相角裕度 γ \gamma γ和超调量 δ \delta δ都是关于阻尼比 ξ \xi ξ的单调函数；四者已知任意一个可以知道其他三个
同时带宽频率 ω b \omega_b ωb与阻尼比 ξ \xi ξ和 ω n \omega_n ωn均有关：
ω b = ω n 1 − 2 ξ 2 + 2 − 4 ξ 2 + 4 ξ 4 \begin{array}{l} \omega_{b}=\omega_{n} \sqrt{1-2 \xi^{2}+\sqrt{2-4 \xi^{2}+4 \xi^{4}}} \end{array} ωb=ωn1−2ξ2+2−4ξ2+4ξ4
同时，若把带宽频率 ω b \omega_b ωb看作已知，由公式 t s = 3.5 ξ ω n t_s=\frac{3.5}{\xi\omega_n} ts=ξωn3.5，可以得到 t s ⋅ ω b t_s \cdot \omega_b ts⋅ωb的表达式，进而得到调节时间 t s t_s ts t s t_s ts与谐振峰值 M r M_r Mr(阻尼比 ξ \xi ξ)关系
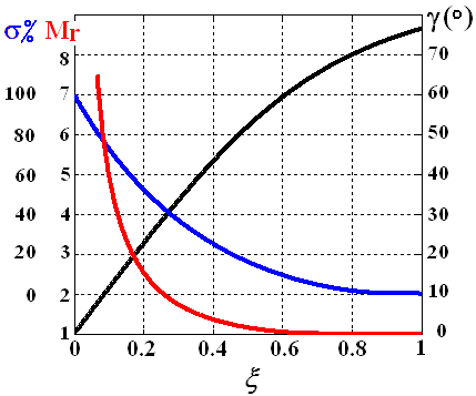
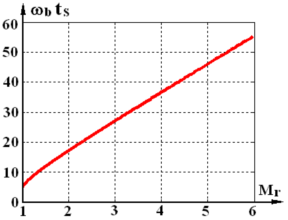
方法二：闭环的频域分析（高阶）
σ % = [ 0.16 + 0.4 ( M r − 1 ) ] × 100 % t s = π ω c [ 2 + 1.5 ( M r − 1 ) + 2.5 ( M r − 1 ) 2 ] M r ≈ 1 sin γ ( 3 5 ∘ ≤ γ ≤ 9 0 ∘ ) \begin{array}{c} \sigma \%=\left[0.16+0.4\left(M_{r}-1\right)\right] \times 100 \% \\\\ t_{s}=\frac{\pi}{\omega_{c}}\left[2+1.5\left(M_{r}-1\right)+2.5\left(M_{r}-1\right)^{2}\right] \\\\ M_{r} \approx\frac{1}{\sin \gamma} \quad\left(35^{\circ} \leq \gamma \leq 90^{\circ}\right) \end{array} σ%=[0.16+0.4(Mr−1)]×100%ts=ωcπ[2+1.5(Mr−1)+2.5(Mr−1)2]Mr≈sinγ1(35∘≤γ≤90∘)
与开环几乎一致【注意有一个开环参数剪切频率 ω c \omega_c ωc】
事实上闭环截止频率 ω b \omega_b ωb和 ω c \omega_c ωc往往是一个数量级，可以替换
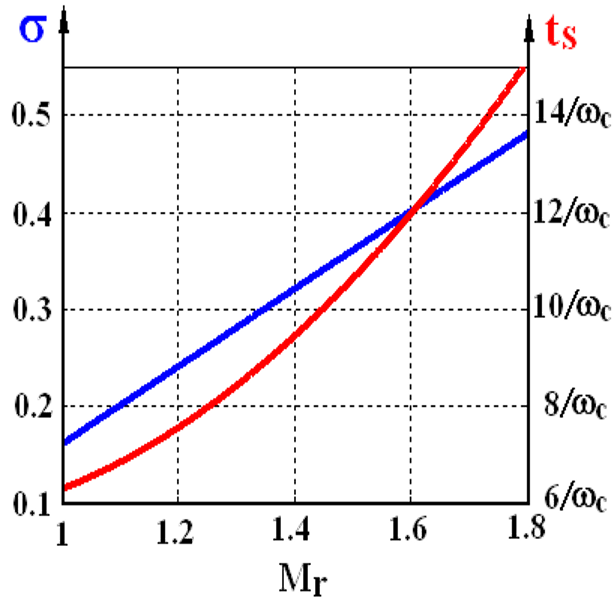
总结【复习时只用看总结】
三个公式
σ % = [ 0.16 + 0.4 ( M r − 1 ) ] × 100 % t s = π ω c [ 2 + 1.5 ( M r − 1 ) + 2.5 ( M r − 1 ) 2 ] M r ≈ 1 sin γ ( 3 5 ∘ ≤ γ ≤ 9 0 ∘ ) \begin{array}{c} \sigma \%=\left[0.16+0.4\left(M_{r}-1\right)\right] \times 100 \% \\\\ t_{s}=\frac{\pi}{\omega_{c}}\left[2+1.5\left(M_{r}-1\right)+2.5\left(M_{r}-1\right)^{2}\right] \\\\ M_{r} \approx\frac{1}{\sin \gamma} \quad\left(35^{\circ} \leq \gamma \leq 90^{\circ}\right) \end{array} σ%=[0.16+0.4(Mr−1)]×100%ts=ωcπ[2+1.5(Mr−1)+2.5(Mr−1)2]Mr≈sinγ1(35∘≤γ≤90∘)
几点总结
- 谐振峰值 M r M_r Mr、相角裕度 γ \gamma γ和超调量 δ \delta δ都是关于阻尼比 ξ \xi ξ的单调函数；四者已知任意一个可以知道其他三个
- 超调量 δ \delta δ只与相角裕度 γ \gamma γ(谐振峰值 M r M_r Mr)有关
- 调节时间 t s t_s ts与剪切频率 ω c \omega_c ωc(带宽频率 ω b \omega_b ωb)和相角裕度 γ \gamma γ(谐振峰值 M r M_r Mr)都有关
- 剪切频率 ω c \omega_c ωc(带宽频率 ω b \omega_b ωb)与阻尼比 ξ \xi ξ和 ω n \omega_n ωn均有关
- 通常是已知开环传函或者闭环传函，求系统时域性质
- 剪切频率 ω c \omega_c ωc和带宽频率 ω b \omega_b ωb在一个数量级上，可替换