“30分钟”带你走进线性回归的世界，轻松学习互联网营销推荐算法！

前言

本章主要介绍用于推荐系统的算法-线性回归算法的推导介绍，文章思路如下：由机器学习介绍，到监督学习，并重点介绍监督学习中回归问题里面的线性回归问题及推导。

可能需要大家具备一定的统计学、高数相关知识。

一、由机器学习引出

1.1 机器学习的开端

1952年，IBM的Arthur Samuel（被誉为“机器学习之父”）设计了一款可以学习的西洋跳棋程序

它能通过观察棋子的走位来构建新的模型，并用其提高自己的下棋技巧

Samuel和这个程序进行多场对弈发现，随着时间的推移，程序的棋艺变得越来越好。

1.2 学习？与机器学习

从人说起，①学习理论，从实践中总结；②在理论上推导，在实践中检验；③通过各种手段获取知识或技能的过程

那么机器怎么学习？

• 处理某个特定的任务，以大量的“经验”为基础
• 对任务完成的好坏，给予一定的评判标准
• 通过分析经验数据，任务完成得更好了

1.3 机器学习算法的分类

机器学习是关于计算机基于数据分布构建出概率统计模型，并运用模型对数据进行分析与预测的方法。按照学习数据分布的方式的不同，机器学习的主要形式有监督学习、无监督学习、半监督学习及强化学习：

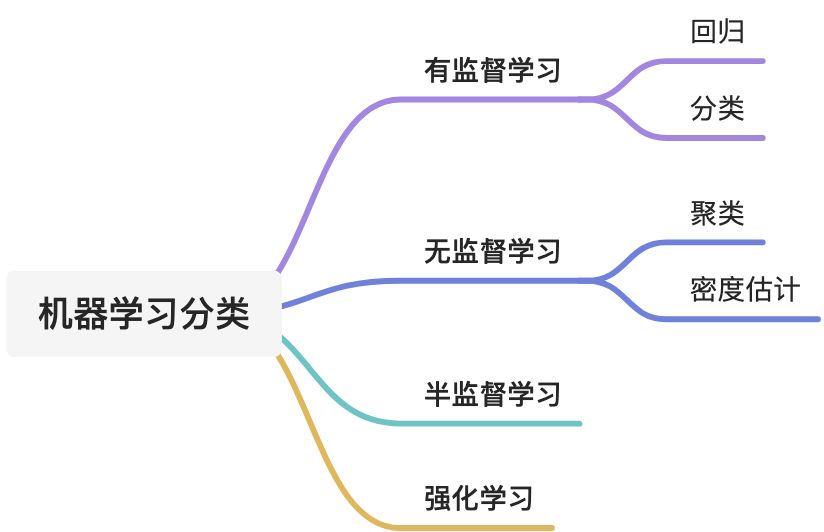
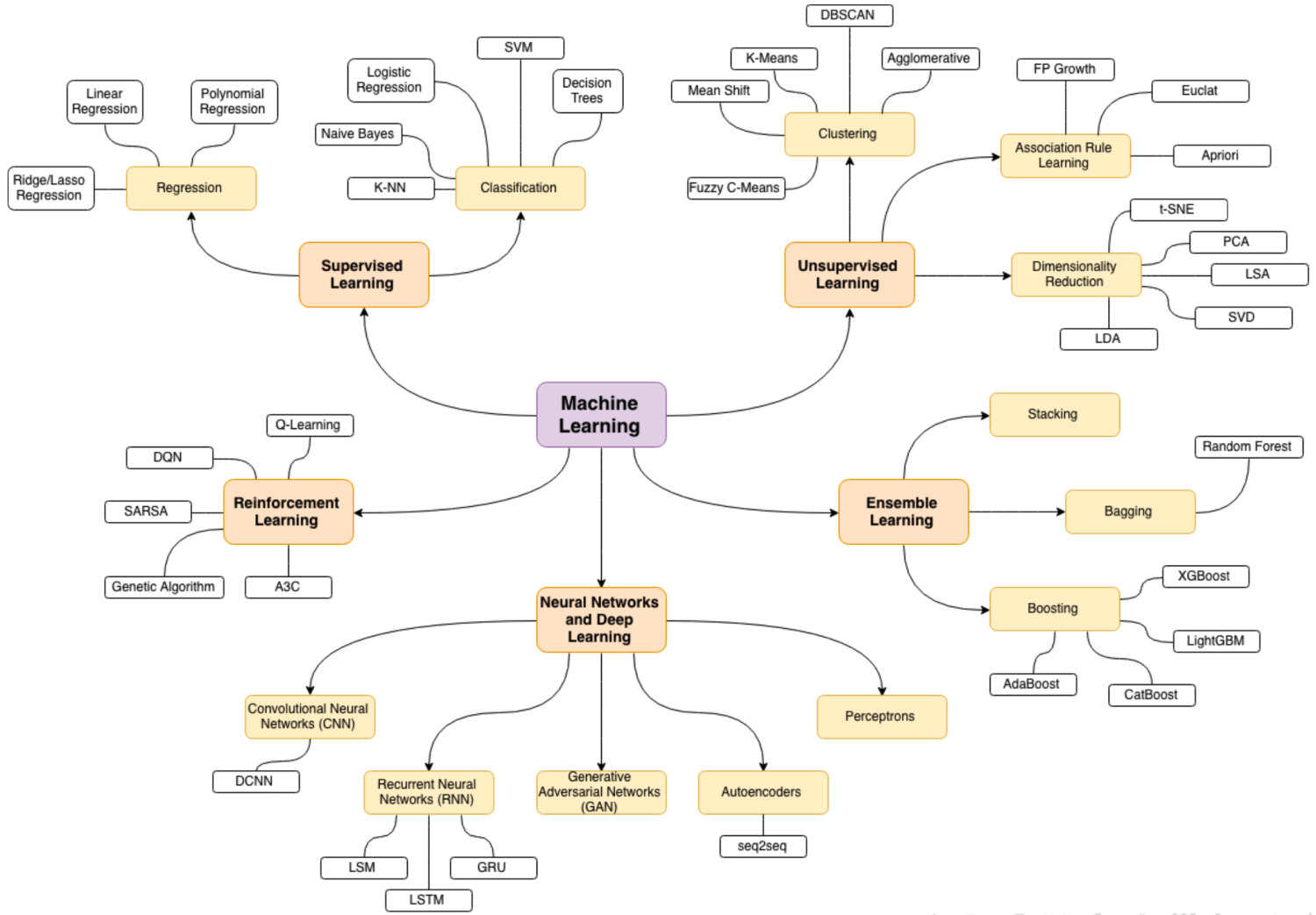
其他细分，如下图所示：

1.4 机器学习建模流程

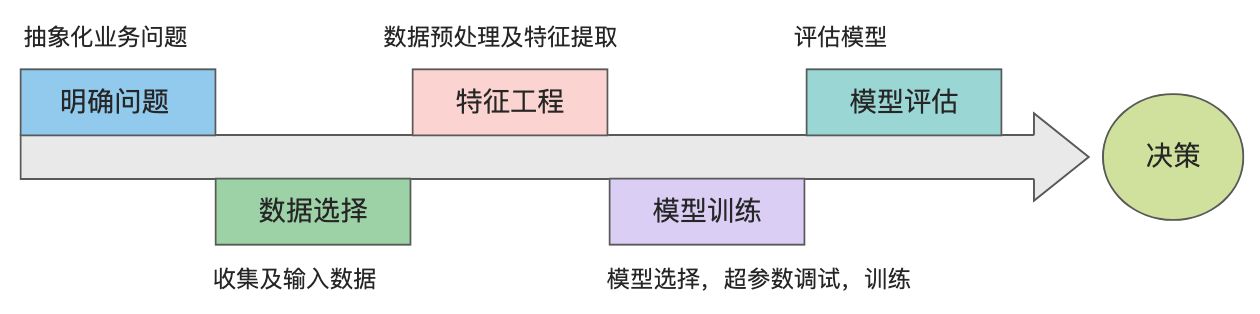
1. 明确业务问题

明确业务问题是机器学习的先决条件，这里需要抽象出现实业务问题的解决方案：需要学习什么样的数据作为输入，目标是得到什么样的模型做决策作为输出。

1. 数据选择

数据决定了机器学习结果的上限，而算法只是尽可能逼近这个上限。数据的质量决定了模型的最终效果。

1. 特征工程

特征工程就是将原始数据加工转化为模型有用的特征，包括数据预处理、特征提取

1. 模型训练

模型训练是选择模型学习数据分布的过程。这过程还需要依据训练结果调整算法的（超）参数，使得结果变得更加优良。

1. 模型评估

模型学习的目的使学到的模型对新数据能有很好的预测能力（泛化能力）。现实中通常由训练误差及测试误差评估模型的训练数据学习程度及泛化能力

1. 模型评估

决策是机器学习最终目的，对模型预测信息加以分析解释，并应用于实际的工作领域。

以上，具体不展开说明，于下回分解

1.5 监督学习介绍

有监督学习使用有标签的训练数据，“监督”可以理解为已经知道训练样本（输入数据）中期待的输出信号（标签）。

监督学习过程是，先为机器学习算法提供打过标签的训练数据以拟合预测模型，然后用该模型对未打过标签的新数据进行预测。

监督学习的分类

监督学习问题主要可以划分为两类，即分类问题和回归问题

• 分类问题预测数据属于哪一类别 ——离散
• 回归问题根据数据预测一个数值 ——连续

分类问题

分类问题预测数据所属的类别，分类的例子包括垃圾邮件检测、客户流失预测、情感分析、犬种检测等。

例如：根据肿瘤特征判断良性还是恶性，得到的是结果是“良性”或者“恶性”，是离散的。

相关分类(Classfication)算法：

• K近邻(K-NN)
• 朴素贝叶斯(Naive Bayes)
• 逻辑回归(Logistic Regression)
• 支持向量机(SVM)
• 决策树(Decision Trees)

回归问题

回归问题根据先前观察到的数据预测数值，回归的例子包括房价预测、股价预测、身高-体重预测等。

例如：预测房价，根据样本集拟合出一条连续曲线。

相关回归(Regression)算法：

• 线性回归(Linear Regression)
• 多项式回归(Polnomial Regression)
• 岭/Lasson回归(Ridge/Lasson Regression)

二、回归问题之线性回归(Linear Regression)

2.1 由问题回归问题引入

举个例子：我们需要分析下银行贷款额度受哪些因素影响？

经过特征工程后提取特征（工资和年龄），共2个特征，影响银行贷款，如下数据：

工资	年龄	额度
4000	25	20000
8000	30	70000
5000	28	35000
7500	33	50000
12000	40	85000

目标：预测银行会贷给我多少钱（标签）

考虑：工资和年龄都会影响贷款的结果，那么他们各自有多大的影响？（参数）

拟合方程

 

误差项-损失函数

 

 

 

参数求解

 

 

 

 

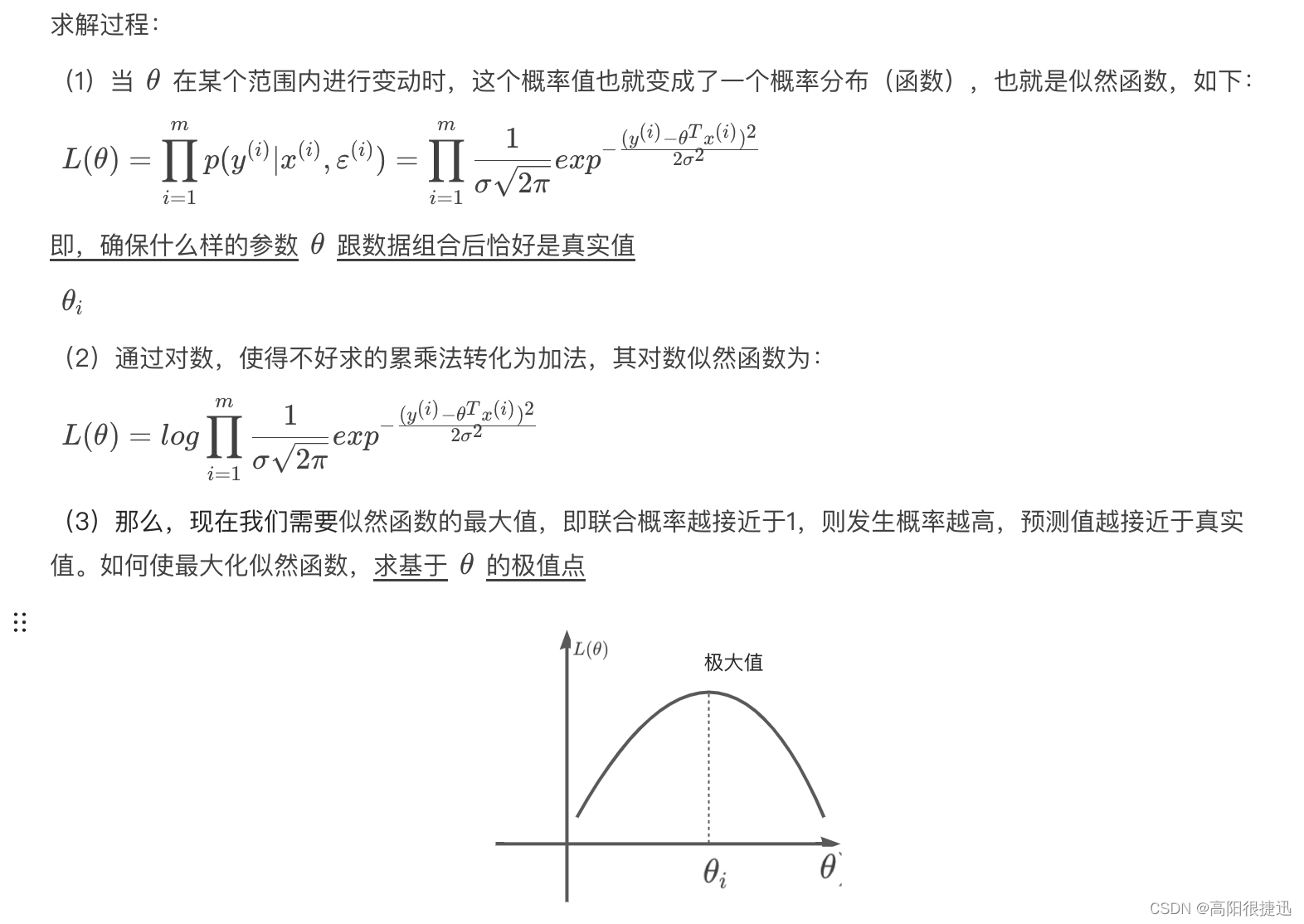
2.2 最小二乘法

 

 

 

2.3 梯度下降

2.3.1 引入

2.3.2 梯度下降介绍

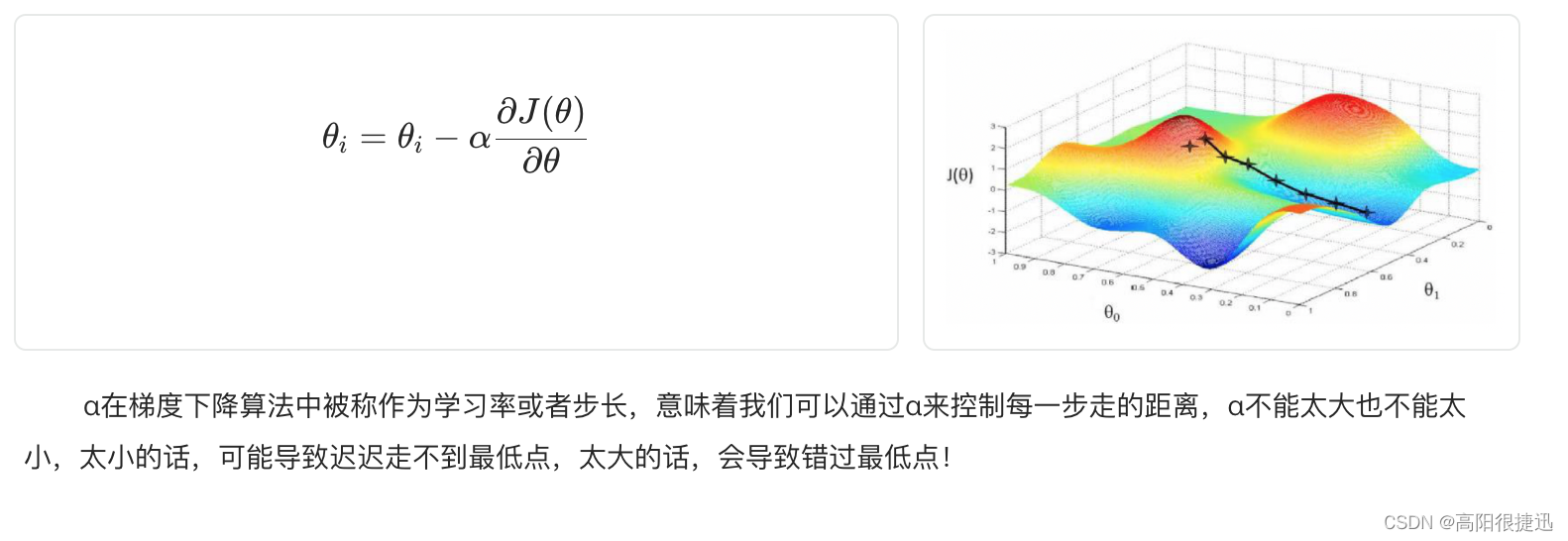
α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

（5）梯度下降思想

中心思想为：迭代地调整参数从而使成本函数最小化

首先使用一个随机的θ值(随机初始化)，然后逐步改进，每次踏出一步，每一步都尝试降低一点成本函数(如MSE)，直到算法收敛出一个最小值。学习步长与成本函数的斜率成正比，因此，当参数接近最小值时，步长逐渐变小

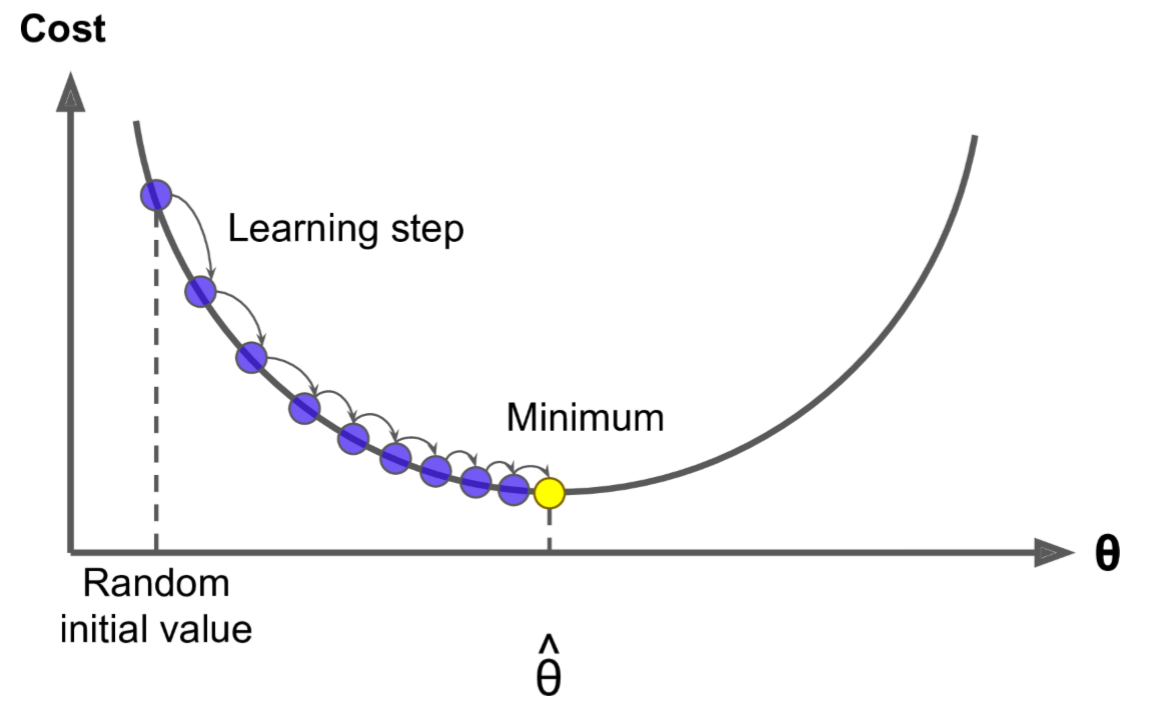
若学习率太低，算法需要经过大量迭代才能收敛

若学习率太高，则有可能比之前的起点还要高，这会导致算法发散，值越来越大

（6）梯度下降的两个主要挑战

该图显示了梯度下降的两个主要挑战：

• 梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解
• 如果损失函数是凸函数，梯度下降得到的解就不一定是全局最优解

2.3.3 梯度下降与正规方程对比

有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力.

梯度下降	正规方程（如最小二乘法）
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

2.3.4 梯度下降分类

梯度下降法有三种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。

批量梯度下降

（1）对目标函数求偏导：

（2）每次迭代对参数进行更新：

容易得到最优解，但是由于每次考虑所有样本，速度很慢

随机梯度下降

它的具体思路是：算法中对Theta的每次更新不需要再全部遍历一次整个样本，只需要查看一个训练样本进行更新，之后再用下一个样本进行下一次更新，像批梯度下降一样不断迭代更新。

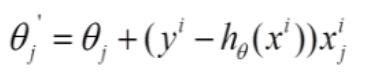
总结：每次找一个样本，迭代速度快，但不一定每次都朝着收敛的方向

小批量梯度下降法

每次更新选择一小部分数据来算，实用！

2.4 其他：牛顿和拟牛顿法

牛顿法（Netwton method）

拟牛顿法（quasi Newton method）

• 牛顿法需要求解目标函数的海塞矩阵的逆矩阵，从而大大简化了计算过程
• 拟牛顿法通过正定矩阵近似海塞矩阵的逆矩阵，从而大大简化了计算过程

三、算法实现

3.1 最小二乘法

准备数据：data.csv

代码实现：

import numpy as np
import matplotlib.pyplot as plt

# 1、导入数据
points = np.genfromtxt('data.csv', delimiter=',')
# 提取points中的两列数据，分别作为x，y
x = points[:, 0]
y = points[:, 1]

# 用plt画出散点图
plt.scatter(x, y)
plt.show()

# 2. 定义损失函数
# 损失函数是系数的函数，另外还要传入数据的x，y
def compute_cost(w, b, points):
    total_cost = 0
    M = len(points)
    
    # 逐点计算平方损失误差，然后求平均数
    for i in range(M):
        x = points[i, 0]
        y = points[i, 1]
        total_cost += ( y - w * x - b ) ** 2
    
    return total_cost/M

# 先定义一个求均值的函数
def average(data):
    sum = 0
    num = len(data)
    for i in range(num):
        sum += data[i]
    return sum/num

# 3.定义核心拟合函数
def fit(points):
    M = len(points)
    x_bar = average(points[:, 0])
    
    sum_yx = 0
    sum_x2 = 0
    sum_delta = 0
    
    for i in range(M):
        x = points[i, 0]
        y = points[i, 1]
        sum_yx += y * ( x - x_bar )
        sum_x2 += x ** 2
    # 根据公式计算w
    w = sum_yx / ( sum_x2 - M * (x_bar**2) )
    
    for i in range(M):
        x = points[i, 0]
        y = points[i, 1]
        sum_delta += ( y - w * x )
    b = sum_delta / M
    
    return w, b

# 4.测试
w, b = fit(points)

print("w is: ", w)
print("b is: ", b)

cost = compute_cost(w, b, points)

print("cost is: ", cost)

# 5.画出拟合曲线
plt.scatter(x, y)
# 针对每一个x，计算出预测的y值
pred_y = w * x + b

plt.plot(x, pred_y, c='r')
plt.show()

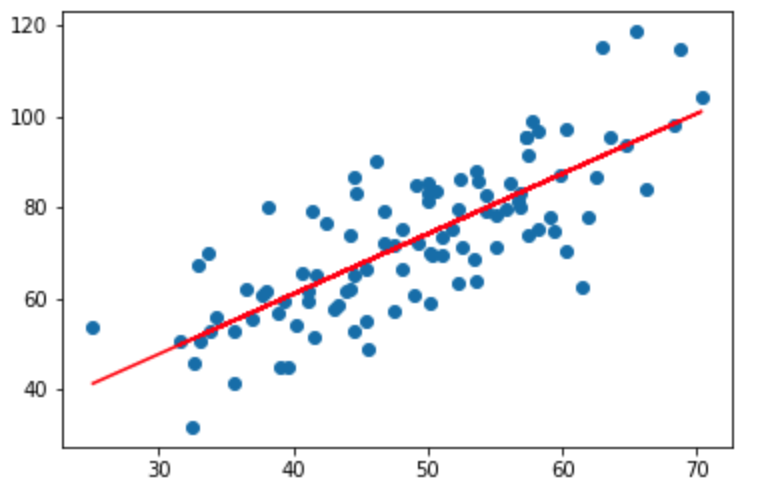
图形如下：

3.2 梯度下降

下面通过实例来应用梯度下降算法找到y=x^2+1的最小值。

算法流程：

1. 定义自变量初始值x1
2. 函数在x1处求梯度，参数更新（找最陡峭的下一点x2）
3. 函数在x2处求梯度，参数更新(找最陡峭的下一点x3)
4. 不断迭代，直到约等最小值（到达谷底）

#### 1-1 加载依赖库，定义函数
import numpy as np
import matplotlib.pyplot as plt
# 定义 y=x^2+1 函数
def function(x):
    x = np.array(x)
    y = x ** 2 + 1
    return y

####1-2 定义参数的初始值
#指定自变量更新的次数（迭代的次数）
epochs = 50
# 指定学习率的值
lr = 0.1
# 对自变量的值进行初始化
xi = -18

####1-3 求解梯度，更新参数，不断训练。
# 求取函数的梯度值
def get_gradient(x):
    gradient = 2 * x
    return gradient
# 用于存储每次自变量更新后的值
trajectory = []
# 利用梯度下降算法找到使得函数取最小值的自变量的值x_star
def get_x_star(xi):
    for i in range(epochs):
        trajectory.append(xi)
        xi = xi - lr * get_gradient(xi)
    x_star = xi
    return x_star
# 运行get_x_star函数
get_x_star(xi)


#####1-4 进行显示
x1 = np.arange(-20, 20, 0.1)
y = function(x1)
# 画出函数图像
plt.plot(x1, y)
x_trajectory = np.array(trajectory)
y_trajectory = function(trajectory)
# 画图更新过程中的自变量与其对应的函数的值
plt.scatter(x_trajectory, y_trajectory)
plt.show()

显示图形如下：

四、基于sklearn的线性回归应用

线性回归是处理一个或者多个自变量和因变量之间的关系，然后进行建模的一种回归分析方法。如果只有一个自变量的情况称为一元线性回归，如果有两个或两个以上的自变量，就称为多元回归。在sklearn中linear_model 模块几乎集成了所有线性模型，采用linear_model 中的可以实现linearRegression线性回归。

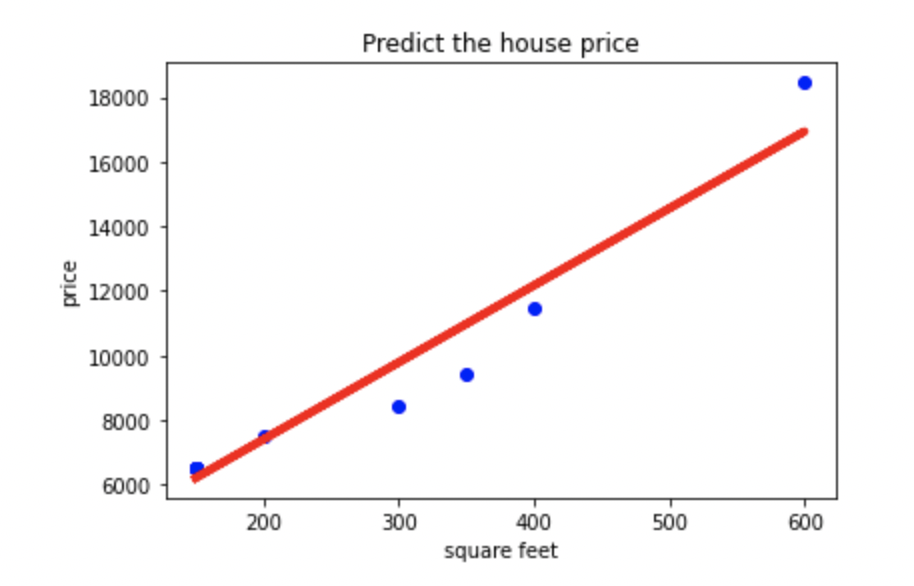
案例：找出房屋面积关于房价的拟合直线y=ax+b，根据房屋面积进行房价的预测。

准备数据：

代码如下：

#1-1导入相应的数据模块
import sys
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

# 从csv文件中读取数据，分别为：X列表和对应的Y列表
def get_data(file_name):
    # 1. 用pandas读取csv
    data = pd.read_csv(file_name)
    print('data', data)
    # 2. 构造X列表和Y列表
    X_parameter = []
    Y_parameter = []
    for single_square_feet,single_price_value in zip(data['square_feet'],data['price']):
        X_parameter.append([float(single_square_feet)])
        Y_parameter.append([float(single_price_value)])
    return X_parameter,Y_parameter

# 1-2导入相应的基础训练数据集
X,Y = get_data('./house_price.csv')

# 1-3 绘图
regr = LinearRegression() # 构造回归对象
regr.fit(X,Y)
predict_outcome = regr.predict([[700]]) # 获取预测值,预测700平方英尺大小的房子的房价

# 预测线信息
print(regr.intercept_) # 截距值
print(regr.coef_) # 回归系数（斜率值）
print(predict_outcome) # 预测值

plt.scatter(X,Y,color = 'blue') # 绘出已知数据散点图
plt.plot(X,regr.predict(X),color = 'red',linewidth = 4) # 绘出预测直线
plt.title('Predict the house price')
plt.xlabel('square feet')
plt.ylabel('price')
plt.show() # 展示图像

效果如下：

梯度下线的应用

# 随机梯度下降
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler

# 归一化数据
std = StandardScaler()
std.fit(X_train)
X_train_std = std.transform(X_train)
X_test_std = std.transform(X_test)

# n_iter代表浏览多少次，默认是5
sgd_reg = SGDRegressor(n_iter=100)
sgd_reg.fit(X_train_std, y_train)
sgd_reg.score(X_test_std, y_test)