主要记录一下On预处理,O1取任意区间前缀和的前缀和
题目

解题思路
贪心从小到大考虑,每次计算以 a i a_i ai为最小值时的贡献。
下面来看具体例子:
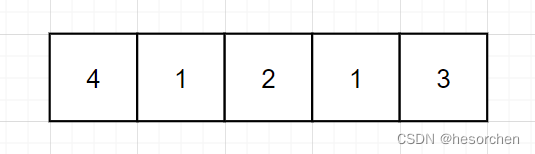
- 考虑 a 2 a_2 a2作为最小值时的贡献
区间 [ 1 , 2 ] , [ 1 , 3 ] , [ 1 , 4 ] , [ 1 , 5 ] , [ 2 , 2 ] , [ 2 , 3 ] , [ 2 , 4 ] , [ 2 , 5 ] [1,2],[1,3],[1,4],[1,5],[2,2],[2,3],[2,4],[2,5] [1,2],[1,3],[1,4],[1,5],[2,2],[2,3],[2,4],[2,5] - 考虑 a 4 a_4 a4作为最小值时的贡献
区间 [ 3 , 4 ] , [ 4 , 4 ] , [ 4 , 5 ] , [ 3 , 5 ] [3,4],[4,4],[4,5],[3,5] [3,4],[4,4],[4,5],[3,5]
如果我们计算区间 [ 1 , 4 ] [1,4] [1,4]或 [ 2 , 4 ] [2,4] [2,4],则与1中的贡献计算发生了重复。因此每次计算 a i a_i ai的贡献时,左端点不超过上个值与 a i a_i ai相同的位置,右端点到 n n n,但是,这样还不够,我们还要保证这些区间的最小值为 a i a_i ai。 - 考虑 a 3 a_3 a3作为最小值时的贡献
区间 [ 3 , 3 ] [3,3] [3,3]合法,因为之前枚举过的 a i a_i ai都小于当前值,会分割数组。
接下来考虑如何计算区间贡献。我们不可能枚举所有区间,这样会超时,来观察上述步骤1中的贡献情况。
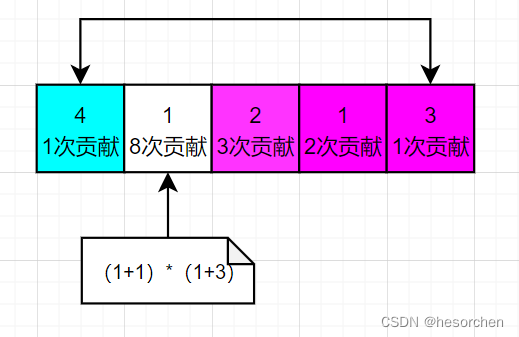
容易发现,以 a i a_i ai为最小值的时候,左边元素的贡献次数为 1 次 , 2 次 , 3 次 . . . . . . 1次,2次,3次... ... 1次,2次,3次......,左边元素的贡献次数为 . . . . . . 3 次 , 2 次 , 1 次 ... ...3次,2次,1次 ......3次,2次,1次, a i a_i ai本身贡献次数为 ( n u m l e f t + 1 ) × ( n u m r i g h t + 1 ) (num_{left}+1)\times(num_{right}+1) (numleft+1)×(numright+1)次。只需要确定区间的左右端点,就可以直接计算以 a i a_i ai为最小值的所有区间的贡献。
a i a_i ai两侧的贡献次数,满足前缀和的前缀和规律。右侧部分是从左向右的前缀和的前缀和。左侧部分是从右向左的后缀和的后缀和。如何快速计算任意区间的前缀和的前缀和呢?
来看下图。
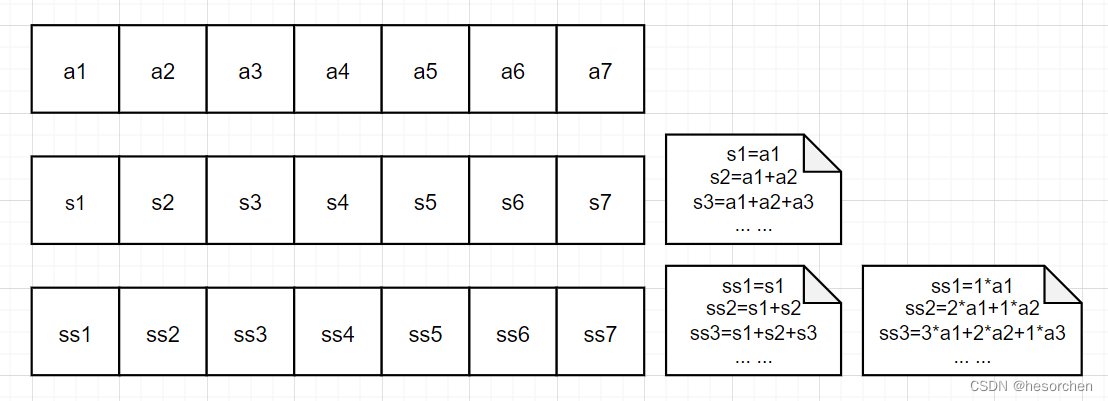
初始化 : s 0 = s s 0 = 0 s_0 = ss_0=0 s0=ss0=0
前缀和: s i = s i − 1 + a i s_i = s_{i-1}+a_i si=si−1+ai
前缀和的前缀和: s s i = s s i − 1 + s i ss_i = ss_{i-1}+s_i ssi=ssi−1+si
结论:
s s l , r = s s r − s s l − 1 − ( r − l + 1 ) × s l − 1 ss_{l,r}=ss_{r}-ss_{l-1}-(r-l+1)\times s_{l-1} ssl,r=ssr−ssl−1−(r−l+1)×sl−1
很容易验证结论的正确性,不再赘述。
这样一来,我们就可以 O ( n ) O(n) O(n)预处理之后, O ( 1 ) O(1) O(1)得到任意区间的前缀和的前缀和。
后缀同理。
AC代码
const long long N = 1e5 + 5;
const long long mod = 1e9 + 7;
class Solution
{
public:
map<long long, vector<long long>> pos;
long long pre[N], suf[N], ppre[N], ssuf[N];
set<long long> st;
set<long long> vis;
long long n;
void init_ss(vector<int> &a)
{
int n = a.size() - 1;
for (int i = 1; i <= n; i++)
pre[i] = pre[i - 1] + a[i];
for (int i = 1; i <= n; i++)
ppre[i] = (ppre[i - 1] + pre[i]) % mod;
for (int i = n; i >= 1; i--)
suf[i] = suf[i + 1] + a[i];
for (int i = n; i >= 1; i--)
ssuf[i] = (ssuf[i + 1] + suf[i]) % mod;
}
long long getlr(int l, int r)
{
long long len = r - l + 1;
return (ppre[r] - (ppre[l - 1] + pre[l - 1] * len) % mod + mod) % mod;
}
long long getrl(int r, int l)
{
long long len = r - l + 1;
return (ssuf[l] - (ssuf[r + 1] + suf[r + 1] * len) % mod + mod) % mod;
}
long long totalStrength(vector<int> &a)
{
n = a.size();
a.insert(a.begin(), -1);
init_ss(a);
vis.insert(0);
vis.insert(n + 1);
for (long long i = 1; i <= n; i++)
{
st.insert(a[i]);
pos[a[i]].emplace_back(i);
}
long long ans = 0;
for (auto val : st)
{
long long m = pos[val].size();
for (long long i = 0; i < m; i++)
{
long long p = pos[val][i];
auto iter = vis.upper_bound(p);
long long rr = (*iter) - 1;
iter--;
long long ll = (*iter) + 1;
long long lenL = p - ll + 1;
long long lenR = rr - p + 1;
long long num, v;
num = lenL;
v = getlr(p, rr);
ans = (ans + num * v % mod * val) % mod;
num = lenR;
v = getrl(p, ll);
ans = (ans + num * v % mod * val) % mod;
num = lenR * lenL % mod;
v = val;
ans = (ans - num * v % mod * val % mod + mod) % mod; //减去重复贡献
vis.insert(p);
}
}
return ans;
}
};