搬运的一些动态规划题目（C++实现）

1、连续子数组的最大和

来源：剑指offer面试题31

题目，输入一个整形术组，数组里有整数也有负数，数组中一个或连续的多个整数组成一个子数组，求所有子数组的和的最大值，要求时间复杂度为O(n)

例子：int arr[] = {1,-2,3,10,-4,7,2,-5};
在遍历整个数组的过程中，我们可以发现数组中每一个数字为子数组尾部（假设长度为m），对应的子数组和，都是和前面m-1个数字的和有关系的，这就说明子问题之间是有重复计算的更小的子问题（子问题重叠）【重叠的子问题我们要申请数据结构或者用题目中原有的数据结构来保存以防止重复计算】，并且大问题的最优解也是由子问题的最优解组合而成的（最优自结构），所以我们可以很明显知道这可以用动态规划的思想来解。

分析此题可知，如果当前数字之前子数组的和为负数的话，那么之前的和加上当前数字的值反而变小了，如例子中1+(-2)=-1，那么如果3再加入此数组，和从3开始一个新的数组，和反而变小了（变为2），那么我们当然从3开始重新计算啦。这说明f(n-1)<=0的时候，我们是放弃之前的数组和的。否则我们会继续进行累加。可得公式如下：

f (i) = {\begin{matrix} d a t a [i] & i = 0 o r f (i - 1) <= 0 \\ f (i - 1) + d a t a [i] & i > 0 a n d f (i - 1) > 0 \end{matrix}

$f(i)=\left\{\begin{matrix} data[i] & i=0 {\color{Red} o\color{Red}r} f(i-1)<=0\\ f(i-1)+data[i] &i>0 {\color{Red} a\color{Red}n\color{Red}d} f(i-1)>0 \end{matrix}\right.$
代码如下：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        if(array.empty())
            return 0;
        if(array.size() == 1)
            return array[0];
        int cur = array[0];//cur变量存储子数组的和
        int ret = array[0];//用来记录计算过程中出现过的最大和
        for(int i = 1; i < array.size(); ++i){
            //cur = max(cur+array[i], array[i]);    //二者都可，下一行更清晰体现公式
            cur = cur > 0 ? cur+array[i] : array[i];
            ret = max(ret, cur);
        }
        return ret;
    }
};

int main()
{
    int arr[] = {1,-2,3,10,-4,7,2,-5};
    //int arr[] = {-2,-8,-1,-5,-9};
    vector<int> vec(arr, arr + sizeof(arr)/sizeof(int));
    Solution sl;
    int ret = sl.FindGreatestSumOfSubArray(vec);
    cout << ret << endl;

    return 0;
}


#endif

2、数字三角形

来源：数字三角形

          7
        3   8
      8   1   0
    2   7   4   4
  4   5   2   6   5

在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。只需要求出这个最大和即可，不必给出具体路径。三角形的行数大于1小于等于100，数字为 0 - 99

要求输出最大和
接下来，我们来分析一下解题思路：
首先，肯定得用二维数组来存放数字三角形

[7][ ][ ][ ][ ]
[3][8][ ][ ][ ]
[8][1][0][ ][ ]
[2][7][4][4][ ]
[4][5][2][6][5]

然后我们用D( r, j) 来表示第r行第 j 个数字(r,j从1开始算)
我们用MaxSum(r, j)表示从D(r,j)到底边的各条路径中，最佳路径的数字之和。
因此，此题的最终问题就变成了求 MaxSum(1,1)
可得公式如下：

f (i, j) = m a x (f (i + 1, j), f (i + 1, j + 1)) + d a t a [i] [j]

$f(i,j)=max(f(i+1,j), f(i+1,j+1))+data[i][j]$
最后一行的最优解就是本身，所以可以得到最后一行的最优解为：

[4][5][2][6][5]

倒数第二行在最后一行的基础上，不停累加并始终记录每一个数字的最大值（每一个数字对应两条路线，选出自身的最大值即可）。

[7][12][10][10][ ]

循序计算，最终得到：

[30][  ][  ][  ][  ]
[23][21][  ][  ][  ]
[20][13][10][  ][  ]
[ 7][12][10][10][  ]
[ 4][ 5][ 2][ 6][ 5]

然而其实我们不需要重新开辟数组对中间所有的和进行计算，我们只需要保留最新的和就行，即每次都保存要计算的行的下一行的最优解就可以。并且我们还可以使用题中所给数组的最后一行进行数值的保存，即每次更新最后一行的值。
代码如下：

#include <iostream>
#include <algorithm>
using namespace std;

#define MAX 101
int D[MAX][MAX];
int n;
int *maxsum;

int main()
{
    int i, j;
    int n;//例子数组
    n = 5;
    D[1][1] = 7;
    D[2][1] = 3;
    D[2][2] = 8;
    D[3][1] = 8;
    D[3][2] = 1;
    D[3][3] = 0;
    D[4][1] = 2;
    D[4][2] = 7;
    D[4][3] = 4;
    D[4][4] = 4;
    D[5][1] = 4;
    D[5][2] = 5;
    D[5][3] = 2;
    D[5][4] = 6;
    D[5][5] = 5;
    maxsum = D[n];
    for(i = n - 1; i >= 1; i--)
        for(j = 1; j <= i; j++)
            maxsum[j] = max(maxsum[j], maxsum[j+1]) + D[i][j];
    cout << maxsum[1] << endl;

    return 0;
}

3、环路加油站问题

来源：算法：C++实现动态规划中的几个典型问题

有一个环路,中间有N个加油站,加油站里面的油是g1,g2…gn,加油站之间的距离是d1,d2…dn,从加油站g(i)到g(i+1)耗费的汽油是d(i),问其中是否能找到一个加油站,使汽车从这个加油站出发,走完全程。如果存在满足条件的加油站，返回该加油站的序号,否则返回-1。
主要就是变形成为查找是否有一个n长的前缀和全大于0的序列。

这道题和之前的连续字数组最大和问题其实是非常类似的，题意是让我们在一个环形的数组中，找到一个序列，可以使我们在走到每一个加油站的时候，车上的油量都是大于等于0的，这就满足了可以开到每个加油站的理想了！换成术语来说，就是要求我们每走到序列中的一个数字的时候，子数组前缀和都大于等于0。

我们直接申请两倍长的数组，将同一个数组重复存入就可以得到环形数组中的每一个序列，例如数组1，2，3，只需申请有六个位置的数组，存入1，2，3，1，2，3，就可以遍历得到1，2，3；2，3，1；3，1，2这三个序列。

刚才说了，前缀和必须大于0，这就指导我们如果出现了前缀和小于0的情况时，之前的子数组就不能再用了，从当前开始，否则就继续累加和，直到出现长度为原数组长度（就是加油站数量）的序列。
公式如下：

f (i {\begin{matrix} d a t a [i] & i = 0 o r f (i - 1) < 0 \\ f (i - 1) + d a t a [i] & i > 0 a n d f (i - 1) >= 0 \end{matrix}) =

$f(i\left\{\begin{matrix} data[i] & i=0 {\color{Red} o\color{Red}r} f(i-1)<0\\ f(i-1)+data[i] & i>0 {\color{Red} a\color{Red}n\color{Red}d} f(i-1)>=0 \end{matrix}\right.)=$
代码就很好写了：

#include <iostream>
#include <vector>  
using namespace std;  

int selectGasStation(const vector<int> &a, const vector<int> &g) {  
    vector<int> line(a.size()<<1);  

    int n=line.size();  
    for(int i=0;i<n;i++)  
        line[i]=a[i%a.size()]-g[i%a.size()];  

    int start=0;    //记录起点
    int oil=0;      //记录前缀和
    for(int i=0;i<n;i++)  
    {  
        if ( oil<0 )    //前缀和小于0，就换用当前节点作为起点
        {  
            start=i;  
            oil=line[i];  
        }  
        else  //n=0或者后续前缀和大于0的时候，都持续累加 说明车子还能继续走（油没空）
        {  
            oil+=line[i];     
            if ( i-start>=a.size() )  
                return start;  
        }  
    }  
    return -1;  
} 

int main()
{
    int arr2[] = {1,2,6,5,5,6,7};   //加油站距离
    int arr1[] = {2,2,3,8,2,9,9};   //汽油
    vector<int> a(arr1, arr1+7);
    vector<int> g(arr2, arr2+7);
    int s = selectGasStation(a, g);
    cout << s << endl;

    return 0;
}

4、查找暗黑串

来源：算法：C++实现动态规划中的几个典型问题

一个只包含’A’、’B’和’C’的字符串，如果存在某一段长度为3的连续子串中恰好’A’、’B’和’C’各有一个，那么这个字符串就是纯净的，否则这个字符串就是暗黑的。
例如：BAACAACCBAAA 连续子串”CBA”中包含了’A’,’B’,’C’各一个，所以是纯净的字符串。AABBCCAABB 不存在一个长度为3的连续子串包含’A’,’B’,’C’,所以是暗黑的字符串。你的任务就是计算出长度为n的字符串(只包含’A’、’B’和’C’)，有多少个是暗黑的字符串。

这道题找到公式的过程比较麻烦，首先我们假设前n-1个字串已经排列好了（暗黑串），这样这个串是否为暗黑串就和第n位有关，第n位和前两位组成了连续的A、B、C，就变成了纯净串，对于这个排列好的串，可能性为f(n-1)，那么对于最后一个要放进去的字母来说，有多少种（f(n)）可能，取决于前面的两个字母是什么样的排列，前两个字母相同，也可能不相同。

可以知道f(n-1)最后两位要么是相同，要么是不同（same是末尾两字母相同的数量，diff是末尾两字母不同的数量）：

f (n - 1) = s a m e (n - 1) + d i f f (n - 1)

$f(n-1)=same(n-1)+diff(n-1)$
对于f(n)，当f(n-1)末尾两字母相同的时候，f(n)可以任意取值，生成的都是暗黑串，当f(n-1)末尾两字母不同的时候，f(n)可以取两字母中任意一个，这样不会生成纯净串。即：

f (n) = 3 * s a m e (n - 1) + 2 * d i f f (n - 1)

$f(n)=3*same(n-1)+2*diff(n-1)$
两公式计算得到：

f (n) = 2 * f (n - 1) + s a m e (n - 1)

$f(n)=2*f(n-1)+same(n-1)$
现在我们要知道diff和f之间的关系，才可以得到一个递推公式，首先我们知道在公式

f (n) = 3 * s a m e (n - 1) + 2 * d i f f (n - 1)

$f(n)=3*same(n-1)+2*diff(n-1)$
中，same的3种情况，有1种是末尾两个字母相同的，例如：AAA，AAB，AAC中的AAA末尾两个字母相同，diff的2种情况中，有1种是末尾两个字母相同的，例如：ABA，ABB中的ABB末尾两字母相同，所以我们可以得出：

s a m e (n) = s a m e (n - 1) + d i f f (n - 1)

$same(n)=same(n-1)+diff(n-1)$
所以可以得出：

s a m e (n) = f (n - 1) => s a m e (n - 1) = f (n - 2)

$same(n)=f(n-1)=>same(n-1)=f(n-2)$
（这里还有一个简单的理解可以得到same(n=f(n-1))，因为f(n-1)无论有多少种可能（暗黑串），只要第n位和其相同，就是same(n)，并且一定是暗黑串）
故得出递推公式

f (n - 1) = 2 * f (n - 1) + f (n - 2)

$f(n-1)=2*f(n-1)+f(n-2)$
由此可以写出代码：

#include <iostream>
#include <vector>  
using namespace std;  
int main()
{
    int n;
    cout << "input n:";
    cin >> n;
    vector<unsigned long> num(n+1);
    num[0] = 3; //A、B、C三种可能
    num[1] = 9; //AA、AB、AC、BA、BA、BC、CA、CB、CC九种可能
    //开始执行公式
    for(int i = 2; i < n; i++)
        num[i] = 2 * num[i-1] + num[i-2];
    cout << num[n-1] << endl;


    return 0;
}

5、袋鼠过河

来源：算法：C++实现动态规划中的几个典型问题

一只袋鼠要从河这边跳到河对岸，河很宽，但是河中间打了很多桩子，每隔一米就有一个，每个桩子上都有一个弹簧，袋鼠跳到弹簧上就可以跳的更远。每个弹簧力量不同，用一个数字代表它的力量，如果弹簧力量为5，就代表袋鼠下一跳最多能够跳5米，如果为0，就会陷进去无法继续跳跃。河流一共N米宽，袋鼠初始位置就在第一个弹簧上面，要跳到最后一个弹簧之后就算过河了，给定每个弹簧的力量，求袋鼠最少需要多少跳能够到达对岸。如果无法到达输出-1

示例输入：
5
2 0 1 1 1
示例输出：
4
此题一是每个桩的步数是由前面的桩的步数计算得到的，一个是桩和桩的步数之前存在重复的子问题，所以我们是可以通过动态规划解出来的。

对于每一个桩i，读取桩上的弹簧力量，就可以知道它可以达到的下一个桩是哪些（i+1~i+j），更新这些桩的步数（当前桩所指步数加1），但是由于这些要更新的桩（i+1~i+j），可能被i之前的桩更新过，所以要进行比较，记录最小的路程。
公式如下：

r e t [i + j] = m i n (r e t [i + j], r e t [i]);

$ret[i+j]=min(ret[i+j],ret[i]);$

#include <iostream>
#include <vector>  
using namespace std;  
int main()
{
    int n;
    cin >> n;
    vector<int> vec(n, 0);  //记录弹簧力量
    vector<int> ret(n, 10000);  //记录到当前桩的步数
    int hops = -1;  //跳过河流的最小步数
    ret[0] = 1; //初始化第0个桩（河宽度为0）
    for(int i = 0;  i < n; ++i)
        cin >> vec[i];

    //开始进行公式的运算
    //遍历整个河流上的树桩，对每一个树桩上的ret值进行修改，选择最小的
    for(int i = 0; i < n; ++i){
        for(int j = 1; j <= vec[i]; ++j){
            if(i + j < n)   //当前桩跳不到对岸
                ret[i+j] = min(ret[i] + 1, ret[i+j]);//1、从ret的步数再加一步可以跳到这里；2、之前记录过的跳到这里的步数；2选1，选择小的
            else //当前桩可以跳到对岸
                if(hops == -1)  //还没有初始化最小步数
                    hops = ret[i] == 10000 ? -1 : ret[i];   //如果是没有走到过的桩，那么是不能经由这个桩跳到对面的，否则就初始化hops为步数
                else //已经初始化过步数了
                    hops = min(hops, ret[i] + 1);   //如果没初始化，ret[i]+1>=10001，肯定是比较大的那个
        }
    }
    cout << hops << endl; 

    return 0;
}

6、合唱团问题

来源：每日N刷——动态规划（2017网易内推题，合唱团，C++实现）

描述：有 n 个学生站成一排，每个学生有一个能力值，牛牛想从这 n 个学生中按照顺序选取 k 名学生，要求相邻两个学生的位置编号的差不超过 d，使得这 k 个学生的能力值的乘积最大，你能返回最大的乘积吗？

输入：每个输入包含 1 个测试用例。每个测试数据的第一行包含一个整数 n (1<=n<= 50)，表示学生的个数，接下来的一行，包含 n 个整数，按顺序表示每个学生的能力值 ai（-50 <= ai <= 50）。接下来的一行包含两个整数，k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出：输出一行表示最大的乘积。

本题首先要分析，如果知道了前k-1个同学能力的最大值，那么不就可以轻易得到k个同学的能力最大值了吗？
所以这是一个递推的问题。

对于每一个节点来说，既有可能是k个同学中的最后一个，也有可能是k个同学的中间一个（除去边界情况），所以为了得到最大乘积，我们要记录每个同学作为k个同学中的第1~k个的最大乘积，这样一共n个同学就需要n*k个空间，所以可以采用二维数组的方式。假设有5个同学（能力值是7，3，5，2，6），最多可以选择3人的话，设置的数组如下：

[7][3][5][2][6]
[X][ ][ ][ ][X]
[X][X][ ][ ][ ]

“X”所代表的部分都是边界条件，所以我们只要循序计算，把这个表格填上，然后对表格的最后一行取最大值即可（最后一行为当前数字作为第k个数的乘积）。

但是我们仔细审题，可以知道能力值是可以为负数的，这样就不一定是之前的最大值乘当前数得到的还是最大值，因为当前数可能是负数，而之前乘积为负数，可能通过这个负数，改头换面成为最大值，为了避免漏算负数的情况，我们要把最小值也包含在内，并在每次计算的时候都取之前最小值，最大值和当前值计算的两个结果中的较大值。
知道了这样的思路，我们就可以很容易写出代码：

#include <iostream>
#include <vector>  
using namespace std; 
int main()
{
    int number; //学生数量
    cin >> number;
    vector<int> ability(number + 1);    //学生能力数组
    for(int n = 1; n <= number; ++n)
        cin >> ability[n];
    int choose; //选择的学生数量
    cin >> choose; 
    int interval;   //学生最大间隔
    cin >> interval;
    long ret = 0;
    //最大和最小是为了应对要放进去的数是正数还是负数（负负得正可能会产生更大的正整数）
    //fm[k][i]表示当选中了k个学生，并且以第i个学生为结尾，所产生的最大乘积,第一行就是当前所在的位置的值
    vector<vector<long> > fm(choose + 1, vector<long>(number + 1, 0));//存储最大能力乘积
    vector<vector<long> > fn(choose + 1, vector<long>(number + 1, 0));//存储最小能力乘积
    int cnt, i, j;
    for(cnt = 1; cnt <= number; ++cnt){ //遍历整个数组，每个位置上的数作为选中的k个学生中的1~k个位置的乘积都要求出来
        fm[1][cnt] = fn[1][cnt] = ability[cnt]; //作为第1个数的时候不用计算，直接写进去就行
        for(i = 2; i <= choose; ++i){ //作为队列第i个数时
            for(j = cnt - 1; j > 0 && cnt - j <= interval; --j){
                //把队列之前的作为第i-1的数（这个数和现在的数距离不能超过给定值）的乘积都乘一下，并放进数组中第i行
                //状态转移方程
                fm[i][cnt] = max(fm[i][cnt], max(fm[i-1][j] * ability[cnt], fn[i-1][j] * ability[cnt]));
                fn[i][cnt] = min(fn[i][cnt], min(fm[i-1][j] * ability[cnt], fn[i-1][j] * ability[cnt]));
            }
        }
        ret = max(ret, fm[i-1][cnt]);   //保存曾经的最大值
    }
    cout << ret << endl;

    return 0;
}

7、钢条切割

来源：1、算法导论-动态规划-钢条切割
2、【算法笔记】动态规划，三个例题（解题思路与C++代码）

Serling公司购买长钢条，将其切割为短钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。假定我们知道Serling公司出售一段长为i英寸的钢条的价格为pi(i=1,2,…，单位为美元)。钢条的长度均为整英寸。图15-1给出了一个价格表的样例。

长度	1	2	3	4	5	6	7	8	9	10
价格	1	5	8	9	10	17	17	20	24	30

钢条切割问题是这样的：给定一段长度为n英寸的钢条和一个价格表pi(i=1,2,…n)，求切割钢条方案，使得销售收益rn最大。注意，如果长度为n英寸的钢条的价格pn足够大，最优解可能就是完全不需要切割。

最简单的方法就是使用递归的方法，但是这种递归的方法会重复计算很多内容，假设我们将一段长度为4的钢条分为2段长度为2的部分，那么第一次和第二次计算，虽然都是长度为2，但是毫无关系。递归代码不列出。

如何减少重复的计算量呢？使用一个数组来保存中间值无疑是最常用的方法。

首先我们需要申请一个长度为n+1的数组（设传入的钢条长度为n）来保存所有计算的中间量，还是刚才说的例子，第一次计算了长度为2的钢条收益最大为5后，第二次直接在辅助的数组中读出这个值，不需要再次计算，这样在进行递归计算的时候，就不会进行重复计算了。

很明显这是从大问题往小问题拓展，先计算的是大问题，然后划分为小问题，通过小问题的计算来完善大问题的值。使用的是递归的思想。这种方法成为带备忘的自顶向下计算方法
代码如下：

int cut(const vector<int> input, int length, vector<int> &ret)
{
    if (ret[length] >= 0)
        return ret[length];//首先检查所需的值是否存在

    int profit = -1;
    if (length == 0)
        profit = 0;
    else
        for (int i = 1; i <= length; ++i)
            profit = max(profit, input[i] + cut(input, length - i, ret));
    ret[length] = profit;

    return profit;
}

int MemoizedCutRod(const vector<int> input, int length)
{
    vector<int> r(length+1, -1);
    return cut(input, length, r);
}
int main()
{
    int arr[] = { 0,1,5,8,9,10,17,17,20,24,30 };
    vector<int> table(arr, arr+11);
    int ret = MemoizedCutRod(table, 4);
    cout << ret << endl;
    return 0;
}

除了可以自顶向下计算，还可以转换思路，自底向上计算（计算的思想类似于斐波那契数列），首先我们需要得出长度为1的最优解，然后以此为依据，计算得出长度为2的最优解…最后得出最优解。

int main()  
{  
    int arr[] = { 0,1,5,8,9,10,17,17,20,24,30 };
    vector<int> table(arr, arr+11); 
    int n;  
    cin >> n;//输入钢条长度  
    vector<int> ret(n+1,0);//数组下标从1开始，初始化11位数组  
    ret[1] = 1;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= i; j++)
            ret[i] = max(ret[i], table[j] + ret[i-j]);
    }  
    cout << ret.back() << endl;
    return 0;
}

8、装备线调度

来源：动态规划之装配线调度理解

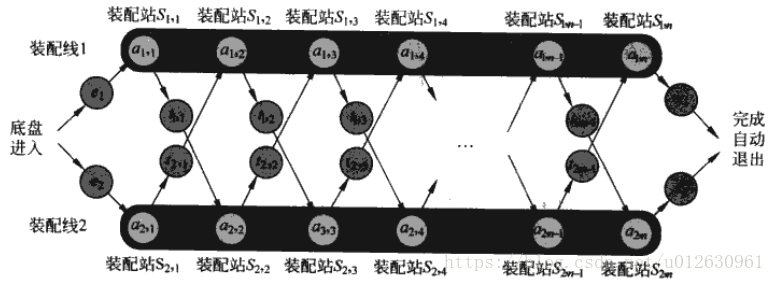
Colonel汽车公司在有两条装配线的工厂内生产汽车。一个汽车底盘在进入每一条装配线后，在一些装配站中会在底盘上安装部件，然后，完成的汽车在装配线的末端离开。每一条装配线上有n个装配站，编号为j=1,2,…,n。将装配线i（i为1或2）的第j个装配站表示为。装配线1的第j个站（）和装配线2的第j个站（）执行相同的功能。然而，这些装配站是在不同的时间建造的，并且采用了不同的技术，因此，每个站上所需的时间是不同的，即使在两天不同装配线相同位置的装配站上也是这样。把在装配站上所需的装配时间记为。底盘进入装配线i的进入时间为ei，装配完的汽车离开装配线i的离开时间为xi。
正常情况下，一旦一个底盘进入一条装配线后，它只会经过该条装配线。在相同的装配线中，从一个装配站到下一个装配站所花的时间可以忽略。偶尔会来一个特别急的订单，客户要求尽可能快地制造这些汽车。对这些加急的订单，底盘仍然依序经过n个装配站，但工厂经理可以将部分完成的汽车在任何装配站上从一条装配线移到另一条装配线上。把已经通过装配站的一个底盘从装配线i移走所花的时间为，其中i=1,2，j=1,2,…,n-1（因为在第n个装配站后，装配已经完成）。问题是要确定在装配线1内选择哪些站以及在装配线2内选择哪些站，以使汽车通过工厂的总时间最小。

装配线图

题目很长，但是题意非常简单，就是要在两条装配线中选择一条合适的曲折路线（就是在两条装配线中来回倒腾），使最后装配的时间最短，并且进入装配线和退出装配线都是有时间消耗的，这里我们还是可以理解到一个子问题重叠，每个节点的装配时间来源于之前节点的装配时间的较小值加上本身的装配时间；其次就是最优子结构，这个问题的最优解很明显在整条装配路线上一直是最优解，也就是子问题是最优解。

观察图，进入装配线和退出装配线的时间分别为 $e1，e2，x1，x2$ ,在装配线上转移的时间为 $t_{i,j}$ （i代表第i条装配线，j代表运往另外一条装配线的第j个装配站）,在装配站上耗费的时间为 $a_{i,j}$ （第i条装配线的第j个装配站）。

很明显，这些值都是要输入的，我们输入的例子是：

    vector<int> a1 = { 7,9,3,4,8,4 };//初始化各节点的时间消耗    
    vector<int> a2 = { 8,5,6,4,5,7 };
    vector<vector<int> > work;
    work.push_back(a1);
    work.push_back(a2);
    vector<int> t12 = { 2,3,1,3,4 };
    vector<int> t21 = { 2,1,2,2,1 };
    vector<vector<int> > transport;
    transport.push_back(t12);
    transport.push_back(t21);
    vector<tuple<int, int> > path;
    int e1 = 2;
    int e2 = 4;
    int x1 = 3;
    int x2 = 2;

转换成类似上图即为：
实例图
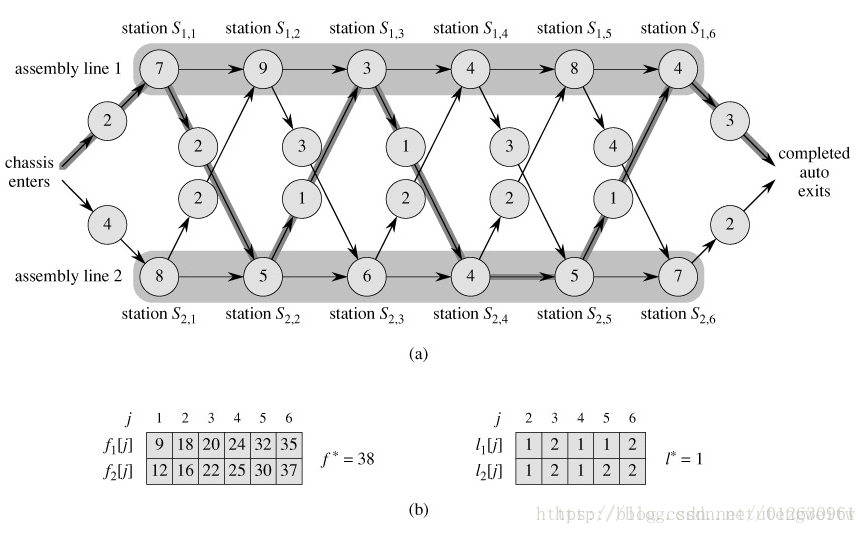
图来源：【算法导论】动态规划算法之装配线调度

所以可以很轻松得到公式为：

f_{1} [j] = {\begin{matrix} e_{1} + a_{1, 1} & j = 1 \\ m i n (f_{1} [j - 1] + a_{1, j}, f_{2} [j - 1] + t_{2, j - 1} + a_{1, j})) & j >= 2 \end{matrix}

$f_{1}[j]=\left\{\begin{matrix} e_{1}+a_{1,1} & j = 1\\ min(f_{1}[j-1]+a_{1,j}, f_{2}[j-1]+t_{2,j-1}+a_{1,j})) & j >=2 \end{matrix}\right.$

f_{2} [j] = {\begin{matrix} e_{2} + a_{2, 1} & j = 1 \\ m i n (f_{2} [j - 1] + a_{2, j}, f_{1} [j - 1] + t_{1, j - 1} + a_{2, j})) & j >= 2 \end{matrix}

$f_{2}[j]=\left\{\begin{matrix} e_{2}+a_{2,1} & j = 1\\ min(f_{2}[j-1]+a_{2,j}, f_{1}[j-1]+t_{1,j-1}+a_{2,j})) & j >=2 \end{matrix}\right.$
代码如下：

//本代码使用了部分C++11语法，需要编译器支持
#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>
using namespace std;

int findPath(vector<vector<int> > &work, vector<vector<int> > &transport, vector<tuple<int, int> > &path, int trans1, int trans2, int put1, int put2)
{
    vector<int> f1(6, 0);
    vector<int> f2(6, 0);
    //vector<tuple<int, int> > path;
    int ret = 0;
    f1[0] = trans1 + work[0][0];
    f2[0] = trans2 + work[1][0];
    path.push_back(f1[0] < f2[0] ? make_tuple(1, 1) : make_tuple(2, 1));
    int i = 1;
    for ( ; i < work[0].size(); ++i) {
        f1[i] = min(f1[i - 1] + work[0][i], f2[i-1] + work[0][i] + transport[1][i - 1]);
        f2[i] = min(f2[i - 1] + work[1][i], f1[i-1] + work[1][i] + transport[0][i - 1]);
        path.push_back(f1[i] < f2[i] ? make_tuple(1, i + 1) : make_tuple(2, i + 1));
    }
    ret = min(f1[i-1] + put1, f2[i-1] + put2);
    return ret;
}

int main()
{

    vector<int> a1 = { 7,9,3,4,8,4 };//初始化各节点的时间消耗    
    vector<int> a2 = { 8,5,6,4,5,7 };
    vector<vector<int> > work;
    work.push_back(a1);
    work.push_back(a2);
    vector<int> t12 = { 2,3,1,3,4 };
    vector<int> t21 = { 2,1,2,2,1 };
    vector<vector<int> > transport;
    transport.push_back(t12);
    transport.push_back(t21);
    vector<tuple<int, int> > path;
    int e1 = 2;
    int e2 = 4;
    int x1 = 3;
    int x2 = 2;
    int lfinal = 0;//表示产品最终在哪个条线完成装配  
    lfinal = findPath(work, transport, path, e1, e2, x1, x2);
    cout << lfinal << endl;
    for (vector<tuple<int, int> >::iterator it = path.begin(); it != path.end(); ++it)
        cout << "line " << get<0>(*it) << ' ' << "station " << get<1>(*it) << endl;
    return 0;

}

未完待续

关于动态规划的一些概念性理解：
1、五大常用算法之二：动态规划算法
2、动态规划算法——知识点总结