问题:在二维平面坐标系中,对于任意一个多边形,已知其各个顶点坐标为,计算该多边形的面积。
看到“坐标”和“面积”这两个词的时候,我首先联想到的是上一篇刚写的博客内容:向量的外积。那么我们试着从向量的外积切入,看能不能解答计算面积的问题。
向量外积的定义:
如果两个向量
则=
为了便于计算推导,我们将外积定义公式再进一步演化一下,如下:
=
=
=
降维到二维平面上,我们把,得到
=
=
,其中
分别表示x轴,y轴,z轴的单位向量。
因为第3列中,除了第1行其它行都是0,所以我们根据行列式的第3列展开,得到
=
=
=
,其中
表示
的代数余子式。
所以我们在二维平面中计算两个向量的外积时,可以通过计算两个向量的坐标有序数组的行列式来求值。在上一篇博客中,我们已经验证,两个向量的外积的值的绝对值等于原点和
三个点所围成三角形的面积的2倍。
有了这个基础之后,我们再回到问题中来。
问题描述的是多边形,我们先从最简单的多边形上来找思路:三角形,如下图:
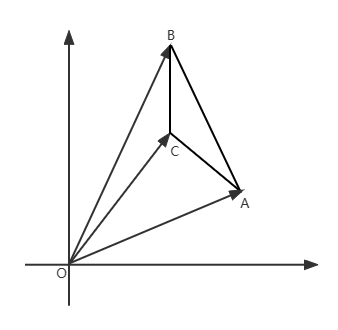
上图中三角形面积等于
我们使用向量外积来带入上面公式中的各个三角形面积,可得
=
注意:向量进行叉乘时,所得结果会有正有负,正负代表着方向,满足右手法则。
计算完三角形,我们推进一步到四边形。
四边形就变得稍微复杂了一点,因为四边形有所谓的凸边形和凹边形,我们尝试一下这两种情景是否能有一样的计算思路,即凹凸无感。我们先将两种图形分开计算。
凸边形:
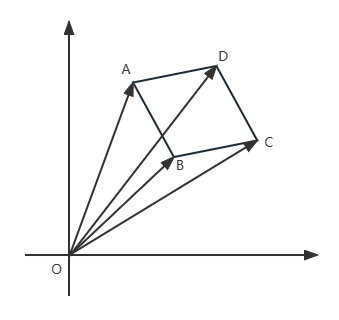
=
=
凹边形:
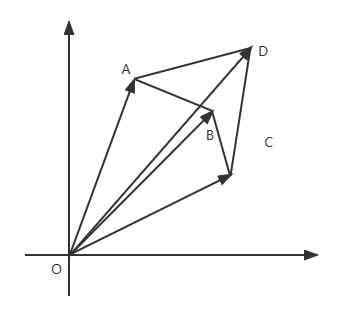
=
=
发现上下两个结果的公式是统一的,也就是四边形的凸边形和凹边形,使用向量外积进行面积计算时,计算公式是一致的,凹凸无感。
现在我们从三角形到四边形都验证了一个解题方法,就是:
多边形各个顶点与原点所组成的向量,按照逆时针顺序(或者顺时针也可以),依次前后两个向量作叉乘求外积,尾首向量也得叉乘,(换一种说法,就是说图形中每条边相连的两个端点之间需要进行首尾叉乘),然后将所有外积相加求和所得的二分之一的绝对值,就是这个多边形的面积。即
=
这个计算方法是否可以应用到所有多边形?我们通过数学归纳法来求证一下。
假设n条边时,=
是成立的,那么此时在此基础上增加一个点
,变成n+1条边时
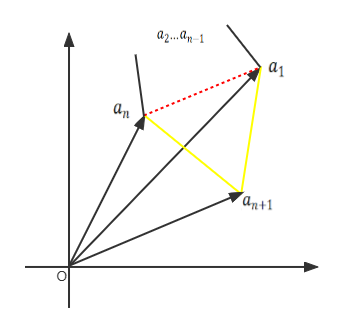
如上图,我们需要增加两条边(图中黄色部分),去除
这条边(图中红色虚线),那么
= +
= +
(注:此处对应着增加两条边和去除一条边)
=
最终结果是满足我们上面总结的计算规则的。至此,我们从理论上得到了多边形面积的解法。
那么接下来,我们就需要把这个计算方法移植到计算机上,让计算机替我们执行计算,所以我们需要继续把计算公式演化成计算机方便计算的形式。
=
=
=
=
其中,当时,
,即
最终,我们得到了上面的公式,就是著名的Shoelace Theorem鞋带定理。
它有什么特点呢?我们借用一下网络上的图片,如下:
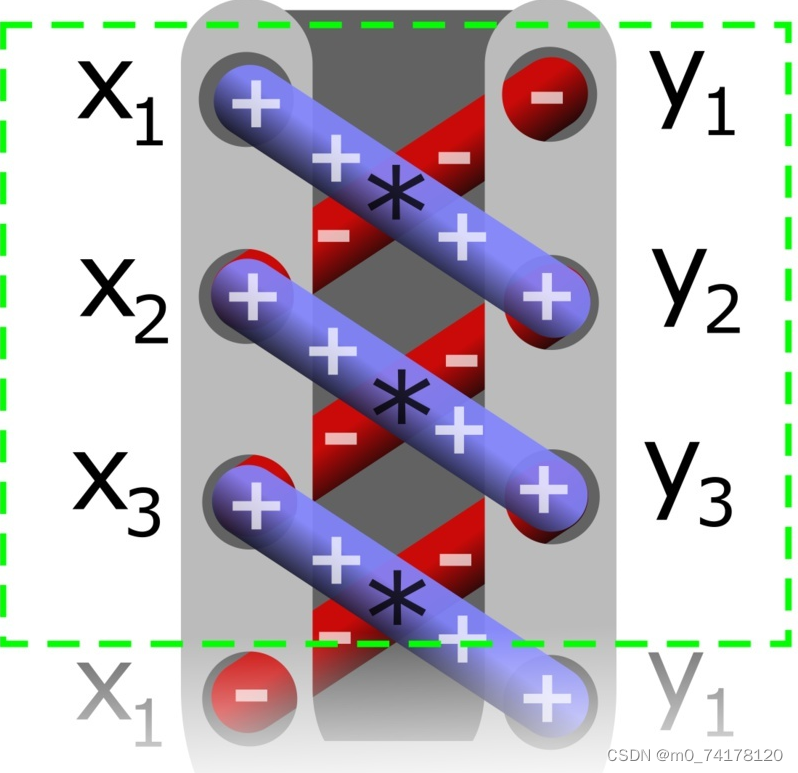
因为这个公式的运算很像鞋带,所以被称为鞋带定理。
有了鞋带定理,我们就可以轻松移植成代码了。
struct Point2d
{
double x;
double y;
Point2d(double xx, double yy): x(xx), y(yy){}
};
//计算任意多边形的面积,顶点按照顺时针或者逆时针方向排列
double ComputePolygonArea(const vector<Point2d> &points)
{
int point_num = points.size();
if(point_num < 3)return 0.0;
double s = 0;
for(int i = 0; i < point_num; ++i)
s += points[i].x * points[(i+1)%point_num].y - points[i].y * points[(i+1)%point_num].x;
return fabs(s/2.0);
}