1. OTFS输入输出关系的矩阵表示

1.1 OTFS：矩阵表示

1.2 OTFS发射机的实现

1.2.1 传统的OTFS调制

1. OTFS输入输出关系的矩阵表示

1.1 OTFS：矩阵表示

发送符号的时频域表示：DD域上的ISFFT+海森堡变换+波束整形

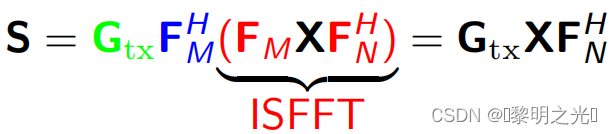
向量形式：

接受符号的DD域表示：时频域上的波束整形+维格纳变换+SFFT

向量形式

1.2 OTFS发射机的实现

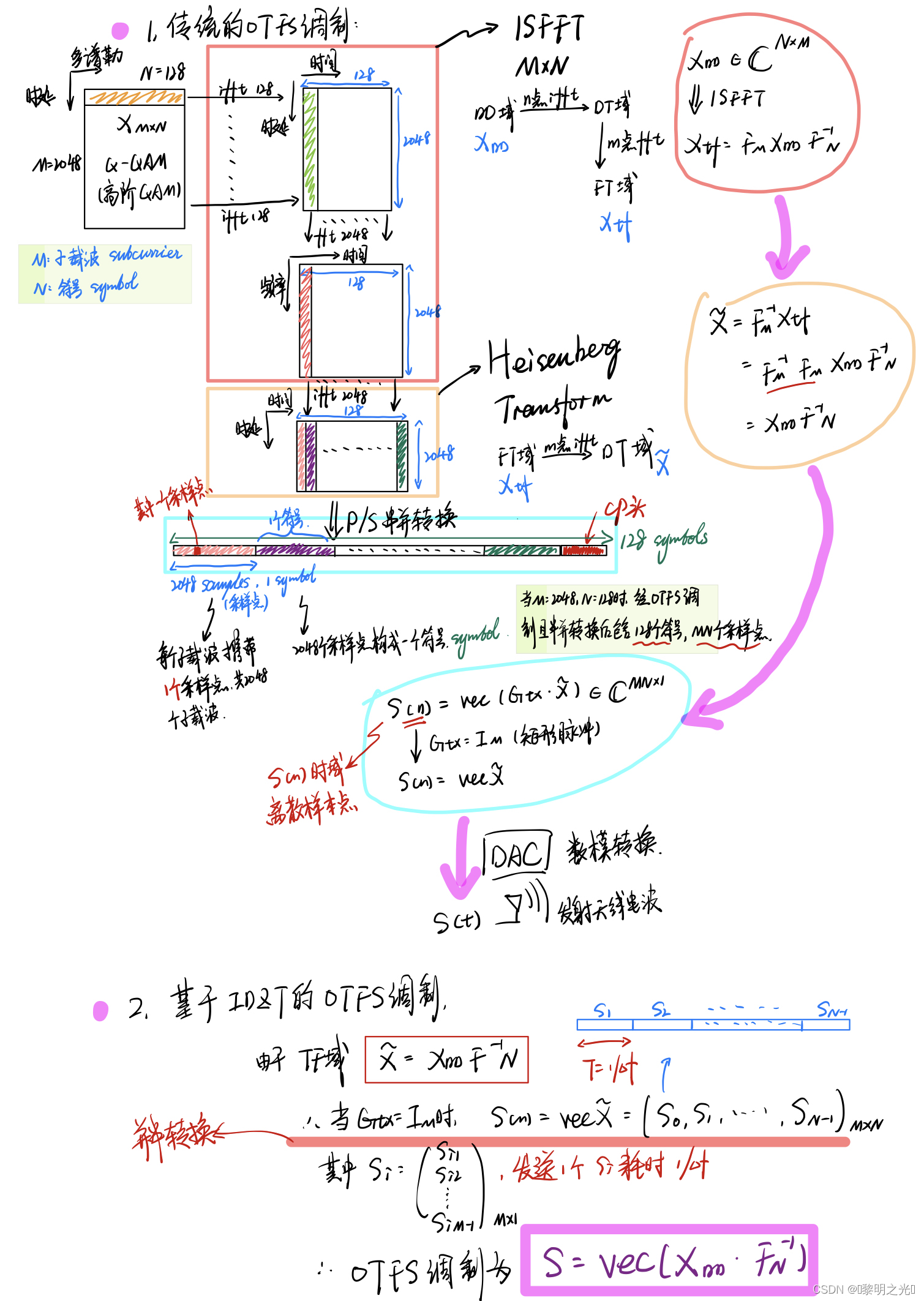
1.2.1 传统的OTFS调制

M=2048，N=128，其中M表示number of delay bins（subcarriers）N表示number of doppler bins（time slots）即symbols

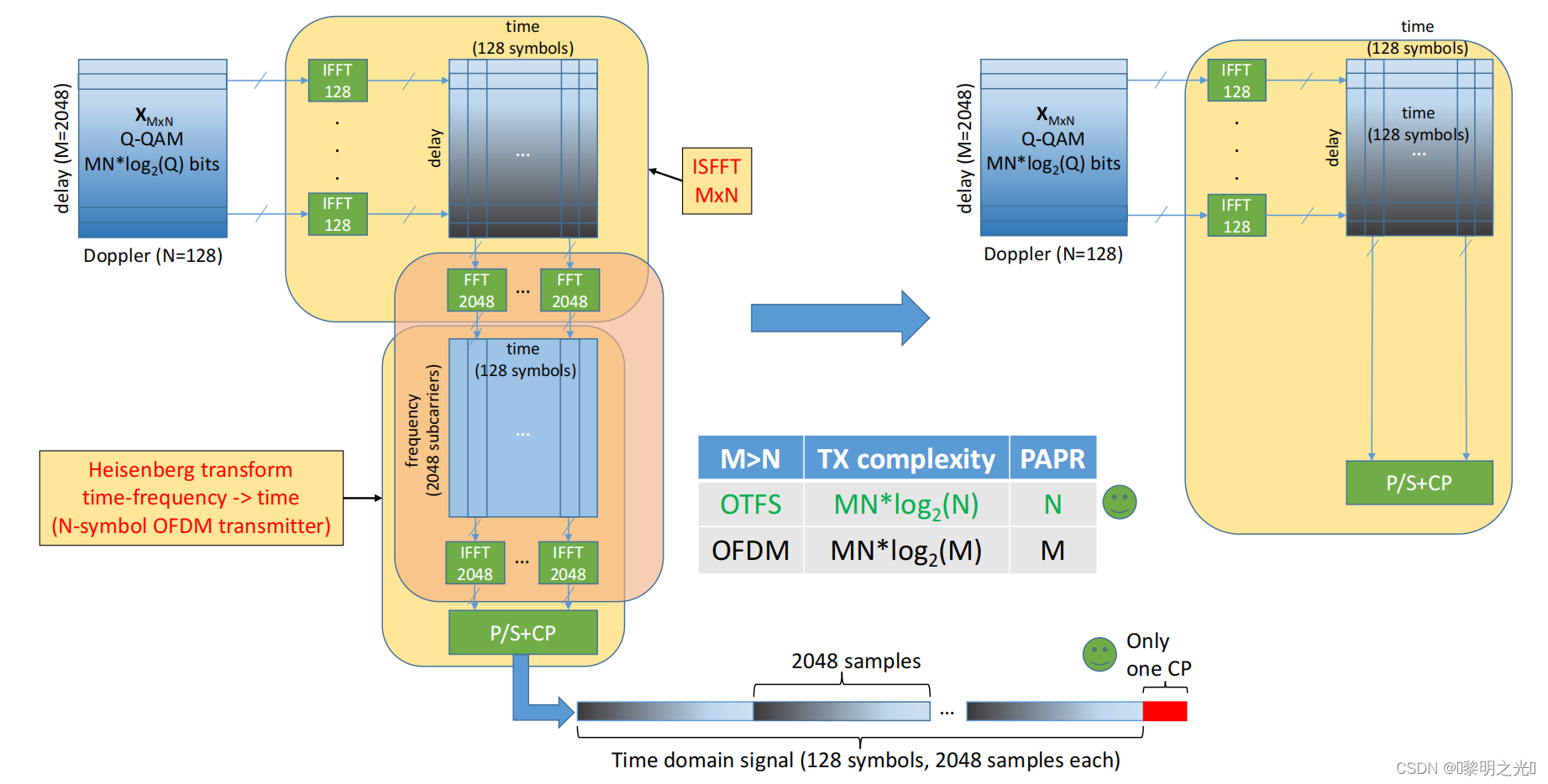
发射机过程如上图左侧所示（右侧的是IDZT即传统OTFS调制的升级版，后面讲）：

ISFFT

首先将高阶QAM调制符号 $\chi$ 放置在DD域的M*N二维网格中 $\chi\in\mathbb{C}^{N*M}$ ，采用正辛有限傅里叶逆变换（ISFFT）将DD域符号 $\chi$ 转换为TF域符号 $\chi _{tf}\in\mathbb{C}^{M*N}$ ，变换过程如下：

沿每个多普勒轴的n点ifft $F_{N}^{-1}$ 和沿每个时延轴的m点fft $F_{M}$

$\chi _{tf}=F_{M}\cdot \chi \cdot F_{N}^{-1}$

【公式1.2.1】

海森堡变换

接着对时频域矩阵 $\chi _{tf}$ 进行海森堡变换即通过m点ifft $F_{M}^{-1}$ 转换为延迟时间域（delay-time）的样本矩阵 $\tilde{\chi }\in \mathbb{C}^{M*N}$ 公式表示为下式：

$\tilde{\chi }=F_{M}^{-1}\cdot \chi _{tf}=F_{M}^{-1}\cdot F^{M}\cdot \chi \cdot F_{N}^{-1}=\chi \cdot F_{N}^{-1}$

【公式1.2.2】

我们可以发现 $F_{M}^{-1}\cdot F^{M}$ 等价于一个单位阵，因此最后的海森堡变换和上一步ISFFT中的沿时延轴的fft相抵消，简化成了一个离散的Zak变换inverse discrete Zak transform (IDZT)，即右侧图像表示的那样：只需要经过沿多普勒轴的n点ifft。

通过对延迟时间矩阵 $\tilde{\chi }$ 进行发射机脉冲整形，然后进行行向量化，得到NM长度时域样本向量s

【公式1.2.3】

公式1.2.2和1.2.3为一个完整的海森堡变换，然后将时域样本向量s进行DA转换，并以s (t)的形式传输到无线介质中。

其中，对角矩阵Gtx有gtx(t)的样本作为其主对角元素

对于矩形波形，它简化为M×M单位矩阵

1.2.2 基于IDZT的OTFS调制

如下图所示，OTFS调制相当于一个IDZT，将延迟-多普勒域的X转换为延迟-时域的 $\tilde{\chi }$ 。假设发射的为矩形脉冲整形波形，M=8，N=6。

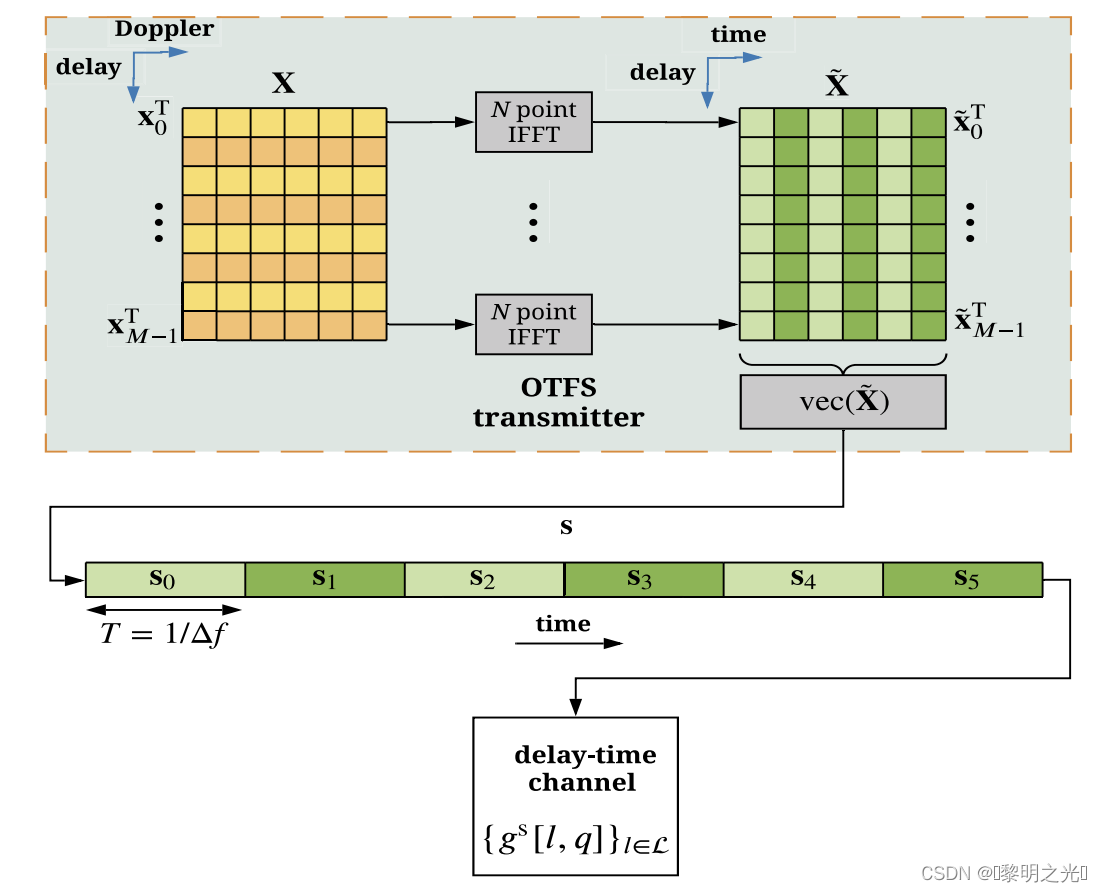
在图中，延迟多普勒矩阵和延迟时间矩阵被分割为向量 $x_{m}\in \mathbb{C}^{N\times 1}$ 和 $\tilde{x}_{m}\in \mathbb{C}^{N\times 1}$ 。

对公式1.2.2进行转置得到

由于IFFT的对称性，IFFT的转置等于本身，然后经过并行到串行转换后，如Gtx = IM，公式1.2.3的时域样本减少为

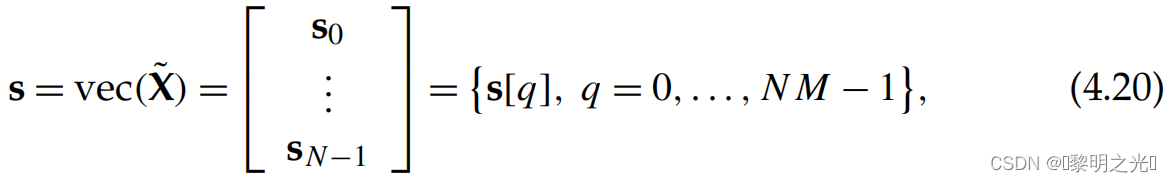
其中每一个行向量 $s_{n}\in \mathbb{C}^{M\times 1},n=0,...,N-1$ ，即每一个s包含了M个时域样本，占用 $T=1/\Delta f$ 秒的时间。

从上图中，我们可以直接将公式4.19和公式4，20中的 $\chi$ 和s关联为（Gtx为单位阵，可以去掉）

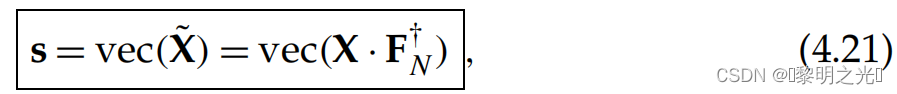
s中的元素可以表示为下式

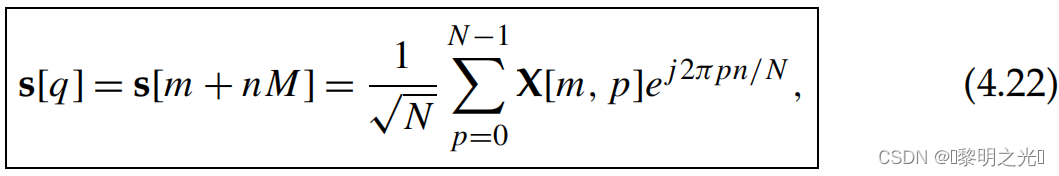
其中q=m+nM，对于m=0,...,M-1;n=0,...,N-1，这正是 $\chi$ 的IDZT变换

1.3 OTFS接收机的实现

1.3.1 传统的OTFS解调

维格纳变换

在接收端，我们得到接收到NM个复杂样本向量表示为

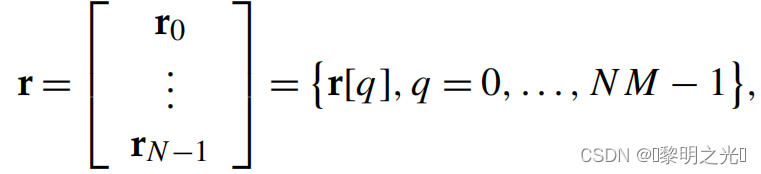
其中对于n=0,1,...,N-1来说， $r_{n}\in \mathbb{C}^{M\times 1}$ ，向量r被转换为延迟时间矩阵 $\tilde{Y}\in \mathbb{C}^{M\times N}$

其中 $vec^{-1}_{M,N}(r)$ 将 $r_{n}\in \mathbb{C}^{M\times 1}$ 转换成M*N的矩阵，同时对角阵Grx是接收机脉冲成形矩阵，由下式定义

对于矩形脉冲整形波形Grx等价于M阶单位阵，因此公式4.24简化为下式

然后，通过对延迟时间样本矩阵 $\tilde{Y}\in \mathbb{C}^{M\times N}$ 沿着时延轴进行m点DFT运算，得到时频域接收样本矩阵 $Y_{tf}$

公式（4.24）和（4.26）中的操作构成了维格纳变换。之后再执行一个SFFT操作来获得延迟-多普勒域符号。

SFFT

将矩阵 $Y_{tf}$ 沿着时延轴进行m点IDFT运算得到延迟多普勒域矩阵，沿多普勒轴进行n点DFT运算，带有维格纳变换的级联SFFT运算可以简化为

将公式4.46带入4.27可知，SFFT使用的m点IDFT与维格纳变换中的DFT相抵消，因此简化为了DZT运算

1.3.2 基于DZT的OTFS解调

如公式（4.24）和（4.27）所示，OTFS解调相当于一个DZT，将时域内接收到的样本转换为延迟多普勒域符号，下图显示了矩形脉冲整形波形Grx = IM的等效接收操作

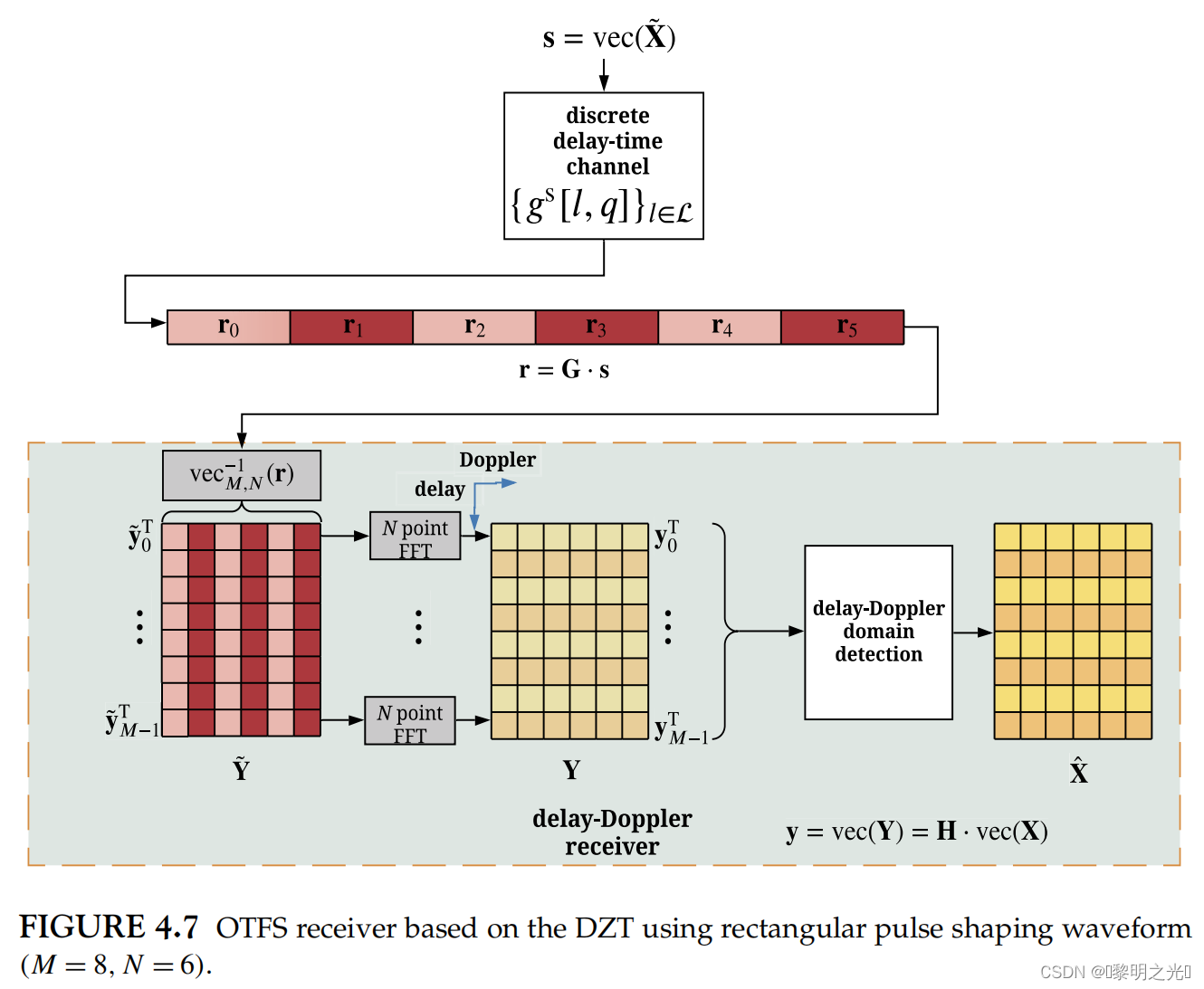
在图中，时延多普勒和延迟时间矩阵 $Y$ 和 $\tilde{Y}$ 沿着时延轴被分割成了m个向量 $y_{m}$ , $\tilde{y}_{m}\in \mathbb{C}^{N\times 1}$ ，其中每个向量都含有N个元素， m=0,1,...,M-1。

取公式（4.27）的转置（DFT的对称性使得其转置为本身）

从图4.7中，我们可以通过（4.24）和（4.28）将r和Y直接联系为

可进一步表示为矩阵元素形式

当m=0,1,...,M-1，n=0,1,...,N-1时，公式4.30即为r的DZT变换，记作 $Y=Z_{M}[r]$

参见第5章，并注意其中使用的延迟和多普勒指数为l,k遵循Zak变换常规符号，与本章中使用的m,n不同

笔者自己的理解

Appendix Matlab Code

A.OTFS参数设置

%-------------------------------------------------------
%参考1.2
%MATLAB代码1 OTFS帧参数设置
%-------------------------------------------------------

% number of Doppler bins (time slots)
N=16;
% number of delay bins (subcarriers)
M=64;
% normalized DFT matrix
Fn=dftmtx(N);
Fn=Fn/norm(Fn);
% subcarrier spacing
delta_f=15e3;
% block duration
T=1/delta_f;
% carrier frequency
fc=4e9;
% speed of light
c=299792458;
% OTFS grid delay and Doppler resolution
delay_resolution = 1/(M*delta_f);
Doppler_resolution = 1/(N*T);

B.发射机

%MATLAB code 2 Generate OTFS frame
% QAM modulation
tx_info_symbols=qammod(tx_info_bits,mod_size,’gray’,’InputType’,’bit’);
% Generate the MxN OTFS delay-Doppler frame
X=reshape(tx_info_symbols,M,N);
% Vectorized OTFS frame information symbols
x=reshape(X.’,N*M,1);
% Method 1 (Eqs. (4.19) and (4.20))
X_tilda=X*Fn’;
s=reshape(X_tilda,1,N*M);

C. 接收机

%% MATLAB code 12 OTFS demodulation
% Method 1 (Eqs. (4.24) and (4.27))
Y_tilda=reshape(r,M,N);
Y=Y_tilda*Fn;
% vectorize Y
y=reshape(Y.’,N*M,1);

注意：这是部分代码~

OTFS输入输出关系

1. OTFS输入输出关系的矩阵表示

1.1 OTFS：矩阵表示

1.2 OTFS发射机的实现

1.2.1 传统的OTFS调制

ISFFT

海森堡变换

1.2.2 基于IDZT的OTFS调制

1.3 OTFS接收机的实现

1.3.1 传统的OTFS解调

维格纳变换

SFFT

1.3.2 基于DZT的OTFS解调

笔者自己的理解

Appendix Matlab Code

A.OTFS参数设置

B.发射机

C. 接收机

猜你喜欢