三角公式
发现自己貌似学的又是假三角公式 …
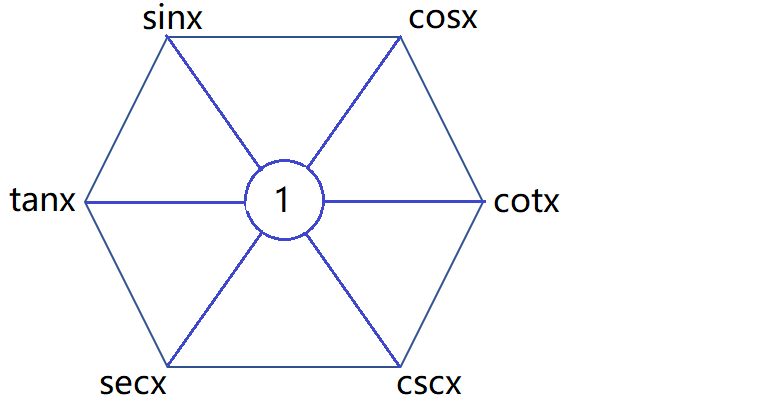
1、基本定义
设角 α \alpha α 的终边与单位圆交于点 P ( x , y ) P(x,y) P(x,y),则有
s i n α = y ; c o s α = x ; \begin{aligned}sin\alpha=y;\ \ \ cos\alpha=x;\end{aligned} sinα=y; cosα=x;
t a n α = y x ; c o t α = x y ; \begin{aligned}tan\alpha=\dfrac{y}{x};\ \ cot\alpha=\dfrac{x}{y};\end{aligned} tanα=xy; cotα=yx;
s e c α = 1 x ; c s c α = 1 y ; sec\alpha=\dfrac{1}{x};\ \ csc\alpha=\dfrac{1}{y}; secα=x1; cscα=y1;
2、平方关系
s i n 2 x + c o s 2 x = 1 \begin{aligned}sin^{2}x+cos^{2}x=1\end{aligned} sin2x+cos2x=1
t a n 2 x + 1 = s e c 2 x \begin{aligned}tan^{2}x+1=sec^{2}x\end{aligned} tan2x+1=sec2x
1 + c o t 2 x = c s c 2 x \begin{aligned}1+cot^{2}x=csc^{2}x\end{aligned} 1+cot2x=csc2x
3、两角和三角函数公式
s i n ( A + B ) = s i n A c o s B + c o s A s i n B 正 余 余 正 符 号 同 ( 不 知 道 怎 么 推 导 哦 ) s i n ( A − B ) = s i n A c o s B − c o s A s i n B c o s ( A + B ) = c o s A c o s B − s i n A s i n B 余 余 正 正 符 号 异 c o s ( A − B ) = c o s A c o s B + s i n A s i n B t a n ( A + B ) = t a n A + t a n B 1 − t a n A t a n B t a n ( A − B ) = t a n A − t a n B 1 + t a n A t a n B c o t ( A − B ) = c o t A c o t B − 1 c o t B + c o t A c o t ( A − B ) = c o t A c o t B + 1 c o t B − c o t A \begin{aligned} &sin(A+B) = sinAcosB+cosAsinB \ \ \ \ \ \ \ 正余余正\ 符号同(不知道怎么推导哦)\\ &sin(A-B) = sinAcosB-cosAsinB \\ &cos(A+B) = cosAcosB-sinAsinB \ \ \ \ \ \ \ 余余正正\ 符号异\\ &cos(A-B) = cosAcosB+sinAsinB \\ &tan(A+B)=\dfrac{tanA+tanB}{1-tanAtanB} \\ &tan(A-B)=\dfrac{tanA-tanB}{1+ tanAtanB} \\ &cot(A-B)=\dfrac{cotAcotB-1}{cotB +cotA} \\ &cot(A-B)=\dfrac{cotAcotB+1}{cotB-cotA} \\ \end{aligned} sin(A+B)=sinAcosB+cosAsinB 正余余正 符号同(不知道怎么推导哦)sin(A−B)=sinAcosB−cosAsinBcos(A+B)=cosAcosB−sinAsinB 余余正正 符号异cos(A−B)=cosAcosB+sinAsinBtan(A+B)=1−tanAtanBtanA+tanBtan(A−B)=1+tanAtanBtanA−tanBcot(A−B)=cotB+cotAcotAcotB−1cot(A−B)=cotB−cotAcotAcotB+1
4、倍角三角函数公式
根据两角和公式推导哦
s i n ( 2 A ) = 2 s i n A c o s A c o s ( 2 A ) = c o s 2 A − s i n 2 A = 2 c o s 2 A − 1 = 1 − 2 s i n 2 A t a n ( 2 A ) = 2 t a n A 1 − t a n 2 A \begin{aligned} &sin(2A)=2sinAcosA \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ &cos(2A) = cos^{2}A-sin^{2}A=2cos^{2}A-1=1-2sin^{2}A \\ &tan(2A)=\dfrac{2tanA}{1-tan^{2}A} \\ \end{aligned} sin(2A)=2sinAcosA cos(2A)=cos2A−sin2A=2cos2A−1=1−2sin2Atan(2A)=1−tan2A2tanA
5、三倍角三角函数公式
s i n ( 3 A ) = 3 s i n A − 4 ( s i n A ) 3 \begin{aligned}sin(3A)=3sinA-4(sinA)^{3}\end{aligned} sin(3A)=3sinA−4(sinA)3
c o s ( 3 A ) = 4 ( c o s A ) 3 − 3 c o s A \begin{aligned}cos(3A) = 4(cosA)^{3}-3cosA\end{aligned} cos(3A)=4(cosA)3−3cosA
t a n ( 3 A ) = t a n A t a n ( π 3 + A ) t a n ( π 3 − A ) \begin{aligned}tan(3A) = tanAtan(\dfrac{\pi}{3}+A) tan(\dfrac{\pi}{3}-A)\end{aligned} tan(3A)=tanAtan(3π+A)tan(3π−A)
6、半角三角函数公式
根据倍角公式推导哦
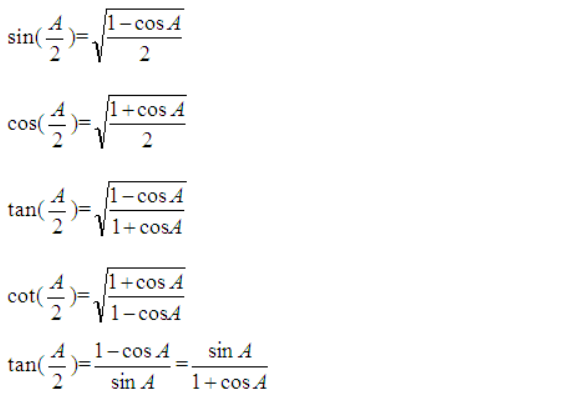
7、和差化积三角函数公式
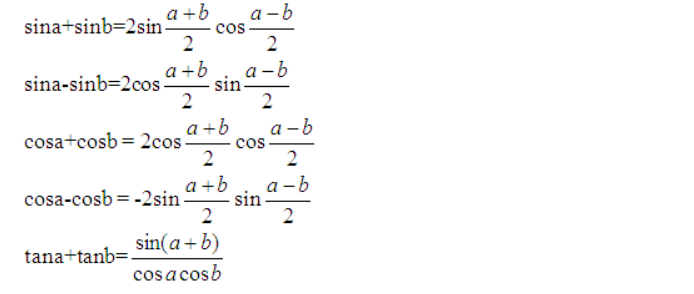
8、积化和差三角函数公式

8、诱导三角函数公式
1、适用于 s i n ( k 2 π ± α ) , c o s ( k 2 π ± α ) , t a n ( k 2 π ± α ) , c o t ( k 2 π ± α ) sin(\dfrac{k}{2}\pi \pm \alpha),cos(\dfrac{k}{2}\pi \pm \alpha),tan(\dfrac{k}{2}\pi \pm \alpha),cot(\dfrac{k}{2}\pi \pm \alpha) sin(2kπ±α),cos(2kπ±α),tan(2kπ±α),cot(2kπ±α) 的化简。
2、口诀: 奇 变 偶 不 变 , 符 号 看 象 限 。 \textcolor{red}{奇变偶不变,符号看象限。} 奇变偶不变,符号看象限。
奇偶:指 k k k 是奇数还是偶数。
\,\,\, 变: s i n ⟷ c o s , t a n ⟷ c o t sin\longleftrightarrow cos,tan\longleftrightarrow cot sin⟷cos,tan⟷cot 。
符号:把 α \alpha α 当成锐角,看 k 2 π ± α \dfrac{k}{2}\pi \pm \alpha 2kπ±α 所在象限,判断原式的正负。
s i n ( − α ) = − s i n α ; c o s ( − α ) = c o s α \begin{aligned}sin(-\alpha)=-sin\alpha;\ \ \ \ cos(-\alpha)=cos\alpha\end{aligned} sin(−α)=−sinα; cos(−α)=cosα
s i n ( π − α ) = s i n α ; c o s ( π − α ) = − c o s α \begin{aligned}sin(\pi-\alpha)=sin\alpha;\ \ \ cos(\pi-\alpha)=-cos\alpha\end{aligned} sin(π−α)=sinα; cos(π−α)=−cosα
s i n ( π + α ) = − s i n α ; c o s ( π + α ) = − c o s α \begin{aligned}sin(\pi+\alpha)=-sin\alpha;cos(\pi+\alpha)=-cos\alpha\end{aligned} sin(π+α)=−sinα;cos(π+α)=−cosα
… …