本章要解决的问题:
- 梯度到底是什么
- 梯度如何被利用到神经网络中去训练神经网络的
什么是反向传播
反向传播嘛顾名思义就是把信息反方向的传播的一种方式。在这之前我们先来看什么是正向传播, 神经网络中正向传播其实就是把信息输入神经网络, 信息通过一个一个感知机计算最后输出一个结果,说是感知器实际上就是感知机中的\(W,\,b\)对结果产生的影响。而每个\(W,\,b\)对结果产生的影响的大小就要看他们具体的数值了有的对结果影响大有的对结果影响小。
反向传播其实和正向传播是一样的,当一个神经网络没有训练好时它的结果是又偏差的,而这个偏差也是依赖于感知机中的\(W,\,b\)的数值。相对于正向传播,反向传播不只是当当反向反了而已,反的还有它的传递的信息。它传递的是偏差的信息,将这些偏差传递到一个个参数上,最后根据每个参数对偏差做出的贡献大小相应的进行修改。
反向传播是如何修改参数的
首先我们先用一个最符合直觉方法来理解一下反向传播究竟是怎么传播的,但先打个预防针,这个方法它并不正确只是可以方便我们的理解。

首先这里的\(a^{[3]}\)就是最后一层感知机输出的结果, \(\sigma\)就是激活函数啦。\(W^{[3]},\,b^{[3]}\)分别是最后一个感知机的权重和偏置,而\(a^{[2]}\)是上一层隐藏层输出的结果。 这里我们使用交叉熵来计算损失值\(J\)。

这里我们假设损失值就是个大饼,我们可以通过分配这个大饼的方式去按贡献大小分配个每个参数。在这一层中我们就可以分配个\(W^{[3]},\,b^{[3]}\)然后进行修改,但是我们并不能直接修改\(a^{[2]}\)所以我们就需要将这部分反向传播给上一层。

当然不是平均分配给每个感知机,而是需要根据每个感知机贡献的多少来进行分配,而每个感知机的参数如何调整又需要根据每个感知机的具体情况进行细分。然后我们对每个\(W^{[2]},\,b^{[2]}\)再进行调整,但它需要承担的偏差也并不是由他自己决定的还需要继续向前传播。

而前一层的感知机所需要承担的偏差是由后面所有感知机共同决定的,这里应该是需要一个算法来决定每个感知机究竟要分配多少偏差。到目前为止我们用了一个不正常但很符合直觉的办法理解反向传播是如何分配偏差的。但这种符合直觉的方法实际上在真正数值计算上并没有那么容易,那还有别的方法吗?当然有!我们前面用这种想切西瓜的方法来进行偏差的分配其实是数值的加法,那我们是否可以考虑使用向量来解决呢?使用向量的话我们就需要考虑到它不止有数值还有反向了,这就要引出梯度这个概念。
其实准确来说应该是梯度的反方向。因为按照定义梯度是指向数值增加最快的方向,而反方向就是数值减少最快的方向。
什么是梯度
\[ 梯度 = \nabla f(x,\,y) \]
这个其实就是在求\(f(x,\,y)\)这个函数的梯度。我们来看下面这张图,红色的曲面其实就是\(f(x,\, y)\)这个函数,可以看到我们可以选定曲线上任意一个点过这个点做切面,在这个切面上有无数个切线而最特殊的就是图中的黑线他表示在这条切线上函数的数值变化最快并且他与梯度密切相关。在左图中的这个向量就是梯度,他其实就是这条黑线在平面上的投影。梯度指向的方向就是函数在这个点上数值增加最快的方向,并且梯度永远都和等高线垂直。

我们现在选定一个点然后看到我们可沿着这个点做出它点梯度,因为他是个向量所以我们可以在平面中沿着坐标轴做出梯度的分量。我们假设\(x\)轴和\(y\)轴的单位向量分别是\(i,\,j\)当我们知道了单位向量后其实我们就可以把梯度的这两个分量表达出来。\(α,\,β\)分别是分量的系数,我们把分量表示出来了就可以很轻松的写出梯度的表达式了。

到这里我们实际上就是把梯度进行了分解,那么梯度他有个非常重要的意义就是它始终指向函数数值变化最快的方向。那么如果我们确定了一个点后我们想要沿着梯度的方向也就是数值变化最快的方向变化那也就变得非常简单了。

我们只需要把原来的\(x\)加上一个\(\alpha\)倍数,在原来的\(y\)上加一个\(\beta\)的倍数,而这个倍数\(\eta\)是相等的,所以就相当于梯度在\(x,\,y\)上的分量同时放大或缩小最后的方向是不变的。
如何在神经网络中使用梯度
但我们已经理解了什么事梯度后我们其实就可以把原本的损失函数\(J\)看成是前面的函数\(f\)

那么损失函数的梯度其实就是代表它增大最快的那个方向,那如果取反就是损失值减小最快的那个方向了。
以下数学不严谨,只可意会

首先这里的\(\nabla J\)就是损失函数的梯度啦,\(α, \,β, \, \gamma\) 分别是梯度在三个分量上的系数。那么根据前面讲的如果我们需要沿着梯度的反方向改变值的话我们就需要在原来的值基础上减去\(\eta\)倍的原来的系数。那么在这一层我们就可以直接对权重和偏执进行更新,但是我们并不能直接修改\(a^{[2]}\),我们需要继续进行方向传播。那既然如此我们不如对它进行一下位置的调换

我们就会发现\(β\)其实就是目前的\(a^{[2]}\)和我们期望的\(a^{[2]}\)之间的差值,而我们舍去\(\eta\)因为在之后我们继续进行反向传播它还会分配给之后的权重和偏置,所以我们不要在这里乘上这个倍数,因此我们先将他舍去以方便后续的计算。
到这里我们可以发现这里其实和损失函数有着异曲同工之妙。损失函数是表示我们期望的结果和目前的结果的差值,而这里也是表示上一层隐藏层输出的结果和我们期望的结果的差值。因此我们可以把它假设成一个“损失函数”,这里并非是真的损失函数但我们可以假设他是然后用同样的计算进行后续的操作。
上述的\(α, \,β, \, \gamma\) 并不严谨,实际上他们都是以向量的方式表达的,具体数学在这里就不细分析了,以下给出简要的表达式(不会的回去补高数!!) \[ \nabla f(x, y) \hspace{20mm}\\ =(\frac{\partial f}{\partial x},\, \frac{\partial f}{\partial y}) \hspace{10mm}\\ =\frac{\partial f}{\partial x} \cdot i + \frac{\partial y}{\partial y}\cdot j \] 这样我们就能使用偏导来代替前面的\(α, \,β, \, \gamma\) 了 \[ \alpha = \frac{\partial J}{\partial W^{[3]}} \\ \gamma = \frac{\partial J}{\partial b^{[3]}} \hspace{2mm}\\ \beta = \frac{\partial J}{\partial a^{[2]}} \hspace{1mm} \] 接下来我们就可以直接替换原本的\(α, \,β, \, \gamma\) 用偏导代替,但在下一层中的差值就不是由当当一个感知机决定了我们就前面所有的值求平均。

梯度下降法的严谨数学表达

接下来我们就用相对严谨的数学进一步的理解梯度下降法中数据是如何反向传递的。首先我们单独拎一个感知机出来看,图中的\(a^{[l-1]}\) 表示的是上一层的输出结果\(l\)表示第\(l\)层,这里的\(a^{[l-1]}\)其实是一个矩阵,矩阵的每一个值表示的是上一层每一个感知机的输出结果。\(W_i^{[l]}\)表示的是\(l\)层的所有权重每个权重都是一个向量。 \(b_i^{[l]}\)表示的是\(l\)层的偏置。我们把上一层的所有结果乘以权重矩阵的转置加上偏置就是我们的结果\(z_i^{[l]}\),但感知机的输出结果还需要通过激活函数\(\sigma\)输出结果\(a_i^{[l]}\)。虽然这样的表达已经很简洁了但是,如果我们需要一一个感知机的这么写还是很复杂。

其实我们可以直接按整层的来开这了的\(z^{[l]}\)是个矩阵代表的是\(l\)层所有的输出。权重矩阵每一行表示的是当层每一个感知机的权重,每一列其实可以看成是上一层的每一个感知机的权重。\(a^{[l-1]}\)表示的是上一层的所有输出结果,\(b^{[l]}\)表示的是\(l\)层的所有偏置。 就此我们隐藏式层算是介绍完了。接下来我们就要关注一下输出层了。
Screen Shot 2022-02-17 at 4.57.50 pm
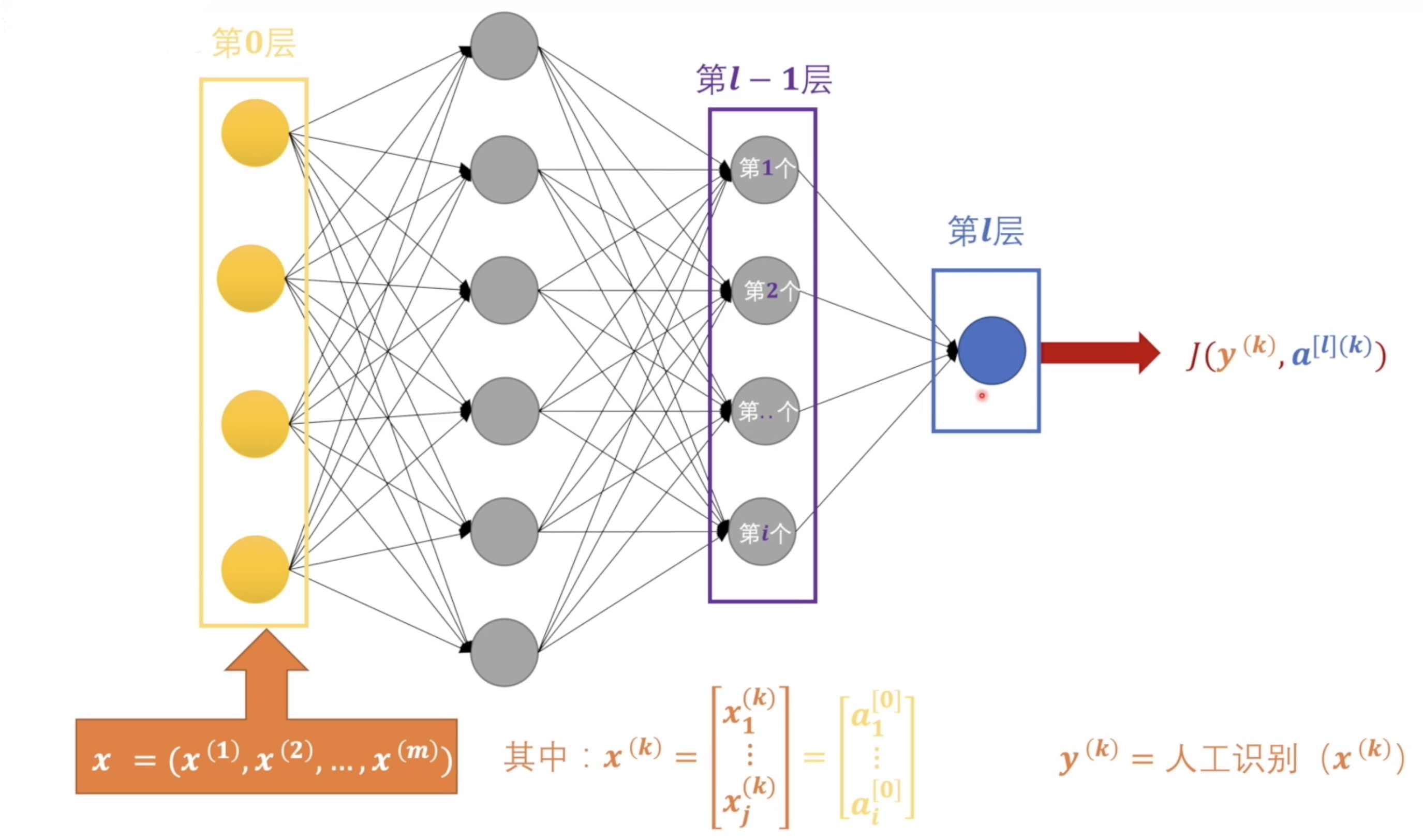
我们知道在输出层我们需要使用损失函数\(J\)来计算神经网络的输出和我们的期望的差值。这里\(a^{[l](k)}\)就是神经网络输出层输出的\(k\)个结果,\(y^{(k)}\) 其实就是我们训练数据打的标签,对于每个\(x^[(k)]\)都是人工识别标注的。在输入层中\(x\) 就是我们输入的一个一个数据,\(x^{(k)}\)的每一个值就是一个数据的分量,假设如果是图片数据那么\(x_1^{(k)} \cdots x_j^{(k)}\)就是图片的每个像素。到此为止我们考虑的都是自由一个输出结果的二分问题,实际上我们一个扩充一下 。
关于多输出的神经网络的反向传播

扩充之后输出层就不只有一个节点了而是有\(i\)个节点,每个节点都有一个输出值,而这里的损失函数\(J\)是对谁有的输出\(a_i^{[l](k)}\)的一个统一判断的损失值。也就是整体的这个神经网络离我们的预期还差多少。 因为这里我们只考虑训练神经网络的时候,在训练神经网络的时候这里的\(y^{(k)}\)和\(x^{(k)}\)都是个确定的值,不是变动参量,所以这里的损失函数我们还可以再简写一下变成\(J(a_i^{[l]})\),损失函数唯一依赖的就是神经网络最后的输出值。

我们知道如果要进行反向传播第一步就要对损失函数求梯度,那么因为损失函数依赖于最后每个感知机输出的值,所以对于每个输出都有一个分量,而这个分量就是输出层每个感知机需要承担的偏差值。为了后面描述方便我更愿意在这里添加一个虚拟的\(l+1\)层,这个\(l+1\)层不是真实存在的只是为了表述方便。我们吧每一个分量当作是一个新的误差函数,而每一个误差函数只对这一个感知机有效对别的感知机无效。

那么我们为了继续向前传播就需要对每一个误差函数求梯度,也就是这里的\(\nabla J_1^{[l+1]} \cdots \nabla J_i^{[l+1]}\)。
到这里我们就可以继续一步一步向前传播了,但为了理解我们继续展开来看看。首先我们需要关注的是\(\frac{\partial J_1^{[l+1]}}{\partial W_1^{[l]}}\),我们知道损失函数\(J\)其实是一个关于\(a^{[l]}\)的函数,而这个\(a^{[l]}\)是一个关于激活函数\(\sigma\)的函数,所以我们这里需要使用链式求导对她进行展开。 展开之后我们发现对每个分量都有一个\(\frac{\partial J_1^{[l+1]}}{\partial \sigma}\),对于这个我们就可以利用原本那个整体的损失函数\(J(a_i^{[l]})\)带进来。就会变成: \[ \nabla J_1^{[l+1]} = (\frac{ v J_1^{[l+1]}}{\partial \sigma}\frac{\partial \sigma}{\partial z_1^{[l]}}\frac{\partial z_1^{[l]}}{\partial W_1^{[l]}},\, \frac{\partial J_1^{[l+1]}}{\partial \sigma}\frac{\partial \sigma}{\partial z_1^{[l]}}\frac{\partial z_1^{[l]}}{\partial a^{[l-1]}},\, \frac{\partial J_1^{[l+1]}}{\partial \sigma}\frac{\partial \sigma}{\partial z_1^{[l]}}\frac{\partial z_1^{[l]}}{\partial b_1^{[l]}}) \] 后面为了简化表达就不继续展开了。然后我们还需要关注另一就是\(\partial W_1^{[l]}\),我们知道\(W_1^{[l]}\)是个向量所以它是有分量的,队友有分量的进行求偏导其实这里是有简化的。他其实相当于对每个分量进行求偏导。对于\(a^{[l-1]}\)也是同理。后面也不继续展开了。

但我们已经知道了这些分量后我们就可以对参数进行修改了

对于\(W,\,b\)我们就可以直接进行修改了这里的\(\eta\)其实就是我们常说的学习率了,然后对于\(a\)我们可以构建新的损失函数继续进行反向传播。这里我们利用了滑动窗口的思想来理解接下来的操作。

对于每一个损失函数求梯度,这里每一个梯度都有多个分量,每个感知机的偏差都由上一层的所有感知机共同承担。这里每一个\(a\)又都是一个关于\(W,\,a,\,b\)的函数,所以我们可以继续展开。

在这里我们需要多注意的是对于\(l\)层所有的感知机来说,他们需要承担的偏差值就不是由一个感知机来赋予的了,而是由所有的感知机共同赋予的。我们把所有偏差值的分量统一加起来求平均把它作为需要调整的的量。接下来我们就可以把所有的需要调整的偏差值写出来。 \[ (\Delta W_1^{l},\, \Delta a^{[l-1]},\, \Delta b_1^{[l]},\,\cdots\,,\,\Delta W_i^{l},\, \Delta a^{[l-1]},\, \Delta b_i^{[l]}) \]
\[ (\Delta W_1^{l},\, J_1^{[l]},\, \Delta b_1^{[l]},\,\cdots\,,\,\Delta W_i^{l},\, J_i^{[l]},\, \Delta b_i^{[l]}) \]
其中\(W,\, b\)就可以直接进行修改了,然后我们重新定义\(J_i^{[l]}\)就可以把这个循环继续下去了。
References
https://www.geogebra.org/m/HpDDHprj
https://www.bilibili.com/video/BV1Zg411T71b?spm_id_from=333.999.0.0
知识来源作者为b站UP主王木头学科学