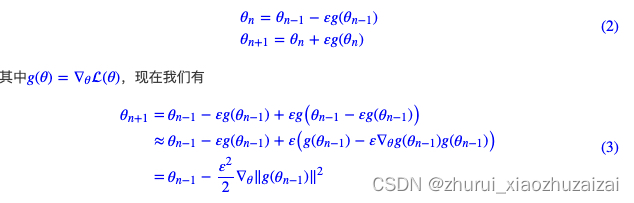输入的梯度惩罚:【对输入样本加扰动】【虚拟对抗】
参数的梯度惩罚【FLooding】
关于输入的梯度惩罚‖∇xf(x;θ)‖2
参考自:对抗训练浅谈:意义、方法和思考(附Keras实现)
对输入样本施加ϵ∇xL(x,y;θ)的对抗扰动,一定程度上等价于往loss里边加入“梯度惩罚”

梯度惩罚说“同类样本不仅要放在同一个坑内,还要放在坑底”
关于参数的梯度惩罚‖∇θf(x;θ)‖2
参考自:
我们真的需要把训练集的损失降低到零吗?
从动力学角度看优化算法(五):为什么学习率不宜过小?
过小的学习率是否可取呢?
Google最近发布在Arxiv上的论文《Implicit Gradient Regularization》试图回答了这个问题,它指出有限的学习率隐式地给优化过程带来了梯度惩罚项,而这个梯度惩罚项对于提高泛化性能是有帮助的,因此哪怕不考虑算力和时间等因素,也不应该用过小的学习率。
适当而不是过小的学习率能为优化过程带来隐式的梯度惩罚项,有助于收敛到更平稳的区域
证明过程:
离散化的迭代过程隐式地带来了梯度惩罚项,反而是对模型的泛化是有帮助的,而如果γ→0,这个隐式的惩罚则会变弱甚至消失。
因此,结论就是学习率不宜过小,较大的学习率不仅有加速收敛的好处,还有提高模型泛化能力的好处。当然,可能有些读者会想,我直接把梯度惩罚加入到loss中,是不是就可以用足够小的学习率了?理论上确实是的,原论文将梯度惩罚加入到loss中的做法,称为“显式梯度惩罚”。
在训练模型的时候,我们需要损失函数一直训练到0吗?
显然不用。正常来说训练集的损失降低到一定值后,验证集的损失就会开始上升,因此没必要把训练集的损失降低到0。
既然如此,在已经达到了某个阈值之后,我们可不可以做点别的事情来提升模型性能呢?
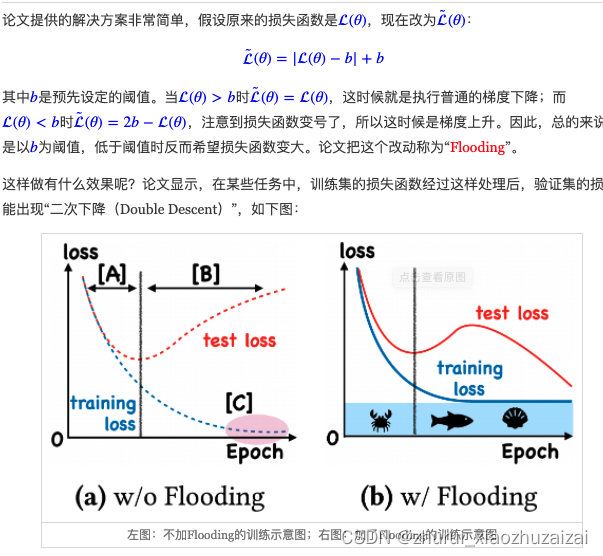
ICML 2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题。不过论文的回答也仅局限在“是什么”这个层面上,并没很好地描述“为什么”
当损失函数达到b之后,训练流程大概就是在交替执行梯度下降和梯度上升。
直观想的话,感觉一步上升一步下降,似乎刚好抵消了。事实真的如此吗?
我们来算一下看看。假设先下降一步后上升一步,学习率为ε
近似那一步是使用了泰勒展式对损失函数进行近似展开,最终的结果就是相当于损失函数为梯度惩罚‖g(θ)‖2=‖∇θ(θ)‖2、学习率为ε22的梯度下降。
更妙的是,改为“先上升再下降”,其表达式依然是一样的。
因此,平均而言,Flooding对损失函数的改动,相当于在保证了损失函数足够小之后去最小化‖∇θL(θ)‖2,也就是推动参数往更平稳的区域走,这通常能提供提高泛化性能(更好地抵抗扰动),因此一定程度上就能解释Flooding其作用的原因了。
两种梯度惩罚之间的关系:
Google最近的一篇论文《The Geometric Occam’s Razor Implicit in Deep Learning》算是部分地回答了这个问题
根据上文参数的梯度惩罚里边指出:SGD隐式地包含了对参数的梯度惩罚项,
而式(2)则说明对参数的梯度惩罚隐式地包含了对输入的梯度惩罚,而对输入的梯度惩罚又跟Dirichlet能量有关,Dirichlet能量则可以作为模型复杂度的表征。
所以总的一串推理下来,结论就是:SGD本身会倾向于选择复杂度比较小的模型。
不过,原论文在解读式(2)时,犯了一个小错误。它说初始阶段的‖W(t)‖会很接近于0,所以式(2)中括号的项会很大,因此如果要降低式(2)右边的参数梯度惩罚,那么必须要使得式(2)左边的输入梯度惩罚足够小。然而从《从几何视角来理解模型参数的初始化策略》我们知道,常用的初始化方法其实接近于正交初始化,而正交矩阵的谱范数其实为1,如果考虑激活函数,那么初始化的谱范数其实还大于1,所以初始化阶段‖W(t)‖会很接近于0是不成立的。
事实上,对于一个没有训练崩的网络,模型的参数和每一层的输入输出基本上都会保持一种稳定的状态,所以其实整个训练过程中‖h(t)‖、‖W(t)‖、‖∇xh(t)‖其实波动都不大,因此右端对参数的梯度惩罚近似等价于左端对输入的乘法惩罚。这是笔者的理解,不需要“‖W(t)‖会很接近于0”的假设。