决策树一CART算法（第四部分）

决策树一CART算法(第四部分)

---

CART树的剪枝：算法步骤

输入：CART算法生成的决策树。
输出：最优决策树T

1. 设$K=0，T=T_0$ ，从完整的决策树出发

   ​ k代表迭代次数，先从完整的树开始，即k=0开始。

2. 设$\alpha =+\infty$，后面会比较大小，损失函数小则可以剪枝，从大到小比较

3. 自下而上地对各内部结点t计其$C(T_t),|T_t|$以及
   $$g(t)=\frac{C(t)-C\left(T_t\right)}{\left|T_t\right|-1},\alpha =\min (\alpha ,g(t))$$
   $g(t)$代表了这个节点对应的$\alpha$值

   $T_t$表示以t为根结点的子树，$C(t)$ 代表单个节点的预测误差，$C(T_t)$是对训练数据的预测误差，$|T_t|$是$T_t$的叶结点个数。

   这里的预测误差与预测错误率不同，它还可以包括平方损失、基尼指数等。

4. 自上而下地访问内部结点t,如果有$g(t)=\alpha$,进行剪枝，并对叶结点t以多数表决法决定其类，得到树T。

5. 设$K=K+1,{\alpha }_k=\alpha ,T_k=T$

6. 如果T不是由根结点单独构成的树，则回到步骤(4)。

7. 采用采用交叉验证法在子树序列$T_0,T_1,T_2,...,T_n$中选取最优子树$T_{\alpha }$

损失函数

损失函数是用来度量预测错误程度的指标

原理：根据剪枝前后的 损失函数 来决定是否剪枝，剪枝后，如果损失函数减小，则意味着可以剪枝。

损失函数：
$$C_{\alpha }=C(T)+\alpha |T|$$
$C_{(}T)$反映代价，是对训练数据的预测误差（比如基尼指数），代表模型的[拟合能力]。

$\alpha$是一个决定拟合和泛化综合效果的参数，$\alpha$反映了复杂度的程度，如果越大，说明复杂度更重要，如果为零，则只与预测误差有关

$|T|$反映的是模型的复杂度，体现 [泛化能力]， $|T|$表示子树上叶子结点的个数，叶子结点越多，模型越复杂。

当α=0时，模型仅由拟合决定，没有对未知数据的预测能力，得到一棵最完整的决策树，泛化能力弱。
当$\alpha =+\infty$时，得到的是单结点树，对于任何数据的泛化能力很强，但拟合效果差。

$\alpha$ 的取值

将$\alpha$从 0到 $+\infty$划分成多个小区间。比如：
$$0\le {\alpha }_0<{\alpha }_1<{\alpha }_2<{\alpha }_3....<{\alpha }_n<{\alpha }_{n+1}<+\infty$$
每一个$\alpha$ 就对应着一棵决策树。划成小区间:
$$[{\alpha }_1,{\alpha }_2),[{\alpha }_2,{\alpha }_3),....[{\alpha }_n,{\alpha }_n+1),$$
总共有$n$个区间，每个小区间都对应着一个决策树，我们可以记成：
$$T0,T_1,T_2,T_3....T_n$$
现在要找到最优的决策树。现在我们有一棵子树$T_t$。

剪枝前的损失函数写成：
$$C_{\alpha }\left(T_t\right)=C\left(T_t\right)+\alpha \left|T_t\right|$$
剪枝后变成了一个叶子结点，损失函数可以写成：
$$C_{\alpha }\left(T_t\right)=C(t)+\alpha$$
假设$\alpha$ 从 0开始逐渐变大到 $+\infty$，变化趋势为高度拟合到高度泛化，得出在高度拟合和高度泛化时，所对应的损失函数都是非常大的。

而在这变化过程中，剪枝前和剪枝后的会有一个临界值 ，在这个临界值处，[拟合] 和 [泛化] 的损失函数为最小。

联立两个方程求解：
$$\begin{gathered} C(t)+\alpha =C\left(T_t\right)+\alpha \left|T_t\right| \\ \alpha =\frac{C(t)-C\left(T_t\right)}{\left|T_t\right|-1} \end{gathered}$$

---

CART算法剪枝例题

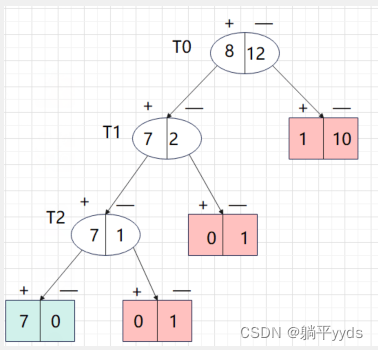
按照刚开始的算法步骤：

第一轮判断剪枝：

1. **设$K=0，T=T_0$ **

2. 设$\alpha =\infty$ ,图中有3个内部结点，分别是$T_0、T_1、T_2$记为t=0，t=1，t=2，对应的叶子结点有4个。绿色 表示正类，红色表示负类

3. 计算:

   自下而上地对各内部结点t计其$C(T_t),|T_t|$以及
   $$g(t)=\frac{C(t)-C\left(T_t\right)}{\left|T_t\right|-1},\alpha =\min (\alpha ,g(t))$$
   $g(t)$代表了这个节点对应的$\alpha $值

   $T_t$表示以t为根结点的子树，$C(t)$ 代表单个节点的预测误差，$C(T_t)$是对训练数据的预测误差，$|T_t|$是$T_t$的叶结点个数。选用的是预测错误率来计算。

   $T_0子树$ ：

   ​ 样本总数为20个，8个负类，12个负类，权重为：子树中的样本点占总体的个数。按照多数表决法来设置单结点的话，那么应该设为负类
   $$C_0=\frac{20}{20}\times \frac{8}{20}=\frac{8}{20}$$
   $C(T0)$中只有一个误判，因此$C(T_0)=\frac{1}{20}$

   带入计算：
   $$g(0)=\frac{C(0)-C\left(T_0\right)}{\left|T_0\right|-1}=\frac{\frac{8}{20}-\frac{1}{20}}{4-1}=\frac{7}{60}$$
   取：
   $$\alpha =\min (\alpha ,g(0))=\min (+\infty ,\frac{7}{60})=\frac{7}{60}$$
   $T_1子树$ ：

   ​ 样本总数为9个，7个正类，2个负类，权重为：子树中的样本点占总体的个数。按照多数表决法来设置单结点的话，那么应该设为正类
   $$C_0=\frac{9}{20}\times \frac{2}{9}=\frac{1}{10}$$
   $C(T_1)$中没有误判，因此$C(T_1)=0$

   带入计算：
   $$g(1)=\frac{C(0)-C\left(T_0\right)}{\left|T_0\right|-1}=\frac{\frac{1}{10}-0}{3-1}=\frac{1}{20}$$
   取：
   $$\alpha =\min (\alpha ,g(1))=\min (\frac{7}{60},\frac{1}{20})=\frac{1}{20}$$

   $T_3子树$：

   ​ 样本总数为8个，7个正类，2个负类，权重为：子树中的样本点占总体的个数。按照多数表决法来设置单结点的话，那么应该设为正类
   $$C_0=\frac{8}{20}\times \frac{1}{8}=\frac{1}{20}$$
   $C(T0)$中只有一个误判，因此$C(T_0)=0$

   带入计算：
   $$g(2)=\frac{C(0)-C\left(T_0\right)}{\left|T_0\right|-1}=\frac{\frac{2}{20}-0}{2-1}=\frac{1}{20}$$
   取：
   $$\alpha =\min (\alpha ,g(2))=\min (\frac{1}{20},\frac{1}{20})=\frac{1}{20}$$
   由于$g(1)=g(2)=\frac{1}{20}$,因此可以对内部节点$T_2$子树剪枝
   

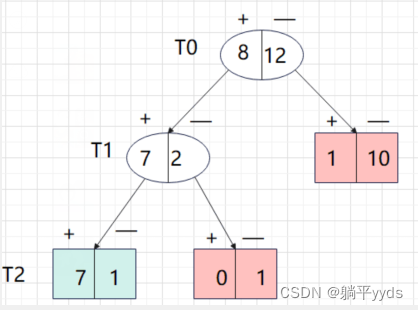
第二轮判断剪枝：

​ 按照上面的思路对$T_0和T_1$内部几点进行迭代运算

$T_0子树$ ：

​ 样本总数为20个，8个负类，12个负类，权重为：子树中的样本点占总体的个数。按照多数表决法来设置单结点的话，那么应该设为负类
$$C_0=\frac{20}{20}\times \frac{8}{20}=\frac{8}{20}$$
剪枝之后，$C(T_0)$对应的3个叶子节点钟误判个数为2个，因此$C(T_0)=\frac{2}{20}$

带入计算：
$$g(0)=\frac{C(0)-C\left(T_0\right)}{\left|T_0\right|-1}=\frac{\frac{8}{20}-\frac{2}{20}}{3-1}=\frac{3}{20}$$
取： 这里的比较的$\alpha$是第一轮中的结果，也就是$\frac{1}{20}$
$$\alpha =\min (\alpha ,g(0))=\min (\frac{1}{20},\frac{3}{20})=\frac{1}{20}$$
$T_1子树$ ：

​ 样本总数为9个，7个正类，2个负类，权重为：子树中的样本点占总体的个数。按照多数表决法来设置单结点的话，那么应该设为正类
$$C_0=\frac{9}{20}\times \frac{2}{9}=\frac{1}{10}$$
$C(T_1)$子树中2个节点误判了一个，因此$C(T_1)=\frac{1}{20}$

带入计算：
$$g(1)=\frac{C(0)-C\left(T_0\right)}{\left|T_0\right|-1}=\frac{\frac{2}{20}-\frac{1}{20}}{2-1}=\frac{1}{20}$$
取：
$$\alpha =\min (\alpha ,g(1))=\min (\frac{1}{20},\frac{1}{20})=\frac{1}{20}$$
​ 可以看出$T_1$子树对应$\alpha$是最小值，意味着对$T_1$剪枝

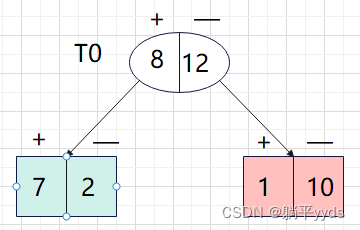
第三轮判断剪枝：

​ 按照上面的思路对$T_0$节点进行迭代运算

$T_0子树$ ：

​ 样本总数为20个，8个负类，12个负类，权重为：子树中的样本点占总体的个数。按照多数表决法来设置单结点的话，那么应该设为负类
$$C_0=\frac{20}{20}\times \frac{8}{20}=\frac{8}{20}$$
剪枝之后，$C(T_0)$对应的2个叶子节点钟误判个数为3个，因此$C(T_0)=\frac{3}{20}$

带入计算：
$$g(0)=\frac{C(0)-C\left(T_0\right)}{\left|T_0\right|-1}=\frac{\frac{8}{20}-\frac{3}{20}}{2-1}=\frac{5}{20}$$
取： 这里的比较的$\alpha$是第二轮中的结果，也就是$\frac{1}{20}$
$$\alpha =\min (\alpha ,g(0))=\min (\frac{1}{20},\frac{5}{20})=\frac{1}{20}$$
由结果可知，$T_0$子树对应的不是最小的$\alpha$，所以不剪枝。同时，根节点满足了两个叶子结点的停止条件，[剪枝结束]。

总结：对于树形结构比较复杂的决策树而言，可以继续增加迭代次数，最终采用交叉验证法将原始的决策树和每轮生成的Tree1、Tree2…等决策树中选取最优树形