机器学习基础自学笔记——k邻近算法

k邻近算法，英文全称K Nearest Neighbors，简称KNN

概念引入

k邻近算法的基础原理其实十分简单。我们来看下面一个例子：

​ 在橙色和浅黄绿色圆中间有一个小黑点。现在小黑点跟你说，它也想要靠边站，但是它不知道是跟橙色圆还是浅黄绿色圆，让你帮忙。相信你第一反应就是看小黑点跟谁近，跟谁近就属于谁。经过测量，发现小黑点与橙色圆的距离为a，与浅黄绿色圆的距离为b，而且$a>b$。相信这时候你就知道小黑点应该属于谁了。这就是k邻近算法的基础原理，上图也是最简单的情况之一。

​ 不过这时候，橙色圆不乐意了。凭什么小黑点归浅黄绿色？凭什么离得近就属于谁？于是他叫来了很多自己的兄弟。于是呈现出了下图的情况。

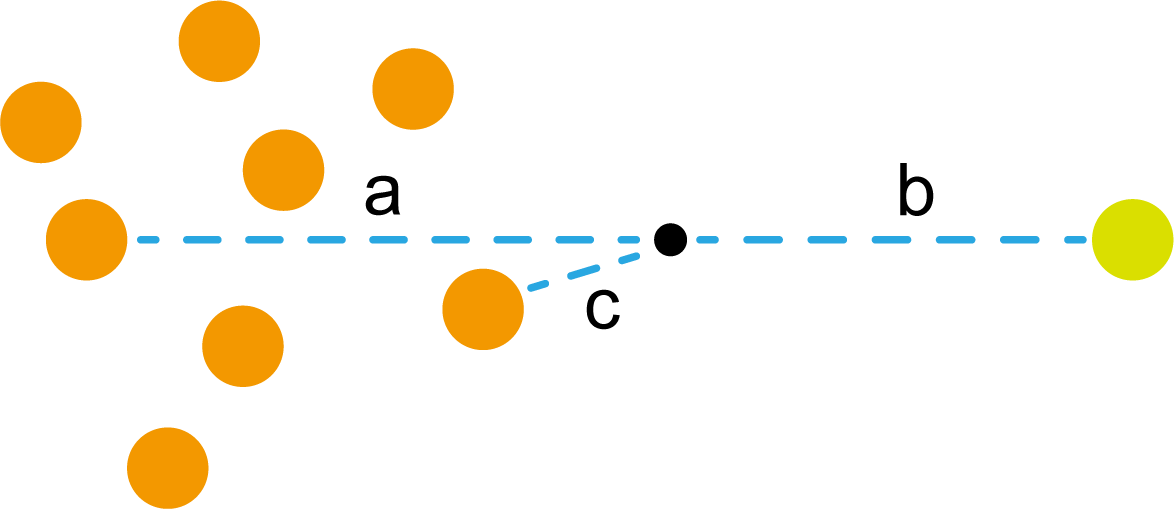
​ 这时候橙色圆距离小黑点最近的距离变成了c，而且$c<b$。这时候橙色圆说，小黑点应该归我们！浅黄绿色圆也不干了，它觉得应该算小黑点到所有圆距离的平均值，然后比较平均值大小。但是无奈橙色圆人多势众啊，于是浅黄绿色圆也叫来了自己的弟兄们。

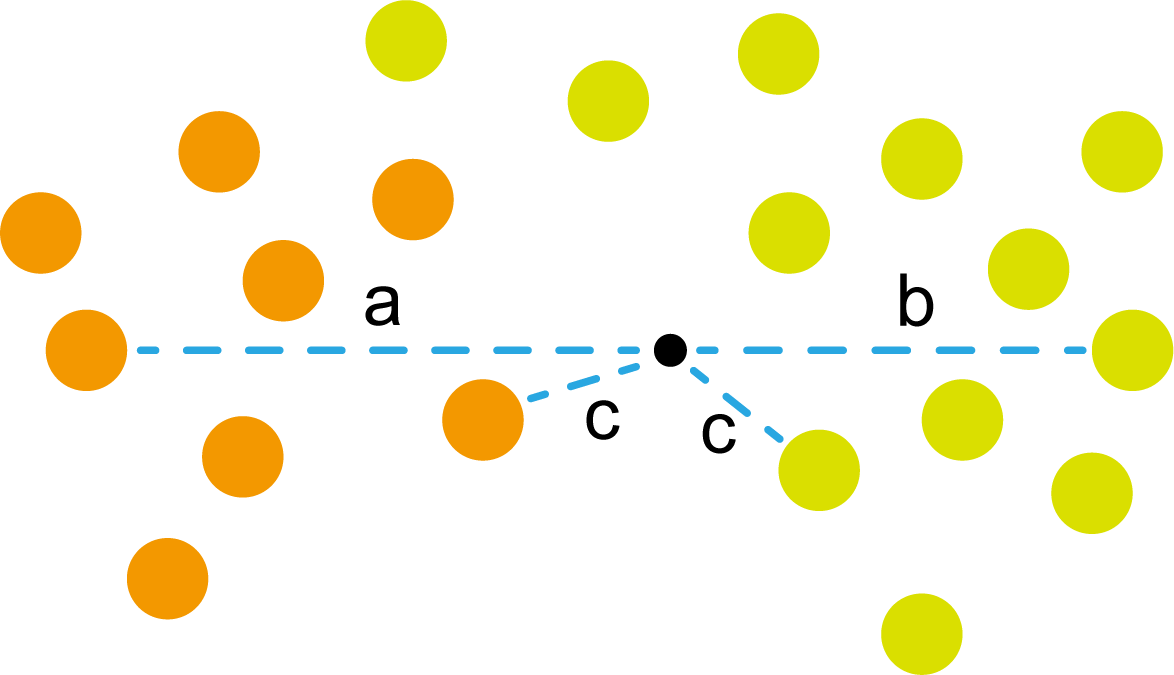
这些浅黄绿色圆更过分，直接跑到橙色圆跟前挑衅。经过测量，发现此时的小黑点到橙色圆和浅黄绿色圆的最近距离都是c。这下吵得不可开交了。火上浇油的时候，这时候紫色圆也跑了过来，也要抢小黑点。

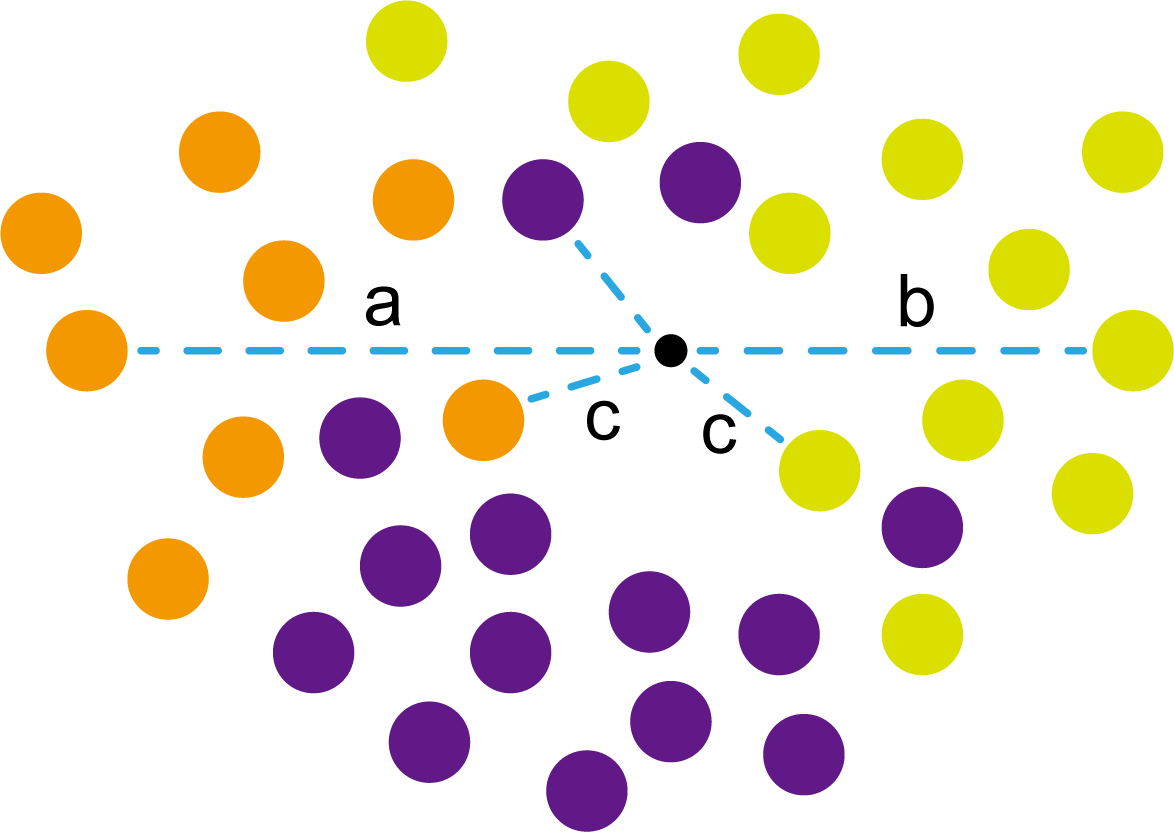
那么这时候应该将小黑点归属于谁呢？

这是个好问题。

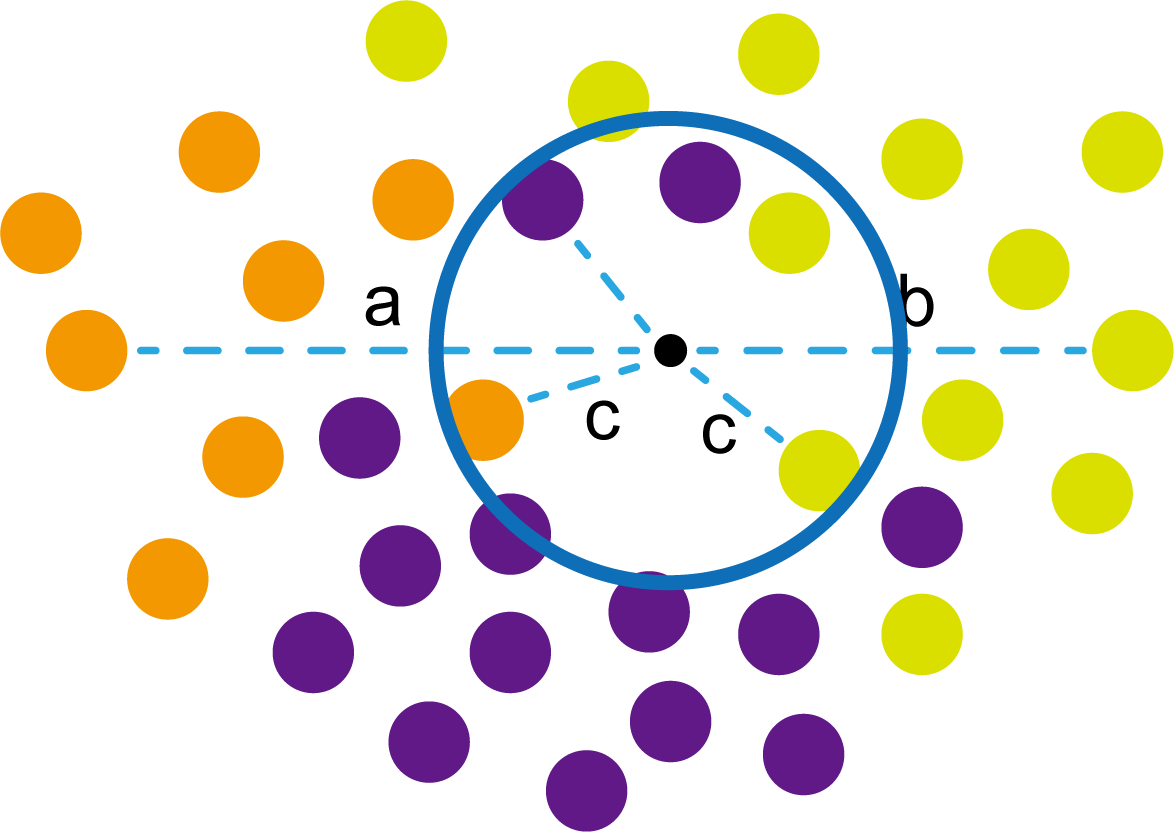
这里的评判标准有很多，而对于KNN算法来说，它的方法是在小黑点周围画一个圈，然后观察圈里哪个圆形的数量比较多，小黑点就属于谁。

我们采取四舍五入的方法，把在蓝色圈内的大于圆面积一半的圆算在园内，我们统计下三种颜色的圆各有多少个：

• 橙色：2个

• 浅黄绿色：6个

• 紫色：9个

这个统计的过程就是一个投票的过程。而这个投票由少数服从多数，所以在该情况下，小黑点应该属于紫色圆。在蓝色大圆中总共有17个小圆，所以k=17（一般实际情况下k不会取到17这么大）

但是KNN算法也会有失效的时候，比如下种情况：

在蓝色圈内的紫色圆数量和浅黄绿色圆的数量相同，这时候就无法判断出小黑点的归属。

相比于别的监督学习方法，KNN算法可以算作是极其简单的了。

KNN算法特点

（1）惰性。惰性的意思是不需要先对数据进行大量训练，只需要把已分类好的数据放在那就行。但是像线性回归算法等，都需要预先训练好权重参数等，才能放入进行归类或者预测。

KNN算法实现步骤

1）拥有类别的样本

就像第一个例子中的那些各种颜色的圆。如果没有那些各种颜色（一种颜色就是一种类别）的圆，那么就无从去判断“小黑点”究竟属于哪一类

2）选取测量距离的方式，测算未知类别的样本与所有已知类别的样本的距离

或许会有人觉得奇怪，测量距离的方式不就是两个点的最短路径吗还有别的方式吗？事实上，这里的距离应该指的是广义距离。下面我来介绍一下几种距离的方式。

① 欧式距离

欧式距离就是我们最常见的距离度量方法，就是两点之间的最短距离。

假设两个点的坐标分别为$x_1(x_{11}，x_{12}，x_{13}，\cdot \cdot \cdot ，x_{1n})$，$x_2(x_{21}，x_{22}，x_{23}，\cdot \cdot \cdot ，x_{2n})$，（我们也称$x_{11}，x_{12}，x_{13}，\cdot \cdot \cdot ，x_{1n}$为$x_1$的特征）则这两个点的欧式距离为：
$$L(x_1,x_2)=\sqrt{\sum _{i=1}^n(x_{1i}-x_{2i}{)}^2}$$
② 曼哈顿距离

假设两个点的坐标分别为$x_1(x_{11}，x_{12}，x_{13}，\cdot \cdot \cdot ，x_{1n})$，$x_2(x_{21}，x_{22}，x_{23}，\cdot \cdot \cdot ，x_{2n})$，则这两个点的曼哈顿距离为：
$$L(x_1,x_2)=\sum _{i=1}^n|x_{1i}-x_{2i}|$$
③ 切比雪夫距离

假设两个点的坐标分别为$x_1(x_{11}，x_{12}，x_{13}，\cdot \cdot \cdot ，x_{1n})$，$x_2(x_{21}，x_{22}，x_{23}，\cdot \cdot \cdot ，x_{2n})$，则这两个点的切比雪夫距离为：
$$L(x_1,x_2)=(\sum _{i=1}^n|x_{1i}-x_{2i}{|}^p{)}^{\frac{1}{p}}$$
其中p趋于正无穷。

其实，上面三种计算方法可以进行一个统一。欧氏距离是$L(x_1,x_2)=({\sum }_{i=1}^n|x_{1i}-x_{2i}{|}^p{)}^{\frac{1}{p}}$中$p=2$的结果，曼哈顿距离是该式$p=1$的结果，而切比雪夫距离是$p=+\infty$的结果

3）从中选取与未知类别样本距离最近的k个已知样本

如何选取k的值是一个学问。如果k值选取的太大容易造成欠拟合，如果k值选取的太小容造成过拟合

• 如果我们假设k为1（即为最近邻算法），此时的错误率（误分类可能性）比较高，因为很容易受到极个别特殊情况影响（如下图）。

上图中距离小黑点最近的是一个浅黄绿色的圆，但是很明显可以看出来，这个圆距离其它浅黄绿色圆比较远，是一种极端情况，所以其实这个小黑点大概率应该划给橙色圆

• 如果我们假设k为N，即根据所有点来判断，此时就是哪个圆数量多就归属于哪个圆，这显然也是不合理的，下图就是一个反例：

• 而当k值取在1和N中间的时候，随着k的变大，错误率会先下降后上升，会有一个极小值点作为最适合的k值。k到底取什么值，没有一个现成的算法可以告诉你，但是我们可以通过一些技巧和理解来缩小k值所取的范围。
  • k一般取奇数（尤其是只有两种分类），这样可以避免两个类别占比相等的情况
  • 一般k值都比较小，可以这么想：k值越大，说明需要考虑的距离小黑点更远的圆更多。而离小黑点较远的圆其实对小黑点的影响并不是很大，所以看k值不宜过大。

4）根据少数服从多数，进行“投票”

就是比较各类别的数目大小

5）确定未知分类样本归类为哪一类

KNN算法关键

（1）样本的所有特征都要做可比较的量化。

比如样本中存在非数值类型，则需要想办法将其转化为数值。例如样本中如果有颜色，则需要将颜色转化成灰度值进行比较。

（2）样本特征要做归一化处理

样本有多个参数，每一个参数都有自己的定义域和取值范围，为了“公平竞争”，所有特征的数值都采取归一化处置。

如下图：

左图中的圆大小不一，就像每一个参数都有自己的定义域和取值范围，而为了避免这种影响需要进行统一，统一成右图。

（3）需要一个距离函数以计算两个样本之间的距离

通常使用的距离函数有：欧氏距离、余弦距离、汉明距离、曼哈顿距离等，一般选欧氏距离作为距离度量，但是这是只适用于连续变量。在文本分类这种非连续变量情况下，汉明距离可以用来作为度量。不同的度量方法适用于不同的样本。

KNN算法的优缺点

KNN算法的优点：

（1）简单，易于理解，易于实现，无需估计参数，无需训练；

这个很好理解，我在之前也介绍过，这称之为“惰性”

（2）适合对稀有事件进行分类；

（3）特别适合于多分类问题(multi-modal,对象具有多个类别标签)

KNN算法的缺点：

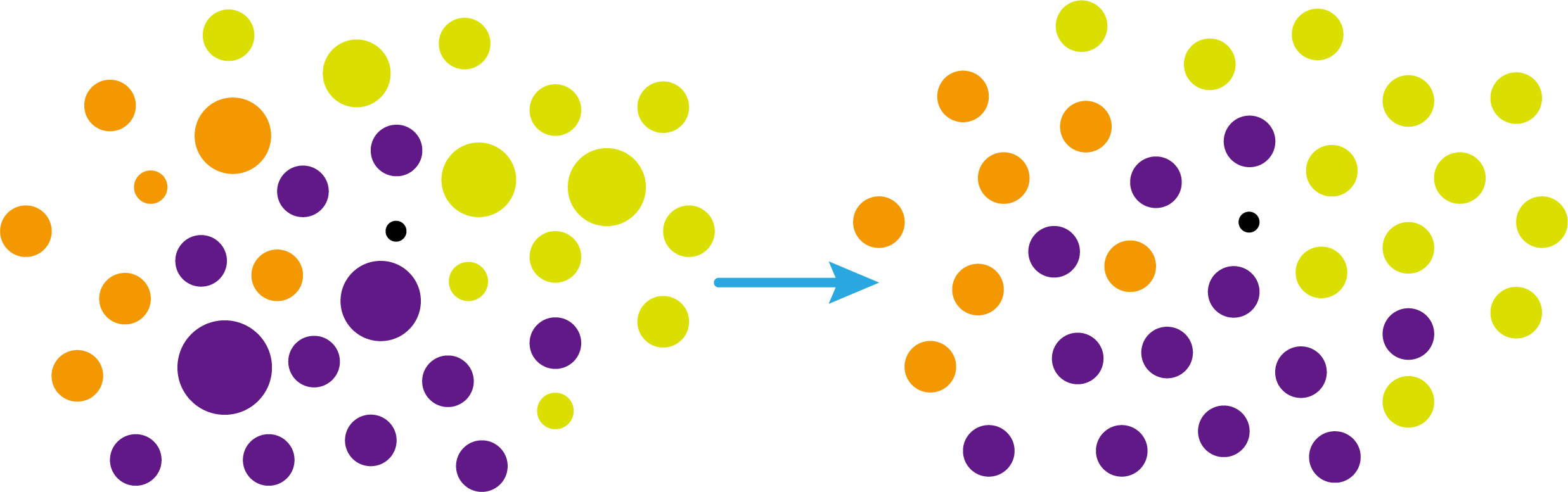
​ KNN算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数，如下图所示。

在该图中，虽然直观感觉小黑点应该属于橙色圆，但是如果画一个如上图的蓝色圈，蓝色大圈内的浅黄绿色圆的数量要多于橙色圆的数量。

改进方法：
可以采用权值的方法(该样本距离小的邻居权值大)来改进。

KNN算法优化——kd树

​ 前面说到，KNN算法需要测量待分类点(小黑点)和每一个已分类点（各种颜色的圆）的距离，并进行排序，选出其中k个距离最近的圆，再进行投票。这个算法在理解上十分简单，但是，如果当数据集十分大的时候，比如有100万个数据点，此时每个数据点还有几十个特征，那么计算起来将会十分复杂。那么有没有一种方式可以减少这样的计算量呢？

答案是肯定的。

这时候，人们结合数据结构中的二叉树，提出了一种算法——kd树（k-dimensional tree）

kd树可以帮助我们很快地找到与测试点最相邻的k个训练点，而不需要计算每个待分类点与已知分类点的距离。为了方便理解，我们还是举一个例子来说明。

kd树的构造

例子引入

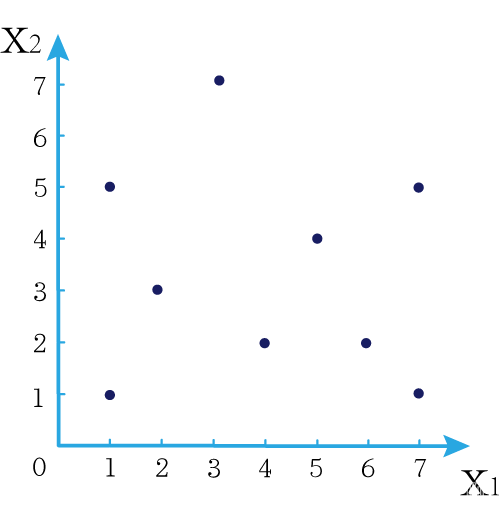
现在我们有以下二维数据点：$(1,1),(1,5),(2,3),(3,7),(4,2),(5,4),(6,2),(7,1),(7,5)$，我们要利用这些数据点构造一棵kd树。

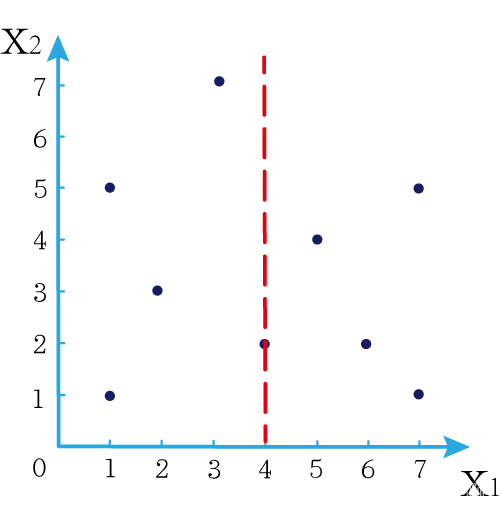
第一步我们根据所有点的$x_1$找到中位数，上图中对应的中位数是4，所以该中位数对应的那个点是$(4,2)$。我们经过$(4,2)$画一条垂直于$x_1$轴的竖线，那么此时这条竖线（红色虚线）将所有数据点分成左右两个部分。

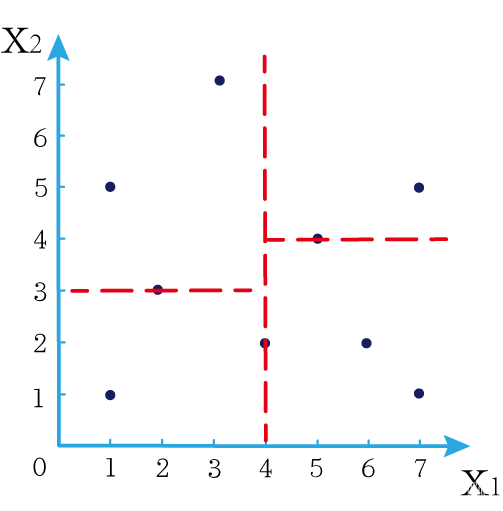
下面我们分别对左右的数据点重复上述操作，但是需要注意的是，此时是根据所有点的$x_2$来计算中位数，所画的线应该垂直于$x_2$轴。

注意对于这个情况来说，左边四个点无法找到中位数，此时我们只要选取处于中间两个数的任意一点即可

按上述操作继续划分，直到分割的小区域内只剩下一个点或者没有点。

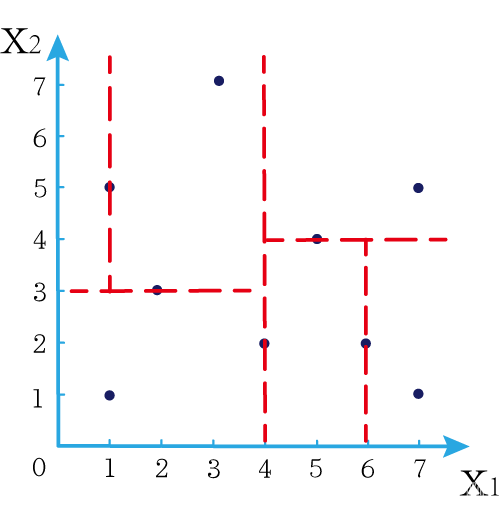
这样我们就完成了一个kd树的划分。

那为什么说这是一颗“树”呢？

实际上，随着我们的划分过程，我们会不断的构造一棵二叉树。我们先经过$(4,2)$划了一条竖线，那么我们将$(4,2)$纳入根结点。之后我们划竖线经过了$(2,3)$$(5,4)$这两个点，那我们将其分别作为左结点和右结点.

注意：左结点和右结点的划分是有条件的。

对于$(4,2)$来说，我们是根据$x_1$的值划分了数据点，那么左结点$x_1$坐标比根结点小，比如2<4；右结点$x_1$坐标比根结点大，比如$5>4$。而对于$(2,3)$来说，由于我们是根据$x_2$轴划分的数据点，那么左结点$x_2$坐标比根结点小，右结点$x_2$坐标比根结点大。

以此类推。如果没有划竖线，那么我们就将其作为空结点。所以我们能得到一个如下图的二叉树。

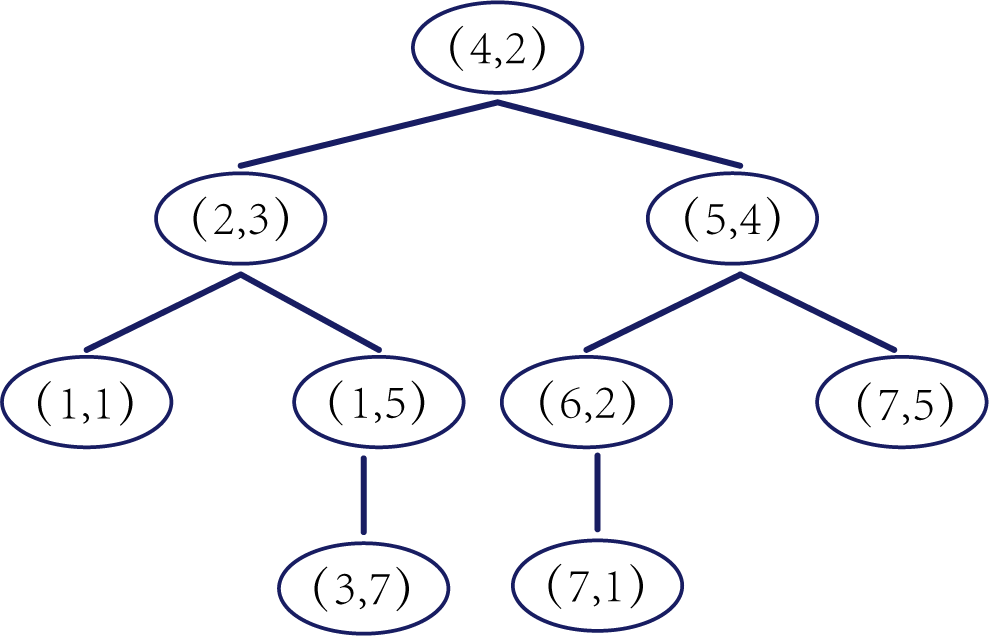
下面我们就需要利用kd树完成k近邻搜索。假设现在我们有一个点$(3,4)$，我们要去寻找这个点的最近邻点。

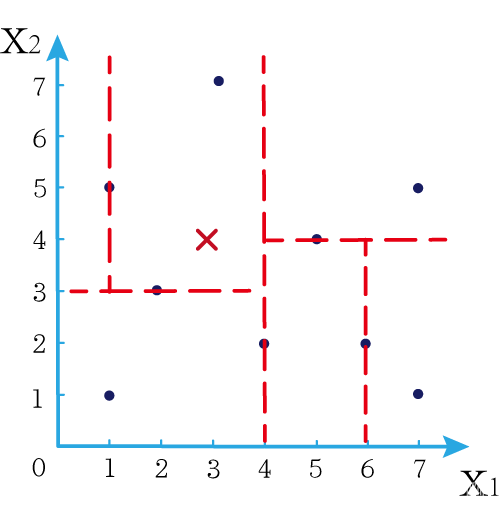
寻找最近邻点的过程其实是一个搜寻二叉树的过程。我们还可以在坐标轴上进行直观的理解。

为了方便，我将所有点依次命名为A~E，将待分类的点命名为p，将k近邻点存放在S中，S功能存放k个数据点（我们这里设k=3）。

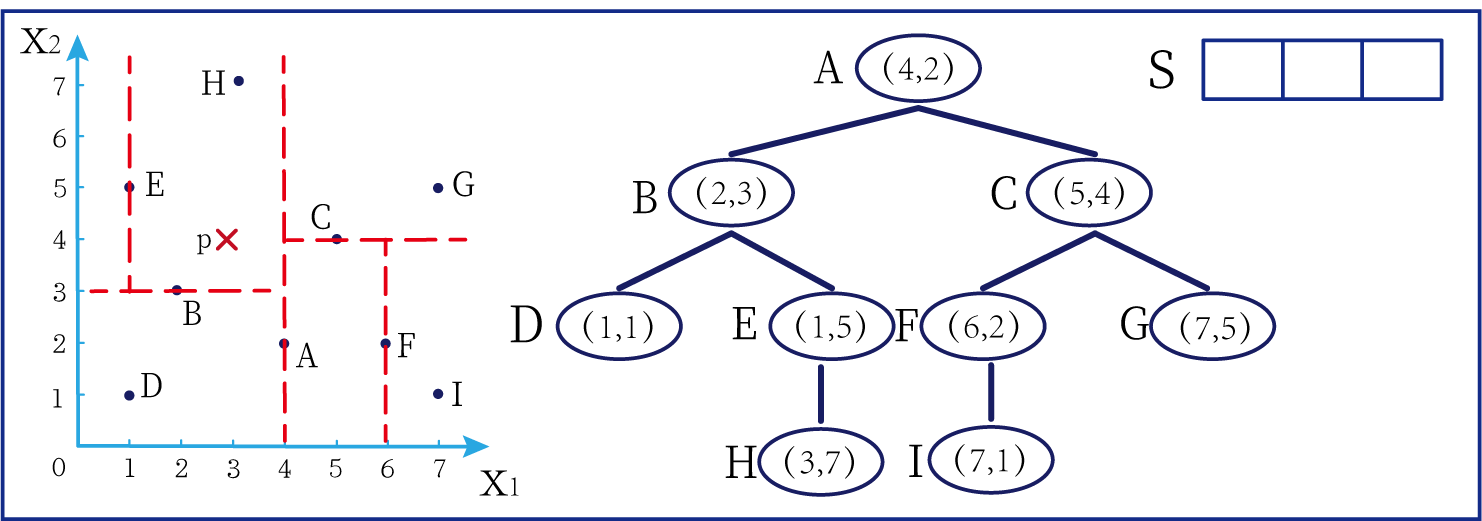
算法描述

1. 选取$x_1$为坐标轴，以训练集中的所有数据$x_1$坐标中的中位数作为切分点，将超矩形区域切割成两个子区域。将该切分点作为根结点，由根结点生出深度为1的左右子结点，左节点对应$x_1$坐标小于切分点，右结点对应坐标大于切分点
2. 对深度为j的结点，选择$x_i$为切分坐标轴，其中$i=j(modk)+1$，以该结点区域中训练数据$x_i$坐标的中位数作为切分点，将区域分为两个子区域，且生成深度为j+1的左、右子结点。左节点对应$x_i$坐标小于切分点，右结点对应$x_i$坐标大于切分点
3. 重复2，直到两个子区域没有数据或者只有一个数据时停止。

kd树的搜索

例子引入

下面开始kd树搜索。

• 第一步：
• 首先我们将$(3,4)$与根结点$(4,2)$进行比较。由于之前是垂直于$x_1$的轴经过$(4,2)$，所以去比较两个点的$x_1$坐标。由于$3<4$，所以我们往根结点的左结点进行搜寻（因为我们在之前构造kd树的时候规定了左结点小而右结点大）。

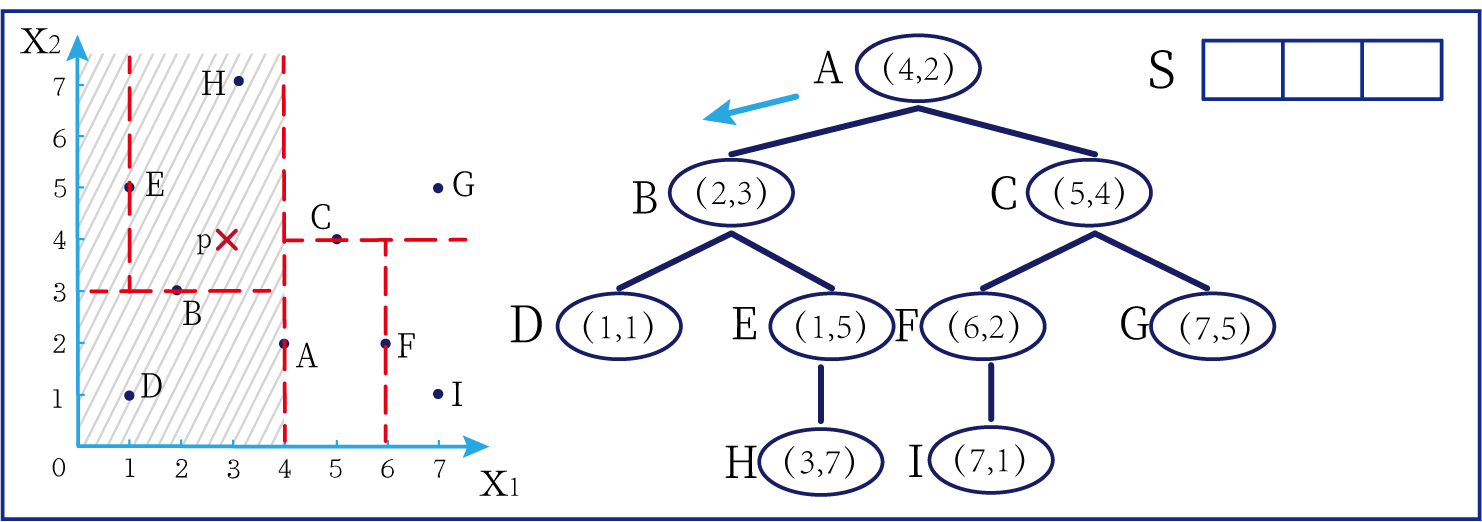
在上图中左边坐标轴中对应的是左边阴影部分的区域，接下来的搜索要在阴影部分进行

• 第二步：
• 接下来需要将$(3,4)$的$x_2$与左子树的根结点$(2,3)$的$x_2$坐标进行比较，由于$4>3$，所以要往右搜索

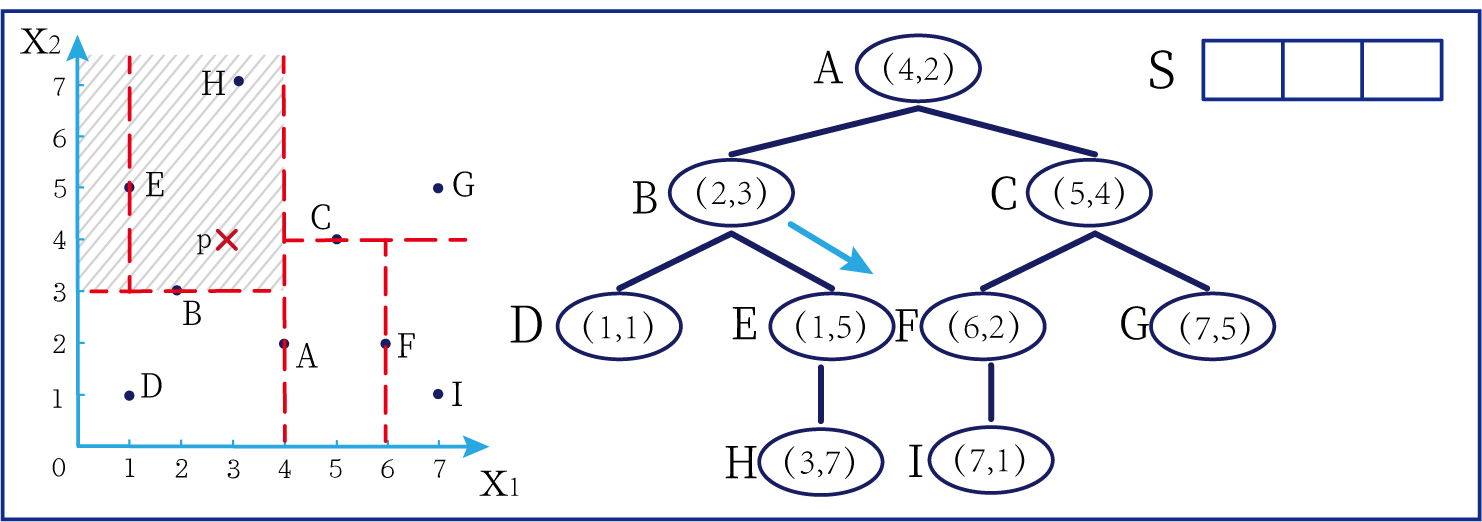
在上图中左边坐标轴中对应的是左上角阴影部分的区域，接下来的搜索要在阴影部分进行。

• 第三步：
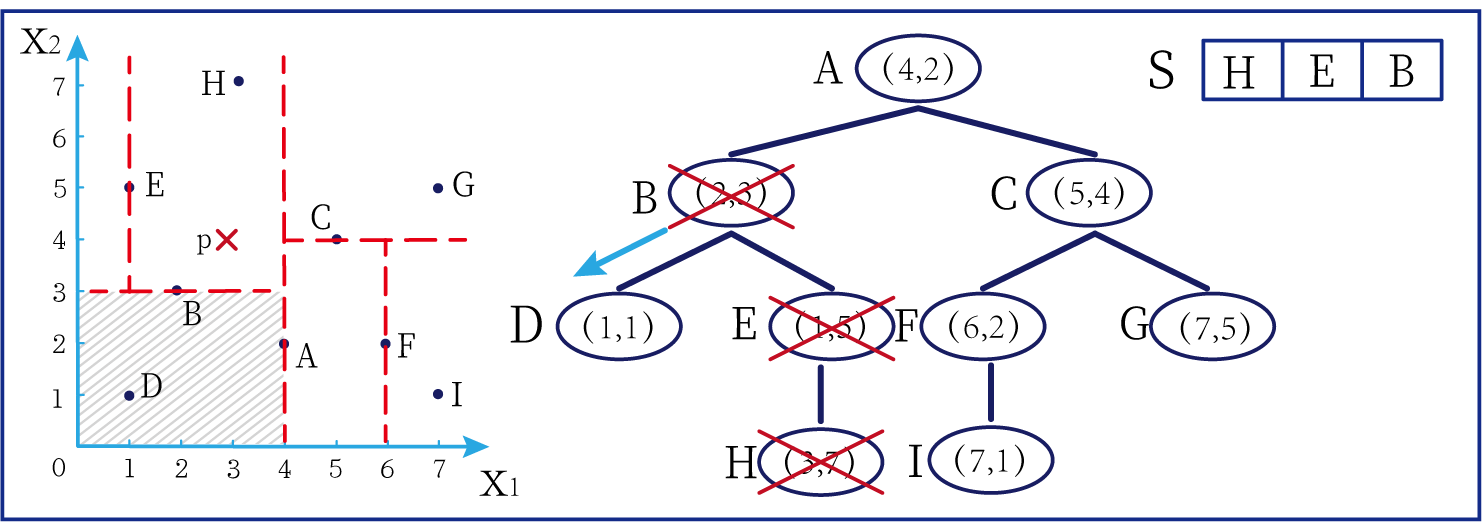
• 由于E结点只有一个子结点，所以经过E结点时无需比较坐标大小可以直接搜索到H结点。由于H点是叶子结点，接下来无法继续这个分支的遍历，所以我们标记一下H结点，说明我们已经访问过这里且不需要再次进行访问。此时我们发现，S里是空的，我们可以暂且将H点存入S中，作为一个k邻近点（但是不代表这个点就是邻近点，后续会进行替换操作）

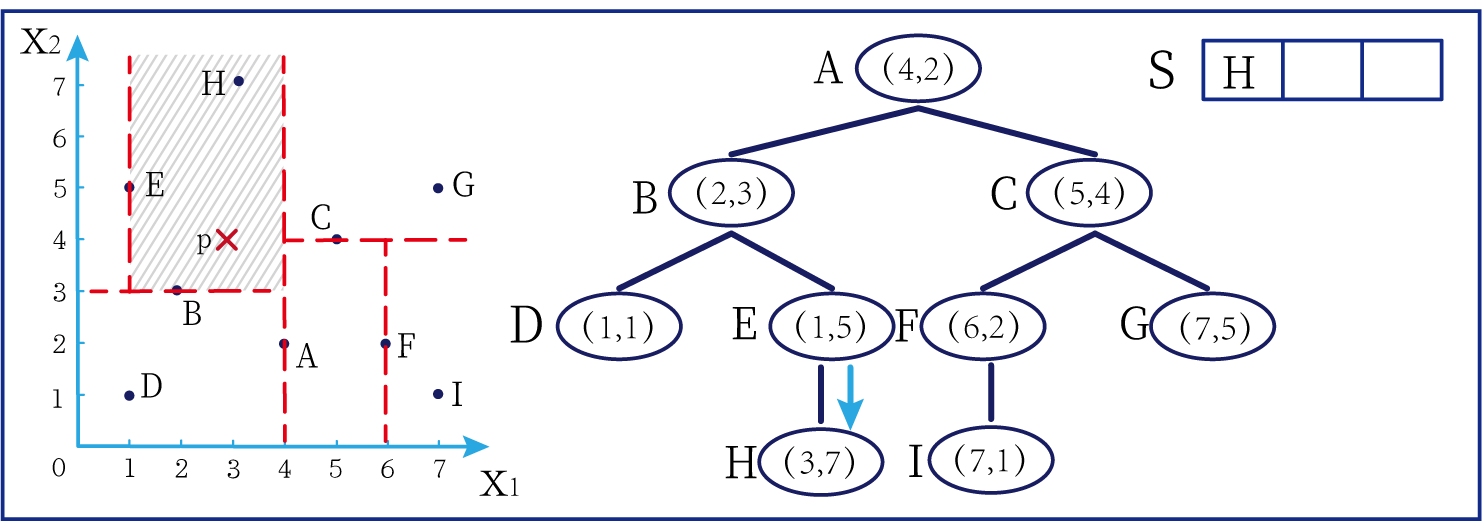
在上图中左边坐标轴中对应的是左上角阴影部分的区域，接下来的搜索要在阴影部分进行。此外，S中存入了H结点

• 第四步：
• 由于H点是叶结点，无法继续进行访问，所以要退回上一个结点C。因为C只有一个分支，所以这条分支已经搜索过了，我们便可以标记一下结点E，并将E结点存入S中。

在上图中左边坐标轴中对应的是左上角阴影部分的区域，阴影区域扩大，说明接下来要扩大搜索范围搜索尚未搜索过的区域。此外，S中存入了E结点；H结点从kd树上划去，之后不再进行搜索。

• 第五步：
• 由于E结点没有别的分支了，所以继续退回到上一个结点B。将结点B进行标记，并加入到S中。

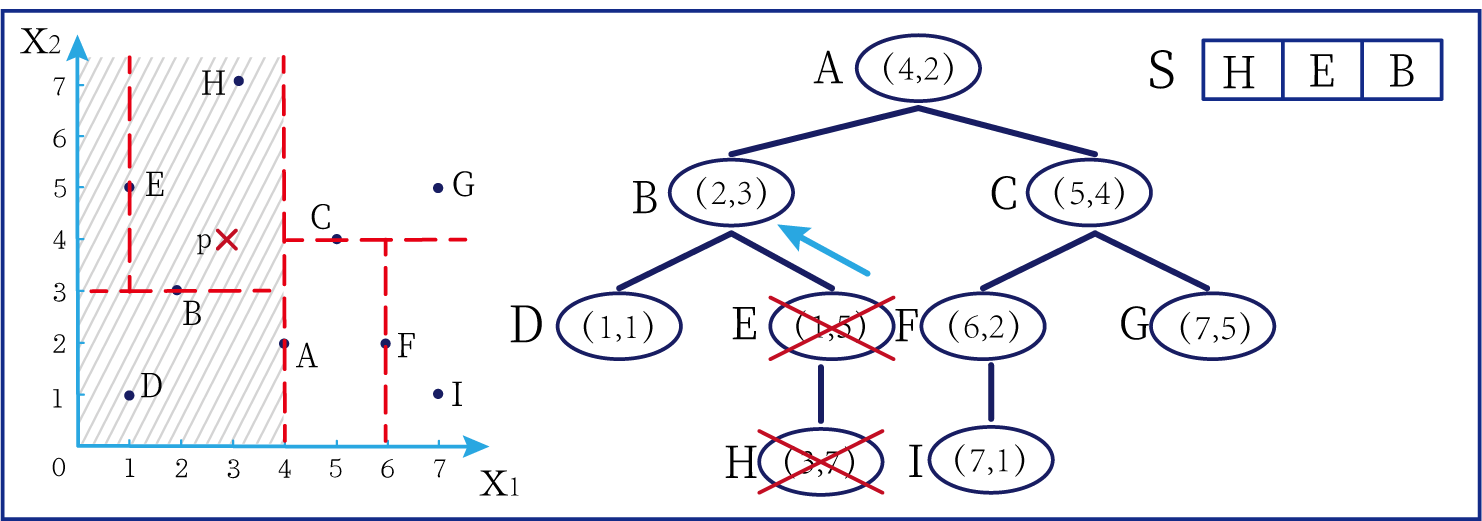
在上图中左边坐标轴中对应的是左上角阴影部分的区域，阴影区域扩大，说明接下来要扩大搜索范围搜索尚未搜索过的区域。此外，S中存入了B结点；E结点从kd树上划去，之后不再进行搜索。

• 第六步：
• 下面计算p点与B点的切分线距离。由于$P\hat{B}=|4-3|=1$，这个值小于p点到S中H、E、B三点距离的最大距离，所以此时需要从结点B另一子结点D进行搜索。

下面解释一下为什么要计算切分线距离（点到直线的距离）：

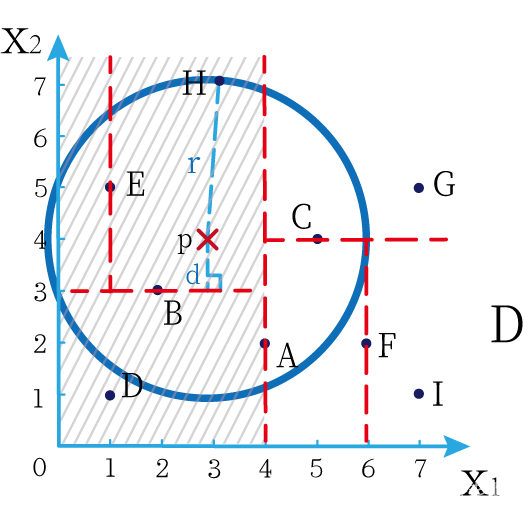
如上图，S中距离p点最远的一个结点是H点，以p为圆心，pH为半径画一个圆。记此时p到B的切分线距离为d。根据直线与圆的位置关系，当$d<r$的时候，平行于$x_1$轴且过B点的直线与圆相割。这说明圆的一部分在B点下方，而B点下方也有可能有点在圆内，所以要去B点下方去搜索。而这种搜索对应在kd树中就是搜索B结点的另外一个分支。

• 第七步：
• 重复第二步的步骤，对结点D进行搜索。由于结点D是叶结点，无法再继续搜索，所以我们计算pD的距离$pD=\sqrt{(3-1{)}^2+(4-1^2)}=\sqrt{13}$，将其与S中的距离比较。由于$pD=\sqrt{13}>3=pH>pE>pB$，所以不将D替换S中的点（即D点不可能是k近邻点）。

在上图中左边坐标轴中对应的是左下角阴影部分的区域，这是接下来要搜索的区域。

• 第八步：
• 标记点D为已访问结点，并退回上一结点进行搜索。发现结点B已被标记过，于是继续退回上一结点。此时重复第六步的操作，计算p点到A结点的切分线距离$pA=1$，小于$pH、pE、pB$的距离所以仍然需要搜索根结点A的另外一个分支。

• 第九步：
• 标记A为已访问结点，并将$pA$的距离与S中的进行比较，发现$pA<pH$，于是将A替换掉H。重复之前的步骤继续进行访问，最终得到如下结果：

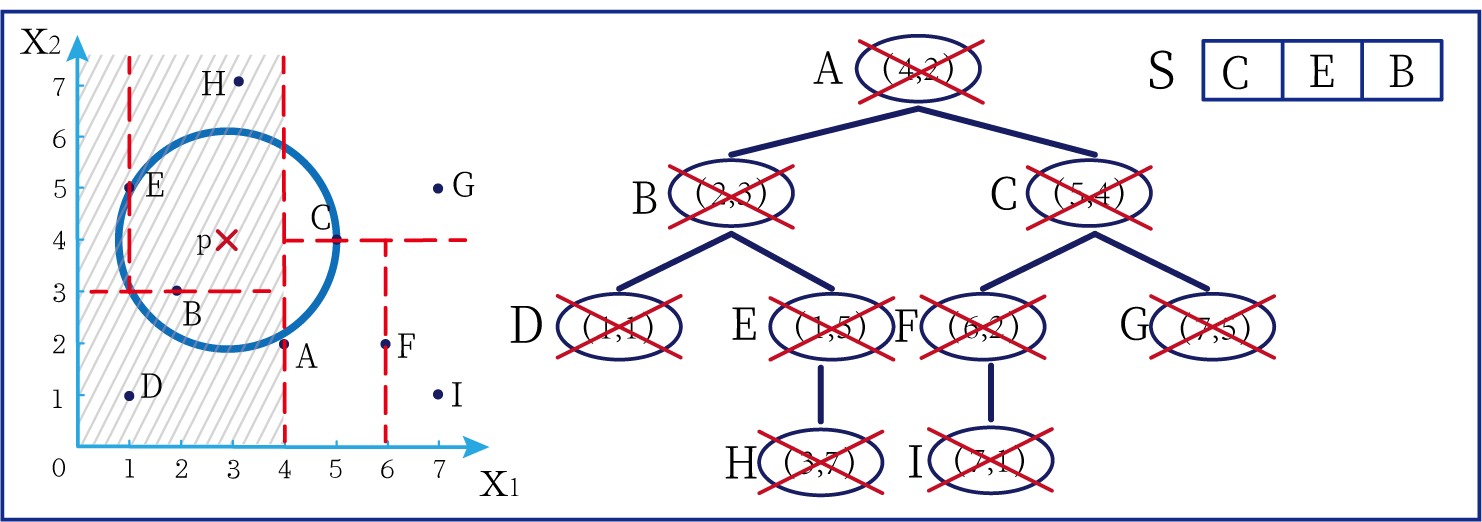
介于此题情况特殊，$pE=pA$，任意选一个可能会影响到最终的分类结果，但是在实际情况中，这种情况发生概率较小，如果发生，可能要重新设置k值再次进行搜索。

这样我们就完成了kd树的建立与搜索得到k个近邻点。

或许你并没有觉得这种方法简化了计算，但事实上，对于一个巨大的数据集，如果能够少遍历一棵子树，将会带来巨大的简便，只不过，这种情况是有概率性出现的。

如上图，如果通过kd树算法能够删去一条子树，那么其子树下面的结点都无需遍历。而这种遍历性来自于第六步的操作，即通过比较切分线大小来判断是否需要遍历子树。

算法描述

1. 根据p的坐标和kd树的结点向下进行搜索。如果p的坐标小于c，则走左子结点，否则走右子结点 【第一步】

2. 到达叶子结点时，将其标记为已访问。如果S中不足k个点，则将该结点加入到S中**【第三步】**；如果S不空且当前结点与p点的距离小于S中最长的距离，则用当前结点替换S中离p最远的点

3. 如果当前结点不是根节点，执行（a）；否则，结束算法

（a）回退到当前结点的父结点，此时的结点为当前结点（回退之后的结点）。将当前结点标记为已访问，执行（b）和（c）【第四步】；如果当前结点已经被访过，再次执行（a）。

（b）如果此时S中不足k个点，则将当前结点加入到S中 【第五步】；如果S中已有k个点，且当前结点与p点的距离小于S中最长距离，则用当前结点替换S中距离最远的点。

（c）计算p点和当前结点切分线的距离。如果该距离大于等于S中距离p最远的距离并且S中已有k个点，执行3 【第七步】；如果该距离小于S中最远的距离或S中没有k个点，从当前结点的另一子节点开始执行1 【第八步】；如果当前结点没有另一子结点，执行3。