目录
SIFT尺度不变特征变换
1. SIFT方法简介
SIFT(Scale-Invariant Feature Transform),即尺度不变特征变换,是一种计算机视觉的特征提取算法,用来侦测与描述图像中的局部特征。实质上,它是在不同的尺度空间上查找关键点(特征点),并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出、不会因光照、仿射变换和噪音等因素而变化的点,如角点、边缘点、暗区的亮点及亮区的暗点等。
概括如下:
- SIFT的全称是Scale Invariant Feature Transform(尺度不变特征变换),是由加拿大教授David G.Lowe在1999年发表于计算机视觉国际会议,2004年发表在IJCV上,是计算机视觉界近二十年来引用率最高的文章之一
- SIFT特征对旋转、尺度缩放、亮度变化等保持不变性,是一种稳定的局部特征
- SIFT的特征提取方面对计算机视觉近年来的发展影响深远,特别是几乎影响到了后续所有的角点提取和匹配算法
- 图像的局部特征,对旋转、尺度缩放、亮度变化保持不变,对视角变化、仿射变换、噪声也保持一定程度的稳定性
- SIFT变换最后提取出来的不仅仅是一个角点,实际上是一个特征描述子,是一个高维的向量
- 独特性好,信息量丰富,适用于海量特征库进行快速、准确的匹配
- 改进后的SIFT算法可以达到时时计算的速度
- 多量性:即使是很少几个物体也可以产生大量的SIFT特征
- 高速性:改进的SIFT匹配算法甚至可以达到实时性
- 扩展性:可以很方便的与其他的特征向量进行联合,形成一个新的特征描述
2. SIFT特征提取步骤
1. 尺度空间的极值检测
尺度空间指一个变化尺度( σ σ σ)的二维高斯函数 G ( x , y , σ ) G(x,y,σ) G(x,y,σ)与原图像 I ( x , y ) I(x,y) I(x,y)卷积(即高斯模糊)后形成的空间,尺度不变特征应该既是空间域上又是尺度域上的局部极值。极值检测的大致原理是根据不同尺度下的高斯模糊化图像差异(Difference of Gaussians,DoG),即建立高斯差分金字塔寻找局部极值,这些找到的极值所对应的点被称为关键点或特征点。
2. 关键点定位
在不同尺寸空间下可能找出过多的关键点,有些关键点可能相对不易辨识或易受噪声干扰。该步借由关键点附近像素的信息、关键点的尺寸、关键点的主曲率来定位各个关键点,借此消除位于边上或是易受噪声干扰的关键点。
3. 方向分配
为了使描述符具有旋转不变性,需要利用图像的局部特征为给每一个关键点分配一个基准方向。通过计算关键点局部邻域的方向直方图,寻找直方图中最大值的方向作为关键点的主方向。
4. 关键点描述子
找到关键点的位置、尺寸并赋予关键点方向后,将可确保其移动、缩放、旋转的不变性。此外还需要为关键点建立一个描述子向量,使其在不同光线与视角下皆能保持其不变性。SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象,具有唯一性。Lowe在原论文中建议描述子使用在关键点尺度空间内44的窗口中计算的8个方向的梯度信息,共 44 × 8 = 128 44 \times 8=128 44×8=128维向量表征。(opencv中实现的也是128维)
3. 构建尺度空间
3.1 尺度空间的概念
尺度空间是一个比较晦涩的概念,但尺度空间在自然空间中又是真实存在的,这里我们先从尺度谈起,在自然界物体都是由大小不同的实体组成,我们描述着些实体比如说房子、桌子一般会说有多高或者有多大,那么这个多高和多大一般所说就是长度和占地面积。在肉眼可见的情况下,我们常用厘米、米这样的标量尺度来描述长度和占地面积。而很少用纳米和微米这样很小的尺度。也就是说尺度是用来衡量一个量的一个标准。即我们可以用厘米来描述一个桌子多高,也可以用纳米来描述(当然生活中是没必要的)。往往大尺度下关注的是物体的全局信息,如物体的轮廓等,小尺度下则更注重物体的细节。
以上,对现实中物体的描述一定要在一个十分重要的前提下进行,即对自然界建模时的尺度。当我们用一个机器视觉系统分析未知场景时,计算机没有办法预先知道图像中物体尺度,因此我们需要同时考虑图像在多尺度下的描述,获知感兴趣物体的最佳尺度。图像的尺度空间表达指的就是图像在所有尺度下的描述。
3.2 图像多尺度表述
3.2.1 图像金字塔
图像的多尺度通常使用图像金字塔表述。图像金字塔是同一图象在不同的分辨率下得到的一组结果,其生成主要包括两种方式————下采样和上采样。
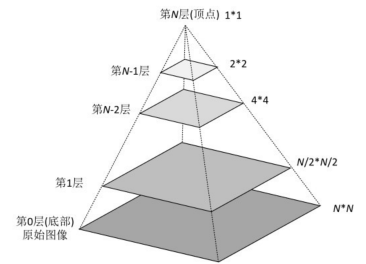
获得下采样金字塔一般有两个步骤:1. 利用滤波器处理图像;2. 对滤波图像进行下采样。
可以采用的滤波操作有很多,如邻域平均(可生成平均值金字塔),高斯低通滤波器(可生成高斯金字塔),带通滤波器(可生成拉普拉斯金字塔),或者不进行滤波(生成子抽样金字塔)。生成近似值的质量是所选滤波器的函数,与滤波器相关。如果没有使用滤波器,在金字塔的上一层中的混淆将变得很显著,子抽样点对所选取的区域没有很好的代表性。
获得上采样金字塔一般采用插值的方法。
3.2.2 高斯金字塔
并非任何低通滤波器都可用于生成尺度空间。可用于生成尺度空间的滤波器必须满足以下一点:由该平滑滤波器生成的粗尺度图像(高层图像)不会引入不存在于细尺度图像(低层图像)中的杂散结构。换言之,给定粗尺度图像中的任何一个区域,细尺度图像上总能找到相应的区域。这两个区域相比,粗尺度图像区域不能够有新的结构。
受制于尺度空间公理,高斯卷积核是实现尺度变换的唯一线性核(Lindeberg等人已经证明过)。而且不同的高斯核组成的尺度空间具有半群结构、尺度不变性和旋转不变性等。当金字塔的核为高斯核时,我们称为高斯金字塔,如下图所示。
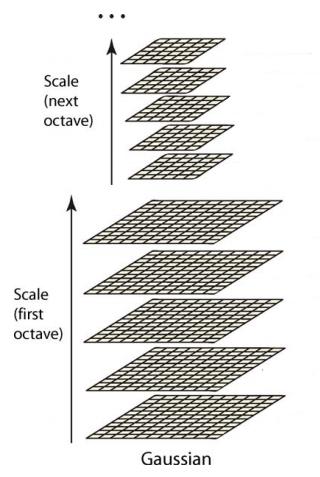
二维图像 I ( x , y ) I(x,y) I(x,y)的高斯金字塔尺度空间 L ( x , y , σ ) L(x,y,\sigma) L(x,y,σ)表示为:
L ( x , y , σ ) = I ( x , y ) ∗ G ( x , y , σ ) L(x,y,\sigma) = I(x,y) \ast G(x,y,\sigma) L(x,y,σ)=I(x,y)∗G(x,y,σ)
其中 G ( x , y , σ ) G(x,y,\sigma) G(x,y,σ)是尺度可变的高斯核函数, σ \sigma σ在高斯函数中为正态分布的标准差。在用高斯金字塔表示尺度形式时 σ \sigma σ被称为尺度大小, σ \sigma σ大小决定图像的平滑程度,大尺度对应图像的概貌特征,小尺度对应图像的细节特征:
G ( x , y , σ ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x,y,\sigma) = \frac{1}{2 \pi \sigma^2}e^{-\frac{x^2+y^2}{2 \sigma^2}} G(x,y,σ)=2πσ21e−2σ2x2+y2
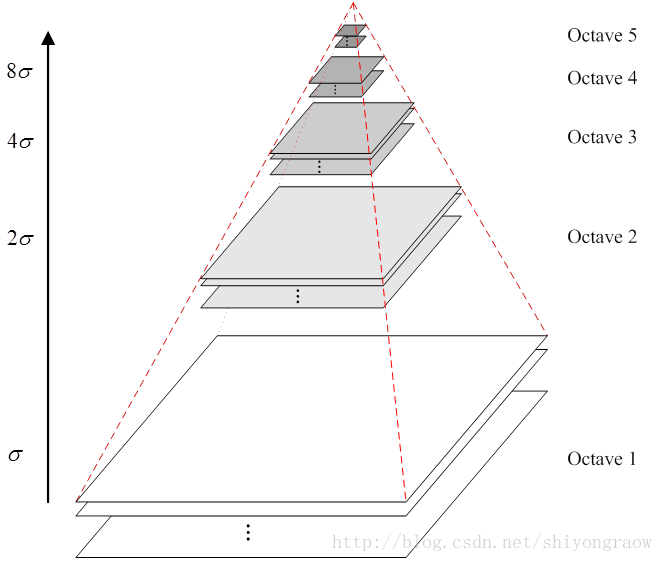
通过不同尺度的高斯核对原始图像进行卷积,卷积过后得到最下方的Octave1图组。而高斯金字塔上方的Octave2图组是由Octave1图组进行隔点取点下采样后,再用不同尺度的高斯核进行卷积得到的。
对于任意高斯金字塔,假设存在 i i i组(octave),每一组又含有 s s s层(一般为3~5层),它们的尺度参数互不相同,又存在一定的关系。第1组第1层的尺度参数为 σ \sigma σ,Lowe认为最优的 σ = 1.6 \sigma=1.6 σ=1.6。则其他层的尺度参数 σ ( i , s ) \sigma(i,s) σ(i,s)可表示为:
σ ( i , s ) = 2 i − 1 ⋅ k s − 1 ⋅ σ , k = 2 1 s \sigma(i,s) = 2^{i-1} \cdot k^{s-1} \cdot \sigma,\space k=2^{\frac{1}{s}} σ(i,s)=2i−1⋅ks−1⋅σ, k=2s1
3.2.3 高斯差分金字塔
在Lindeberg的论文《Scale-space theory: A basic tool for analysing structures at different scales》 指出尺度规范化的LoG算子具有真正的尺度不变性。即我们可以在不同尺度的图像(已经经过高斯卷积)上进行拉普拉斯运算(二阶导数),并求极值点,从而求出关键点。但这样做运算很大,Lowe做了近似处理。将高斯差分算子DoG近似于高斯-拉普拉斯算子LoG。
Laplacian of Gaussian(LoG)
Laplace算子通过对图像求取二阶导数的零交叉点(zero-cross)来进行边缘检测,其计算公式如下:
∇ 2 f ( x , y ) = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^2 f(x,y) = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} ∇2f(x,y)=∂x2∂2f+∂y2∂2f
由于微分运算对噪声比较敏感,可以先对图像进行高斯平滑滤波,再使用Laplace算子进行边缘检测,以降低噪声的影响。由此便形成了用于极值点检测的LoG算子。
∇ 2 [ G σ ( x , y ) ∗ f ( x , y ) ] = ∇ 2 [ G σ ( x , y ) ] ∗ f ( x , y ) = L o G ∗ f ( x , y ) \nabla^2 [G_{\sigma}(x,y) \ast f(x,y)] = \nabla^2 [G_{\sigma}(x,y)] \ast f(x,y) = LoG \ast f(x,y) ∇2[Gσ(x,y)∗f(x,y)]=∇2[Gσ(x,y)]∗f(x,y)=LoG∗f(x,y)
L o G = ∇ 2 [ G σ ( x , y ) ] = ∂ 2 G σ ( x , y ) ∂ x 2 + ∂ 2 G σ ( x , y ) ∂ y 2 = x 2 + y 2 − 2 σ 2 σ 4 ⋅ 1 2 π σ 2 ⋅ e − x 2 + y 2 2 σ 2 = 1 σ 2 ( x 2 + y 2 σ 2 − 2 ) ⋅ 1 2 π σ 2 ⋅ e − x 2 + y 2 2 σ 2 LoG = \nabla^2 [G_{\sigma}(x,y)] = \frac{\partial^2 G_{\sigma}(x,y)}{\partial x^2} + \frac{\partial^2 G_{\sigma}(x,y)}{\partial y^2} = \frac{x^2+y^2-2 \sigma^2}{\sigma^4} \cdot \frac{1}{2 \pi \sigma^2} \cdot e^{-\frac{x^2+y^2}{2 \sigma^2}} = \frac{1}{\sigma^2} \left (\frac{x^2+y^2}{\sigma^2}-2 \right ) \cdot \frac{1}{2 \pi \sigma^2} \cdot e^{-\frac{x^2+y^2}{2\sigma^2}} LoG=∇2[Gσ(x,y)]=∂x2∂2Gσ(x,y)+∂y2∂2Gσ(x,y)=σ4x2+y2−2σ2⋅2πσ21⋅e−2σ2x2+y2=σ21(σ2x2+y2−2)⋅2πσ21⋅e−2σ2x2+y2
Difference of Gaussian(DoG)
DoG算子是高斯函数的差分,具体到图像中,就是将图像在不同参数下的高斯滤波结果相减,得到差分图:
G σ 1 ∗ f ( x , y ) − G σ 2 ∗ f ( x , y ) = ( G σ 1 − G σ 2 ) ∗ f ( x , y ) = D o G ∗ f ( x , y ) G_{\sigma_1} \ast f(x,y) - G_{\sigma_2} \ast f(x,y) = (G_{\sigma_1} - G_{\sigma_2}) \ast f(x,y) = DoG \ast f(x,y) Gσ1∗f(x,y)−Gσ2∗f(x,y)=(Gσ1−Gσ2)∗f(x,y)=DoG∗f(x,y)
D o G ≜ G σ 1 − G σ 2 = 1 2 π ( 1 σ 1 2 e − ( x 2 + y 2 ) / 2 σ 1 2 − 1 σ 2 2 e − ( x 2 + y 2 ) / 2 σ 2 2 ) DoG \triangleq G_{\sigma_1} - G_{\sigma_2} = \frac{1}{2 \pi} \left ( \frac{1}{\sigma_1^2}e^{-(x^2+y^2)/2 \sigma_1^2} - \frac{1}{\sigma_2^2}e^{-(x^2+y^2)/2 \sigma_2^2} \right ) DoG≜Gσ1−Gσ2=2π1(σ121e−(x2+y2)/2σ12−σ221e−(x2+y2)/2σ22)
又因为:
∂ G σ ∂ σ = 1 σ ( x 2 + y 2 σ 2 − 2 ) ⋅ 1 2 π σ 2 ⋅ e − x 2 + y 2 2 σ 2 = σ L o G ≈ G ( x , y , k σ ) − G ( x , y , σ ) k σ − σ \frac{\partial G_{\sigma}}{\partial \sigma} = \frac{1}{\sigma} \left (\frac{x^2+y^2}{\sigma^2}-2 \right ) \cdot \frac{1}{2 \pi \sigma^2} \cdot e^{-\frac{x^2+y^2}{2\sigma^2}} = \sigma LoG \approx \frac{G(x,y,k \sigma)-G(x,y,\sigma)}{k \sigma - \sigma} ∂σ∂Gσ=σ1(σ2x2+y2−2)⋅2πσ21⋅e−2σ2x2+y2=σLoG≈kσ−σG(x,y,kσ)−G(x,y,σ)
D o G = ( k − 1 ) σ 2 L o G DoG = (k-1) \sigma^2 LoG DoG=(k−1)σ2LoG
其中 k − 1 k−1 k−1是个常数,不影响极值点的检测,LoG算子和DoG算子的函数波形对比如下图所示,由于高斯差分的计算更加简单,因此可用DoG算子近似替代LoG算子。
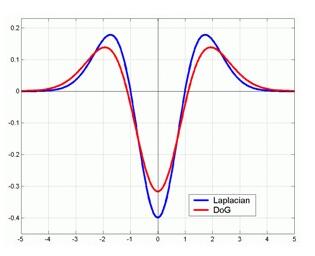
构建高斯差分金字塔
由于DoG算子是LoG算子的近似,可以用来极值检测,于是我们构建的高斯差分金字塔具有重要意义。二维图像 I ( x , y ) I(x,y) I(x,y)的高斯差分金字塔尺度空间 D ( x , y , σ ) D(x,y,\sigma) D(x,y,σ)表示为:
D ( x , y , σ ) = D o G ∗ I ( x , y ) = ( G σ 1 − G σ 2 ) ∗ I ( x , y ) = L ( x , y , k σ ) − L ( x , y , σ ) D(x,y,\sigma) = DoG \ast I(x,y) = (G_{\sigma_1} - G_{\sigma_2}) \ast I(x,y) = L(x,y,k \sigma) - L(x,y,\sigma) D(x,y,σ)=DoG∗I(x,y)=(Gσ1−Gσ2)∗I(x,y)=L(x,y,kσ)−L(x,y,σ)
由上所述,高斯差分金字塔可由高斯金字塔每组相邻层数作差得到。
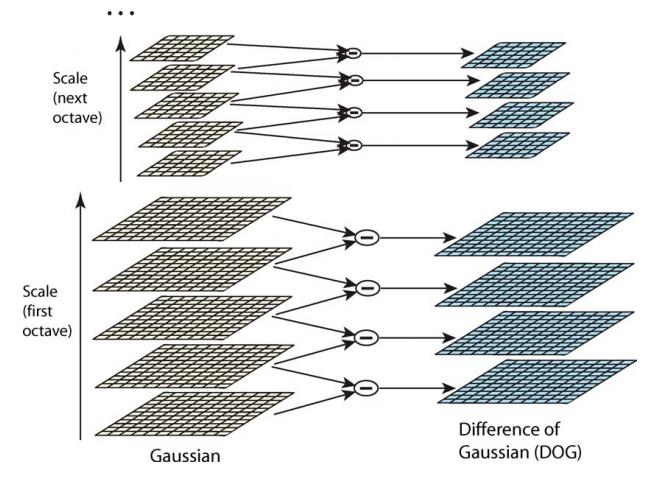
3.3 尺度空间的极值检测
为了寻找DoG函数的极值点, 每一个像素点要和它所有的相邻点比较,看其是否比它的图像域和尺度域的相邻点大或者小。如图所示,中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。一个点如果在DoG尺度空间本层以及上下两层的26个邻域中是最大或最小值时,就认为该点是图像在该尺度下的一个特征点


在极值比较的过程中,每一组图像的首末两层是无法进行极值比较的,为了满足尺度变化的连续性,我们在每一组图像的顶层继续用高斯模糊生成了 3 幅图像,高斯金字塔有每组S+3层图像。DoG金字塔每组有S+2层图像。
什么是尺度变化的连续性??
假设 s = 3 s=3 s=3,也就是每个塔里有3层,则 k = 2 1 / s = 2 1 / 3 k=2^{1/s}=2^{1/3} k=21/s=21/3,那么按照上图可得Gauss Space和DoG space 分别有3个(s个)和2个(s-1个)分量,在DoG space中,1st-octave两项分别是 σ , k σ \sigma,k\sigma σ,kσ,2nd-octave两项分别是 2 σ , 2 k σ 2\sigma,2k\sigma 2σ,2kσ;由于无法比较极值,我们必须在高斯空间继续添加高斯模糊项,使得形成 σ , k σ , k 2 σ , k 3 σ , k 4 σ \sigma,k \sigma,k^2 \sigma,k^3 \sigma,k^4 \sigma σ,kσ,k2σ,k3σ,k4σ这样就可以选择DoG space中的中间三项 k σ , k 2 σ , k 3 σ k \sigma,k^2 \sigma,k^3 \sigma kσ,k2σ,k3σ(只有左右都有才能有极值),那么下一octave中(由上一层降采样获得)所得三项即为 2 k σ , 2 k 2 σ , 2 k 3 σ 2k \sigma,2k^2 \sigma,2k^3 \sigma 2kσ,2k2σ,2k3σ,其首项 2 k σ = 2 4 / 3 σ 2k \sigma = 2^{4/3} \sigma 2kσ=24/3σ。刚好与上一octave末项 k 3 σ = 2 3 / 3 σ k3\sigma=2^{3/3} \sigma k3σ=23/3σ尺度变化连续起来,所以每次要在Gaussian space添加3项,每组(塔)共S+3层图像,相应的DoG金字塔有S+2层图像。
下一组的第一层图片如何得到??
下一组第一层的图片由上一组倒数第三层下采样得到。倒数第三层的尺度为 k s + 3 − 1 − 2 σ = ( 2 1 s ) s σ = 2 σ k^{s+3-1-2} \sigma = (2^{\frac{1}{s}})^{s} \sigma = 2 \sigma ks+3−1−2σ=(2s1)sσ=2σ,所以第二组第一层图片的尺度正好是第一组第一层的俩倍。
4. 关键点定位
上述离散空间中得到的极值点,不一定是真正极值点的位置,而是真正极值点附近的点。我们需要通过一定的方式得到亚像素精度的真正的极值点。同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应),以增强匹配稳定性、提高抗噪声能力。
4.1 关键点的精确定位
为了提高关键点的稳定性,需要对尺度空间DoG函数进行曲线拟合。利用DoG函数在尺度空间的Taylor展开式:
D ( x 0 + x ) = D ( x 0 ) + ( ∂ D ∂ x 0 ) T x + 1 2 x T ∂ 2 D ∂ x 0 2 x D(\mathbf x_0 + \mathbf x) = D(\mathbf x_0) + \left (\frac{\partial D}{\partial \mathbf x_0}\right )^T \mathbf x + \frac{1}{2} \mathbf x^T \frac{\partial^2 D}{\partial \mathbf x_0^2} \mathbf x D(x0+x)=D(x0)+(∂x0∂D)Tx+21xT∂x02∂2Dx
其中 D D D及其导数 ∂ D / x \partial D/\mathbf x ∂D/x在样本点 x 0 \mathbf x_0 x0处计算, x = ( x , y , σ ) T \mathbf x = (x,y,\sigma)^T x=(x,y,σ)T为相对 x 0 \mathbf x_0 x0的偏移量,将此二阶泰勒展示作为DoG函数的近似,对其求导并令导数为零,则可以得到极值点位置的偏移量。
∂ D ∂ x = ∂ D ∂ x 0 + ∂ 2 D ∂ x 0 2 x = 0 ⇒ x ^ = − ( ∂ 2 D ∂ x 0 2 ) − 1 ∂ D ∂ x 0 \frac{\partial D}{\partial \mathbf x} = \frac{\partial D}{\partial \mathbf x_0} + \frac{\partial^2 D}{\partial \mathbf x_0^2} \mathbf x = 0 \Rightarrow \hat{\mathbf x} = - \left ( \frac{\partial^2 D}{\partial \mathbf x_0^2} \right )^{-1} \frac{\partial D}{\partial \mathbf x_0} ∂x∂D=∂x0∂D+∂x02∂2Dx=0⇒x^=−(∂x02∂2D)−1∂x0∂D
D ( x 0 + x ^ ) = D ( x 0 ) + ( ∂ D ∂ x 0 ) T x ^ − 1 2 ( ∂ D ∂ x 0 ) T x ^ = D ( x 0 ) + 1 2 ( ∂ D ∂ x 0 ) T x ^ D(\mathbf x_0 + \hat{\mathbf x}) = D(\mathbf x_0) + \left (\frac{\partial D}{\partial \mathbf x_0}\right )^T \hat{\mathbf x} - \frac{1}{2} \left (\frac{\partial D}{\partial \mathbf x_0}\right )^T \hat{\mathbf x} = D(\mathbf x_0) + \frac{1}{2} \left (\frac{\partial D}{\partial \mathbf x_0}\right )^T \hat{\mathbf x} D(x0+x^)=D(x0)+(∂x0∂D)Tx^−21(∂x0∂D)Tx^=D(x0)+21(∂x0∂D)Tx^
当偏移量 x ^ \hat{\mathbf x} x^的任一维度上大于0.5,意味着真正的极值并不是离 x 0 \mathbf x_0 x0点最近,所以必须改变当前关键点的位置,同时在新的位置上反复插值直到收敛。如果这样做,也有可能超出所设定的迭代次数或者超出图像边界的范围,此时这样的点应该被删除。
极值处的函数值 D ( x 0 + x ^ ) D(\mathbf x_0 + \hat{\mathbf x}) D(x0+x^)可以用来去除低对比度的不稳定极值。在Lowe文献的实验中,所有 ∣ D ( x 0 + x ^ ) ∣ < 0.03 \left |D(\mathbf x_0 + \hat{\mathbf x})\right | < 0.03 ∣D(x0+x^)∣<0.03的极值点都被舍弃(图像已做归一化处理),Rob Hess等人实现时使用 0.04 / S 0.04/S 0.04/S。
4.2 消除边缘响应
为了提高关键点的稳定性,仅仅靠消除低对比度的点(DoG函数响应低)是不够的。由于DoG即使对边缘定位不准,也会有较强的响应值,因此就算是少量噪声也会引起特征点的不稳定。我们要消除不稳定的边缘响应。
DoG对于横跨边缘方向有较大的主曲率(变化率大),对于沿边缘方向(垂直于跨边缘方向)的响应主曲率较小。主曲率(二阶方向导数极大值)可以通过2x2Hessian矩阵求出。
H = [ D x x D x y D y x D y y ] \mathbf H = \begin{bmatrix} D_{xx}&D_{xy}\\D_{yx}&D_{yy} \end{bmatrix} H=[DxxDyxDxyDyy]
以上, D D D值可以通过求取邻点像元的差分得到。 H \mathbf H H的特征值与 D D D的主曲率成正比。这里避免求取具体的特征值,因为我们只关心特征值的比例。因此:
设 λ \lambda λ为Hessian矩阵的特征值。令 λ m a x = α , λ m i n = β \lambda_{max} = \alpha,\lambda_{min} = \beta λmax=α,λmin=β,可以得到:
T r ( H ) = D x x + D y y = α + β Tr(\mathbf H) = D_{xx} + D_{yy} = \alpha + \beta Tr(H)=Dxx+Dyy=α+β
D e t ( H ) = D x x D y y − ( D x y ) 2 = α β Det(\mathbf H) = D_{xx}D_{yy} - (D_{xy})^2 = \alpha \beta Det(H)=DxxDyy−(Dxy)2=αβ
如果 r r r为最大特征值与最小特征值之间的比值,即设 α = r ⋅ β \alpha = r \cdot \beta α=r⋅β,这样便有:
T r ( H ) 2 D e t ( H ) = ( α + β ) 2 α β = ( r β + β ) 2 r β 2 = ( r + 1 ) 2 r \frac{Tr(\mathbf H)^2}{Det(\mathbf H)} = \frac{(\alpha + \beta)^2}{\alpha \beta} = \frac{(r \beta + \beta)^2}{r \beta^2} = \frac{(r+1)^2}{r} Det(H)Tr(H)2=αβ(α+β)2=rβ2(rβ+β)2=r(r+1)2
这是一个“对勾”函数,当 r = 1 r=1 r=1时,即两个特征值相等时,函数值最小。若 D e t ( H ) < 0 Det(\mathbf H)<0 Det(H)<0,说明两个特征值已经异号了,也就是曲率肯定是不接近的,存在边缘效应,直接舍去X点。若 D e t ( H ) > 0 Det(\mathbf H)>0 Det(H)>0且 α > β \alpha > \beta α>β,说明 r > 1 r>1 r>1。而正由于 r ≥ 1 r \ge 1 r≥1,所以函数值随 r r r的增大而增大,是单调递增函数。于是,想要判断最大最小特征值的比值小于某一个值时,无需计算具体的特征值,只需计算Hessian矩阵的迹与行列式即可:
T r ( H ) 2 D e t ( H ) < ( r + 1 ) 2 r \frac{Tr(\mathbf H)^2}{Det(\mathbf H)} < \frac{(r+1)^2}{r} Det(H)Tr(H)2<r(r+1)2
Lowe在论文中给出 r = 10 r=10 r=10。也就是说,对于主曲率比值大于10的特征点将被删除,否则这些特征点将被保留。上述运算比求取矩阵H的具体特征值计算量要小的多。
5. 方向分配
在得到合适的特征点位置后,为每个特征点分配方向,用于描述子生成的基准,从而使描述子能实现图像旋转不变性,这也是我们SIFT第三步方向分配的主要目的。
5.1 计算梯度幅值和辐角
根据检测到的特征点的局部图像属性求得一个方向基准。我们使用图像梯度方向求取该局部结构的稳定方向。对于已经检测到的特征点,我们知道该特征点的尺度值 σ \sigma σ,根据这一尺度值,求得最接近这一尺度值的高斯图像,这样使所有的计算都能够以尺度不变的方式进行:
L ( x , y ) = G ( x , y , σ ) ∗ I ( x , y ) L(x,y) = G(x,y,\sigma) \ast I(x,y) L(x,y)=G(x,y,σ)∗I(x,y)
该特征点的梯度为:
L g r a d ( x , y ) = ( ∂ L ∂ x , ∂ L ∂ y ) L_{grad}(x,y) = \left ( \frac{\partial L}{\partial x},\frac{\partial L}{\partial y} \right ) Lgrad(x,y)=(∂x∂L,∂y∂L)
使用有限差分计算梯度的幅值和辐角:
m ( x , y ) = ( L ( x + 1 , y ) − L ( x − 1 , y ) ) 2 + ( L ( x , y + 1 ) − L ( x , y − 1 ) ) 2 m(x,y) = \sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2} m(x,y)=(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2
θ ( x , y ) = t a n − 1 ( ( L ( x , y + 1 ) − L ( x , y − 1 ) ) / ( L ( x + 1 , y ) − L ( x − 1 , y ) ) ) \theta(x,y) = tan^{-1}((L(x,y+1)-L(x,y-1))/(L(x+1,y)-L(x-1,y))) θ(x,y)=tan−1((L(x,y+1)−L(x,y−1))/(L(x+1,y)−L(x−1,y)))
根据尺度采样的 3 σ 3\sigma 3σ原则,以特征点为中心,计算 3 × 1.5 σ 3 \times 1.5\sigma 3×1.5σ( 1.5 σ 1.5 \sigma 1.5σ来源见下文)半径区域所有点梯度的幅值与辐角。
5.2 生成方向梯度直方图
将以上计算的特征点邻域梯度幅值根据梯度方向统计成直方图,梯度方向直方图的横轴是梯度方向角,纵轴是梯度方向角对应的梯度幅度累加值。方向直方图将360°方向分为36个bins,每个bin代表10°。直方图的峰值代表了该特征点邻域内图像梯度的主方向。
每个加入梯度直方图的采样点梯度幅值都要进行权重处理,加权采用圆形高斯加权函数,Lowe建议,其 σ \sigma σ值为特征点尺度的1.5倍。由于SIFT只考虑了尺度和旋转不变性,并没有考虑仿射不变性。通过高斯加权,使特征点附近的梯度幅值有较大的权重,这样可以弥补因没有仿射不变性而产生的特征点不稳定的问题。
如下是一个 8×8 的邻域,以直方图统计该邻域内的方向,计算出峰值方向,如下:
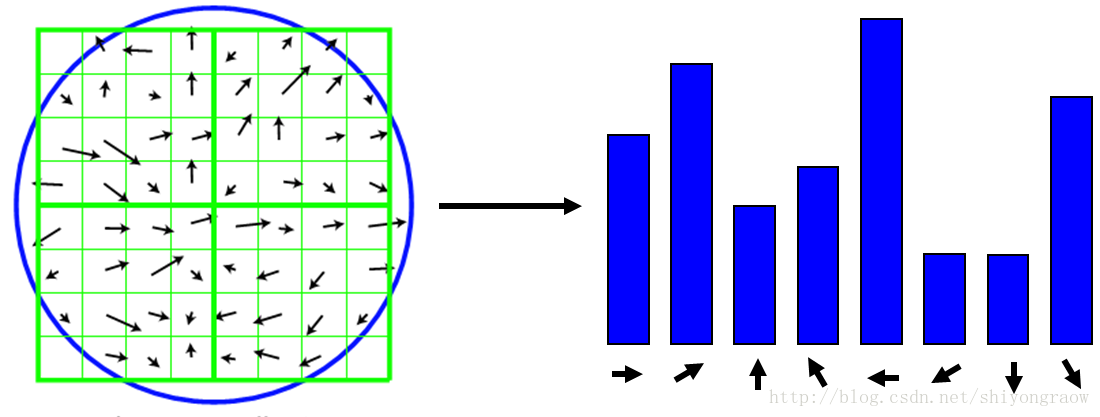
5.3 辅方向
梯度方向直方图中,当存在另一个相当于主峰值80%能量的峰值时,则将这个方向认为是该特征点的辅方向。一个特征点可能会被指定具有多个方向(一个主方向,一个以上辅方向),这可以增强匹配的鲁棒性,具体就是把该特征点复制成多份特征点,并将方向值分别赋给这些复制后的特征点。通常离散的梯度方向直方图进行插值拟合处理,对于每一个主方向或辅方向,都可以利用其相邻的3个直方插值,这样可以求得更精确的方向角度值。
以上,在获得了图像的特征点主方向后,每个特征点有三个信息 ( x , y , σ , θ ) (x,y,\sigma,\theta) (x,y,σ,θ):位置、尺度、方向,前俩个值是使用SIFT特征点检测得到的,特征点的主方向就是我们这一步求得的。
6. 特征描述
通过以上步骤,对于每一个关键点,拥有三个信息:位置、尺度以及方向。接下来就是为每个关键点建立一个描述符,用一组向量将这个关键点描述出来,使其不随各种变化而改变,比如光照变化、视角变化等等,以此来区别不同的关键点。这个描述子不但包括关键点,也包含关键点周围对其有贡献的像素点,并且描述符应该有较高的独特性,以便于提高特征点正确匹配的概率。
SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象,具有唯一性。表示步骤如下:
1. 确定生成描述子所用的区域
图中画的是 8 × 8 8 \times 8 8×8的窗口,形成 2 × 2 2 \times 2 2×2的描述子,实际Lowe在论文的实验中使用 16 × 16 16 \times 16 16×16的窗口,形成 4 × 4 4 \times 4 4×4的描述子,共 4 × 4 × 8 = 128 4 \times 4 \times 8=128 4×4×8=128维向量表征。
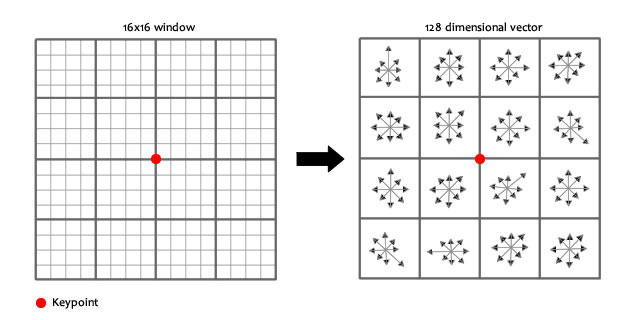
特征描述子与特征点所在的尺度有关,其生成描述子所用的区域也应该由尺度计算得到最佳的统计区域。将关键点附近的邻域划分成 d × d d \times d d×d个子区域(Lowe用的是 4 × 4 4 \times 4 4×4),每个子区域的大小与上一节为特征点分配方向时相同,使用 3 σ 3\sigma 3σ边长的子区域。
考虑到采样点实际不是对应整数像素,需要采用插值计算,所以需要向外至少拓展一格计算梯度幅值和方向,于是图像窗口的边长采用 3 σ × ( d + 1 ) o r 3 σ × d + 1 3 \sigma \times (d+1) \space or \space 3 \sigma \times d +1 3σ×(d+1) or 3σ×d+1???
再考虑到下一步要旋转坐标,直接取采样区域的外接圆直径 3 σ × ( d + 1 ) × 2 3 \sigma \times (d+1) \times \sqrt{2} 3σ×(d+1)×2,计算结果要取整。

图中的 m m m在Lowe的论文中取 3 3 3。
2. 将坐标轴旋转为关键点方向
由于描述子使用的是梯度方向,如果图像发生旋转,所有的梯度方向也会随之变化,对于每个关键点的描述子也就发生了变化。为了保持旋转不变性,我们在统计的时候将坐标轴旋转为对应关键点方向。(统计的区域随旋转是否发生变化,还是仅仅将每个采样点的方向减去关键点的方向,以统计与关键点的相对方向???)

原文中描述:为了实现方向不变性,将描述符的坐标和梯度的方向相对于关键点的方向进行旋转。为了提高效率,按照前一节所述的所有金字塔级别预先计算梯度。在图左侧的每个样本位置上都用小箭头表示。
若不改变统计区域,在不同旋转图像上统计的区域也会存在差别,所以需要相应旋转统计区域,而非像@utkarshsinha所描述的仅仅substracted from keypoint那样。而且在上一步确定采用区域时考虑到旋转于是扩大了统计半径。
旋转后的统计区域仍然是以关键点为中心的 16 × 16 16 \times 16 16×16的区域,而实际计算时存在两种思路:
- 根据旋转后要求的采样区域,逐行逐列扫描,寻找原图中(未旋转)对应的像素坐标点,得到该点的梯度幅值与方向。
- 对原图(未旋转)中的旋转不变区域——圆形区域(大于实际需要用到的矩形区域)进行逐行逐列扫描,按照旋转变化,变换到关键点坐标系,再通过除以子区域的边长 3 σ 3\sigma 3σ 得到其对应的子区域,再通过距离计算贡献值加入直方图统计中的bin。
这两种思路会造成计算和变换时方向的差别。选择第二种方法更好计算。
我们要采用图像像素坐标系,与关键点梯度方向的夹角为 θ \theta θ。则对于图像坐标系中的点 ( x , y ) (x,y) (x,y),在旋转后关键点坐标系中表示为 ( x ′ , y ′ ) (x',y') (x′,y′),相当于逆时针旋转 θ \theta θ,顺时针旋转 − θ -\theta −θ它们之间的转换关系用下式来表示:
[ x ′ y ′ ] = [ c o s θ − s i n θ s i n θ c o s θ ] [ x y ] \begin{bmatrix} x'\\y' \end{bmatrix} = \begin{bmatrix} cos\theta&-sin\theta\\sin\theta&cos\theta \end{bmatrix} \begin{bmatrix} x\\y\end{bmatrix} [x′y′]=[cosθsinθ−sinθcosθ][xy]
3. 计算梯度方向直方图
在每一个 4 × 4 4 \times 4 4×4的窗口内,计算梯度幅值和方向,将方向统计为8个bins的直方图。
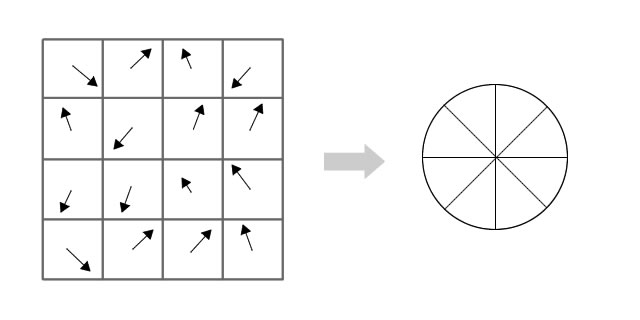
每个bin代表一个范围方向,梯度方向在 0 − 44 ° 0-44° 0−44°之间的加入第一个bin, 45 − 89 ° 45-89° 45−89°之间的加入第二个bin,以此类推。并且用于计算的数值(通常)取决于梯度幅值。还取决于采样点到关键点的距离。离关键点较远的梯度对直方图的贡献相应来说比较小。
这一点可以采用高斯加权函数来实现。使用窗口宽度一半( σ ′ = 0.5 × 3 σ \sigma' = 0.5 \times 3 \sigma σ′=0.5×3σ)的高斯加权函数为区域采样点分配权重,高斯窗口的目的是避免描述符的突然变化和窗口位置的微小变化,并且较少强调远离描述符中心的梯度,因为这些梯度受配准错误的影响最大。
w e i g h t = m ( x , y ) × e − ( x 2 + y 2 ) 2 × ( σ ′ ) 2 weight = m(x,y) \times e^{-\frac{(x^2+y^2)}{2 \times (\sigma')^2}} weight=m(x,y)×e−2×(σ′)2(x2+y2)
要求的采样点不是整数值,因此需要通过线性插值,正比于距离。
4. 归一化去除光照影响
如上统计的 4 × 4 × 8 = 128 4 \times 4 \times 8 = 128 4×4×8=128个梯度信息即为该关键点的特征向量。特征向量形成后,为了去除光照变化的影响,需要对它们进行归一化处理,便于不同图片同一特征点的比较。对于图像灰度值整体漂移,图像各点的梯度是邻域像素相减得到,所以也能去除。得到的描述子向量为 H = ( h 1 , h 2 , . . . , h 128 ) H=(h_1,h_2,...,h_{128}) H=(h1,h2,...,h128),归一化后的特征向量为 L = ( l 1 , l 2 , . . . , l 128 ) L=(l_1,l_2,...,l_{128}) L=(l1,l2,...,l128)则:
l i = h i ∑ j = 1 128 h j , j = 1 , 2 , 3 , . . . l_i = \frac{h_i}{\sqrt{\sum_{j=1}^{128} h_j}}, \space j=1,2,3,... li=∑j=1128hjhi, j=1,2,3,...
5. 描述子向量门限
非线性光照,相机饱和度变化对造成某些方向的梯度值过大,而对方向的影响微弱。因此设置门限值(向量归一化后,一般取0.2)截断较大的梯度值。然后,再进行一次归一化处理,提高特征的鉴别性。
6. 特征描述向量排序
按特征点的尺度对特征描述向量排序。
7. 特征匹配
特征点的匹配是通过两点集合内关键点描述子的比对来完成,描述子的相似度量采用欧氏距离。假设如下:
模板图中关键点描述子: R i = ( r i 1 , r i 2 , . . . , r i 128 ) R_i = (r_{i1},r_{i2},...,r_{i128}) Ri=(ri1,ri2,...,ri128)
实时图中关键点描述子: S i = ( s i 1 , s i 2 , . . . , s i 128 ) S_i = (s_{i1},s_{i2},...,s_{i128}) Si=(si1,si2,...,si128)
任意两描述子相似性度量: d ( R i , S i ) = ∑ j = 1 128 ( r i j − s i j ) 2 d(R_i,S_i) = \sqrt{\sum_{j=1}^{128} (r_{ij}-s_{ij})^2} d(Ri,Si)=∑j=1128(rij−sij)2
最终留下来的配对的关键点描述子,需要满足条件:
实时图中距离 R i 最近的点 S j 实时图中距离 R i 次最近的点 S p < T h r e s h o l d \frac{实时图中距离R_i最近的点S_j}{实时图中距离R_i次最近的点S_p} < Threshold 实时图中距离Ri次最近的点Sp实时图中距离Ri最近的点Sj<Threshold
8. SIFT的缺点
SIFT在图像的不变特征提取方面拥有无与伦比的优势,但并不完美,仍然存在:
- 实时性不高。
- 有时特征点较少。
- 对边缘光滑的目标无法准确提取特征点。
等缺点,如下图所示,对模糊的图像和边缘平滑的图像,检测出的特征点过少,对圆更是无能为力。近来不断有人改进,其中最著名的有SURF和CSIFT。
