一、定义

相关系数（correlation of coefficient）是统计学中的概念，是由统计学家卡尔·皮尔逊设计的一个统计指标，也称作 Pearson 相关系数。相关系数用于描述两个连续型变量之间的线性相关程度及相关方向，它的取值在 [-1, 1] 之间。

总体的 Pearson 相关系数用 $\rho$ 表示，计算公式为：

$\begin{align} \rho_{\textbf{x},\textbf{y}}&=\frac{cov(\textbf{x}, \textbf{y})}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber\\ &=\frac{E[(\textbf{x}-E[\textbf{x}])(\textbf{y}-E[\textbf{y})]}{\sigma_\textbf{x}\sigma_\textbf{y}} \nonumber\end{align}$

样本的 Pearson 相关系数用 $r$ 表示，计算公式为：

$\begin{align} r(\textbf{x}, \textbf{y})&=\frac{cov(\textbf{x}, \textbf{y})}{\sqrt{var(\textbf{x})var(\textbf{y})}}\nonumber\\ &=\frac{E[(\textbf{x}-\mu_\textbf{x})(\textbf{y}-\mu_\textbf{y})]\nonumber}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber\\ &=\frac{E[\textbf{x}\textbf{y}]-E[\mu_\textbf{x}\textbf{y}]-E[\mu_\textbf{y}\textbf{x}]+E[\mu_\textbf{y}\mu_\textbf{x}]}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber\\ &=\frac{E[\textbf{x}\textbf{y}]-E[\textbf{x}]E[\textbf{y}]-E[\textbf{y}]E[\textbf{x}]+E[\textbf{y}]E[\textbf{x}]}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber\\ &=\frac{E[\textbf{x}\textbf{y}]-E[\textbf{x}]E[\textbf{y}]}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber\\ &=\frac{E[\textbf{xy}]-E[\textbf{x}]E[\textbf{y}]}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber \end{align}$

Pearson 相关系数 = 两个变量的协方差除以标准差的乘积。

（参考：统计知识扫盲：相关系数）

（参考：协方差）

（参考：协方差公式推导）

二、特性

相关系数可以衡量两个变量之间的相关性大小；
相关系数的绝对值越接近1，表明两个变量之间的线性相关性越强；相关系数的绝对值越接近0，表明两个变量之间几乎不存在线性相关关系（但可能存在其他关系）；
在两个变量的位置、尺度单独变化下是不变的。即X和Y的相关系数和 aX+b 和 cY+d 的相关系数相等。

三、适用条件

两变量都是连续型变量；
两变量成对出现，且相互独立；
Pearson是积差相关系数，它只能说明变量之间的线性相关关系，只适用于线性相关的场景。对于非线性相关等复杂场景，Pearson相关系数无法描述两个变量的相关性程度；
Pearson相关系数是在原始数据的方差和协方差基础上计算得到的，所以对离群值很敏感，样本中存在的极端值/异常值对Pearson相关系数的影响很大，因此要慎重处理，必要时要进行剔除，或者加以变量转换，避免得出因一两个数值导致结果错误的结论；
Pearson积差相关系数要求相应的变量呈双变量正态分布，既要求两个变量各自服从正态分布，有要求两个变量服从一个联合的双变量正态分布。

以上三条，前两条要求最严，第三条比较宽松，违反时系数的结果也是比较稳健的。

（参考：Matlab 相关系数的计算与作图）

（参考：统计学习--三种常见的相关系数）

（参考：相关系数的数值范围及其判断标准是什么）

四、Matlab 仿真

% Matlab 中计算相关系数的命令

[r, p] = corr(x, y[, 'type', 'Pearson'])  % 等号右边的[]为可缺省项
[r, p] = corrcoef(x, y[, 'alpha', 0.95])

% 如果 X 和 Y 是序列，corr(X, Y) 和 corrcoef(X, Y) 都可以计算两个序列相关；如果是序列，使用 corr() 必须得是列向量！
% 如果 X 和 Y 是矩阵，corr(X, Y) 可以计算矩阵相关，但 corrcoef(X, Y) 会将其转换为序列再进行计算。

1. 时间序列

%% 时间序列的 Pearson 相关系数
clear; clc; close all; warning off;

% 序列
x = [15, 20, 25, 30, 35]';
y = [1, 4, 9, 16, 25]';

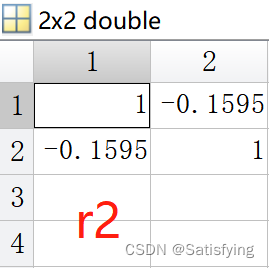
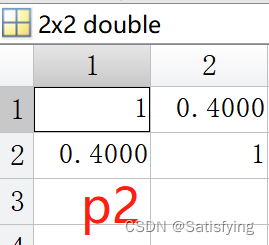
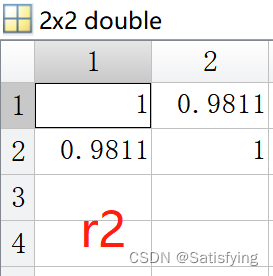
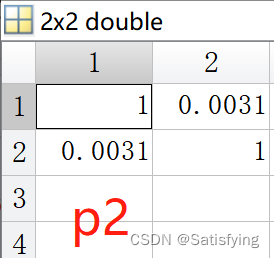
[r1, p1] = corr(x, y);  % 必须是列向量，行向量计算出来的结果不对！
[r2, p2] = corrcoef(x, y);  % 可以是行向量，也可以是列向量，结果一致

运行结果：

理论计算：

$\begin{align} \rho_{\textbf{x}, \textbf{y}}&=\frac{cov(\textbf{x}, \textbf{y})}{\sigma_\textbf{x}\sigma_\textbf{y}}\nonumber\\ &=\frac{\frac{1}{N}\sum_{i=1}^N\textbf{x}_i\textbf{y}_i-\frac{1}{N}\sum_{i=1}^N\textbf{x}_i\frac{1}{N}\sum_{i=1}^N\textbf{y}_i}{\sqrt{\frac{\sum_{i=1}^N(\textbf{x}_i-\mu_\textbf{x})^{2}}{N}\frac{\sum_{i=1}^N(\textbf{y}_i-\mu_\textbf{y})^{2}}{N}}}\nonumber\\ &=\frac{\frac{15+80+225+480+875}{5}-\frac{15+20+25+30+35}{5}\frac{1+4+9+16+25}{5}}{\frac{\sqrt{(100+25+0+25+100)(100+49+4+25+196)}}{5}}\nonumber\\ &=0.9811\nonumber \end{align}$

结论：

r2(1, 2) = r2(2, 1) = r1；
p2(1, 2) = p2(2, 1) = p1；
其中 r 为两个向量之间的相关系数，p 为非零相关的假设检验值（位置和 r 对应），p < 0.05 表示相关性显著；
Matlab 中的方差函数 var()、标准差函数 std()、相关系数函数 corr()、corrcoef() 都是用的样本的有偏估计计算的（即分别对应的样本的有偏方差、有偏标准差、用有偏标准差计算的相关系数）。

（参考：Matlab计算相关系数）

2. 矩阵

%% 矩阵的 Pearson 相关系数
clear; clc; close all; warning off;
rng('default');

% 矩阵
X = randn(10, 3);  % m列
Y = randn(10, 3);  % n列
Y(:, end) = sum(X, 2); 
Z = X - Y;  % m列
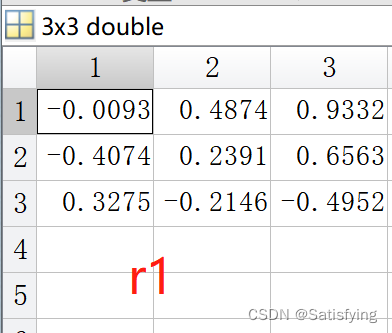
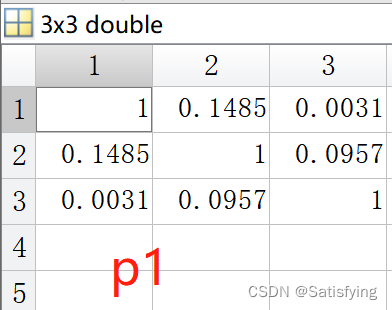
[r1, p1] = corr(X, Y);  % 分别计算矩阵X和矩阵Y每列的相关系数，结果是m*n大小的相关系数矩阵
[r2, p2] = corrcoef(X, Y);  % 错误的写法！出来结果是错的，corrcoef不能传入两个矩阵进行相关系数计算！
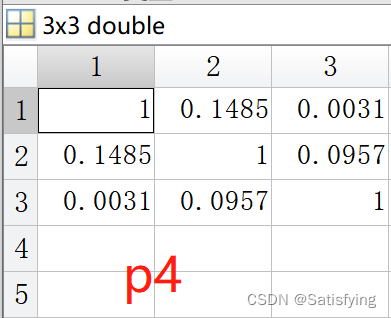
[r3, p3] = corr(Z);  % 分别计算z每列之间的相关系数，结果是m*m大小的相关系数矩阵
[r4, p4] = corrcoef(Z);  % 和r3/p3的结果一致