写在前面, ppt鸟语一堆实在看得我头痛…
离散数学高级版
文章目录
命题逻辑
命题逻辑 Propositional Logic
句法
逻辑:在计算机科学中对情景建模的语言,以促进对他们的形式推理
逻辑是基于陈述句语句
Prop. = Propositional 命题的
declarative sentences 陈述句
原子命题可用符号p,q,r,Φ表示
命题逻辑的syntax句法,下面是命题逻辑的递归定义
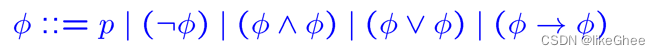
::= 定义
命题的合适公式 , 只有限次运用上述规则的命题称为well formed formulas
公式的解析树(树表示)
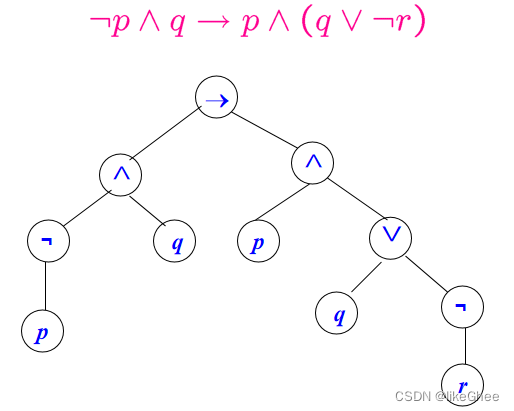
自然推理 命题逻辑证明理论
Natural Deduction 自然推理
命题逻辑的证明理论: 允许从现有的公式推出新的公式的证明规则集合
规则集合,基本规则如下
横线上的是条件,横线下是可推出的结论,红色标志是公式符号
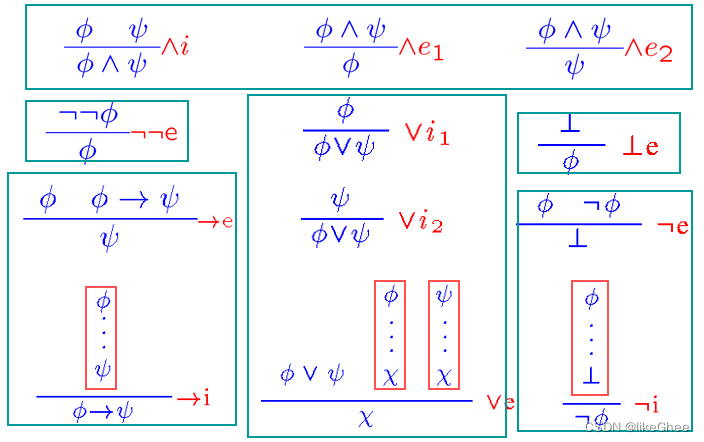
规则集合,一些衍生规则
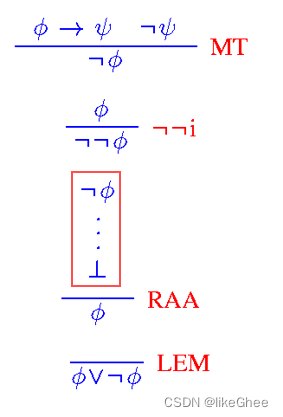
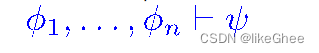
从命题Φ1,…Φn推出新命题φ
这个结构称为sequent(不知道怎么翻,后略说明)
如果能从现有的公式推出新的公式那么这个sequent是有效的
语义
命题逻辑的语义, the semantics
上面我们知道了,命题逻辑的句法可以表示为
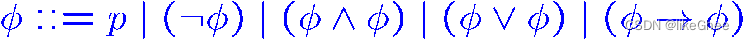
还知道了一系列的形式的推导规则
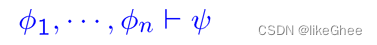
但是公式的意义是什么呢?
命题被赋予T/F值,那么所涉及的命题的真值可以用真值表表示
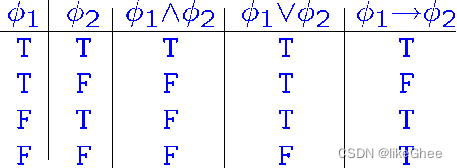
证明的语义表示对应物
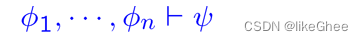
语义蕴含关系
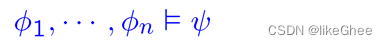
soundness: 如果一个论证形式有效且前提为真,那么这个论证就是可靠的,其中逻辑系统是可靠的(sound)当且仅当系统中可证明的每个公式对于系统的语义都是逻辑有效的
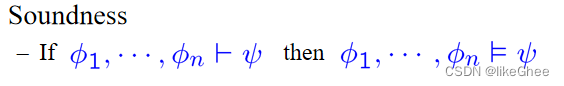
comleteness:如果具有某一性质的公式都可以用该系统推导出来,即是该系统的定理之一,则称该形式系统是完备的
直观地说,一个系统被称为完备的,它能推导出每一个正确的公式
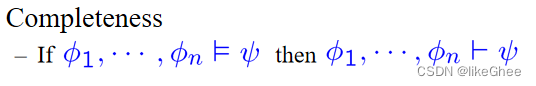
命题逻辑既是可靠的也是完备的
谓词逻辑及证明理论
从命题逻辑到谓词逻辑
有了命题逻辑,我们还需要更丰富的语言
命题逻辑研究陈述句,关于世界的每一个陈述句都可以被赋予一个真值,很好的处理了句子的组成部分,如非,并且,或者,如果那么,但是局限性是不能表达存在,所有,其中,当且仅当
那么一个命题可以用更好的逻辑结构来表示,引出了谓词逻辑
属性由谓词(Predicates)表示,如S
如S(Andy): Andy is a student, M(x,y):x is y’s mother
Andy是什么什么,就是赋了一个属性,可以用Predicates表示
变量(Variables)是一个具体的值的占位符
如S(x):x是一个学生
量词(Quantifiers)更好的表示短语,如果任一,存在量词(∀,∃ )
例子
没有一本书是气态的,字典是书,因此没有字典是气态的

Andy和Paul有同一个外祖母
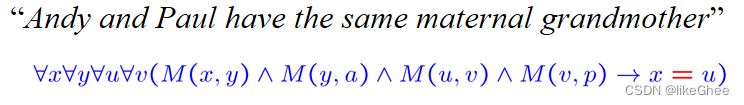
引入了等号谓词 =,那么上面的表达可以变成
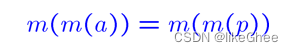
函数m(a):a的母亲,这样用函数func表示更合适,每一个人都有各自的一个母亲
B(x,y): x是y的兄弟,这个用谓词表示适合,因为每一个人可能不只一个兄弟
谓词逻辑形式语言
对谓词逻辑进行建模
(这部分根本不讲人话…)
谓词公式(predicate formula)中有两种东西, terms和formulas
terms: 如Andy,Paul,m(a)特指一个object,我们用terms来表示
formulas: 可以给出真值的表达式
谓语词汇*(predicate vocabulary)表由三组组成: P,F,C
谓词符号P
函数符号F
常量C
P,F都有一个固定大小的参数
谓词逻辑的形式语言的要素:
terms, formulas, 自由/受限变量, Substitution
Terms
terms术语*,我理解就是一个物体,抽象出来的obj
Terms定义为如下:
任何变量是一个terms
任何的常量C是一个terms
有n个terms,t1,…,tn,f是函数符号,那么f(t1,…,tn)是一个terms
巴科斯-诺尔范式(Backus-Naur Form)定义

上式注意的点是terms第一个组成部分是常量c和变量x,更复杂的terms是使用以前构建的terms再和函数符号构建出来
Formulas
formulas: 可以给出真值的表达式
用F,P定义的Formulas是归纳定义的,使用F上已经定义的terms
Formulas的定义
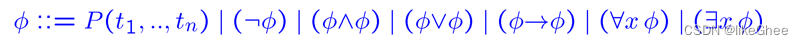
如果P是一个谓词, P具有n≥1个参数,且t1,…,tn是F的项,那么P(t1,…,tn)是一个公式 (formula)
Φ是一个表达式,那么非Φ也是一个表达式,这是一个递归定义,用到了之前的定义
如果两个formula,那么这两个formula的析取合取蕴含关系是formula
formula的任意存在关系也是formula
举个formula例子
我父亲的儿子都是我的兄弟
给出了两种表达

变量
变量的自由与受限
Φ是一个谓词逻辑的formula
如果说一个x在Φ中是自由的,那么x从叶子结点出发往上走没有遇到∀x或者∃x结点
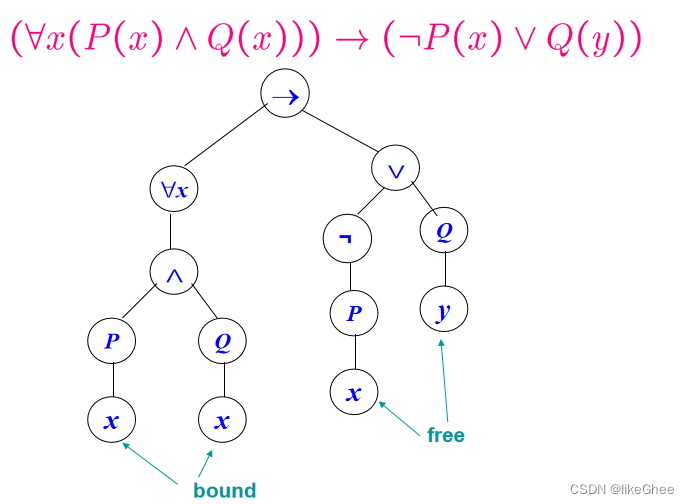
∀xΦ中变量x的作用域要减去它子表达式x的作用域,如下图红框中的x才是同一个作用域的
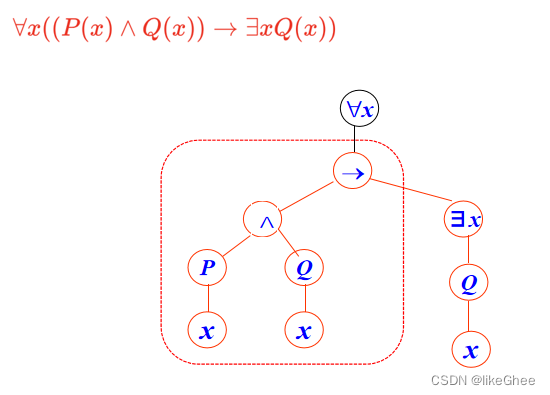
Substitution
变量只是占位符,所以我们必须有办法用更具体的信息来代替它们
给定 variable x, term t, formula Φ
定义 Φ[t/x] 为:将Φ中的自由变量x替换为t得到的表达式
下图为一个例子
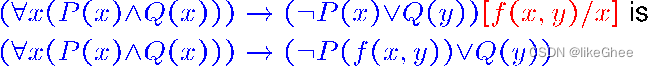
给定term t, variable x, formula Φ
t中有出现变量y, 要替换Φ中x, x应该不出现在有∀y或者∃y的作用域中,否则会产生不良影响
例子: 需要通过改写量词y的作用域中的变量y来实现替换,下面就将量词y替换成了z

t is free for x in Φ, 定义很绕:对t中出现的每个变量如v, 没有自由的x结点在v的量词作用域中,
换句话说就是:对t中出现的每个变量如v, 有自由的x结点在v的量词作用域中,t就不是自由的
那么再换句话说:对t中出现的每个变量如v, 所有自由的x结点不在v的量词作用域中,t就是自由的
所以首先能替换的前提是x是自由的结点,再考虑t替换后,是否存在t中出现的变量与作用域冲突
如果根本没有可以替换的自由结点,那么t也是自由的,这种是特殊的情况

例题:
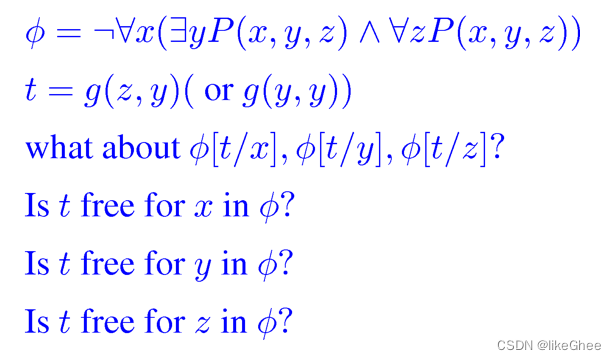
t = g(z, y)
第一种情况,命题Φ中t代替x,发现根本没有自由的变量x,所以替换不了,因此t是自由的对于x
第二种情况,命题Φ中t代替y,第二个谓词P的y可以替换,g(z,y)替换进去后,只考虑t中所有出现的变量即z和y,发现与z作用域冲突,有一个冲突,所以not free
第三种情况,命题Φ中t代替z,第一个谓词P中的z可以替换,g(z,y)替换进去后,只考虑t中存在的变量z和y,与y作用域冲突,与z作用域不冲突,有一个冲突,因此是not free
谓词逻辑的证明理论
证明理论: 规则集合,上面提到过了,证明理论是允许从现有的公式推出新的公式的证明规则集合
命题逻辑的自然推演规则依然有效
谓词逻辑的自然推导规则有:
命题逻辑规则
等号规则
全称量词和存在量词规则
量词的等价关系(量词规则)
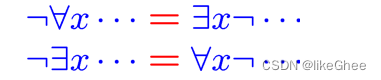
等号规则
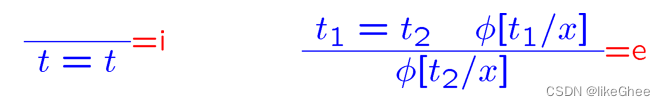
=e式中用到了t1=t2, 用一个整体的思维下面证明
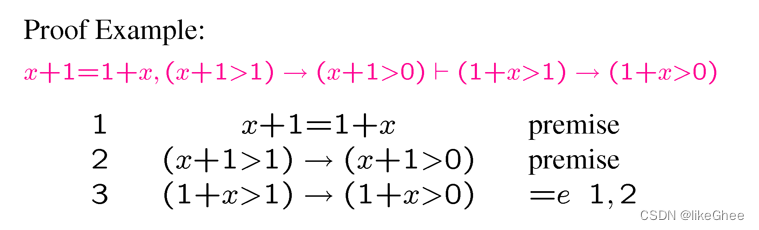
任意的消去和引入

存在量词的规则

例子: 比较综合的一题

谓词逻辑语义
在命题逻辑中,我们可以基于原子命题的T/F值给表达式一个T/F值
但是在谓词逻辑中呢,如下公式,在命题逻辑,我们可以给P(x)和Q(y)一个T/F值,来判断表达式的T/F值
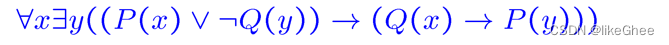
但是对于谓词逻辑在通常情况下,变量和谓词之间的关系和给原子命题分配的T/F值不能随机进行
因为我们需要考虑到量词关系
对于存在量词中的变量,如∃xΦ
我尝试找到一些具体的x值,存在一个值让表达式为T即可
而对于∀xΦ,需要判断对所有可能的x值让表达式为T,只有存在一个x不满足则为F
Models
函数符号F,谓词符号P,F和P的参数是固定大小的(不能有无限个参数)
(F,P)的model M定义为:

1.非空的集合A,域中的具体的值
2.F中所有的函数,An是A中元素组合得到的n个元组(a1,…,an),作为参数,An经过函数f得到值也要在A中包含,这样才完备
3.对于P中所有的谓词, 具体 P M P^M PM的值是An集合的子集,因为谓词逻辑输入是多个值,表示这些值之间的关系
对f, f M f^M fM 和P, P M P^M PM的区分
f M f^M fM 和 P M P^M PM 是抽象含义中的一个具体

举个具体的例子
F = {+, *, -}
P = { =, <=, <, zero}
对于model M定义为:
1.集合A,A是数值的空间域, A=全体实数R
2.F中所有函数,+,*,-,接收两个实数的参数,返回它们的相加,乘积,相减的值
3.P中的所有谓词,=,<=, < 表示等于,小于等于,小于,zero表示接收的参数r值为0
则任意y,只要y=0, 那么y乘任意实数都等于0,可以形成表达式:
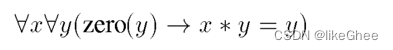
look-up table
对于谓词逻辑的表达式,我们尝试检查一个具体的情况是否满足表达式
我们给定一个 环境(env)look-up table来进一步说明一个特定情况下的表达式的关系
look-up table:将表达式变量到具体值的映射
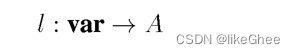
宏观上看是一个特定的环境,具体来看实现是通过look up table操作替换变量成具体值
定义env的更新操作
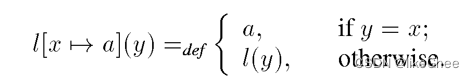
l[x -> a](y),当y=x,意思是把x变量替换成常量a
如果是其他变量,那就找那个变量的替换,比如y那就去看l(y)
The Satisfaction Relation
给定一个(F,P)的Model M,给定一个env l,我们定义一个满足关系,给定在关于env*l的Model中, 表达式Φ都为T,那么我们有下面的满足关系表达(satisfaction relation)
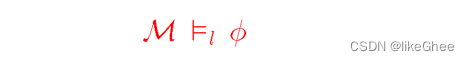

比如下面举一个例子, model有F和P和特定情景env,当loves={(a,a), (b,a), (c,a)}时,Φ不满足为T

给两个env l和l’ ,对Φ的自由变量替换都是相同的,l(x) = l’(x), 我们有以下成立: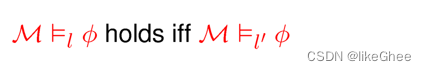
如果Φ没有自由的变量,那么Φ成立与是否是特定哪个env是无关了,对于这种情况,满足关系可以直接写成

Semantic Entailment
蕴含语义*
大概说的是谓词逻辑下的蕴含表达
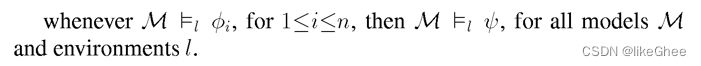
有若干表达式Φi, 在任何env和M下,Φi (1~n)都有满足关系,然后推出对应的M和l下,φ也有满足关系, 那么能如下进行表示:
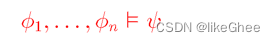
符号重载: 这时候这个符号表示为谓词逻辑下的蕴含预测(semantic entailment),而不是满足关系了
例子:大体上都是说谓词的量词值域和具体值之间应考虑统筹关系


Semantics of equality
等于语义
举个例子,数值域A
A={a,b,c},
有等于关系, = is {(a,a), (b,b), (c,c)}
Undecidability of predicate logic
谓词逻辑的不可测性
谓词逻辑中有效性的判定问题是不可定的(由A. Church在1936年证明)
谓词逻辑中的可满足性问题也是不可定的。
可证明性问题也是无法确定的:
这意味着,对于谓词逻辑一个人不能仅仅只靠机械地产生一个给定公式的证明, 实现定理证明或反驳。
也就是一个人仅仅只靠机械规则(程序式判断)不一定能证明或反驳给定的公式
Resolution
前章小结
上面我们已经提到了命题逻辑和谓词逻辑及其证明理论
命题逻辑和逻辑谓词的语义,如命题逻辑的真值表,
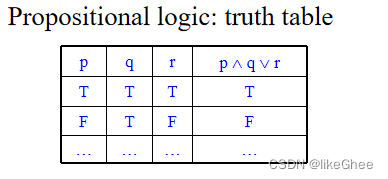
谓词的model的满足关系和验证
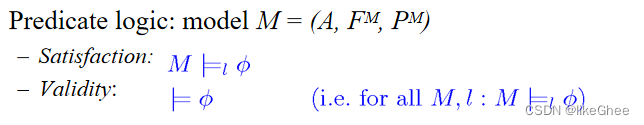
可靠性和完备性
Soundness and completeness
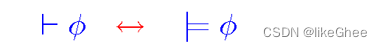
接下来我们将考虑有效性证明(validity), 有效性表达为:
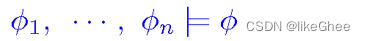
我们可以为公式找出一个证明或者检查这个公式是有效的
同等于验证将结论转为非后的不可满足性unsatisfiability
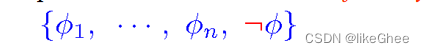
不可满足性(unsatisfiability):如果谓词公式P对于个体域D上的任何一个解释都取得真值F,则称P在D上是永假的;如果P在每个非空个体域上均永假,则称P永假。谓词公式的永假性又称为不可满足性或不相容性。
这就是Resolution所做的事情
Literal, Clause
说CNF前先明确两个概念
literal: 原子命题p,原子命题p的非
clause: 原子命题的析取组成
下面这个就是clause

析取是幂等的,交换的,结合的,因此一个clause可以被看作是一组不同的literal
clause存在命题的非 可以改写成蕴含形式
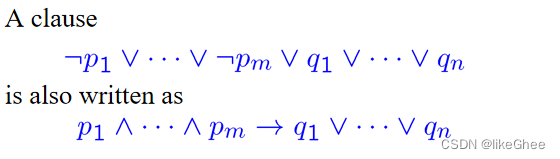
CNF
conjunctive normal form , CNF 合取范式

里面每个φ是clause,例子:
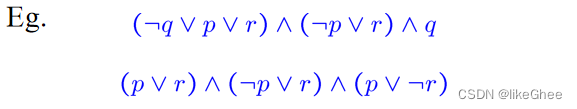
CNF公式可以看作是一串析取的合取连接。
如何转为CNF
1.否定词整理
2.修正-重命名绑定变量,以确保唯一性
3.去除量词 (Skolemisation )
4.转化为Clause
1.not符号(后简称not)只能出现在原子命题(后简称p)前面
我们需要展开蕴含->的地方
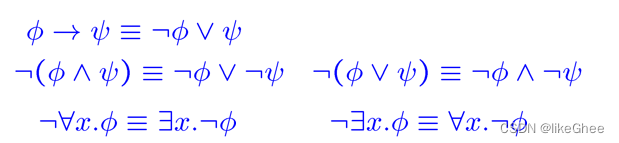
2.修正-重命名绑定变量,以确保唯一性
限制变量不能和自由变量重名
所有的限制变量必须不同
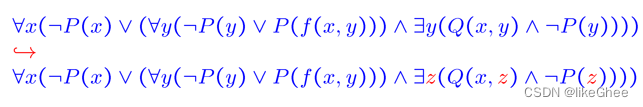
3.移除存在量词
引入新的常数和函数来替换与存在量化变量相对应的变量, 函数和常数不能在公式中已经存在
分两种情况, 存在在全程量词前面, 直接替换成一个新的常量
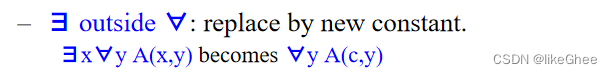
存在在全称量词里面,说明这个存在量词受限于全称量词, 见下面的x和w例子

在skolemisfication之后,我们将所有∀-量词移动到最前面或删除它们
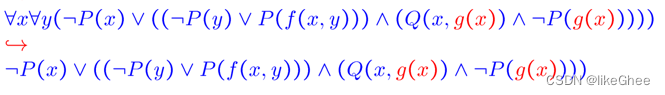
4.转为clause
可能会运用到分配律
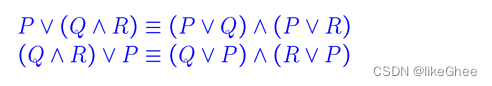
为什么我们需要CNF
算法的标准化输入
减少冗余和重复
CNF是解析(resolution)过程输入
Ground Resolution
Resolution 解析基于“矛盾证明”的思想
思想1.增加结论的否定作为假设;
思想2.如果结论有效,就会得到矛盾
思想3:消除多余的原子命题
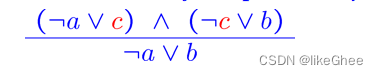
上面证明理论等价于
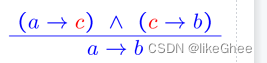
对于命题逻辑,称为ground resolution, 基础解析,写作下面的公式

Non-Ground Resolution
谓词逻辑的resolution称为Non-Ground Resolution
Non-Ground Resolution通常写法如下:
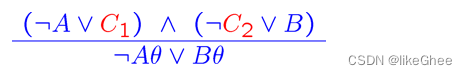
为了使C1和C2相同,需要统一
θ是为之统一的替换
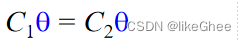
一个最通用的统一(MGU), 是统一替换θ(最多出现的字母)成θ’
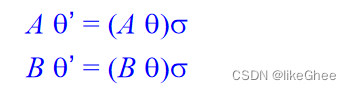
举个例子
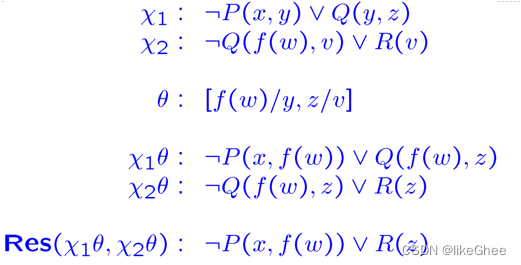
分解
C和A表示谓词公式,那么有
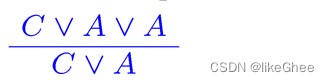
隐式分解的解析写法
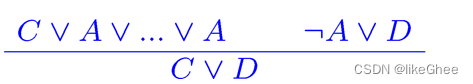
Unification Algorithm
统一算法公式

举个例子:
第一步找到对应相等的地方, 继续应用等号相同
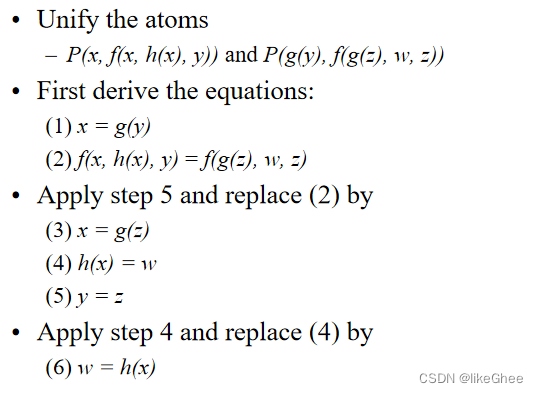
化简到最后,得到一组集合最简的等式, 继续替换最通用的字母,比如这里的x
继续替换最通用字符,到y
最后到最后不能再替换
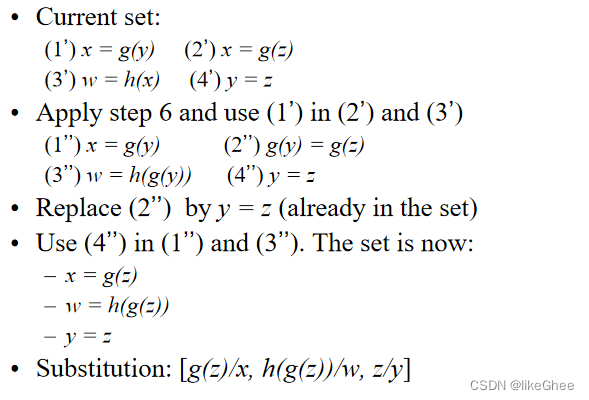
General Resolution
通用解析
考虑下面的一阶clauses
A,B,C,D都是原子命题
用θ表示Ak和Dl的mgu,然后resolution x1和x2
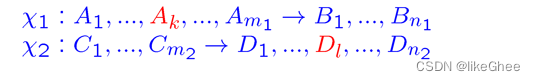
将Ak替换位Dl
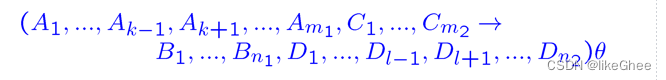
如果没有两个可统一的原子命题,那么resolution规则是未定义的(undefined)
例子,Example of General Resolution

S表示一系列的clauses
定义S0=S
假设Si已经被构造了
选择两个clauses x1,x2 ∈ Si
以定义Res(x1,x2) (解析 clause)
if Res(x1,x2) = □ , □表示空clause
那么原始的S(Original set)是unsatisfiable,不可满足的
否则,构造Si+1 = Si ∪ Res(x1,x2)
对所有可能的x1和x2,if Si+1=Si, 那么S是可满足的(satisfiable)
Soundness and Completeness of Resolution
完整性: 如果不满足的clause □通过resolution procedure产生,那么原始集合clause是不满足的
完备性: 如果一个clause集合是不满足的,那么空的clause □可以从resolution procedure中生成出来
Logic Programming
A logic program is a set of Horn clauses.
逻辑程序是一组Horn clauses
在逻辑程序设计中,不把clauses写成
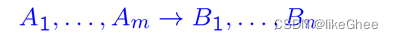
而是反过来
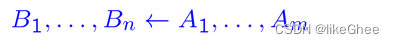
如果n=1,称为horn clause,逻辑程序是一组Horn clauses

H:head,A1,……,Am:body
如果n=0,则clause为目标goal
如果n=1,m=0,body为空,那我们得到了一个事实
如 B1 <-,则B1为一个事实
逻辑程序解析
解析过程加一些限制,可以提高计算效率。
计算规则是在goal clause 中选择literal
典型的计算规则:目标中最左边的原子。
搜索规则是一种用于选择clause的规则,用目标clause 中所选的literal进行解析。
典型的搜索规则:clauses按照编写的顺序进行搜索。
逻辑程序解析例子

Prolog程序最基本的形式是一组Horn clauses
给定一个目标,程序的执行和目标通过应用具有以下规则的解析过程来实现:
计算规则:在目标中从左到右选择literal
搜索规则:程序中从上到下选择clauses
用这些规则扩充的解析过程称为SLD-解析
Prolog语法
谓词和函数符号以小写字母开头
变量以大写字母或下划线开头
左箭头由:-操作符表示
点.充当子句分隔符
Example

程序的形式语义
只是一些简述
程序的形式语义
三种不同的风格
操作语义 Operational semantics
指定程序执行步骤
指称语义 Denotational semantics
一个程序被映射到一个值(程序的含义)
代数语义 Algebraic semantics
一组代数定律(方程/方程内)
弗洛伊德-霍尔逻辑Floyd-Hoare Logic 也被称为公理axiomatic语义
一些编程语法例子
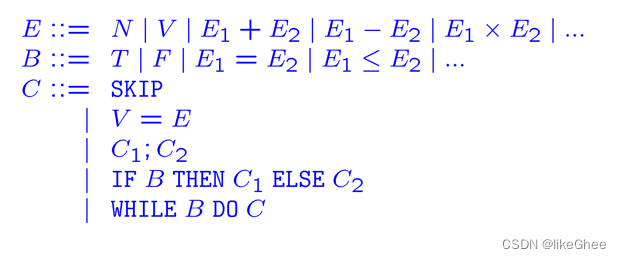
语义种类
整数Val ={…,-2,-1,0,1,2,…}
真值Bool = {tt, ff}
State状态
State = Var→Val
Lookup in a state: S X (or S(X))
更新状态
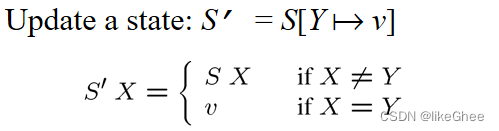
句法范畴的意义

算法表达式
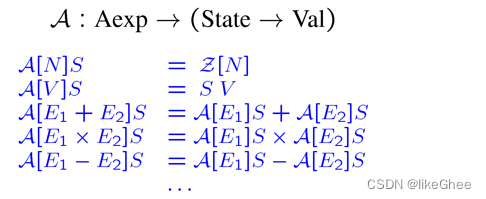
布尔表达式

Operational Semantics
操作语义
思想:用抽象的方法描述语句的执行效果,以免语义依赖于语言实现所用的具体计算机
步骤:
设计一个抽象机及其状态
定义每一个语句对状态的改变(或抽象机指令)
描述机器状态最简单的形式化模型:从合法名字集合到“值”的映射, 如,当x取值3,y取值5,z取值0时的状态为{x->3, y->5, z->0}

形式化定义: S : Name -> Value ∪ {⏊}
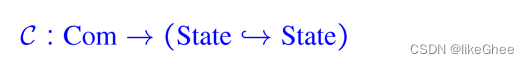
在操作方法中,我们感兴趣的是程序是如何执行的
我们将讨论由转换系统(transition systems)指定的结构操作语义(SOS)
Structural Operational Semantics (SOS)
SOS:描述计算的各个步骤是如何发生的
Transition System
定义几个符号

符号定义:
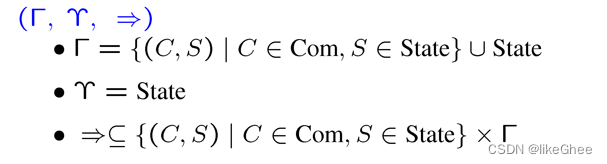
两种典型的transitions:
在一个计算步骤之后,计算还没有完成:
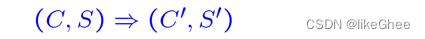
经过一个步骤的计算就完成了:

一些操作语义定义

Denotational Semantics
指称语义
基础:递归函数理论
思想:定义一个语义函数(指称函数),把程序的意义映射到某种意义清晰的数学对象 (就像用中文解释英文)
步骤:
为每个语言实体定义一个数学对象(语义域)
定义一个将语言实体的实例映射到该数学对象的实例的函数


操作语义用机器的状态来描述意义,指称语义用程序的状态来描述意义,在抽象层面上,这两者是一致的
关键区别:操作语义用某种编程语言编码的算法来定义状态变化,而指称语义用数学函数来定义最终效果,并不关心执行过程。
在指称方法中,我们感兴趣的是执行程序的效果
所谓效果,我们指的是初始态和最终态之间的联系
概念:语义功能
将每个语法构造映射到一个数学对象
特征:必须在成分上定义
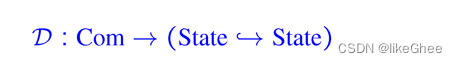
操作定义:

指称语义-关系模型
我们可以使用初始和最终状态之间的关系来指定程序执行的效果
一个关系:(αP, P)
给定一个程序P, X是它的变量。
它的语义用谓词P(X,X’)表示
其中X表示初始状态(执行前)下X的值,X '表示最终状态(执行后)下X的值。
Example
程序P: X = X+1
可能的观察集:{… , (1,2), (-2,-1),… }
我们可以使用谓词P: X ’ =X+1来表示集合,其中αP = {X}

Semantic Definitions
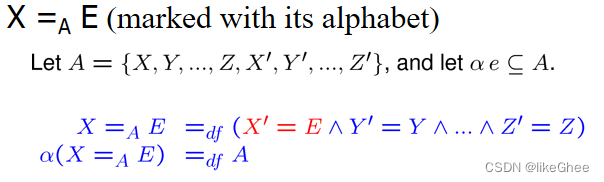
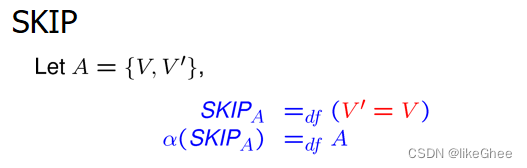
顺序组合

条件
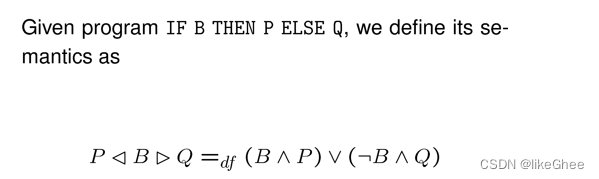
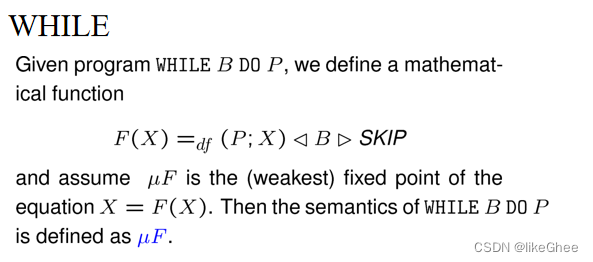
Algebraic Semantics
关于程序的代数定律
两个程序具有相同的语义(=)
或者一个程序比另一个好(⊑)
通常被认为是规则的集合
它可以用来把程序转换成正常的形式
可以用于编译、refinement等
Floyd-Hoare Logic
为了构造部分正确性规范的形式证明,需要公理和推理规则
这是Floyd Hoare Logic提供的
Floyd Hoare逻辑中的一个证明是a sequnce of line,每一条线要么是逻辑公理,要么遵循逻辑推理规则从更早的lines开始
现在我们将考虑程序规范和程序验证
Floyd-Hoare逻辑-程序逻辑
命令式程序的数学推理
它是机械化程序验证系统的基础
Hoare Notation
Hoare符号
程序是由赋值、条件等命令构建的
术语“程序”和“命令”是同义词, 前者只用于表示完整算法的命令
术语“语句statement”用于正确性规范中出现的程序变量的条件
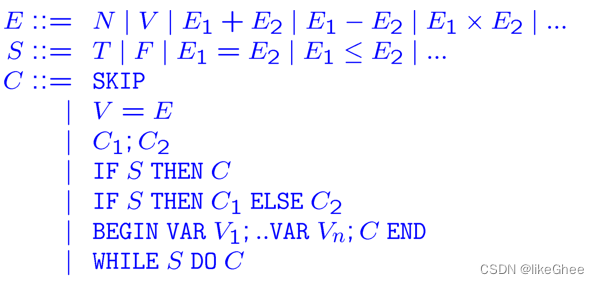
简述一下语法规范
符号V, V1,…, Vn表示任意变量
特定变量的例子有X、R、Q等
符号E, E1,…, En代表任意表达式(或术语)
比如X+1等,表示数值(通常是数字)
符号S, S1,…, Sn代表任意命题
如这些条件如X<Y, X=1等,不是真就是假
这些符号C, C1,…Cn代表编程语言的任意命令(commands)
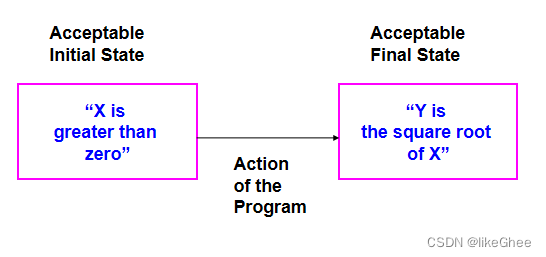
Program Specification 程序规范
命令式程序
执行命令式程序具有改变状态的效果
使用命令式程序
首先建立初始状态
设置一些变量
然后执行程序(将初始状态转换为最终状态)
然后检查最终状态下的变量值,以获得所需的结果
Floyd-Hoare Logic
Axioms and rules for Partial correctness
Hoare引入了以下表示法,称为部分正确性规范,用于指定程序的功能:
{P} C {Q}
C是一种来自编程语言的程序,它的程序被指定
P和Q是C中使用的程序变量的条件
程序变量的条件将使用标准的数学符号和逻辑运算符来编写

部分正确性规范
{P} C {Q} 称为 Partial correctness specification
P 是前条件
Q 是后条件
{P} C {Q} 为T:P条件开始执行程序C,如果C程序终止,结束状态满足Q
这是部分正确性是因为C程序执行不一定会终止
C不终止那么为T

Axioms and rules for Total correctness
完全正确性规范
[P] C [Q]
必须满足以P条件执行程序C,终止条件为Q才为T
完全正确=终止+部分正确
完全正确是最终目标,分开验证部分正确性和终止通常更容易
终止通常很容易显示,主要判断循环是否会死循环,但有时候会很难判断
例子:
引入辅助变量帮我们判断
{X=a ∧ Y=b} R=X; X=Y; Y=R {X=b ∧ Y=a}
执行这个程序会交换X和Y的值
变量a和b,它们不出现在命令中,用于命名程序变量X和Y的初始值
这里的a和b称为辅助变量或者ghost 变量
非正式的约定:
程序变量是大写的
辅助变量为小写
一些例子
{P} C {T}
这个规范适用于每个条件P和每个命令C,因为T总是为真
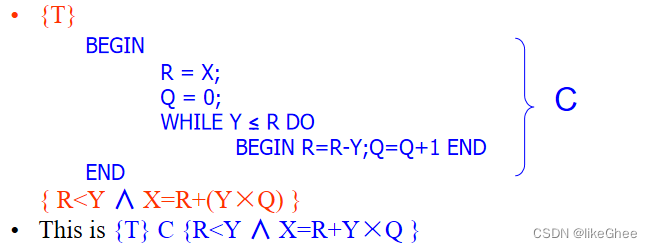
其中C是上面大括号表示的命令
如果每当C的执行停止时,Q是商,R是除Y除以X得到的余数,则规范为真
它是T的(即使X最初是负的)
例子:
程序必须将Y设置为X和Y的最大值
错误写法:[T] C [Y= max(X,Y)]
这里后置条件" Y = max(X,Y) “表示” Y是最终状态下X和Y的最大值"
正确写法:[X=a ∧ Y=b] C [Y = max (a, b)]
假设Csort是一个命令,用于对数组的前n个元素排序
为了正式规范说明这一点,设SORTED(A, n)表示 A(1)≤A(2)≤…≤A(n)
错误写法:{1≤N} Csort {SORTED(A, N)}
排序(A, N)可以通过简单地将A的前N个元素归零来实现
为了形式化,让PERM(A, A ‘, N)表示
A(1)、A(2)…,A(n)的重排是一个A’(1)A’(2),…,A’(n)
错误写法:{1≤N ∧ A=a} Csort {SORTED(A, N) ∧ PERM(A, a, N)}
Csort 将N设为1,则规范是正确的
正确写法:
{1 ≤ N ∧ A=a ∧ N=n}
Csort
{SORTED(A, N) ∧ PERM(A, a, N) ∧ N=n}
Proof Rules for Partial Correctness
这一节主要是小结和边角料,有点杂
形式证明明确了使用什么公理和推理规则来得出结论
对于那些实际上不合理的程序,很容易提出合理的推理规则
计算机程序的正确性证明通常非常复杂,需要正式的方法来确保其有效性
因此,必须充分明确所使用的推理原则,以便分析其合理性
下面的证明规则构成了我们编程语言的公理化语义(axiomatic semantics )

三种可能是真的或是假的东西
数学陈述,例如 X+1 = 1+X
部分正确性规范{P}C{Q}
总正确性规范 [P] C [Q]
算术定律提供了证明整数陈述的方法
逻辑系统提供了确定真相的规则(即证明各种判断)
Floyd Hoare逻辑提供了证明部分正确性规范的规则
⊦ S表示语句S可以被证明
如果S是语句,⊦ S表示S有证据,有证明的语句称为定理
Floyd Hoare Logic的公理由模式指定,这些可以被实例化以获得特定的 partial correctness specifications
Floyd Hoare Logic的推理规则将用以下形式的符号表示
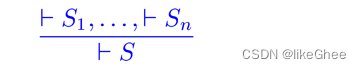
这些假设要么都是Floyd-Hoare逻辑的定理,要么是Floyd Hoare逻辑和数学定理的混合
语法:SKIP
语义:状态不变
SKIP公理
⊦ {P} SKIP {P}
P可以用任意谓词演算公式(语句)实例化
例子:
⊦ {Y=2} SKIP {Y=2}
⊦ {T} SKIP {T}
⊦ {R=X+Y×Q} SKIP {R=X+Y×Q}
语法:V=E
语义:将E的值赋给变量V来改变状态
Example: X = X+1
执行赋值后的变量V的值等于执行前状态下表达式E的值
如果在分配之后语句P为真,那么用E代替P中的V得到的语句在执行之前必须为真 P[E/V]
postcondition中的每个关于V的语句都必须对应于precondition中的一个关于E的语句
在初始状态下,V具有即将丢失的值
Assignment 公理
⊦ {P[E/V]} V = E {P}
其中V是任何变量,E是任何表达式,P是任何语句,符号P[E/V]表示用术语E替换语句P中变量V的所有出现的结果。
例子
⊦ {Y=2} X = 2 {Y=X}
⊦ {X+1=n+1} X = X+1 {X=n+1}
⊦ {E=E} X = E {X=E} (if X does not occur in E)
赋值的Backwards谬论
许多人认为赋值公理是“向后的”
一个常见的错误直觉是 ⊦ { P } V = E { P[V/E] },其中P[V/E]表示用V代替P中的E的结果
这是错误的,如⊦ {X=0} X=1 {X=0}
P: X=0
V:X, 1: E
P[V/E] => X 换 1,但是1不出现在(X=0)
另一个错误的直觉是⊦ { P } V = E { P[E/V] }
同样的例子:⊦ {X=0} X=1 {1=0}
P:X=0
V:X,E:1
P[E/V] : P中X换成1 => 1=0, 显然也是错误的
有效性
关于赋值公理很容易有错误的直觉,这一事实表明,有严格的方法来建立公理和规则的有效性是很重要的。
可以为我们的编程语言提供形式语义
然后证明Floyd Hoare逻辑的公理和推理规则是正确的
增加我们对公理和规则的信心,使我们相信形式语义的正确性
Blocks
Syntax: BEGIN VAR V1; … VAR Vn; C END
语义:执行命令C,然后将V1、…、Vn的值恢复为输入块之前的值
未指定块内V1、…、Vn的初始值
Example: BEGIN VAR R; R = X; X = Y; Y = R END
使用R作为临时变量交换X和Y的值
该命令对var R没有副作用
带有副作用的表达式
赋值公理的有效性取决于没有副作用的表达式
假设我们的语言被扩展到包含“块表达式” ,BEGIN Y = 1; 2 END,该表达式的值为2,但其求值也会通过在其中存储1而对变量Y产生“副作用”
如果赋值公理适用于块表达式,那么它可以用于推导
⊦ {Y=0} X = BEGIN Y = 1; 2 END {Y=0}
因为(Y=0)[E/X]=(Y=0),X未出现在(Y=0)
这显然是错误的,Y赋值了1
Sequences
Syntax: C1; …; Cn
语义:命令C1、…、Cn按该顺序执行
Example: R = X; X = Y; Y=R
使用R作为临时变量交换X和Y的值
该命令的副作用是将变量R的值更改为变量X的旧值
Precondition Strengthening
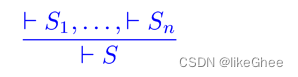
⊦S1,…,⊦Sn可以推出⊦S
使用此符号,前提条件强化规则为
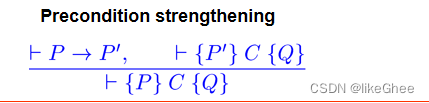
注意,这两种假设是不同的判断
eg1:
⊦ X=n → X+1=n+1
⊦ {X+1=n+1} X = X+1 {X=n+1}
前提强化
⊦ {X=n} X = X+1 {X=n+1}
其中n是辅助(ghost var)变量
eg2:
⊦ T → E=E
⊦ {E=E} X = E {X=E}
⊦ {T} X = E {X=E}
Postcondition Weakening
正如前面的规则是要加强部分正确性规范的前提条件一样,下面的规则允许我们削弱后条件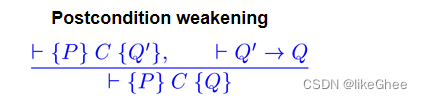
综合eg:
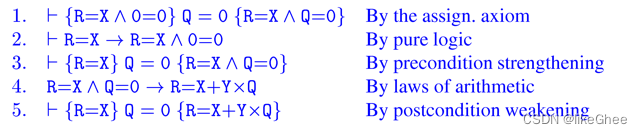
Precondition Strengthening和Postcondition Weakening规则有时被称为后果规则(rules of consequence
)
Sequencing Rule
规则实现了序列C1; C2的部分正确性规范
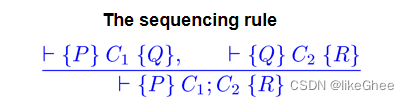
例子:
(1) ⊦ {X=x ∧ Y=y} R = X {R=x ∧ Y=y}
(2) ⊦ {R=x ∧ Y=y} X = Y {R=x ∧ X=y}
(3) ⊦ {R=x ∧ X=y} Y = R {Y=x ∧ X=y}
由(1)和(2),
(4) ⊦ {X=x ∧ Y=y} R = X; X = Y {R=x ∧ X=y}
由(4) and (3)
⊦ {X=x ∧ Y=y} R = X; X = Y; Y = R {Y=x ∧ X=y}
Block Rule

注意,块规则被视为包括没有局部变量的情况(“n=0”的情况)
Side Condition
Side Condition 边条件
没有变量V1、…、Vn出现在P或Q中的句法条件是边条件的一个例子
如果没有这个条件,规则是无效的,如下面的示例所示
⊦ {X=x ∧ Y=y} R = X; X = Y; Y=R {Y=x ∧ X=y}
⊦ {X=x ∧ Y=y} BEGIN VAR R; R = X; X = Y; Y=R END {Y=x ∧ X=y}
因为R没有出现在P和Q
⊦ {X=x ∧ Y=y} R = X; X = Y {R=x ∧ X=y}
不能推出
⊦ {X=x ∧ Y=y} BEGIN VAR R; R = X; X = Y END {R=x ∧ X=y}
因为R出现在Q
Conditionals Rule
Syntax: IF S THEN C1 ELSE C2
如果语句S在当前状态下为真,则执行C1
如果S为假,则执行C2。
Example: IF X<Y THEN MAX=Y ELSE MAX=X
var MAX的值被设置为X和Y的值的最大值。
One-armed conditional is defined by
IF S THEN C
F S THEN C ELSE SKIP

eg:
⊦ { T ∧ X < Y } MAX = Y { MAX = max(X, Y) }
⊦ { T ∧ ¬(X < Y) } MAX = X { MAX = max(X, Y) }
可以推得到:
⊦ {T} IF X < Y THEN MAX = Y ELSE MAX = X { MAX=max(X,Y) }
While Rule
Syntax: WHILE S DO C
如果语句S在当前状态下为真,则执行C并重复WHILE命令
如果S为假,则不执行任何操作
因此重复执行C直到S的值变为假,如果S永远不会变为假,那么命令的执行永远不会终止
Example: WHILE ¬(X=0) DO X = X-2
Invariants
⊦{P ∧ S} C {P}
当S成立时,P是C的不变量
WHILE规则规定
如果每当测试条件成立时,P是WHILE命令体的不变量,则P是整个WHILE命令的不变量
换句话说,如果执行C一次保留了P的真值,那么执行C任意次数也会保留P的真值
WHILE规则还表示这样一个事实,即WHILE命令终止后,测试必须为false,否则,它不会终止
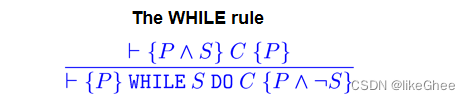
例子:
⊦ {X=R+Y×Q ∧ Y≤R} BEGIN R = R-Y; Q = Q+1 END {X=R+Y×Q}
因此,根据WHILE规则,令P=‘X=R+Y×Q’
⊦ {X=R+Y×Q}
WHILE Y≤R DO
BEGIN R = R-Y; Q = Q+1 END
{X=R+Y×Q ∧ ¬(Y ≤ R)}
我们可以很容易推导:
⊦ {T} R = X; Q = 0 {X=R+Y×Q}
因此,通过排序规则和后条件弱化
⊦ {T}
R = X;
Q = 0;
WHILE Y ≤ R DO
BEGIN R = R-Y; Q = Q+1 END
{ R<Y ∧ X=R+Y×Q }
Making Proofs Easier
先前我们知道了
用于指定程序执行的符号
证明其符合规范的方法
今天我们来看看寻找证据和组织证据的方法:
finding invariants
derived rules
backwards proofs
annotating programs prior to proof
然后,将展示如何自动化程序验证
finding invariants
如何找到不变量?
识别与循环相关的变量或变量
观察前n次迭代中这些变量的输出
从这些输出中引入不变量或解决这些输出上的约束
验证不变量的有效性;如果没有,请重新开始
分析事实:
最初必须成立
跳出循环时,它必须确定结果
每种东西必须保持不变
想想循环是如何工作的——不变量:
到目前为止做了什么
以及有待完成的工作
给出所需的结果
Example
{
X=n ∧ Y=1}
WHILE X != 0 DO
BEGIN Y = Y×X; X = X-1 END
{
X=0 ∧ Y=n!}
initially X=n and Y=1
finally X=0 and Y=n!
每次循环:Y增加而X减少
loop works:
Y持有迄今为止的结果
X!还有待计算
n!是期望的结果
=>
不变:X的减少与Y的增加相结合
The invariant is X!×Y=n!
另一个eg
{X=0 ∧ Y=1}
WHILE X<N DO
BEGIN X = X+1; Y = Y×X END
{Y=N!}
An invariant is Y=X!
最终需要Y=N!,但WHILE规则仅给出¬(X<N)
The invariant needed: Y=X! ∧ X≤N
At end: X≤N ∧ ¬(X<N) → X=N
通常需要加强不变量以使其发挥作用,
typical to add stuff to ‘carry along’ like X≤N
Conjunction and Disjunction Rule

这些规则对于将证明拆分为独立的bits很有用
证明⊦{P} C{Q1∧Q2}
通过分别证明
⊦{P} C{Q1}和⊦{P} C{Q2}
即可
理论上它们是多余的,但是,在实践中很有用
Derived Assignment Rule
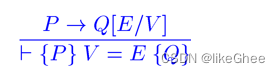
一个结合了两个步骤的规则
assignment axiom
precondition strengthening
我们如何知道这与Assignment Axiom一致?
它是否比分配公理更强大(即证明更强大)?
我们可以导出规则,而不是将其作为新的原语添加

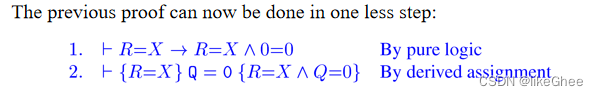
Rules for Consequence
与赋值示例中一样,所需的前置条件和后置条件很少采用原语规则所要求的形式
理想情况下,对于每个命令,我们都需要一个形式规则
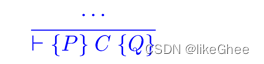
其中P和Q是不同的元变量。
有些规则已经采用这种形式,例如sequencing rule
我们可以使用后果规则为其他命令导出这种形式的规则
Derived Skip Rule
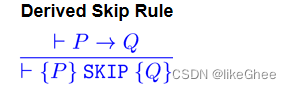
Derived While Rule

这源于While规则和后果法则
例子
⊦ R=X ∧ Q=0 → X=R+Y×Q
⊦ {X=R+Y×Q ∧ Y≤R} R = R-Y; Q = Q+1 {X=R+Y×Q}
⊦ X=R+Y×Q ∧ ¬(Y≤R) → X=R+Y×Q ∧ ¬(Y≤R)
Then
⊦ {
R=X ∧ Q=0 }
WHILE Y≤R DO
BEGIN R = R-Y; Q = Q+1 END
{
X=R+Y×Q ∧ ¬(Y≤R)}
Derived Sequencing Rule

(i) ⊦ {X=x ∧ Y=y} R = X {R=x ∧ Y=y}
(ii) ⊦ {R=x ∧ Y=y} X = Y {R=x ∧ X=y}
(iii) ⊦ {R=x ∧ X=y} Y = R {Y=x ∧ X=y}
直接推出
⊦ {X=x ∧ Y=y} R = X; X = Y; Y= R {Y=x ∧ X=y}
Derived Block Rule

(i) ⊦ {X=x ∧ Y=y} R = X {R=x ∧ Y=y}
(ii) ⊦ {R=x ∧ Y=y} X = Y {R=x ∧ X=y}
(iii) ⊦{R=x ∧ X=y} Y = R {Y=x ∧ X=y}
=>
⊦ {X=x ∧ Y=y}
BEGIN VAR R; R = X; X = Y; Y= R END
{Y=x ∧ X=y}
Sequenced Assignment
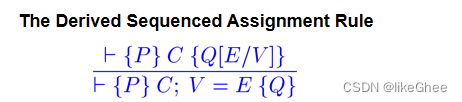
⊦ {X=x ∧ Y=y} R = X {R=x ∧ Y=y}
=>
⊦ {X=x ∧ Y=y} R = X; X = Y {R=x ∧ X=y}
Forward and Backward Proof
例如,为了证明⊦{P} C1;C2{Q}
首次证明⊦{P} C1{R}和⊦ {R} C2{Q}
然后推断⊦ {P} C1;C2{Q}排序规则
这种方法称为前向证明
通过规则从公理走向结论
前向证明的问题在于,要想达到你想要的目标,你需要证明什么并不总是容易的
倒行逆施更为自然
从{P}C{Q}的目标开始
生成子目标,直到问题解决
要证
{X=x ∧ Y=y} R = X; X = Y; Y= R {Y=x ∧ X=y}
子目标
{X=x ∧ Y=y} R = X; X = Y {R=x ∧ X=y}
子目标推导
{X=x ∧ Y=y} R = X {R=x ∧ Y=y}
这显然遵循赋值公理
前向证据说
我们已经证明了⊦ S1,我们可以推断⊦ S2
向后证明说
证明⊦ S2足以证明⊦ S1
通过向后证明证明了一个定理,提取向前证明是很简单的
例子:
To prove
⊦ {T}
R = X;
Q = 0;
WHILE Y≤R DO
BEGIN R = R-Y; Q = Q+1 END
{X=R+Y×Q ∧ R<Y}
By the sequencing rule, it is sufficient to prove
(i) ⊦ {T} R = X; Q = 0 {R=X ∧ Q=0}
(ii) ⊦ {R=X ∧ Q=0}
WHILE Y≤R DO
BEGIN R = R-Y; Q = Q+1 END
{X=R+Y×Q ∧ R<Y}
To prove (i), by the sequenced assignment axiom, we must prove
(iii) ⊦ {T} R = X {R=X ∧ 0=0}
To prove (iii), by the derived assignment rule, we must prove:
⊦ T → X=X ∧ 0=0
This is true by pure logic.
To prove (ii), by the derived while rule, we must prove:
(iv) ⊦ R=X ∧ Q=0 → (X=R+Y×Q)
(v) ⊦ X=R+Y×Q ∧ ¬(Y≤R) → (X=R+Y×Q ∧ R<Y)
(vi)⊦{X=R+Y×Q ∧ Y≤R} BEGIN R = R-Y; Q = Q+1 END {X=R+Y×Q}
(iv) and (v) are proved by arithmetic
To prove (vi), by the block rule, we must prove:
(vii) {X=R+Y×Q ∧ Y ≤ R} R = R-Y; Q = Q+1 {X=R+Y×Q}
To prove (vii), by the sequenced assignment rule, we must prove:
(viii) {X=R+Y×Q ∧ Y ≤ R} R = R-Y {X=R+Y×(Q+1)}
To prove (viii), by the derived assignment rule, we must prove:
(ix) X=R+Y×Q ∧ Y ≤ R → X=R-Y+Y×(Q+1)
This is true by arithmetic.
注释
排序规则引入了一个新的语句R

要应用此规则,需要提出一个合适的语句R
如果第二个命令是赋值,则可以使用顺序赋值规则,然后有效地填充值
同样,要使用派生的While规则,我们必须发明一个不变量。
在开始证明并用它们注释程序之前,思考这些陈述是很有帮助的
当你需要证据时,这些信息就可用了
这可以帮助你避免陷入细节
每当控件到达该点时,注释应为true
例如,以下程序可以在指定的点处进行注释。
⊦ {T}
R = X;
Q = 0; {R=X ∧ Q=0} ← P1
WHILE Y ≤ R DO {X=R+Y×Q } ← P2
BEGIN R = R-Y; Q = Q+1 END
{X=R+Y×Q ∧ R<Y}
Mechanising Program Verification
机械化程序验证将描述一个简单程序验证器的架构
根据Floyd Hoare Logic的规则
很明显即使正在验证的程序很简单,证明也很长,很枯燥
许多棘手的小细节需要处理,其中许多都是微不足道的,例如。
⊦ (R=X∧ Q=0)→ (X=R+Y X Q)
目标:在Floyd Hoare逻辑中自动生成形式证明的例程
不幸的是,逻辑学家已经表明,原则上不可能设计一个决策程序来自动决定任意数学陈述的真假
一般决策程序的不存在仅仅表明人们不可能希望自动证明一切
在实践中,很有可能建立一个将验证的枯燥和常规方面机械化的系统

输入:用数学语句注释的部分正确性规范
这些注释描述了变量之间的关系
系统生成一组称为验证条件(VC)的纯数学语句
如果验证条件是可证明的,那么原始规范可以从Floyd Hoare逻辑的公理和规则中推导出来
验证条件被传递给定理证明程序,该程序试图自动证明它们
如果失败,将向用户寻求建议
Verification conditions
用verifier证明Hoare {P}C{Q}的三个步骤
1 通过在程序C中插入语句(称为断言)来对程序C进行注释,这些语句表示要在各个中间点保持的条件,这一步很棘手,需要对程序工作原理的充分理解,自动化是一个人工智能问题
2 然后根据注释的规范生成一组称为验证条件(简称VC)的逻辑语句
这完全是机械的,很容易由程序完成
3 验证条件得到证明
需要自动定理证明(即更多的人工智能)
为了改进自动验证,可以尝试
减少所需注释的数量和复杂性
提高定理证明器的能力
仍然是一个非常活跃的研究领域
验证条件的有效性
可以看出
如果能够证明
{P}C{Q}
then
⊦ {P}C{Q}
步骤2将验证问题转换为常规数学问题
该过程将通过以下内容进行说明:
⊦ {T}
R = X;
Q = 0;
WHILE Y≤R DO
BEGIN R = R-Y; Q = Q+1 END
{X=R+Y×Q ∧ R<Y}
步骤1是插入注释P1和P2
⊦ {T}
R = X;
Q = 0; {R=X ∧ Q=0} ← P1
WHILE Y≤R DO {X=R+Y×Q } ← P2
BEGIN R = R-Y; Q = Q+1 END
{X=R+Y×Q ∧ R<Y}
注释P1和P2表示每当控制到达它们时要保持的条件
控制仅到达P1放置一次的点
每次执行WHILE主体时,它达到P2, P2是WHILE命令的不变量
每当发生这种情况时,X=R+Y×Q成立,即使R和Q的值不同
步骤2将生成以下四个验证条件
T → (X=X ∧ 0=0)
(R=X ∧ Q=0) → X=R+Y×Q
X=R+Y×Q ∧ Y≤R → X=R-Y+Y×(Q+1)
X=R+Y×Q ∧ ¬(Y ≤ R) → (X=R+Y×Q ∧ R<Y)
步骤3包括证明四个验证条件
易于使用现代自动定理证明器
Annotation of Commands
带注释的命令是一个内嵌有statements (assertions)的命令
如果在以下位置插入了语句,则会正确注释命令
(i) 在 not an assignment command C1、C2、…、Cn中的每个命令Ci(其中i>1)之前
(ii)WHILE(和FOR)命令中单词DO之后
插入的断言应该表示每当控制到达断言发生的点时期望保持的条件
Annotation of Specifications
正确注释的规范是规范{P}C{Q},其中C是正确注释的命令
例子:为了正确注释,断言应该位于下面规范的第1点和第2点
⊦ {X=n}
BEGIN
Y = 1; ← 1
WHILE X != 0 DO ← 2
BEGIN Y = Y×X; X = X-1 END
END
{X=0 ∧ Y=n!}
合适的陈述如下
at 1: {Y=1 ∧ X=n}
at 2: {Y×X!=n!}
Verification Condition Generation
根据注释规范 {P}C{Q} 生成的验证条件,考虑C的各种可能性来描述验证条件
我们将使用以下形式的规则逐个命令地描述它:
The VCs for C(C1,C2) are
vc1 … vcn
together with the VCs for C1 and those for C2
每个VC规则将对应于逻辑的原语或派生规则
VC生成程序
生成验证条件的算法是基于命令结构的递归算法
刚才给出的规则对应于递归程序子句:
VC(C(C1,C2) ) = [vc1 … vcn] @ (VC C1) @ (VC C2)
选择这些规则,以便在每种情况下仅应用一个VC规则
应用它们完全是机械的
选择基于语法
每种情况下只有一条规则适用,因此VC生成是确定性的