Frenet坐标系下横纵向轨迹决策规划（SL投影及ST投影）及Apollo决策算法解析

参考：

（1）《攻城狮说 | 应对复杂路况，自动驾驶如何规划它的下一步？ “老司机”炼成记！》微信公众号文章 Pony.ai小马智行 

（2）《【Apollo】apollo3.5决策分享 --by 百度美研 Yifei Jiang老师》知乎

（3）《Baidu Apollo代码解析之s-t图的创建与采样（path_time_graph)》 CSDN

（4）《技术文档 | 二次规划（QP）样条路径》微信公众号文章 Apollo开发者社区 

（5）《开发者说｜Apollo5.5 规划算法解析》 知乎

（6）《自动驾驶之轨迹规划6——Apollo EM Motion Planner》CSDN

一、何谓轨迹规划

Apollo的 Planning 分为参考线平滑、决策、路径规划、速度规划等部分。

从整体上来说，规划模块的架构分为两个部分：一部分负责对数据的监听、获取和预处理；另一部分负责管理各个优化模块。数据进入后，对其综合处理为规划模块的内部数据结构，由任务管理器调度合适的优化器进行各个优化任务。综合优化的结果，经过最终的验证后，输出给控制模块。

扫描二维码关注公众号，回复： 14753945 查看本文章

1.1 轨迹规划的概念

       自动驾驶轨迹规划的核心就是要解决车辆该怎么走的问题。一辆自动驾驶车辆处在周围有行人、骑自行车的人以及前方有卡车的环境下，现在它需要左转，该怎么做？这就是轨迹规划该解决的问题。

         轨迹规划的输入包括拓扑地图、障碍物及障碍物的预测轨迹、交通信号灯的状态，还有定位、导航（因为知道目的地才能规划路径）、车辆状态等其他信息。而轨迹规划的输出则是一个轨迹，轨迹是一个时间到位置的函数，也就是特定的时刻要求车辆在特定的位置上。上图中轨迹函数是t→(x,y,z)，把 z 标灰是因为目前为止我们的车还不会飞，所以z是(x, y)的函数。

1.2 非凸优化问题

      轨迹规划本质上来说是一个优化问题。谈到优化问题，我们往往需要知道优化的约束和优化的目标。

      首先看轨迹规划的约束，第一个约束就是车辆要遵守交规，这是强制性的约束；第二个约束是要避免碰撞；第三个约束是要使规划的轨迹在车辆控制上可实现，例如不能出现规划出一条车根本拐不过来的急弯的轨迹。

       而优化的目标是使得自动驾驶跟人类司机驾驶相似，具体表现就是乘客乘坐时感到舒适。但“开得像人”也有不同的优化目标，比如我们可以驾驶得稳一点也可以开得急一点，像老司机一般。

       这样一个优化问题在数学上的性质是什么呢？数学上，解决一个优化问题，首先看这个优化问题是不是凸的，因为凸的问题比较好解一些。

       什么是凸优化问题？可以简单描述为，一个问题如果有两个可行解，则要满足这两个可行解的线性组合也是可行的，且不比这两个可行解都差。

       那么轨迹规划是不是一个凸优化问题呢？可以拆解来看，我们求解轨迹规划的t→(x,y)问题时，发现其复杂度较高且计算量较大。所以常见的解法是把轨迹规划分成横向规划和纵向规划。可以把这两个子问题看成t→(x,y)在空间上的投影，只要二者之一不是凸的，则轨迹规划问题就不会是凸的。

       横向规划，即s→(x,y)，决定了轨迹的形状，纵向规划是t→s，是指在此形状上运动的速度状态，也就是时间与位移的关系。横向规划和纵向规划联合起来就是t→(x,y)。

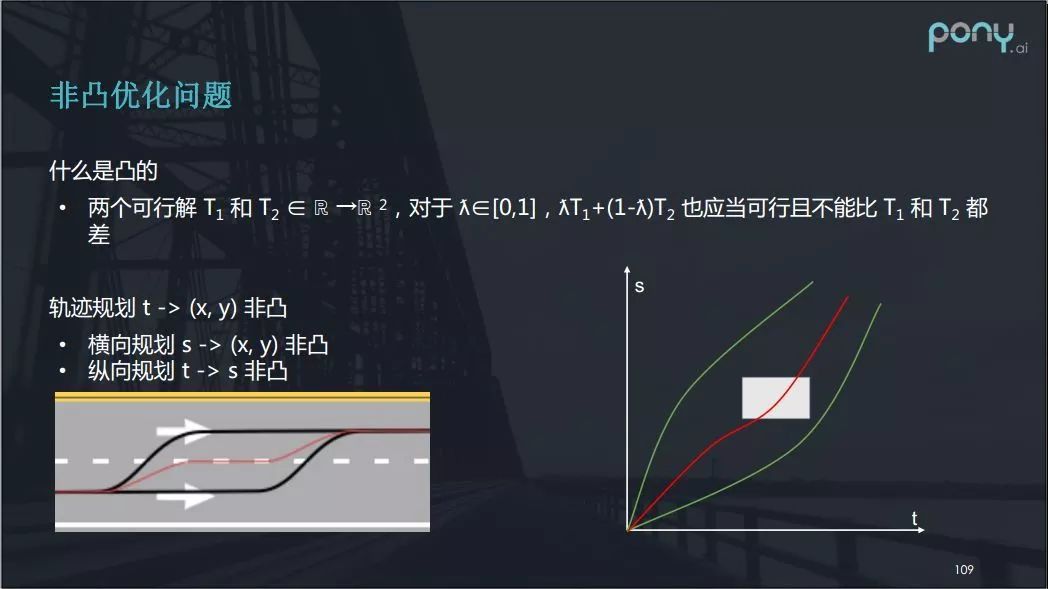
       那么横向规划是凸优化问题吗？如上图中的左侧图，没有显示时间信息，这就是横向规划。两条黑线代表不同的变道轨迹都是可行解，然后我们看其线性组合也就是中间的红线，这条红线的变道轨迹明显是不能用的——它变道太慢，骑线行驶距离过长。所以，根据数学定义，横向规划是非凸优化问题。

       再来看看纵向规划。纵向规划常以上图右侧的 t - s图 表示，t 表示时间，s 表示我们走过的路程。当一个行人横穿马路时，我们可以用白色矩形在t - s图上表示此过程，左边界表示行人进入规划路径（考虑车宽）的时刻，右边界表示离开规划路径的时刻。横轴上的上下边界差可以理解为行人占用的规划路径的宽度。

       面对这样场景，纵向规划将有两种选择，一种是车要让人，对应图中白色矩形下方的绿色路线；一种是车辆加速超过，即上方的绿色路线。但它的线性组合可能是图中的红线，而这条路线中行人与车已经撞上，显然是不可行的路线（解）。所以纵向规划也不是一个凸的问题。

二、基于场景选择的决策模块

       决 策 模 块  相当于无人驾驶系统的大脑，保障无人车的行车安全，同时也要理解和遵守交通规 则。 为了实现这样的功能，决策模块为无人车提供了各种的限制信息包括：1) 路径的长度以及左右边界限制；2) 路径上的速度限制；3) 时间上的位置限制。

        此外，决策模块几乎利用了所有和无人驾驶相关的环境信息，包括: 1) Routing 信息；2) 道路结构，比如当前车道，相邻车道，汇入车道，路口等信息； 3) 交通信号和标示，比如红绿灯，人行横道，Stop Sign，Keep Clear 等； 4) 障碍物状态信息，比如障碍物类型，大小，和速度；5) 障碍物预测信息，比如障碍物未来可能的运动轨迹。

       正是因为决策模块处理了所有上层业务逻辑信息，并输出了抽象的限制信息，我们保证了下 游路径和速度优化的抽象性，并完全和上层的地图，感知，预测的解耦。

2.1 为什么需要决策模块？

       答案： 决策使轨迹规划化繁为简。既然轨迹规划是非凸优化问题，我们需要利用决策模块来解决这个问题。

       什么是自动驾驶的决策模块呢？从数学上来讲，决策就是为了限定非凸问题（轨迹规划）的解空间，将问题转化为凸的。

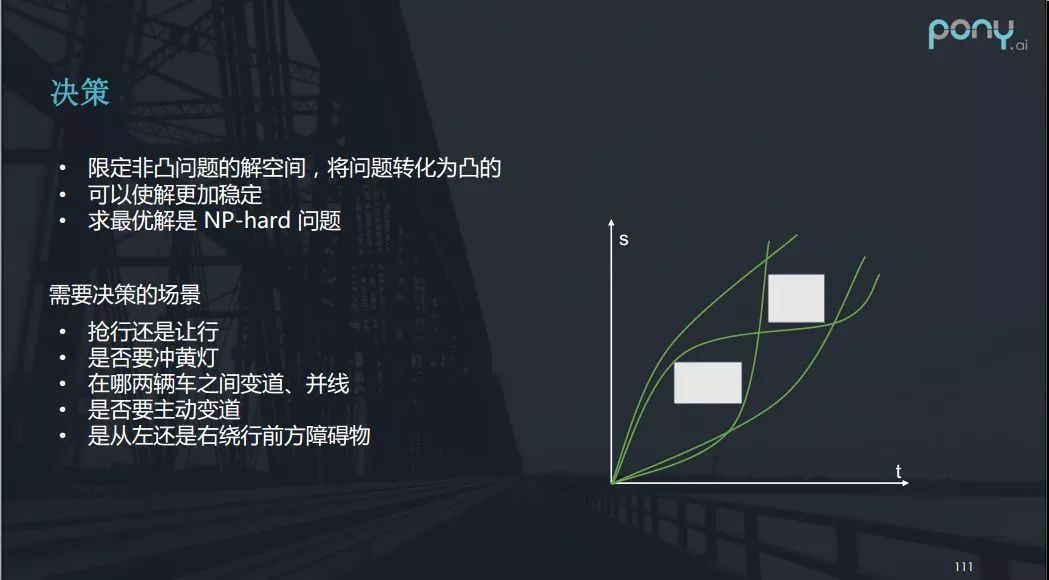
       我们可以看上图的例子：两个行人正在横穿马路，自动驾驶大体上可以作出四种不同的决策，即让两个人；超两个人；让一超一；超一让一。

       而一旦决策确定，那么路径规划就可转换为凸的问题，求解就会相对来说比较容易，也会使解更加稳定。因为一个单纯的数值优化问题的求解，很难保证每一帧的解都是相对稳定的，甚至可能出现第一帧要让，而第二帧却要冲的问题，决策可以提前规避这种不稳定。

       我们需要注意，决策是一个NP-hard（非确定性多项式困难）问题。自动驾驶需要决策的场景涉及许多，包括抢行还是让行，是否要冲黄灯，在哪两辆车之间变道、并线，是否要主动变道，是从左还是右绕行前方障碍物。只有做了决策才能使轨迹规划问题变为凸优化问题。

       处理凸问题可以利用的快速算法有许多，线性规划、二次规划、序列二次规划……，这些都是数值求解优化问题的方式。例如在二次规划中，如果Q正定，二次规划就是凸的问题，求解它会更加迅速和容易。

2.2 纵向规划决策求解：动态规划

       在纵向规划决策上，我想介绍一种以动态规划算法作为决策的方法。

       看看下图的案例，假设有两个人正在横穿马路，我们来研究一下如何决策才是最优的选择。

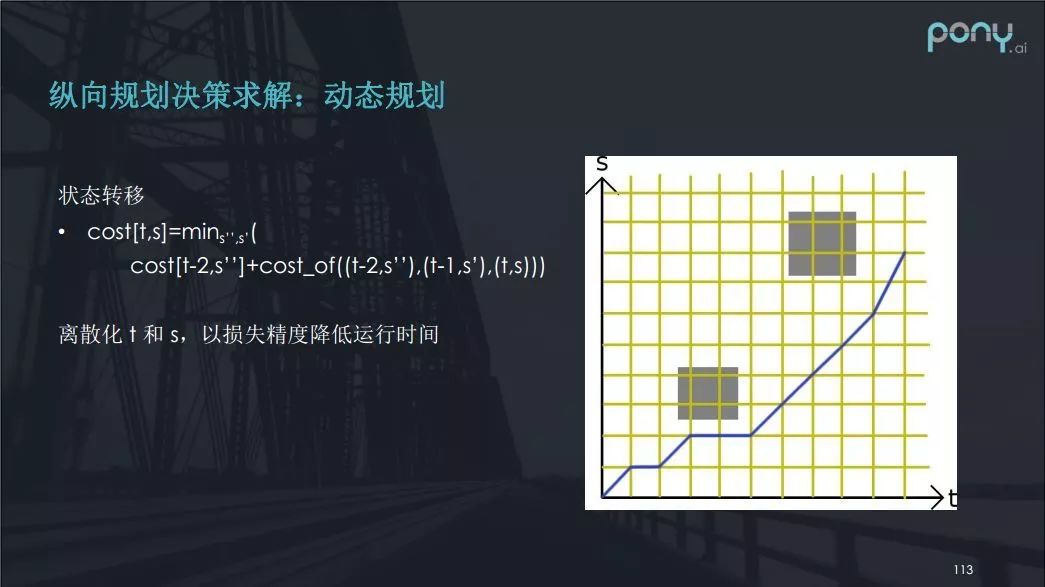
       首先，将 t - s 图进行离散化，离散化之后，我们可以认为每一步的决策只与前边的两步有关系。两步是因为我们可以近似求出加速度，并能写出一个状态转移方程。

       尽管这个方程在实际过程中比较难写，但确实是一种做法。虽然离散化 t 和 s 降低了精度，但降低精度也帮助降低了运行时间。

       注意，这种方法并不能保证最后的速度是否舒适，它给出的是一个大概的决策方法，即到底让或者不让。

2.3 决策面临的挑战

       第一个挑战上面已经提到，由于决策问题是一个NP-hard问题，不易直接求解，存在多种多样的近似算法。

       第二个挑战是很难用规则去拟合人的经验，包括上述的状态转移方程中的cost也很难去表示。目前解决这个挑战可用的部分办法是根据各种不同的情况建立数学模型，以及采用机器学习的方法进行决策。

       以上图左侧的场景为例，一辆正在行驶的自动驾驶车辆打算绕行前面白车，但此时前车突然起步了，我们该如何继续行驶？是变道？还是跟在后边行驶，又或是继续绕行？处理这种情况确实依靠人类驾驶的经验。再看上图右侧的例子：自动驾驶车准备在前方左转，但是前车停了很久也没有启动（可能前车驾驶员没反应过来），我们这时该不该变道呢？对这种情况，人类司机有时也很难判断。由此可见，场景的多变而复杂使得决策面临很多挑战。

2.3 Apollo3.5中分场景决策规划

       关于“场景”的概念是在 Apollo3.5 中首次提出，一个场景既可以是地图中的一个静态路段， 比如十字路口；也可以是无人车想要完成的一个动态目标，比如借道避让(Side Pass)。 依据场景来做决策和规划有以下两个优点：1)场景之间互不干扰，有利于并行开发和独立调参； 2)在一个场景里我们可以实现一系列的有时序或者依赖关系的复杂任务。

       这样的场景架构也有利于开发者贡献自己的特有场景，并不影响其他开发者需要的功能。 同时场景架构也带来了一些难点: 首先，场景的通用部分会带来代码的冗余，不便于代码的升级维护；其次，场景的划分，尤其是保证场景之间没有功能上的覆盖也很困难； 最后，有了多个场景之后，需要额外的逻辑来进行场景识别以及处理场景之间的转换。

        场景的划分其实没有特别严格的规定，同时这也取决于自动驾驶的应用场景，比如送货小车 和高速卡车在场景的划分上肯定不太一样。上图中，给出了 Apollo 场景分类的一个例子， 来尽量保证每个场景之间相对独立 我们把场景分为两大类，Lane Follow 和 Lane Breaking: Lane Follow 场景下主车沿一条车道驾驶，该车道前方一定距离内没有其他车道与其交汇或 者穿越;并且主车也没有切换到其他车道的意图。非 Lane follow 的其他场景被分类为 Lane Breaking。 在 Lane Breaking 下，我们又细分为三个小类: Intersection 是所有的路口场景; Active Pass 包括了所有临时借道的场景; Lane Switch 包括了所有换道的场景(包括车道合并)。

       有了场景的分类之后，我们就可以对场景进行识别和转换。对于选择哪个场景，我们采用了 两层的识别机制。 首先，每一个场景自己会根据当前的环境信息，确定是否属于自己的场景，并返回该信息给 场景管理器，场景管理器再统一进行选择，以保证场景的选择最优。 场景的退出也由每个场景自己决定，比如场景运行完成或者内部出错。一旦进入一个场景， 该场景会有较高优先级来完成。

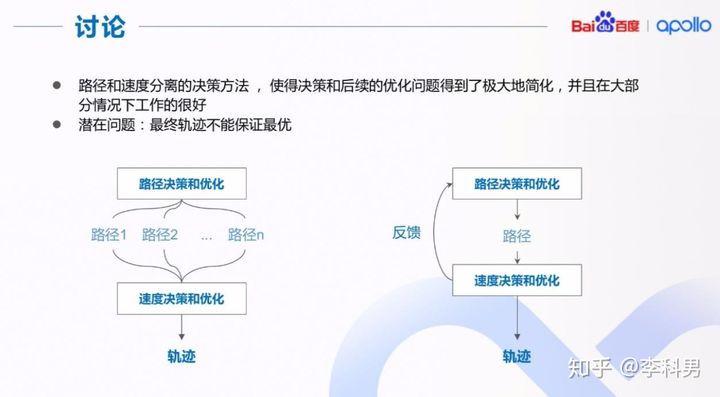
       用借道避让场景的一个实现，来说明场景是如何实现的。 在这个场景中，我们有 6 个 Stage(阶段)，每个 Stage 完成借道避让的一个步骤，类似于有 限状态机中的一个状态。主要步骤/状态有一定的时序依赖关系，如果在一个 Stage(阶段) 中发现环境变化了，或者出现错误，会出现 Stage 之间的跳转或者退出该场景。

       在每一个 Stage(阶段)中，都要实现上图中的功能，包括交规决策、路径决策、路径优化、 速度决策、速度优化。 我们把每个功能定义为一个或者几个基本的 Task(任务)，每个 Stage(阶段)或者直接调 用(使用默认参数)，或者修改参数，或者修改输入值。这样的实现可以极大的提高场景之 间的代码复用。

三、横纵向轨迹规划

3.1 横向规划

（1）横向规划的解法

       前面提到轨迹规划可以拆成横向和纵向的规划，现在我来具体介绍横向规划的解法。横向规划就是行车方向上的规划，可以看成是如何打方向盘的规划，它决定了轨迹的形状。

       这个问题通常的解法分两种，一种是无车道的场景，比如在freespace（自由空间）中规划或者泊车之类的场景，车辆一般处在低速行驶状态，缺乏车道线等先验信息。业界大多都用搜索等路径生成的方式去处理无车道场景。

       另一种是有车道的情况。虽然可以参考车道线信息，但是规划上想输出s→(x,y)函数，难度并不小。常见的做法是离线生成参考线，随后就可以将求解s→(x,y)的问题变为求解s→l的问题，l是指车辆在这个参考线上的横向偏移量。

       以上图右侧场景为例，原本车是沿车道向前走，但由于有前方车辆的遮挡，我们就必须绕行它，即向右横向偏移。

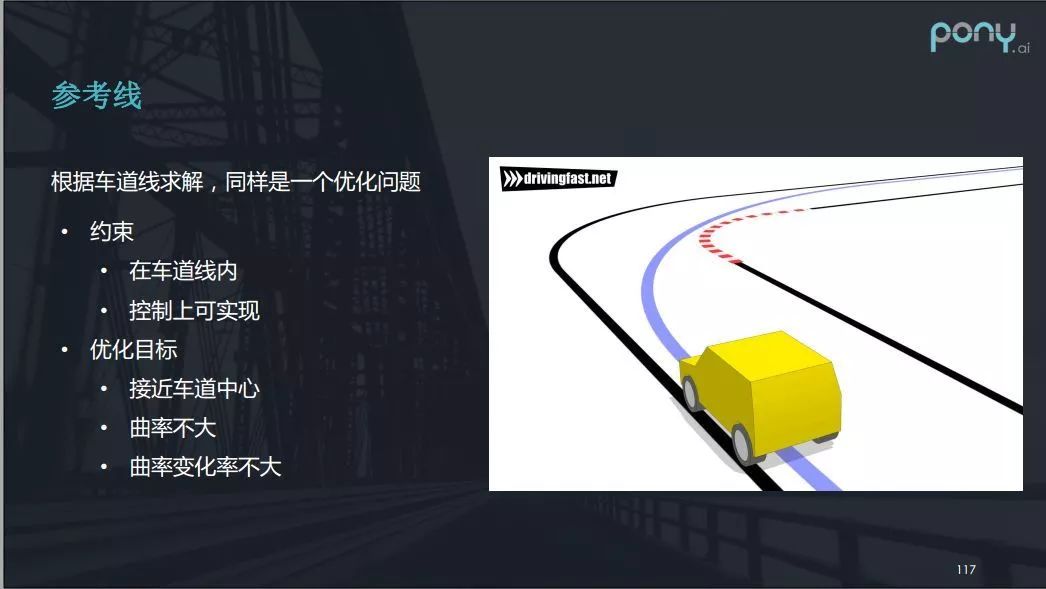
       而参考线的生成，其实类似于开卡丁车时别人教你的过弯的最优路线，它也是一个优化问题，当然也要保证安全性和舒适性。方便的是，有了高精地图辅助后，参考线可以通过离线去进行，所以可以用一些开销比较大的算法做到最优。参考线的约束在于其需要在车道线内，并且在控制上可实现。优化目标则是参考线需接近车道中心，曲率不能太大，曲率变化率也不大。

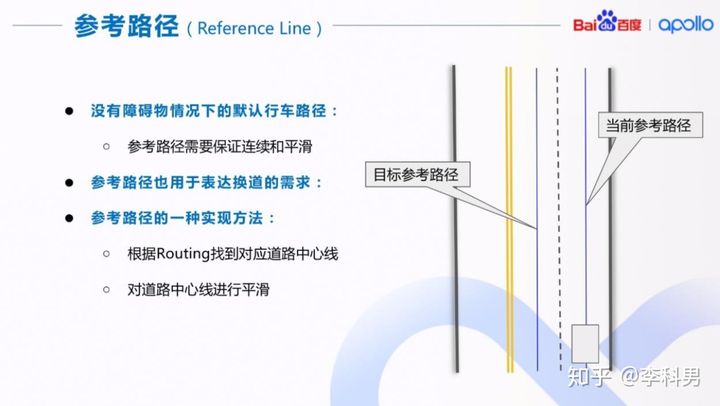
参考路径(Reference Line) 在 Apollo 决策中起着非常重要和关键的作用。 首先，参考路径是在没有障碍物路况下的默认行车路径。 其次，后续的交规决策，路径决策，和速度决策都是基于参考路径或者参考路径下的 Frenet Frame 完成的。 最后，参考路径也用于表达换道的需求，一般换道时会有两条参考路径，分别有不同的优先级。其中，优先级高的路径表示目标路径，优先级低的路径为当前路径(如图所示)。参考路径的获取可以有多种方式。 在 Apollo 里，参考路径的计算是根据 routing 的线路，找到相应的高精地图中的道路中心线，然后进行平滑。 有了参考路径之后，我们会沿着该路径找到所有在该路径上的交通标示和交通信号灯，并根据一系列的交通规则来决定是否在需要停止在交通标示或者交通信号灯的停止线前。

       确定参考线后，通过把参考线离散化，采一些点出来，那么横向规划问题就转化为求解一个离参考线偏移距离的一个问题，即转化成s→l的问题。其约束是车辆行驶不跨越边界，避免碰撞，而优化的目标是要离参考线近，要离障碍物远，曲率不大，曲率变化率不大等等。

       借助上图右侧的例子，你会发现横向规划可看成一个二次规划（QP）的问题。其中“0”，“-1”，“-2”是自动驾驶车行驶过的路径，0号点是车当前的位置，现在我们需要解的就是1，2，3，4，5，6这些点相对于参考线的横向偏移x。换句话说，已知x[-2]，x[-1]，x[0]，求解x[1]，x[2]等。该函数约束是车辆行驶不能超过左右边界包括马路牙，实线，障碍物等。优化目标则是车辆要离参考线近，方向盘不能打太多太快，保证乘坐的舒适。上图中的公式其实是一个关于x的二次的形式，所以可以使用二次规划的方法来解决。

（2）横向规划的挑战

       虽然大部分时候车都行驶在有车道线的马路上，但也会面临特殊的挑战。例如下图里左侧显示的路口，我们的车行驶的方向上有三条直行车道，但过路口后变成四条直行车道，并且对得很不齐。现实中，右侧的行驶的车（白车）往往不依据车道线行驶，可能会横跨车道线挤占自动驾驶车辆所在车道的空间。

       而下图右上角则展示了没有车道线的主辅路场景。在这种主辅路之间切换，就像解决一种没有参考线的freespace的规划，挑战也不小。总的来说，要想解决没有车道线或者说普通车辆不按车道线行驶的路径规划问题，难度都不小。

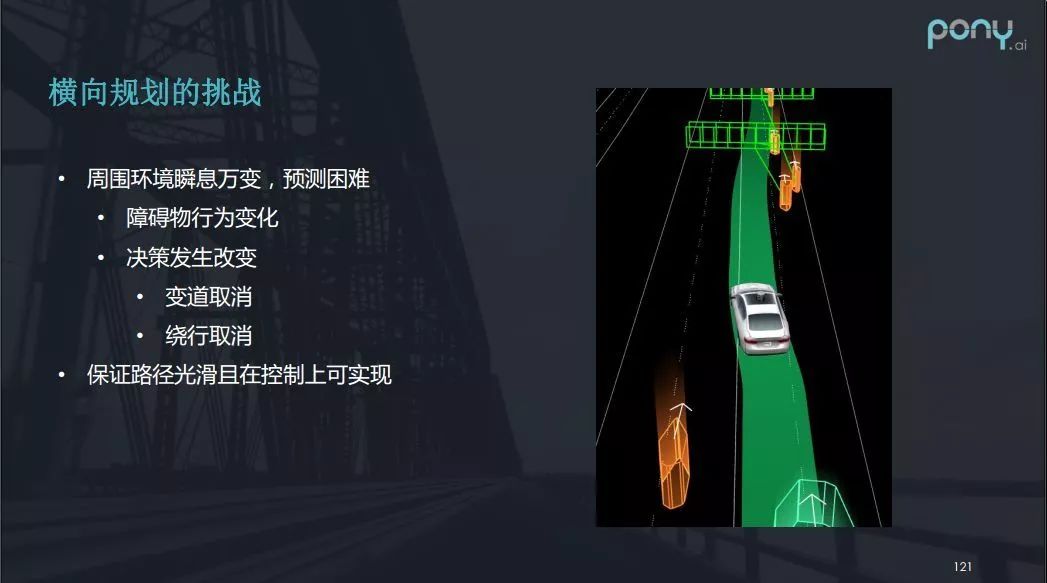
       另外的挑战就是环境的问题，因为车外行驶环境瞬息万变，要对周围进行环境预测也很困难。以下图为例，我们的自动驾驶车准备往左变道，而左下角橙色块代表的摩托车正飞速地向前行驶，于是我们的车辆迅速给出取消变道的决策，生成平滑的曲线回到原来行驶的道路上。因此，面对这类的情况，轨迹规划模块需要保证规划的路径光滑且在控制上可实现。

3.2 纵向规划

（1）纵向规划的定义和场景（常见的ST图）

       纵向规划本质是对车辆在设定好的路径上的速度规划，决定了车辆在整个轨迹上的运动过程。求解这类优化问题，第一个约束是遵守交规（信号灯、限速、停车让行等），第二个约束是避免碰撞。而纵向规划的优化的目标是乘坐舒适，也意味着车辆的速度变化率不大，加速度变化率不大，行驶速度也要尽量快一点（限速内）等。

       前边我提到了行人横穿马路的场景，在 t - s 图中，行人的运动过程可以转化一个矩形，最终给出了两种车辆的对应决策——加速超过行人或减速让行。那么决策之后该怎么做呢？

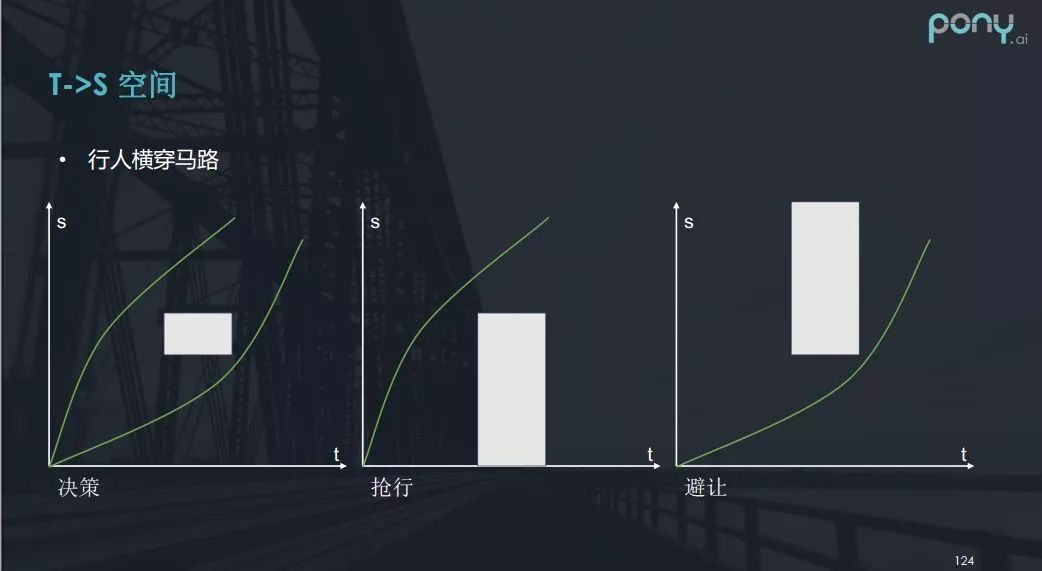
       如果决定要抢行，我们可以将矩形的约束条件扩展到最下部，便能转化为凸问题求最优解。如果采取避让，车辆的路线则从t - s图中的矩形下边穿过。

       但是如果是行人斜着穿过马路呢？在t - s 图中，行人的运动过程又该如何表示？答案就是一个斜向上的平行四边形（如上图）。

       黄灯也是我们要应对的场景之一。黄灯即将到来，如果决策要冲，那么车辆须尽快通过路口，否则很容易被逼停在路中间出不去。

        这种情况我们也可以用一样的 t - s 图表示（上图），左边界是表示黄灯亮的时刻，这个白色矩形存在一个缺角。当黄灯亮起的时候，车辆如果要尽快通过路口，那么随着t在增大的过程中，s也要迅速增大，并且增大的速率要超过缺角的斜率。

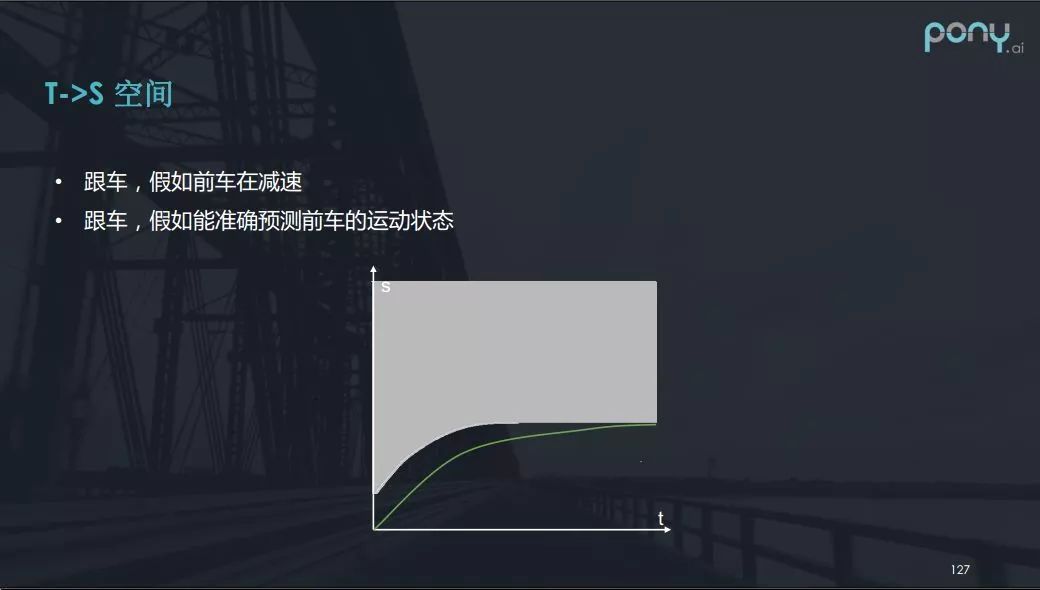
        再看一些更有趣的场景案例（上图）。当自动驾驶车跟车时，假设所跟的前车在减速，如果能够精确预测前车的运动的状态，那么展现在t - s图中的白色部分会出现各种各样的形状，这样解优化问题就能解出一条好的速度曲线。

（2）Apollo中基于ST图的纵向（速度）规划

       有了路径边界后，我们调用路径优化器(Path Optimizer)得到在边界限制内的平滑路径。 得到平滑的路径后，我们就可以在路径上进行速度决策。速度决策的流程如上图所示。

       我们首先对一整条路径或者部分路径产生一个或者多个速度限制边界(Path Bounds)，然后对多个速度边界进行集成，得到最终的路径上的速度限制边界( Speed Bound Overs )。 得到速度限制之后，我们在利用 ST 图来得到时间上的位置限制边界( Position Bound Over t )。最后我们把速度边界和位置边界传给速度优化器(Speed Optimizer)得到平滑的速度规划。

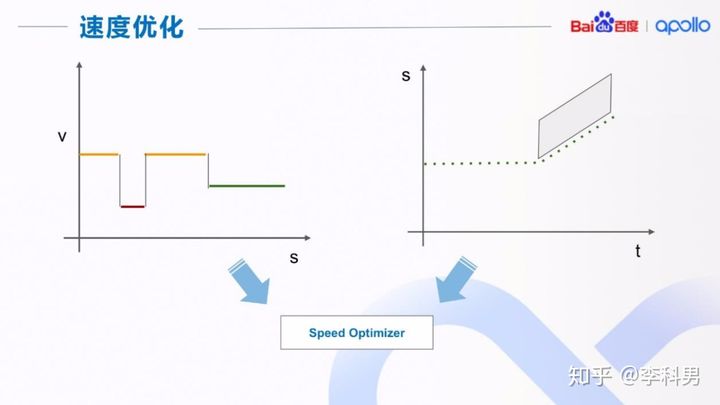
        我们在很多情况下，出于行车安全或者遵守交规的原因，需要对车辆的速度进行限制。 比如，当路径旁边有行人时，我们要减速慢行;当我们要借道避让时，也要减速慢行。 这样的速度限制可能是对整条路径，比如道路限速，也有可能是对路径中的一小段，比如减速带。 如右上图所示，沿路径(s)有三种不同的速度限制：道路限速(黄色)，减速带(红色)，和行人(绿色)。 为了得到整条路径的综合限速，我们把这几种限速集成到一起，如右下图所示。

       得到了路径上的速度边界后，我们就可以利用 ST 图来求解时间上的位置边界。那如何分析ST图呢？上图是一个简单的 ST 图的例子，我们用这个例子来简单解释我们为什么需要 ST 图以及如何从 ST 图上得到时间上的位置边界。 左图是一个简单的驾驶场景，右侧灰色方框代表自动驾驶主车，蓝线是主车的路径；左侧黑色方框代表障碍车，红线是障碍车的预测行驶轨迹。 把障碍车的预测轨迹和主车的路径的交汇关系在 ST 图中表示出来，就如右图所示。 t1 为障碍车预测轨迹和主车路径的交汇时间; s1，s2 为交汇时障碍车在主车路径上的位置; s1 代表车尾位置，s2 代表车头位置。

       在 ST 图中，我们的目标是找到一条不和障碍物碰撞的曲线。同时，曲线还需要满足我们之 前计算的路径上的速度限制，即曲线的斜率不能超过 v 的限制边界(右上图)。 找到最优的一条曲线后，我们根据曲线计算时间上的位置限制边界。 例如，如果我们找到红色的曲线为最优曲线，时间上的位置限制就为红虚线段。 在 x，y 平面中，就表现为主车在障碍车换道前进行超车。反之，绿色的曲线和绿色虚线段 表示主车在障碍车换道后，进行跟随。 

（3）纵向规划的挑战

       纵向规划会面临什么挑战呢？

       I、首先存在博弈的挑战。以上图为例，自动驾驶车前方的左转绿灯亮起并准备左转，这时，一辆电动车突然出现在左前方，准备快速横穿马路。这种情况，人类驾驶员会怎么开呢？人类司机会和电动车司机迅速对一下眼神，通过眼神比较气势谁猛，另一方就会主动地让对方。当然这有开玩笑的成分。但在决策上这个场景并不好处理，它是一个博弈的过程，自动驾驶车不能一开始就决定无视还是让步，所以在很多时候要在激进和保守之间掌握一个平衡点，这需要不同的参数和不同的模式去处理不同场景。

       II、除此之外，感知和预测带来的困难也会使纵向规划面临挑战。

       可以看下图中右上方连续两张相似的图，在第二张图里你会发现有人突然从车前冲出来，俗称叫做“鬼探头”，也就是盲区。对于这种情况，感知需要提前检测到盲区，车辆进行减速，规避可能的安全隐患。

       预测给规划带来的挑战出现在左下角（上图）的场景里。此时，自动驾驶车的右前方行驶着一辆面包车，面包车前边有一辆速度很慢的自行车，一般人类司机会主动预测面包车极有可能向左变道。但这类场景对预测模块提出了很大的挑战，如果缺乏这类预测，自动驾驶车辆的后续应对同样挑战不小。

       III、自动驾驶还有一些极端的情况，需要考虑到横纵向协调配合。上图是一个非常极限的车辆加塞案例：自动驾驶车正在高速行驶时，右侧的一辆慢车突然加塞，一般人类司机会选择打方向避让，如果当时左车道没有车，甚至会向左变道，如果左车道有车，他也会扭一点方向进行避让。这类处理就需要横纵向规划的配合，共同解决极端情况。比如从纵向规划来说，当时已经无法保持安全车距，规划需要做到的是保证不相撞，并尽快拉开车距，而不是一脚刹到底。

 四、Apollo 规划算法解析

Apollo的Planning分为参考线平滑、决策、路径规划、速度规划等部分。

4.1 Apollo 整体架构

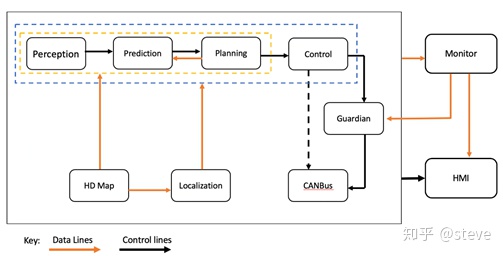
       Apollo系统中的planning模块，整合了决策和规划两个功能。它的功能是依据导航给出的宏观全局路径，并结合当前路段的实际情况进行合理决策，从而规划出一条安全且舒适的轨迹。

4.2 上下游接口分析

a) 输入：

i. HdMap：高精度地图信息

ii. Routing：全局导航信息

iii. Prediction：预测障碍物信息（大小，轨迹等）

iv. TrafficLight

v. Localization：车辆定位信息

vi. Chassis：车辆底盘信息

b) 输出

ADCTrajectory：自车的局部轨迹信息

其中具体的接口数据类型定义，可以参考对应的proto文件，这里也就不展开描述了。

4.3 整体框架

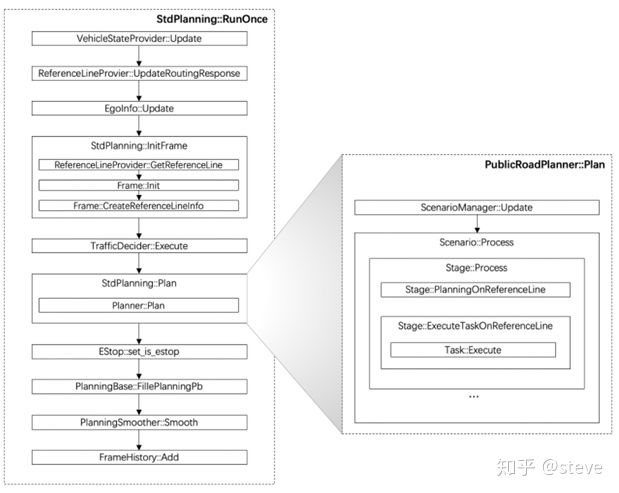
4.4 EM planner 【存在于Apollo 3.0 ----Apollo3.5】

EM-Planner是具体的规划实施类，它基于高精地图、导航路径及障碍物信息作出实际的驾驶决策，包括路径、速度等方面。

• 首先使用DP（动态规划）方法确定初始的路径和速度，再利用QP（二次规划）方法进一步优化路径和速度，以得到一条更平滑的轨迹，既满足舒适性，又方便车辆操纵。
• 基于样条的车辆轨迹优化二次规划，为了寻求更优质更平滑，体感更好的路径，需要使用二次规划的方法寻找。需要的限制条件有：曲率和曲率连续性、贴近中心线、避免碰撞。

（1）EM算法解析

具体EM 算法解析见以下博客：

1. 《自动驾驶之轨迹规划6——Apollo EM Motion Planner》
2. 《Apollo 6.0 规划算法解析》
3. 百度专利《用于自动驾驶车辆的基于DP和QP的决策和规划 [发明]https://cprs.patentstar.com.cn/Search/Detail?ANE=9DGC9CHA6BEA9CDE8AHA7DEA9EEG9BFB7ACA9ABA9BFA9HBF》PDF

（2）二次规划（QP）样条路径

在以上知识基础上，这里补充一下二次规划（QP）样条路径是如何实现的。

（参考《技术文档 | 二次规划（QP）样条路径》）

具体步骤如下：

（a）获得路径长度

      路径定义在 station-lateral坐标系中。参数 s 的取值范围为车辆的当前位置到默认规划路径的长度。

（b）获得样条段

      将路径划分为段，每段路径用一个多项式来表示。

（c）定义样条段函数

       每个样条段  都有沿着参考线的累加距离。每段的路径默认用5阶多项式表示：

（d）定义每个样条段优化目标函数

 

（e）将开销（cost）函数转换为QP公式

       QP 公式如下所示：

       下面是将开销（cost）函数转换为QP公式的例子：

       且： 

 

        且：

        然后得到，

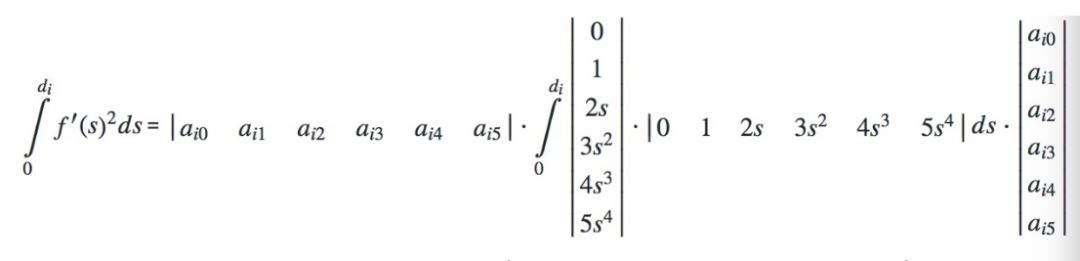
       从聚合函数中提取出常量得到，

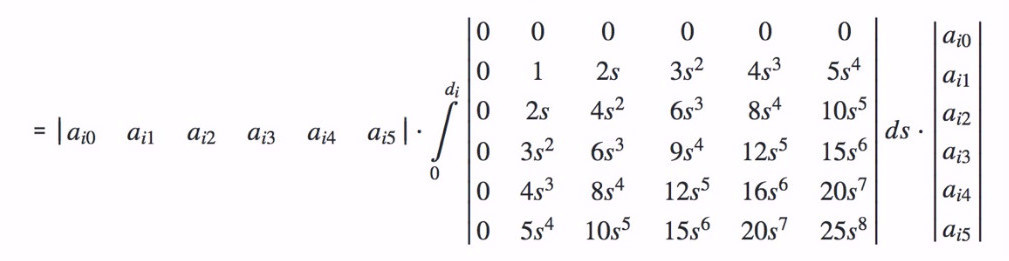
        最后得到，

        请注意我们最后得到一个6阶的矩阵来表示5阶样条插值的衍生开销。

        应用同样的推理方法可以得到2阶，3阶样条插值的衍生开销。

 （a）初始点约束

       假设第一个点为，和，其中表示横向的偏移，并且规划路径的起始点的第一，第二个点的衍生开销可以从计算得到。将上述约束转换为QP约束等式，使用等式：

       下面是转换的具体步骤：

且：

 且：

      其中，是包含的样条段的索引值。

  （b）终点约束

       和起始点相同，终点也应当按照起始点的计算方法生成约束条件。

       将起始点和终点组合在一起，得出约束等式为：

   （c）平滑点约束

        该约束的目的是使样条的节点更加平滑。假设两个段  和  互相连接，且的累计值为。计算约束的等式为：

       下面是计算的具体步骤：

 然后，

 将代入等式。

同样地，可以为下述等式计算约束等式：

   （c）点采样边界约束

       在路径上均匀的取样个点，检查这些点上的障碍物边界。将这些约束转换为 QP 约束不等式，使用不等式：

       首先基于道路宽度和周围的障碍物找到点的下边界，且。计算约束的不等式为：

同样地，对上边界，计算约束的不等式为：

 4.5 Public Road轨迹规划算法（亦称作分段加加速度优化算法，即piecewise jerk optimization）【存在于Apollo 5.0 ----Apollo6.0】

  与之前EM规划和Lattice规划不同，Apollo 5.0版本使用的路径规划，更加的灵活方便，原因主要是采用了数值优化的思想，通过边界约束等，保证了密集障碍物场景的灵活性。 而之前的lattice等算法由于采样的局限，导致在复杂环境下可能存在无解的情况。

▃ ▄ ▅ ▆ ▇ █为什么要抛弃EM  planner采用piecewise jerk optimization？

            （该问题及其解答见Apollo GitHub中的Issues——path optimization and piecewise jerk optimization #9599 中）

答案：我们的规划任务实际上分为路径规划和速度规划。您提到的更改是在路径规划方面，以使用piecewise_jerk_path_optimizer（即QP）处理静态障碍。在速度规划上，我们仍然使用 DP + QP(piecewise_jerk_speed_optimizer) 框架。
        在piecewise_jerk_path_optimizer中，不考虑与上一帧路径的距离，我们只考虑当前状态，或者说路径应该始终与当前状态一致，这足以让路径至少与当前状态平滑连接，我们不真的不需要与未来的道路保持一致。

       DP非常耗时。其次，有时我们可能会因为分辨率和采样点的位置而无法找到路径。我们目前的解决方案是：

• 根据地图、交通规则和障碍物找到路径边界。里面的区域是“可驾驶的”。
• 然后使用分段jerk算法来寻找路径。它解决了DP解决方案中的上述两个主要问题。

参考：

（1）《分享回顾 | Apollo 轨迹规划技术分享》 微信公众号文章 Apollo开发者社区 

（2）百度2020年论文《Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform》百度高级架构师 Zhang Yajia

（3）CSDN 系列博客

        《Apollo 算法阅读之Public Road轨迹规划算法--路径规划(含源代码）》

        《Apollo 算法阅读之Public Road轨迹规划算法--速度规划》

         《Apollo 算法阅读之Public Road轨迹规划算法--整体流程》

（1）轨迹规划综述

        轨迹规划主要指考虑实际临时或者移动障碍物，考虑速度，动力学约束的情况下，尽量按照规划路径进行轨迹规划。

       轨迹规划的核心就是要解决车辆该怎么走的问题。轨迹规划的输入包括拓扑地图，障碍物及障碍物的预测轨迹，交通信号灯的状态，还有定位导航、车辆状态等其他信息。而轨迹规划的输出就是一个轨迹，轨迹是一个时间到位置的函数，就是在特定的时刻车辆在特定的位置上。

       轨迹规划的目标是计算出安全、舒适的轨迹供无人驾驶车辆完成预定的行驶任务。安全意味着车辆在行驶过程中与障碍物保持适当的距离，避免碰撞；舒适意味着给乘客提供舒适的乘坐体验，比如避免过急的加减速度，在弯道时适当减速避免过大的向心加速度等等；最后，完成行驶任务指规划出的轨迹要完成给定的行驶任务，不能因为过于保守的驾驶导致不可接受的行驶时间。

（2）无人驾驶的位形和状态

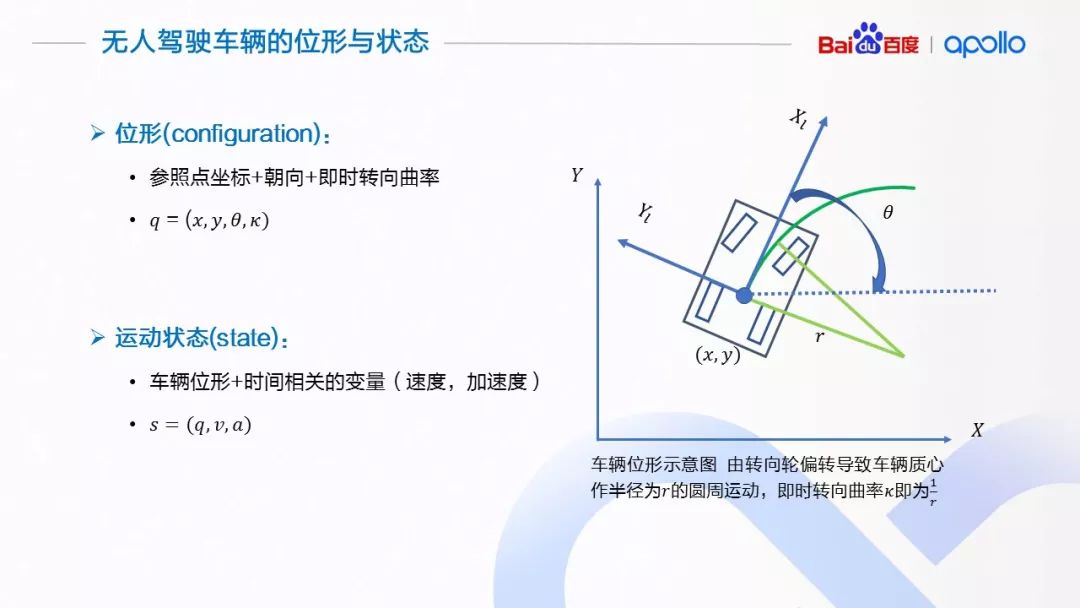
        这里对轨迹规划问题作正式的定义。首先，我们介绍两个机器人领域的概念：位形是在所研究的规划问题中，能够唯一性的表达机器人状态的最小一组变量。变量的数量称为位形的维度。这里需要注意的是，位形空间的维度，即使对于同一个机器人来讲，所研究的问题不同，维度也是不同的。比如，对一个人形机器人来讲，如果规划问题是在三维空间中移动，位形需要由参照点的变换矩阵，关节的伸展角度组成；如果规划问题是作物体的操作，则在前面问题位形空间的基础上，还要增加机器人手指关节的伸展角度等。

        对于无人驾驶车辆来讲，最简单的位形描述需要使用3个变量：车辆某个参照点的坐标(x, y)，以及车辆的朝向θ来表达车辆的构型，这也是很多参考文献中，对于非和谐车辆系统的位形表达方式。对于我们专门为有人乘用的无人驾驶车辆作轨迹规划的问题来讲，更好的位形组成在上面的3个变量基础上加入车辆的即时转向曲率 κ：如果车辆的导向轮保持一定的角度，车辆会做圆周运动。这个圆周运动的半径就是即时转向曲率 κ 。加入 κ，有助于控制模块获得更准确的控制反馈，设计更为精细平稳的控制器。

（3）轨迹规划的定义

         轨迹规划的正式定义，计算一个以时间 t 为参数的函数 S ，对于定义域内（[0, t_max]）的每一个 t ，都有满足条件的状态 s ：满足目标车辆的运动学约束，碰撞约束，以及车辆的物理极限。

（4）轨迹规划的难点

       轨迹规划是一个复杂的问题，首先，规划上加入了速度与时间的信息，增加了规划的维度。其次，由于车辆是非和谐系统，具有特殊的运动学约束条件。举个例子，车辆不能独立的横向移动，需要纵向移动的同时才能获得横向偏移。躲避障碍物，特别是高速动态障碍物，也是一个比较困难的问题。对于搭载乘客的无人驾驶车辆来说，非常重要的一个要求是舒适性，规划出的轨迹必须做到平滑，将影响乘客舒适度的因素，比如加速度、向心加速度等等，保持在能够容忍的范围。

       另外，对于无人驾驶车辆来讲，为了处理多变的行车环境，轨迹规划算法需要以短周期高频率运行，对算法的计算效率也提出了要求。

（5）Apollo中轨迹规划策略

        在 Apollo 平台中，为了解决规划问题，尤其是从降低计算的复杂性上，采取了对轨迹的路径与速度规划分离的方式。即先确定路径，也就是轨迹的几何形状，然后在已知路径的基础上，计算速度分配。使用这种策略，我们将一个高维度的轨迹规划问题，转换成了两个顺序计算的低维度规划问题：路径规划，借助中间变量路径的累计长度 s，先求解 s 映射到几何形状(x, y, θ, κ)的路径函数；速度规划，再求解时间 t，映射到中间变量 s 与 v，a 的速度函数。

（6）路径规划的目标

      前面提到 Apollo 轨迹规划的策略，我们先看路径规划在这种策略下需要解决的问题：

1. 路径需要有足够的灵活度，用来对复杂城市环境中的障碍物进行避让。

2. 路径的几何特性需要平顺变化，这样车辆在沿路径行驶时才能够保证舒适性。

3. 路径的规划需要遵守车辆的运动学限制条件，比如，路径的曲率、曲率变化率需要限制在符合目标车辆属性的范围之内。

4. 由于 Apollo 平台中采用了路径/速度分离的策略，在路径规划时也需要考虑到当前车辆的运动状态而适当的调整车辆的几何形状。比如在做较大的横向运动的时候，低速和高速下，需要不同的几何形状来保证横向运动的舒适性。

（7）路径规划方法

       在路径规划中，我们借助于弗莱纳坐标系，将当前车辆的运动状态(x, y, θ, κ, v, a)做分解。使用弗莱纳坐标系的前提是具有一条光滑的指引线。一般情况下，将指引线理解为道路中心线，车辆在没有障碍物情况下的理想运动路径。我们这里的光滑的指引线是指指引线的几何属性可以到曲率级别的光滑。指引线的光滑性至关重要，因为其直接决定了在弗莱纳坐标系下求得轨迹的平顺性。

       在给定一条光滑指引线上，我们按照车辆位置，将其投影到指引线上，以投射点为基础，将地图坐标系下当前车辆的运动状态(x, y, θ, κ, v, a)进行分解，获得沿着指引线方向的位置、速度、加速度，以及相对于指引线运动的位置、 “速度”、 “加速度”。这里打引号的原因是横向的“速度”、“加速度”并非通常意义上位移对时间的一阶/二阶导数，而是横向位移对纵向位移的一阶/二阶导数，它们描述了几何形状的变化趋势。

（8）在弗莱纳坐标系下做轨迹规划的优点

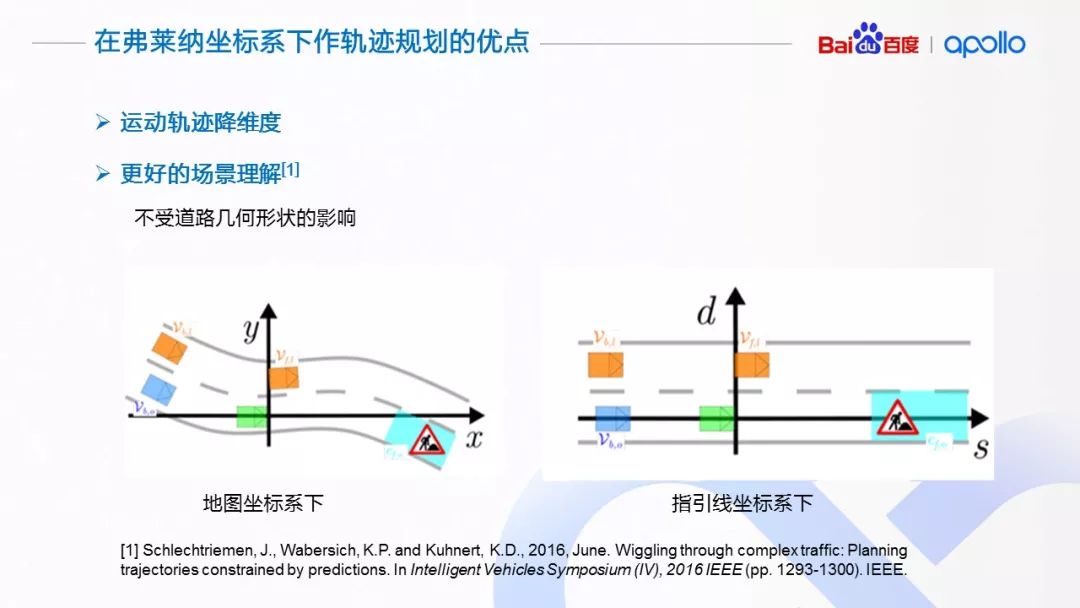
       在弗莱纳坐标系下做运动规划的好处在于借助于指引线做运动分解，将高维度的规划问题，转换成了多个低维度的规划问题，极大的降低了规划的难度。另外一个好处在于方便理解场景，无论道路在地图坐标系下的形状与否，我们都能够很好的理解道路上物体的运动关系。相较直接使用地图坐标系下的坐标做分析，使用弗莱纳坐标，能够直观的体现道路上不同物体的运动关系。

（9）路径规划——分段加加速度优化算法

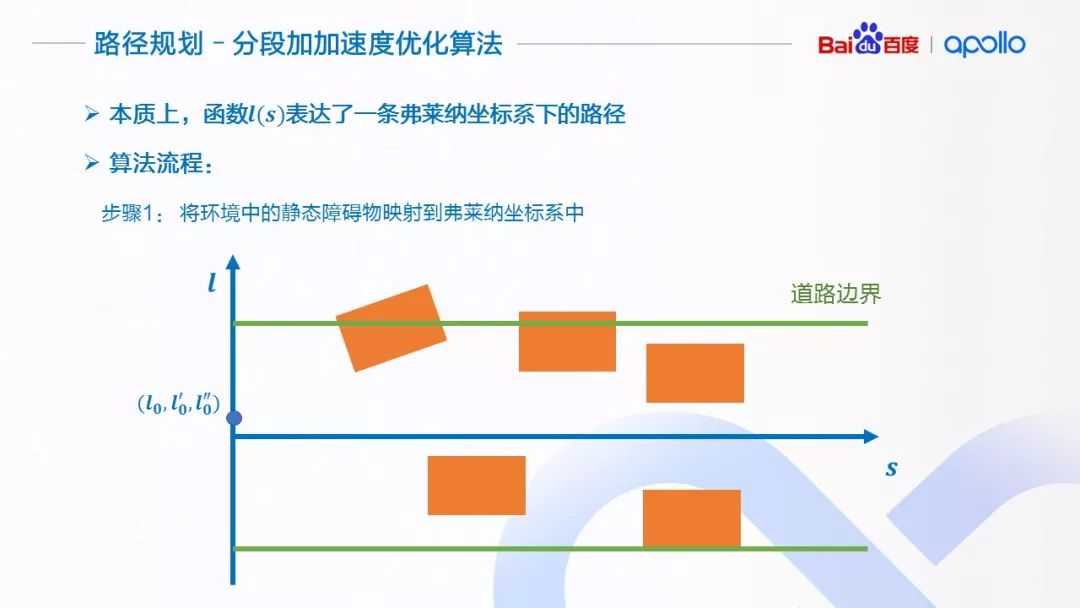
       在弗莱纳坐标系下的函数l(s)，表达了以指引线为参考，相对于指引线的几何形状；通过转换到地图坐标系下，就表达了在地图坐标系的路径。所以，本质上，路径规划问题在弗莱纳坐标系下，就是一个计算函数l(s)的过程。

       为了解决这个问题，这里介绍由我提出的分段加加速度优化算法（Piecewise Jerk Path Optimization Algorithm），我们先来看一下算法的流程：

       第一步，我们将环境中的静态障碍物从地图坐标系映射到依据指引线的弗莱纳坐标系下（红色方框）。

        第二步，沿指引线的 s 轴方向，使用 Δs 将 s 方向等距离离散化。根据障碍物的信息、道路的边界，计算出每一个离散点所对应的可行区域(l_min^i，l_max^i )。为了方便描述，我们将无人驾驶车简化成一个点。为了避免碰撞，在计算可行区域的时候可以留出适当的缓冲区间。

       第三步，介绍优化算法使用的优化变量。对于每一个离散点i，我们将该点的横向偏移 l_i，横向偏移相对于s的一阶和二阶导数 l_i^′ 和 l_i^″作为优化变量。l_i^′ 和 l_i^″可以近似理解为横向运动的“速度”与“加速度”。他们的大小决定了车辆靠近与偏离指引线的趋势。

       假设每两个离散点之间，有一个常三阶导数项l_(i→i+1)^‴连接着相邻的离散点， 这个“常”三阶导数项可以由相邻的二阶导数通过差分的方式计算得到。在优化的迭代过程中，l(i→i+1)^‴ 会随着相邻点li^″  与l_(i+1)^″  的变化而变化，但l_(i→i+1)^‴在两个离散点之间会保持不变。

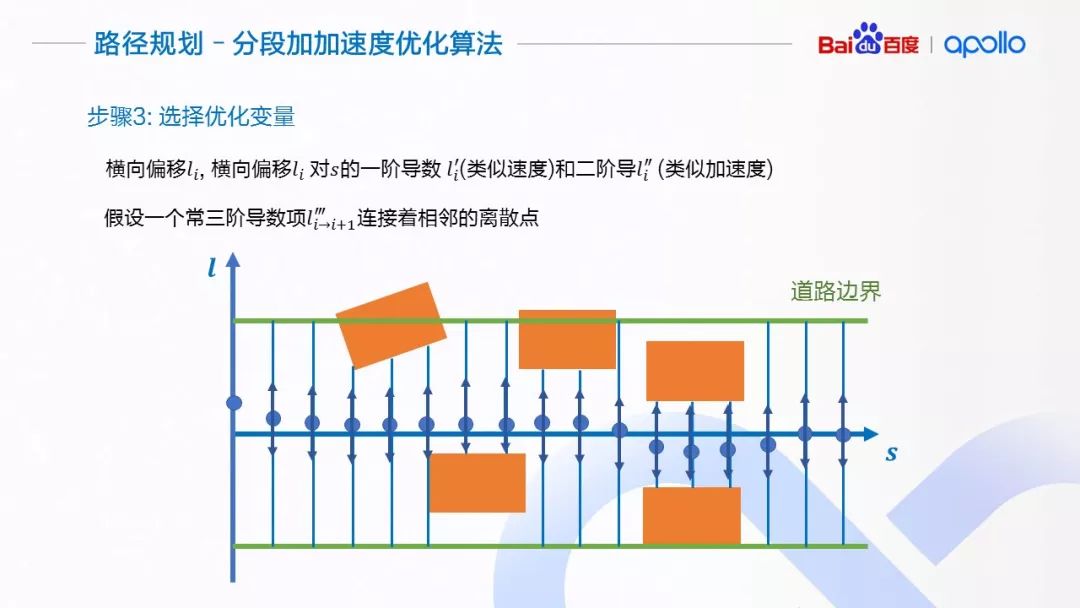
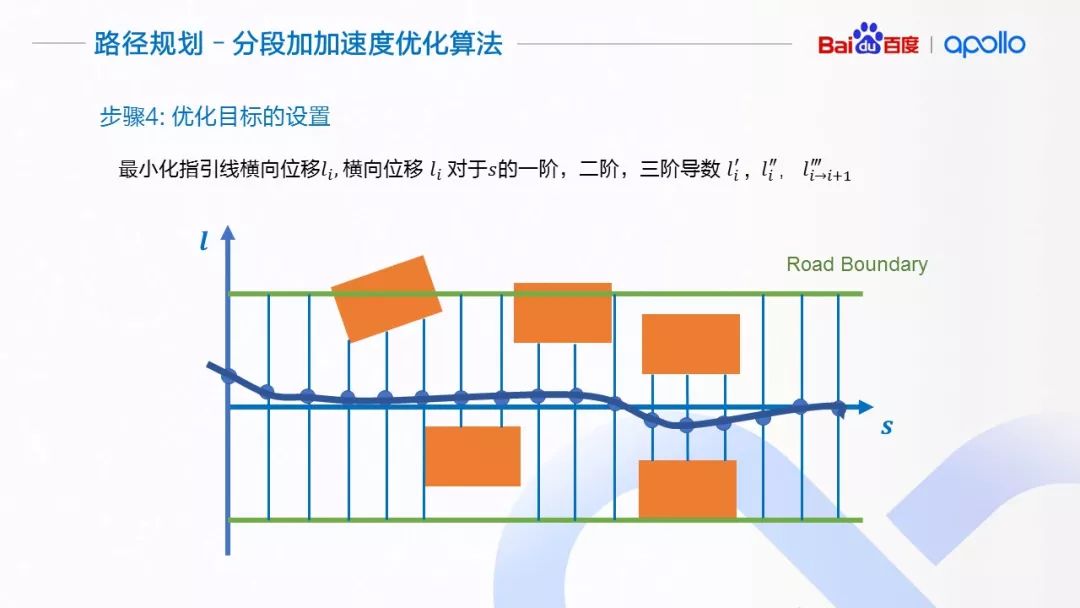
       第四步，设置优化目标。首先，对于路径来讲，在没有环境因素影响的情况下，我们希望它尽可能的贴近指引线。对于一阶、二阶与三阶导数，我们希望它们尽可能的小, 这样可以控制横向运动的向心加速度，保证路径的舒适性。

（10）横向路径规划算法完整描述

1.  在lane change decider中会进行referline_info的数量查看，如果没有开启换道功能，那么始终只有当前一个referline_info，删去换道路径；否则保留多个referline_info.
2.  在lane_borrow_decider判断是否当前在借道场景，
        如果在借道场景，判断是否self_counter是否大于6，如果是退出borrow模式，否则保持借道； 
        如果不在借道场景，判断是否需要换道，判断是否需要换道，主要包括：
        a.速度小于20km/h
        b.远离交叉口；
        c.障碍物是长期静止的;（即障碍物长期影响原有参考线）
        d.远离终点的;
        e.障碍物在有限范围内（35m）
        当同时满足上述条件时，判断左右是否具备超车车道（查询地图），如果存在可以做超车的，加入到换道列表中，从而进入超车模式.      
3.  根据换道列表及当前场景状态，生成不同类型的boundary，包括fall back与self，如果是超车状态生成 left borrow, right borrow.
4.  初始化道路边界，初始化障碍物边界，如果前方已生成的Boundary的道路中心仍然被堵死，就截取到障碍物点；    
5.  通过不同的Boundary，生成不同的路线；具体可参考另一篇文章：Apollo-public road planner-路径规划
6.  path_assessment_decider进行路线安全评估验证，随后如果没有障碍物遮挡，那么safe_counter++。对生成的轨迹进行排序，选择最优的；,如果self轨迹是首选轨迹，self_counter++，当大于6时，会退出超车模式，最后会退出超车模式；
7.  path_decider就是如果前方仍然存在遮挡物的话，把路线截断到那儿，并加入longitudinal decision，从而使得速度规划方面可以在此处停止；

       下面，我们回顾一下这个算法，算法的输入由四个部分组成：

1. 光滑的道路指引线，用于在弗莱纳坐标系下的运动分解。

2. 当前无人驾驶车辆的运动状态，包括位置、朝向、即时转向、速度与加速度。车辆运动状态会依照光滑指引线进行分解。

3. 环境中静态障碍物的信息，投影到指引线上。

4. 车辆自身的属性，运动学模型等，用于计算优化过程中合理的变量限制条件。

       算法的变量每一个离散点的横向位移，横向位移对指引线纵向长度 s 的一阶、二阶导数，对于有 n 个输入点的问题，优化变量有 3∗n 个。对于限制条件，首先横向位移li需要在相对应的安全区间之内(l_min^i,l_max^i )。对于 l_i^′, 〖l_i〗^″, l(i→i+1)^‴的取值范围，需要根据当前车辆移动速度, 车辆的动力学模型计算，涉及到具体的车辆模型。

       一个非常关键的约束条件是路径的连续性。我们假设相邻两点之间有一个常三阶导数量 l_(i→i+1)^‴来连接，我们需要确定经过这个常三阶导数量l(i→i+1)^‴，相邻两个点的l, l^′, l″的数值能够吻合。举个例子，两个点之间就好比可以拉伸的绳子，l(i→i+1)^‴决定了可以拉伸的程度，这两个式约束决定了在绳子拉伸的过程中保证绳子不被拉断。

优化目标函数

       算法的优化目标，是减小横向位移的零阶，一阶，二阶和三阶导数，使路径尽可能贴近指引线的同时保证舒适性。当然，我们也可以根据需求，选择性的加入与边界距离的优化目标，使车辆与障碍物保持适当距离。分段加加速度算法由于其大密度分段的特性，使得能够表达的路径具有很高的灵活性，能够解决城市道路中（特别是国内拥挤的环境J）的路径规划问题；并且，由于是以加加速度级别的控制变量来改变路径的形状，能够做到曲率级别的连续性，保证了路径的平滑舒适。

（11）速度规划算法——启发式速度规划+分段加加速度算法

1.  Speed_bounds_prior_decider:
       首先，将障碍物的轨迹映射到s-t graph，随后计算出障碍物在最优路径上的st轨迹交集（prior过程，障碍物在速度方面不存在decision，因此此次计算轨迹是withoutdecision），并将其放置boundaries集合中，随后设置速度最大限制（沿规划好路径），最后，st_graph_data保存boundaries,speed_limit等.
2.  DP_ST_SPEED_OPTIMIZER：
       根据上述的boundaries，进行计算启发式速度曲线搜索，得到最优轨迹；
3.  SPEED_DECIDER：
       根据上述的speed曲线，来初步判断对障碍物的decision，其中行人需要特别处理，设置相应的决策行为；
4.  SPEED_BOUNDS_FINAL_DECIDER：
       重新计算障碍物stboundary，然后根据障碍物的decision，确定速度的边界；
5.  PIECEWISE_JERK_SPEED_OPTIMIZER
       基于osqp进行速度曲线的数值优化计算，得出最优曲线
 

速度规划的目标

下一步，我们来看怎样为计算出的路径分配速度。对于速度规划，有如下要求：

1. 速度分配具有灵活性，能够避让复杂、拥挤的城市环境中的众多移动障碍物。

2. 速度分配需要遵守车辆运动学的限制条件， 比如最大速度、加速度、加加速度等，确保规划出的轨迹车辆实际可以执行。

3. 规划的速度分配需要遵守考虑交通法规的限制，在限速范围内规划。

4. 规划的速度分配需要完成到达指定位置或者指定速度的任务，并且在保证舒适度的前提下，完成时间尽可能的短。

   

   速度规划的策略

       在 Apollo 平台的实现中，采用了结合启发式速度规划和分段加加速度算法相结合的方式来解决速度规划问题。启发式速度规划提供考虑了动静态障碍物、路径几何信息、道路信息、舒适度、目标速度和地点多种因素综合下的速度规划粗略估计；分段加加速度算法对启发是速度规划提供的粗略分析进行平滑，输出安全舒适的速度分配。

       在启发式速度规划中，采用了一个非常好的分析工具，路径-时间障碍物图（Path-Time Obstacle Graph）。路径-时间障碍物图非常适合在确定了路径的情况下，考虑动静态障碍物的规避问题。这个分析工具的核心思想就是将考虑了本车和周围障碍物几何形状和预测轨迹的情况下，将障碍物的轨迹投影到已经确定的本车路径上。障碍物所代表的含义是在何时（t）与何地（s）本车会与障碍物发生碰撞。

（a）启发式速度规划

启发式速度规划

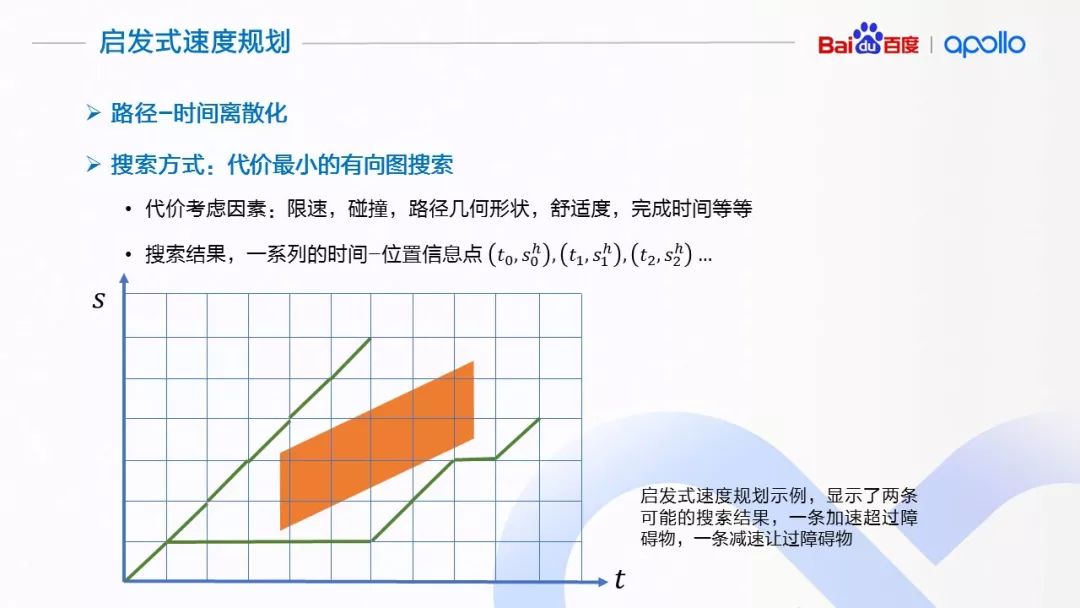
       在 Apollo 的实现中，路径-时间障碍物图根据时间轴 t 和沿路径的累计距离s离散化，形成等距离、等时间的网格状图。然后根据需求，将各种因素使用不同的权重，建模成一个单一熟知的代价函数，每一个网格的节点会赋予一个代价，相邻网格之间的边也视为代价的一部分，用来建模加速度。整个过程可以看成是一个图搜索的过程，搜索出一个代价最优的路径。搜索的结果就是一系列的路径距离与时间的序列，代表何时（t），我们期望无人驾驶车到达何地（s）。

（b）速度平滑上的分段加加速度算法

分段加加速度平滑算法

        启发式速度规划的粗略结果只能提供位置，缺乏控制所需要的更高维信息，不适合控制模块直接使用。产生的结果需要进一步的平滑才能满足舒适度要求。我们进一步做平滑处理的方法使用的是分段常加加速度算法，其主要思想类似于前面介绍的路径优化算法，在给定趋近启发式速度规划结果的情况下，调整启发式速度规划，提高速度分配的平滑性。

分段加加速度算法

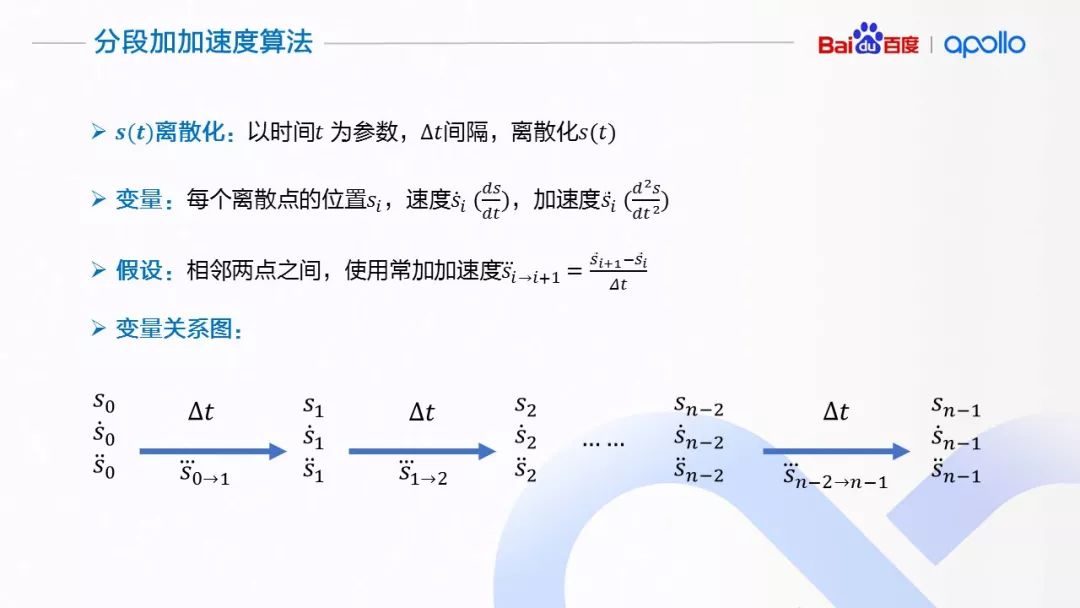
       下面具体介绍应用在速度平滑上的分段加加速度算法。由于与前面的路径上使用的算法类似，相似的地方就不再赘述。该算法以时间作为离散参数（可以使用启发式算法使用的时间间隔），以每个离散点的位置、速度、加速度作为优化变量，并且假设相邻两点之间，是一个由相邻加速度变量差分得到的加加速度。

优化目标函数设置

       在优化函数的设置上，与前面算法相似的地方是惩罚加速度与加加速度的以获得舒适的乘坐体验。不同的一个优化目标是希望位置变量与启发式规划所得到的位置信息尽可能贴近。启发式规划所得到的位置信息蕴含了根据路径几何形状、道路限速等等所做出的计算，这些计算绑定在相应的位置上，所以优化之后的轨迹需要贴近于相应的启发式结果才能体现启发式规划所做的选择。

（12）算法评价与改进

算法评价与改进

       大家可能有的一个问题是，在速度规划的时候，为什么分成启发式的速度规划与分段加加速度算法结合的形式？为何不直接使用加加速度算法进行求解？主要的问题在于在速度规划的时候，进行离散的维度、时间，也是优化目标的一部分。

       位置与时间同为优化变量，与位置相关的限制条件， 比如路径曲率、道路限速信息等等，会影响到达位置的时间；而时间的变化又会引起优化速度的变化，进而导致位置发生变化。这就导致了一种变量间耦合变化的情况。启发式速度规划使用粗略的方法，近似解决了位置 s 决定的限制条件与时间 t 相互耦合的问题，使时间成为了常量。

       但是，这样做也有很明显的不利影响，启发式速度规划的粒度影响了搜索的质量，在搜索过程不够准确，不能反映车辆的动态变化。平滑时单纯贴近启发式速度规划，速度规划并非最优。

(13) Public Road横向路径规划源码学习

《Apollo 算法阅读之Public Road轨迹规划算法--路径规划(含源代码）》

       主要介绍apollo 5.0版本内使用的轨迹规划算法----public road，该算法的核心思想是PV解耦，即Path-Velocity的解耦，其主要包含两个过程：1.路径规划，2.速度规划。

       路径规划其实已经发展很多年，从早期的机器人到现在的无人驾驶，主要的方法包括 采样法，图搜索法，数值优化法等，具体可以查阅相关文献阅读。本篇文章主要讲述apollo轨迹规划模块里面的路径规划，有时间再更新之后的速度规划。

       与之前EM规划和Lattice规划不同，当前5.0版本使用的路径规划，更加的灵活方便，原因主要是采用了数值优化的思想，通过边界约束等，保证了密集障碍物场景的灵活性。 而之前的lattice等算法由于采样的局限，导致在复杂环境下可能存在无解的情况。言归正传，apollo在内部的路径规划里主要包括以下几个步骤。 （由于场景的差异性，task与stage也有所不同，因此本文只讲述lane follow scenario）。

Status LaneFollowStage::PlanOnReferenceLine(
    const TrajectoryPoint& planning_start_point, Frame* frame,
    ReferenceLineInfo* reference_line_info) {
  if (!reference_line_info->IsChangeLanePath()) {
    reference_line_info->AddCost(kStraightForwardLineCost);
  }

       我们通过 lane_follow_stage.cc文件中 Status LaneFollowStage::PlanOnReferenceLine 函数可以看到具体工作细节。

       首先，会根据

 for (auto* optimizer : task_list_) {
    const double start_timestamp = Clock::NowInSeconds();
    ret = optimizer->Execute(frame, reference_line_info);
    if (!ret.ok()) {
      AERROR << "Failed to run tasks[" << optimizer->Name()
             << "], Error message: " << ret.error_message();
      break;
    }
  }

       当前先验信息判断是否当前参考线是可换道的车道，如果不是那么增加cost。 随后，开始了task的process过程，不同的stage有不同的task，具体可通过 conf/scenario文件夹下的pb.txt，例如：

scenario_type: LANE_FOLLOW
stage_type: LANE_FOLLOW_DEFAULT_STAGE
stage_config: {
  stage_type: LANE_FOLLOW_DEFAULT_STAGE
  enabled: true
  task_type: LANE_CHANGE_DECIDER
  task_type: PATH_LANE_BORROW_DECIDER
  task_type: PATH_BOUNDS_DECIDER
  task_type: PIECEWISE_JERK_PATH_OPTIMIZER
  task_type: PATH_ASSESSMENT_DECIDER
  task_type: PATH_DECIDER
  task_type: RULE_BASED_STOP_DECIDER
  task_type: SPEED_BOUNDS_PRIORI_DECIDER
  task_type: DP_ST_SPEED_OPTIMIZER
  task_type: SPEED_DECIDER
  task_type: SPEED_BOUNDS_FINAL_DECIDER
  task_type: PIECEWISE_JERK_SPEED_OPTIMIZER
  task_type: DECIDER_RSS

       上述task中，根据名称可以看出，path都是与路径相关，从rule_based之后则是与速度规划相关。

       按照任务顺序：

1. lane change decider： 该任务主要是用来处理refer_line_info，内部有个状态机，根据换道成功时间与换道失败时间以及当前位置与目标位置来切换状态，以此来处理refer_line_info的changelane信息。
2. lane borrow：该任务相对复杂，主要涉及了一些rules，判断是否可以进行借道超车，rules包括：距离信号交叉口的距离，与静态障碍物的距离，是否是单行道，是否所在车道左右车道线是虚线等规则，以此来判断是否可以借道超车；
3. path bound decider：根据上一任务的结果，来生成相应的道路边界信息，包括三部分:原车道（左右横向位移0.5m），左超车道，右超车道（具体横向位移根据HDMap及周围障碍物在sl坐标系下的位置所决定）；path bound的结果将会作为下一步结果的边界约束，具体原理可查看apollo公开课。

       根据上述边界可以构建optimization method。

       由此开始了第四个任务：piecewise jerk path optimazation。原理可请查看该篇博文《公开课路径规划原理》。

       本篇文章主要讲述内部的代码推理，主要涉及osqp优化求解问题。

    bool res_opt =
        OptimizePath(init_frenet_state.second, end_state,
                     path_boundary.delta_s(), path_boundary.boundary(),
                     ddl_bounds, w, &opt_l, &opt_dl, &opt_ddl, max_iter);

       上述是优化问题的函数接口，

    
bool PiecewiseJerkPathOptimizer::OptimizePath(
std::vector<double>* dx, std::vector<double>* ddx, const int max_iter) {
//初始化状态，将问题转化为 qp问题
  PiecewiseJerkPathProblem piecewise_jerk_problem(lat_boundaries.size(),
                                                  delta_s, init_state);
 
  piecewise_jerk_problem.set_end_state_ref({1000.0, 0.0, 0.0}, end_state);
  if (end_state[0] != 0) {
    std::vector<double> x_ref(lat_boundaries.size(), end_state[0]);
    piecewise_jerk_problem.set_x_ref(10.0, x_ref);
  }
// 初始化设置各项权重
  piecewise_jerk_problem.set_weight_x(w[0]);
  piecewise_jerk_problem.set_weight_dx(w[1]);
  piecewise_jerk_problem.set_weight_ddx(w[2]);
  piecewise_jerk_problem.set_weight_dddx(w[3]);
 
  piecewise_jerk_problem.set_scale_factor({1.0, 10.0, 100.0});
 
  auto start_time = std::chrono::system_clock::now();
//初始化各项变量的边界
  piecewise_jerk_problem.set_x_bounds(lat_boundaries);
  piecewise_jerk_problem.set_dx_bounds(-FLAGS_lateral_derivative_bound_default,
                                       FLAGS_lateral_derivative_bound_default);
  piecewise_jerk_problem.set_ddx_bounds(ddl_bounds);
  piecewise_jerk_problem.set_dddx_bound(FLAGS_lateral_jerk_bound);

  bool success = piecewise_jerk_problem.Optimize(max_iter);

       上面是qp问题求解的入口，调用osqp标准求解库，

  //首先进行osqp配置
  OSQPSettings* settings = SolverDefaultSettings();
  settings->max_iter = max_iter;
 
  OSQPWorkspace* osqp_work = osqp_setup(data, settings);
 
  osqp_solve(osqp_work);
 
 
 
PiecewiseJerkProblem::FormulateProblem()//该函数是重点，主要包含了目标函数与响应约束的建立，以及目标函数的offset补偿。

// x(i)^2 * (w_x + w_x_ref)
  for (int i = 0; i < n - 1; ++i) {
    columns[i].emplace_back(
        i, (weight_x_ + weight_x_ref_) / (scale_factor_[0] * scale_factor_[0]));
    ++value_index;
  } 
  // x(n-1)^2 * (w_x + w_x_ref + w_end_x)
  columns[n - 1].emplace_back(
      n - 1, (weight_x_ + weight_x_ref_ + weight_end_state_[0]) /
                 (scale_factor_[0] * scale_factor_[0]));
  ++value_index;
 
  // x(i)'^2 * w_dx
  for (int i = 0; i < n - 1; ++i) {
    columns[n + i].emplace_back(
        n + i, weight_dx_ / (scale_factor_[1] * scale_factor_[1]));
    ++value_index;
  }
  // x(n-1)'^2 * (w_dx + w_end_dx)
  columns[2 * n - 1].emplace_back(2 * n - 1,
                                  (weight_dx_ + weight_end_state_[1]) /
                                      (scale_factor_[1] * scale_factor_[1]));
  ++value_index;
 
  auto delta_s_square = delta_s_ * delta_s_;
  // x(i)''^2 * (w_ddx + 2 * w_dddx / delta_s^2)
  columns[2 * n].emplace_back(2 * n,
                              (weight_ddx_ + weight_dddx_ / delta_s_square) /
                                  (scale_factor_[2] * scale_factor_[2]));
  ++value_index;
  for (int i = 1; i < n - 1; ++i) {
    columns[2 * n + i].emplace_back(
        2 * n + i, (weight_ddx_ + 2.0 * weight_dddx_ / delta_s_square) /
                       (scale_factor_[2] * scale_factor_[2]));
    ++value_index;
  }
  columns[3 * n - 1].emplace_back(
      3 * n - 1,
      (weight_ddx_ + weight_dddx_ / delta_s_square + weight_end_state_[2]) /
          (scale_factor_[2] * scale_factor_[2]));
  ++value_index;
 
  // -2 * w_dddx / delta_s^2 * x(i)'' * x(i + 1)''
  for (int i = 0; i < n - 1; ++i) {
    columns[2 * n + i].emplace_back(2 * n + i + 1,
                                    (-2.0 * weight_dddx_ / delta_s_square) /
                                        (scale_factor_[2] * scale_factor_[2]));
    ++value_index;
  }
 
上述设置了目标函数，主要包括：
l^2+l'^2+l''^2，以及l'''^2，其中l'''通过l''前后两帧之差与delta_s之比替代。

       osqp内部的核函数矩阵形式是csc格式，需要具体了解该形式的同学，可以百度搜索csc矩阵或通过osqp官方demo学习。

       当设计完目标函数矩阵后，开始设置相应的约束,

 
void PiecewiseJerkProblem::CalculateAffineConstraint(
    std::vector<c_float>* A_data, std::vector<c_int>* A_indices,
    std::vector<c_int>* A_indptr, std::vector<c_float>* lower_bounds,
    std::vector<c_float>* upper_bounds) {
  // 3N params bounds on x, x', x''
  // 3(N-1) constraints on x, x', x''
  // 3 constraints on x_init_
 
说的很详细，主要包含 变量边界约束，三个运动学公式约束以及初始状态约束，边界约束主要是横向最大位移、最大速度、最大加速度等，运动学公式主要是 x(i->i+1)''' = (x(i+1)'' - x(i)'') / delta_s等等，可参考我给的博文

       首先是变量约束，通过赋值变量上下边界，完成约束设置。

  // set x, x', x'' bounds
  for (int i = 0; i < num_of_variables; ++i) {
    if (i < n) {
      variables[i].emplace_back(constraint_index, 1.0);
      lower_bounds->at(constraint_index) =
          x_bounds_[i].first * scale_factor_[0];
      upper_bounds->at(constraint_index) =
          x_bounds_[i].second * scale_factor_[0];
    } else if (i < 2 * n) {
      variables[i].emplace_back(constraint_index, 1.0);
 
      lower_bounds->at(constraint_index) =
          dx_bounds_[i - n].first * scale_factor_[1];
      upper_bounds->at(constraint_index) =
          dx_bounds_[i - n].second * scale_factor_[1];
    } else {
      variables[i].emplace_back(constraint_index, 1.0);
      lower_bounds->at(constraint_index) =
          ddx_bounds_[i - 2 * n].first * scale_factor_[2];
      upper_bounds->at(constraint_index) =
          ddx_bounds_[i - 2 * n].second * scale_factor_[2];
    }
    ++constraint_index;
  }

       随后是运动学约束，可能这里各位同学会搞混，按照代码的约束，由于csc就是这样的写法，各位同学可以画一个矩阵，这些约束都是按照constrain index作为序列标号，variables[i]在这里只是调用了第i个变量，后面的-1.0代表该变量的相关系数。以这个for循环为例， 约束形式应该是： 0*variable[0]+0*variable[1]+....-variables[2*n+i]+variables[2*n+i+1] = 0(上下界都是0，因此等于0)正好与之前运动学约束对应。其他的同理。

  // x(i->i+1)''' = (x(i+1)'' - x(i)'') / delta_s 以constrain index作为序列
  for (int i = 0; i + 1 < n; ++i) 
  {
    variables[2 * n + i].emplace_back(constraint_index, -1.0);
    variables[2 * n + i + 1].emplace_back(constraint_index, 1.0);
    lower_bounds->at(constraint_index) =
        dddx_bound_.first * delta_s_ * scale_factor_[2];
    upper_bounds->at(constraint_index) =
        dddx_bound_.second * delta_s_ * scale_factor_[2];
    ++constraint_index;
  }
 
  // x(i+1)' - x(i)' - 0.5 * delta_s * x(i)'' - 0.5 * delta_s * x(i+1)'' = 0
  for (int i = 0; i + 1 < n; ++i) {
    variables[n + i].emplace_back(constraint_index, -1.0 * scale_factor_[2]);
    variables[n + i + 1].emplace_back(constraint_index, 1.0 * scale_factor_[2]);
    variables[2 * n + i].emplace_back(constraint_index,
                                      -0.5 * delta_s_ * scale_factor_[1]);
    variables[2 * n + i + 1].emplace_back(constraint_index,
                                          -0.5 * delta_s_ * scale_factor_[1]);
    lower_bounds->at(constraint_index) = 0.0;
    upper_bounds->at(constraint_index) = 0.0;
    ++constraint_index;
  }
 
  // x(i+1) - x(i) - delta_s * x(i)'
  // - 1/3 * delta_s^2 * x(i)'' - 1/6 * delta_s^2 * x(i+1)''
  auto delta_s_sq_ = delta_s_ * delta_s_;
  for (int i = 0; i + 1 < n; ++i) {
    variables[i].emplace_back(constraint_index,
                              -1.0 * scale_factor_[1] * scale_factor_[2]);
    variables[i + 1].emplace_back(constraint_index,
                                  1.0 * scale_factor_[1] * scale_factor_[2]);
    variables[n + i].emplace_back(
        constraint_index, -delta_s_ * scale_factor_[0] * scale_factor_[2]);
    variables[2 * n + i].emplace_back(
        constraint_index,
        -delta_s_sq_ / 3.0 * scale_factor_[0] * scale_factor_[1]);
    variables[2 * n + i + 1].emplace_back(
        constraint_index,
        -delta_s_sq_ / 6.0 * scale_factor_[0] * scale_factor_[1]);
 
    lower_bounds->at(constraint_index) = 0.0;
    upper_bounds->at(constraint_index) = 0.0;
    ++constraint_index;
  }

       最后是初始状态约束，即最终轨迹的初始状态要与当前车辆状态保持一致。

  // constrain on x_init
  variables[0].emplace_back(constraint_index, 1.0);
  lower_bounds->at(constraint_index) = x_init_[0] * scale_factor_[0];
  upper_bounds->at(constraint_index) = x_init_[0] * scale_factor_[0];
  ++constraint_index;
 
  variables[n].emplace_back(constraint_index, 1.0);
  lower_bounds->at(constraint_index) = x_init_[1] * scale_factor_[1];
  upper_bounds->at(constraint_index) = x_init_[1] * scale_factor_[1];
  ++constraint_index;
 
  variables[2 * n].emplace_back(constraint_index, 1.0);
  lower_bounds->at(constraint_index) = x_init_[2] * scale_factor_[2];
  upper_bounds->at(constraint_index) = x_init_[2] * scale_factor_[2];
  ++constraint_index;

       最后，我们将进行offset 补偿，这里主要指的是 最后的参考线要考虑referline这一因素，即初始解。保证尽可能不要有太大偏差，这样有可能给车辆带来不稳定因素，这里主要是给目标函数进行补偿，目标函数的 ref一项。

       其实目标函数在横向位移上有两项： l^2+(l-ref)^2,因此可以看到为什么在目标函数里，l^2的系数乘以2，在这里将第二项进行了拆解，于是有了offset。 即 -2ref*i，这个就对应了。各位细品。至于为什么不考虑ref^2，因为它是个非负实数，并不包含任何变量，因此不影响梯度下降，从而不影响整个函数的求解。因此在此处省略。

void PiecewiseJerkPathProblem::CalculateOffset(std::vector<c_float>* q) {
  CHECK_NOTNULL(q);
  const int n = static_cast<int>(num_of_knots_);
  const int kNumParam = 3 * n;
  q->resize(kNumParam, 0.0);
 
  if (has_x_ref_) {
    for (int i = 0; i < n; ++i) {
      q->at(i) += -2.0 * weight_x_ref_ * x_ref_[i] / scale_factor_[0];
    }
  }

       最终，pieccewise jerk完成了求解，后面的To jerk函数在这里就不过多介绍了，主要原理就是利用积分，最终得到整条横向位移（沿着s轴），然后通过frenet转化，从而得到笛卡尔坐标系下的具体路径。 由此完成了轨迹规划中的路径规划。

       关于路径规划部分的代码已单独上传到git，链接如下：path_planning