MPSK通信系统的设计与性能研究-8PSK

文章和代码已经归档至【Github仓库：communication-system-simulation】或者公众号【AIShareLab】回复 通信系统仿真 也可获取。

一、8PSK背景

略

二、原理概述

2.1 PSK调制

发送端发送的是一连串离散而随机的二进制比特流，使用PSK载波相位调制的方法，这样发送端发送的消息便包含在了相位中，此种调制方法可以十分有效地节约带宽。

$$u_m(t)=A{g}_T(t)\cos (2\pi f_{c}t+\frac{2\pi m}{M}),m=0,1,\dots ,M-1$$

其中, $g_T(t)$ 是发送滤波器的脉冲形状, 传输信号的频谱特性由它决定。A则是信号的幅度。在 $\mathrm{psk}$ 调制中, 所有的 $\mathrm{psk}$ 信号对于所有的 $\mathrm{m}$ 都具有相同的能量。
能量为:

$${\epsilon }_m={\int }_{-\infty }^{+\infty }{u}_m^2(t)dt={\epsilon }_s{\epsilon }_s$$
代表每个传输符号的能量。

在本次实验中, 为了方便分析, 我们令 $\mathrm{A}=1,g_T(t)=\sqrt{\frac{2{\epsilon }_s}{T}},0\le t\le T$ , 那么, 相应的 $\mathrm{gsk}$ 调制信号的波形为

$$\begin{array}{l}{u}_m(t)=\sqrt{\frac{2{\epsilon }_s}{T}}\cos (2\pi f_{c}t+\frac{2\pi m}{M})=\sqrt{\frac{2{\epsilon }_s}{T}}(A_{mc}\cos 2\pi f_{c}t-A_{ms}\cos 2\pi f_{c}t),m=0,1,\dots ,M-1,0\le t\le T\end{array}$$

我们规定:

$$\begin{array}{l}{A}_{mc}=\cos \frac{2\pi m}{M}{A}_{ms}=\sin \frac{2\pi m}{M}\end{array},m=0,1,\dots ,M-1.$$

经过上述分析, 我们不难得出, 这样一个相位调制信号可以看作两个正交载波, 因

此, 数字相位调制信号可以在几何上可用二维向量的形式来表示, 即

$$\vec{s}\ast m=(\sqrt{\epsilon \ast s}\cos \frac{2\pi m}{M},\sqrt{{\epsilon }_s}\sin \frac{2\pi m}{M})$$

正交基函数为:

$$\begin{array}{l}{\psi }_1(t)=g_T(t)\cos 2\pi f_{c}t{\psi }_2(t)=-g_T(t)\sin 2\pi f_{c}t\end{array}.$$

2.2 信号传输

调制信号在 AWGN 信道传输的时候, 会有噪声混杂进来, 此时输出信号变为: $$r(t)=u_m(t)+n_c(t)\cos (2\pi f_{c}t)-n_s(t)\sin (2\pi f_{c}t)$$

其中, $n_c(t)$ 和 $n_s(t)$ 分别是加性噪声的同相分量和正交分量, 之后, 我们将输出信号和 给出的基函数作相关, 则两个相关器的输出为: $r=s_m+n=(\sqrt{{\epsilon }_s}\cos \frac{2\pi m}{M}+n_c,\sqrt{{\epsilon }_s}\sin \frac{2\pi m}{M}+n_s)$ 需要注意的是 $n_c(t)$ 和 $n_s(t)$ 这两个正交噪声的分量是零均值, 互不相关的高斯随机过程。

2.3 解调方式

（1）最小欧式距离准则判决

最小欧式距离准则判决: 求出接收到的信号向量与 M 个传输向量的欧式距离, 选取 对应的最小欧式距离的向量, 该向量对应的符号即为判决输出符号。此种方法需要掌握 距离度量的概念并熟练运用, 下面给出关于距离度量具体的

理论分析:

在接收消息尚不确定 (即还没有接收到矢量 $\vec{r}$ ) 的情况下, 要使得先验概率为最大, 最好的判决方法就是选择具有最高先验概率 $P({\vec{s}}_m)$ 的信号; 接受到矢量 $\vec{r}$ 后, 其方法与 前者类似, 前者是寻找先验概率的最大值, 此时是寻找后验概率的最大值, 换言之, 选择使 $P({\vec{s}}_m\mid \vec{r})$ 最大的 ${\vec{s}}_m$ , 这个判决准则称为最大后验概率 (MAP) 准则。

根据贝叶斯公式, 后验概率可表示为: $P(\vec{s}\ast m\mid \vec{r})=\frac{f(\vec{r}\mid \vec{s}\ast m)P(\vec{s}\ast m)}{f(\vec{r})}$ 当 M 个信号先验概率相等, 由于 $f(\vec{r})$ 和 $P(\vec{s}\ast m)$ 均为确定的值 $(P(\vec{s}\ast m)=\frac{1}{M})$ 。则寻找 $P(\vec{s}\ast m\mid \vec{r})$ 的最大值就等价于寻找 $f(\vec{r}\mid {\vec{s}}_m)$ 的最大值。此时 MAP 准则简化为 ML 准则。

我们不妨对接收到的矢量 $\vec{r}$ 进行简要的分析, $\vec{r}={\vec{s}}_m+\vec{n}$, ${\vec{s}}_m$ 是信号矢量, $\vec{n}$ 是 AWGN 信道中的噪声矢量, 噪声矢量的分量 $n_k$ 服从分布 $N(0,\frac{N_o}{2})$ , 则 $r_k$ 服从分布 $N(s_{mk},\frac{N_0}{2})$

因此

$$\begin{array}{rlr}f(\vec{r}\mid \vec{s}\ast m)& =\prod \ast {k=1}^N\frac{1}{\sqrt{\pi N_0}}{\mathrm{e}}^{-\frac{(r_k-s_{mk}{)}^2}{N_0}}& =\frac{1}{(\pi N_0{)}^{\frac{N}{2}}}{e}^{\frac{|\vec{r}-\vec{s}\ast m{|}^2}{N\ast 0}},m=1,2,\dots ,M\end{array}$$

右端取对数有:

$\ln f(\vec{r}\mid \vec{s}\ast m)=-\frac{N}{2}\ln (\pi N\ast 0)-\frac{1}{N_0}{\sum }_{k=1}^N(r_k-s_{mk}{)}^2$

上式若要取得最大值, 显而易见 ${\sum }_{k=1}^N(r_k-s_{mk}{)}^2$ 需要取最小值。这也是符合我们直观印象的, 信号空间里两个信号点的欧氏距离越小, 说明它们越接近。

因此, 定义距离度量 $D(\vec{r}\mid {\vec{s}}_m)$

如下:
$$D(\vec{r}\mid \vec{s}\ast m)=\sum \ast {k=1}^N(r_k-s_{mk}{)}^2,m=1,2,\dots ,M$$

(2) 最佳检测器

最佳检测器将收到的信号向量 r 投射到 M 个可能的传输信号向量 { s m } \{s_{m}\} { sm​} 之一上去, 并 选取对应与最大投影的向量。将上述定义的距离度量展开:

$$D(\vec{r}\mid \vec{s}\ast m)=|\vec{r}{|}^2-2\vec{r}\cdot \vec{s}\ast m+|\vec{s}\ast m{|}^2,m=1,2,\dots ,M$$

其中, $|\vec{r}{|}^2$项对所有的判决度量是等价的的, 我们忽略这一项, 则得到相关度量:

$$C(\vec{r}\mid \vec{s}\ast m)=2\vec{r}\cdot \vec{s}\ast m-|\vec{s}\ast m{|}^2,m=1,2,\dots ,M$$

可以看出, 距离度量越小, 则相关度量越大。

上述分析也证明了老师要求证明的内容：即相关度量与距离度量是完全等价的。

2.4 错误概率

理论错误概率：

8PSK: $\mathrm{erfc}(\sqrt{3\times 10^{\frac{SNR}{10}}}\times \sin (\frac{\pi }{8}))$ ;

QPSK: $\mathrm{erfc}(\sqrt{10^{\frac{SNR}{10}}})\times (1-0.25\times \mathrm{erfc}\sqrt{10^{\frac{SNR}{10}}})$

实际错误概率:

误码率: 错误码元/传输总码元

误比特率: 错误比特/传输总比特

三、系统框图

8PSK:

图3.1 8PSK系统框图

四、主函数设计

4.1 星座图绘制主函数

1.流程图

图4.1 星座图绘制主函数流程图

2.代码实现

clc,clear,close;
% Symbol sequence length
L=100000;
% Generate the original bit sequence
sourceSeq=randnum(L);
[pI,pQ,sourceSeqCode]=Map(sourceSeq,L);
Eb = 1/3;

errbit = zeros(1,26);
errnum = zeros(1,26);
SNR=-5:20;
LS = length(SNR);
for i=1:LS
    % Find the one-sided power spectral density of noise for a given signal-to-noise ratio
    N0=Eb/(10^(SNR(i)/10)); 
    % variance
    var(i)=N0/2  ;      
    [rI,rQ]=noise(var(i),pI,pQ);
    [result,I]=judgment(rI,rQ);
    [errbit(i),errnum(i)]=Count(result,I,sourceSeq,sourceSeqCode);
end
draw(sourceSeqCode,rI,rQ);

4.2 QPSK与8PSK误码率对比主函数

1.流程图

图4.2 qpsk与8psk误码率对比主函数流程图

2.代码实现

clc,clear,close;
% Symbol sequence length
L=100000;
% Generate the original bit sequence
sourceSeq=randnum(L);
[pI,pQ,sourceSeqCode]=Map(sourceSeq,L);
Eb = 1/3;

errbit = zeros(1,26);
errnum = zeros(1,26);
SNR=-5:20;
LS = length(SNR);
for i=1:LS
    % Find the one-sided power spectral density of noise for a given signal-to-noise ratio
    N0=Eb/(10^(SNR(i)/10)); 
    % variance
    var(i)=N0/2  ;      
    [rI,rQ]=noise(var(i),pI,pQ);
    [result,I]=judgment(rI,rQ);
    [errbit(i),errnum(i)]=Count(result,I,sourceSeq,sourceSeqCode);
end
% draw(sourceSeqCode,rI,rQ);

% Calculate the theoretical bit error rate using the erfc function
Theory8PSKSER = erfc(sqrt(3*10.^(SNR/10)) * sin(pi/8)); 
% QPSK 
TheoryQPSKSER = erfc(sqrt(10.^(SNR/10))).*(1-0.25*erfc(sqrt(10.^(SNR/10))));;
% Load the SER-SNR curve of QPSK
load('qpsk_errnum');
figure(2);
epskerr = errnum/L;
semilogy(SNR,epskerr,'r-o');hold on;
semilogy(SNR,qpskerr,'b-o');hold on;
semilogy(SNR,Theory8PSKSER,'k-');hold on;
semilogy(SNR,TheoryQPSKSER,'k-');hold on;
ylabel('SER');
xlabel('SNR/dB')
legend('8PSK仿真曲线','QPSK仿真曲线','理论曲线','Location', 'northeast' );
grid on;
axis([-5,20,10e-7,1]);

五、子函数设计

5.1 随机比特序列的产生

代码实现：

function [SourceSeq]=randnum(L)
% L is the length of the generated sequence code
% Since a code is composed of 3 bits, it is generated here with 3*L.
randnum=rand(3*L,1);
% Initialize the original sequence
SourceSeq=zeros(3*L,1);
% The randomly generated sequence is judged
% if the random number is greater than 0.5, it is judged as 1, otherwise it is judged as 0.
for i=1:3*L
    if(randnum(i)>=0.5)
        SourceSeq(i)=1;
    else
        SourceSeq(i)=0;
    end
end

5.2格雷编码序列

代码实现

% Define 8psk mapping function
function [pI,pQ,SourceCode] = Map(SourceSeq,L)
% pI - in-phase component
% pQ - quadrature component
% SourceCode - The size of the binary number of each digit of the sequence
% initialization
pI = zeros(L,1);
pQ = zeros(L,1);
% In order to facilitate subsequent expressions, sqrt(2)/2 is represented here
root =sqrt(2)/2;
% Constructing the mapping matrix according to the Gray code of 8PSK
MappingMat = [[1,0];[root,root];[-root,root];[0,1];[root,-root];[0,-1];[-1,0];[-root,-root]];

SourceCode =zeros(L,1);
% mapping process
for i=1:L
    % Since a source symbol is composed of three bits
    % the low and high bits are read in reverse order here, and expressed in decimal
    SourceCode(i)=SourceSeq(3*i-2)*4+SourceSeq(3*i-1)*2+SourceSeq(3*i)+1;
    % Find the corresponding code through the decimal representation and map it
    pI(i) = MappingMat(SourceCode(i),1);
    pQ(i) = MappingMat(SourceCode(i),2);
end
end

% Octal Gray Code Conversion
function[a1,a2]=Map_other(N)
% a1 is a sequence of random bits in binary
% a2 is a sequence of octal symbols
% Random bit sequence of length 3L
a1=bit(3*N);
% a2 is used to store the code element sequence of length L
a2=zeros(1,N);
for i=1:3:3*N-2
   a2((i+2)/3)=abs(a1(i)*7-abs(a1(i+1)*3-a1(i+2)));
% Converts binary bit sequence Gray-encoded to octal sequence
end 
end

5.3 映射函数

代码实现

% 8PSK coordinate mapping
function [y3]=coordinate(x1,bit)
% x1 is the encoded octal sequence, bit is the originally generated binary random sequence
N=length(x1);
Es=bit*bit'/N;
% The first line of y3 is used to store the abscissa
% the second line is used to store the ordinate
y3=zeros(2,N);
% Coordinate mapping
for i=1:N
    y3(1,i)=sqrt(Es)*cos(pi/4*x1(i)+pi/8);
    y3(2,i)=sqrt(Es)*sin(pi/4*x1(i)+pi/8);
end
end

5.4 噪声生成与叠加输出

代码实现

% Generate Gaussian random noise sub-function , var is the variance
function [rI,rQ] = noise(var,pI,pQ)
L = length(pI);
nc=zeros(L,1);
ns=zeros(L,1);
for k=1:L
u=rand;
z=sqrt(var*2*log(1/(1-u)));
nc(k)=z*cos(2*pi*u);
ns(k)=z*sin(2*pi*u);
end
% Output two mutually orthogonal Gaussian signals
rI = pI+nc;
rQ = pQ+ns;
end

5.5 判决函数

代码实现

% Judgment Criterion: Minimum Euclidean Distance Criterion
function [result,I]=judgment(rI,rQ)
root=sqrt(2)/2;
L = length(rI);
I=zeros(L,1);
mapl = [[1,0];[root,root];[-root,root];[0,1];[root,-root];[0,-1];[-1,0];[-root,-root]];
for i=1:L
    index=0;
    minp=100;
    for j=1:8
        % Traverse each coordinate
        % find the point with the smallest Euclidean distance from the point, and record it.
        if((mapl(j,1)-rI(i))^2+(mapl(j,2)-rQ(i))^2<minp)
            minp=(mapl(j,1)-rI(i))^2+(mapl(j,2)-rQ(i))^2;
            index=j;
        end
    end
    I(i)=index;
end

% According to the judgment point, make the corresponding assignment
result = zeros(3*L,1);
for i=1:L
    switch(I(i))
        case 1
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(0,0,0);
        case 2
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(0,0,1);
        case 3
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(0,1,0);
        case 4
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(0,1,1);
        case 5
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(1,0,0);
        case 6
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(1,0,1);
        case 7
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(1,1,0);
        case 8
            [result(3*i-2),result(3*i-1),result(3*i)]=SetValue(1,1,1);
    end
end

end

SetValue将对应的值进行赋值即可，由于判决函数中调用次数过多，因此抽象封装成一个函数，便于使用。

% SetValue function
function [a,b,c]=SetValue(d,e,f)
a=d;
b=e;
c=f;
end

5.6星座图绘制函数

代码实现

function draw(I,rI,rQ)
figure;
root = sqrt(2)/2;
%映射矩阵
MappingMat = [[1,0];[root,root];[-root,root];[0,1];[root,-root];[0,-1];[-1,0];[-root,-root]];
L=length(I)
for i=1:L
    % Draw points with different colors according to different values
    switch(I(i))
        case 1
            plot(rI(i),rQ(i),'*','color','r');hold on;

        case 2
            plot(rI(i),rQ(i),'*','color','g');hold on;

        case 3
            plot(rI(i),rQ(i),'*','color','b');hold on;

        case 4
            plot(rI(i),rQ(i),'*','color','c');hold on;

        case 5
            plot(rI(i),rQ(i),'*','color','m');hold on;

        case 6
            plot(rI(i),rQ(i),'*','color','y');hold on;

        case 7
            plot(rI(i),rQ(i),'*','color','k');hold on;

        case 8
            plot(rI(i),rQ(i),'*','color','[0.5,0.5,0.5]');hold on;

    end
end
x = -4:0.1:4;
y = -2:0.1:2;
% plot(x,zeros(length(x)),'k');hold on;
% plot(zeros(length(y)),y,'k');hold on;
axis equal
axis([-2,2,-2,2]);
end

5.7误码率及误比特率计算函数

代码实现

function [errbit,errsymbol]=Count(result,I,sourceSeq,sourceSym)
% result: the sequence after the decision
% I: symbol after decision
% sourceSeq: original bit sequence
% sourceSym: original symbol sequence
errbit=0;
errsymbol=0;
for i=1:length(sourceSeq)
    if(sourceSeq(i)~=result(i))
        errbit=errbit+1;
    end
end
for i=1:length(I)
    if(I(i)~=sourceSym(i))
        errsymbol=errsymbol+1;
    end
end
end

六、性能分析与实验结果

6.1 比较8PSK与QPSK的Monte Carlo仿真误符号率曲线、理论误符号率曲线差别

在AWGN信道下，未加信道纠错码的8PSK调制通信系统检测器的判决准则选为最小距离法（星座图上符号间的距离），格雷码映射，比较数据点为100000时8PSK与QPSK的Monte Carlo仿真误符号率曲线，理论误符号率曲线，比较差别（横坐标是SNR=Eb/N0）。(一张图上呈现4条曲线)

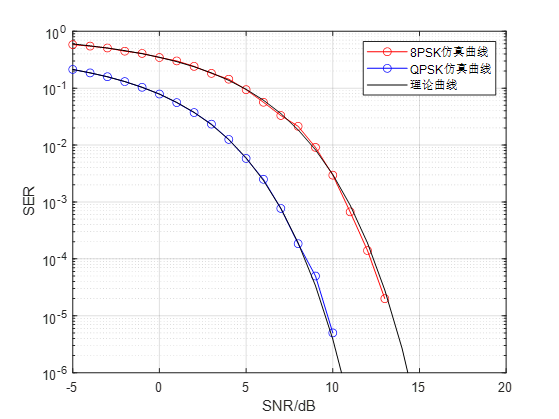
图6. 1 QPSK与8PSK性能比较

通过Monte Carlo仿真误符号率曲线可以看出，整体仿真结果基本符合理论计算曲线，并且在不同的信噪比下，对应的QPSK的误码率明显小于8PSK的误码率，8PSK的星座图如下：

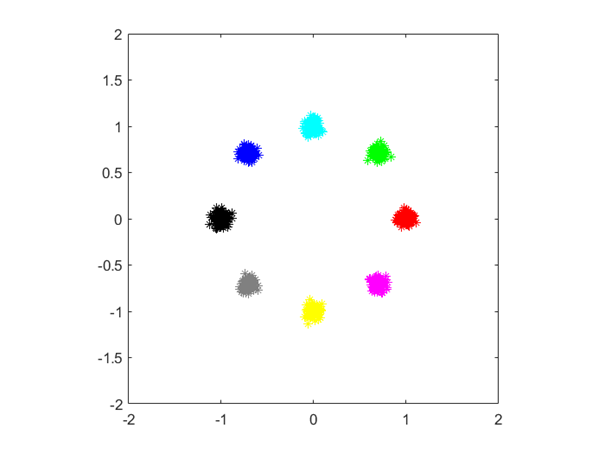
图6. 2 8PSK星座图

6.2 理论分析8PSK性能比QPSK

理论证明如下：

$$\begin{array}{l}{r}_{o1}=\sqrt{\frac{{\epsilon }_g}{2}}\cos (\frac{2\pi m}{M})+n=\sqrt{{\epsilon }_s}\cos (\frac{2\pi m}{M})+n_c{r}_{o2}=\sqrt{\frac{{\epsilon }_g}{2}}\sin (\frac{2\pi m}{M})+n=\sqrt{{\epsilon }_s}\sin (\frac{2\pi m}{M})+n_s\end{array}$$

假设发送信号的相位为 $\theta =0$ ，那么

$$r_{o1}=\sqrt{{\epsilon }_s}+n_c{r}_{o2}=n_s$$

因为 $n_c$ 和 $n_s$ 是联合高斯随机过程
$$f_r(r_{o1},r_{o2})=\frac{1}{2\pi {\sigma }_r^2}\exp (-\frac{(r_{o1}-\sqrt{{\epsilon }_s}{)}^2+r_{o2}^2}{2{\sigma }_r^2})$$

检测的测度为相位 ${\Theta }_r={\tan }^{-1}(r_{o2}/r_{o2})$

$$f_{{\Theta }_r}({\theta }_r)=\frac{1}{2\pi }{e}^{-2{\rho }_s{\sin }^2{\theta }_r}{\int }_0^{\infty }v{e}^{-(v-\sqrt{4{\rho }_s}\cos {\theta }_r{)}^2/2}dv$$

其中 ${\rho }_s={\epsilon }_s/N_0$ . $\mathrm{v}$ 是接收矢量 $\mathrm{r}$ 的包络. 若 ${\rho }_s>>1$ 且 $|{\Theta }_r|<=\pi /2$

$f_{{\Theta }_r}({\theta }_r)\approx \sqrt{\frac{2{\rho }_s}{\pi }}\cos {\theta }_r{e}^{-2{\rho }_s{\sin }^2{\theta }_r}$ 若发送相位 0 , 当噪声使接收矢量的相位落在区域 $-\pi /M<{\Theta }_r<\pi /M$ 之外时会发生判 决错误，即

$$\begin{array}{c}{P}_e=1-{\int }_{-\pi /M}^{\pi /M}{f}_{{\Theta }_r}({\theta }_r)d\Theta \approx 1-{\int }_{-\pi /M}^{\pi /M}\sqrt{\frac{2{\rho }_s}{\pi }}\cos {\theta }_r{e}^{-2{\rho }_s{\sin }^2{\theta }_r}d{\theta }_r\approx 2Q(\sqrt{2{\rho }_s}\sin \frac{\pi }{M})=2Q(\sqrt{2{\log }_{2}M{\rho }_b}\sin \frac{\pi }{M})\end{array}$$

对于 M=4 ， 码元错误概率应为:

$$P_4=1-(1-P_2{)}^2=2Q(\sqrt{\frac{2{\epsilon }_b}{N_0}})[1-\frac{1}{2}Q(\sqrt{\frac{2{\epsilon }_b}{N_0}})]$$

对于 M=8 , 码元错误概率为:

$$P_8=2Q(\sqrt{2\frac{({\log }_{2}8)E_b}{N_0}}\sin \frac{\pi }{8})$$

很明显, 随着 $\mathrm{M}$ 的不断增长, $\mathrm{Pe}$ 也在不断增加。符合实验结果。

七、问题回顾与总结

1.对二进制序列格雷编码的问题

针对二进制序列格雷编码，主要有两种思路，分别是直接法和间接法，直接法是先根据8PSK的格雷码构造映射矩阵，根据该3bit数表示码元的十进制值寻找其在格雷码矩阵中的对应位置，并且进行映射，需要注意的部分是由于一个源码元是由三个bit组成的，因此实际读取中，以3位单位进行遍历，并且通过倒序的方式读取低高位。

2.关于MPSK误符号率的问题

最开始计算误符号率时, 对于 QPSK 的理论误码率, 我最开始采用的是 MPSK 的统一公式:

$$\begin{array}{c}{P}_{s,MPSK}=2Q(\sqrt{2\frac{E_s}{N_0}}\sin \frac{\pi }{M})=2Q(\sqrt{2\frac{k{E}_b}{N_0}}\sin \frac{\pi }{M})=2Q(\sqrt{2\frac{({\log }_{2}M)E_b}{N_0}}\sin \frac{\pi }{M})\end{array}$$

但是在后续的学习中, 才发现上述公式尽可以在 M>4 的情况下才可以使用, 而对于 \mathrm{M}=4 时的系统误码率, 应该采用公式:

$$\begin{array}{cc}{P}_4& =1-P_e=2Q(\sqrt{\frac{2{\epsilon }_s}{N_0}})[1-\frac{1}{2}Q(\sqrt{\frac{2{\epsilon }_b}{N_0}})]\end{array}$$

3.关于星座图绘制的问题

在绘制星座图时，初步想法是对于每一个判决分类的样本点采用不同的颜色绘制，但是对于如何针对点进行颜色，线性的绘制，我的初步想法是建立一个颜色-线性的向量，然后对于每个点判决的具体情况找到对应的样本颜色线型，采用数组引用的形式进行属性的赋值，但是随后发现看似简化了绘制过程，实际却在引用时产生很大的工作量，还可能产生错误绘制，因此综合比较下我选择用switch的方法进行情况判断，并对相应的判决点进行绘制。