二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
减而治之,通过不断缩小搜索区间的范围,直到找到目标元素。如:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
public static int search(int[] nums, int target) {
int start = 0;
int end = nums.length - 1;
int mid;
while (start <= end) {
//折半查找
mid = (start + end) / 2;
if (target > nums[mid]) {
start = mid + 1;
} else if (target < nums[mid]) {
end = mid - 1;
} else {
return mid;
}
}
return -1;//找不到返回-1
}
一个栗子
题目描述: 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。
示例:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
这次就牛逼了,一次通过,因为我之前写过的归并排序算法就用到了。
解题思路
看到这个题目,我的第一思路就是:合并2个数组(归并),然后在判断是奇数项还是偶数项来取值,代码如下:
public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
//定义一个空数组来合并2个数组的集合
int len = nums1.length + nums2.length;
int[] nums = new int[len];
//i代表nums1的索引,j代表nums2的索引
for (int index = 0, i = 0, j = 0; index < len; index++) {
if (i >= nums1.length) {
//说明nums1的数据已经取完,直接取nums2中的数据
nums[index] = nums2[j++];
} else if (j >= nums2.length) {
//说明nums2的数据已经取完,直接取nums1中的数据
nums[index] = nums1[i++];
} else if (nums1[i] > nums2[j]) {
nums[index] = nums2[j++];
} else {
nums[index] = nums1[i++];
}
}
//合并之后判断新数组是奇数项还是偶数项
if (len % 2 == 1) {
//如果是奇数项
return Double.valueOf(nums[len / 2]);
} else {
//偶数项
Double d = Double.valueOf(nums[(len / 2) - 1] + nums[(len / 2)]);
return d / 2;
}
}
通过是通过了,但题目说:你能设计一个时间复杂度为 O(log(m+n)) 的算法解决此问题吗?这也是为什么二分查找那么多例子我却举了这个,因为相对来说是比较难的一个二分查找了,主要是应用思想比较难理解。
上面的解法,假设两个数组的长度分别为m,n,很显然,时间复杂度为O(m+n),因为用了一个新数组来合并之前的2个数组,所以空间复杂度也为O(m+n)。
那么怎么做到时间复杂度为 O(log(m+n))呢?如果对时间复杂度的要求有 log,通常都需要用到二分查找,这道题也可以通过二分查找实现,但是需要转换一下思路(官方和精选解法三,自己记录总结一下)。
假设两个有序数组分别是A和B。根据中位数的定义,当 m+n 是奇数时,中位数是两个有序数组中的第 (m+n)/2 个元素,当 m+n是偶数时,中位数是两个有序数组中的第 (m+n)/2 个元素和第 (m+n)/2+1 个元素的平均值。因此,这道题可以转化成寻找两个有序数组中的第 k 小的数,其中 k 的值为(m+n)/2 或 (m+n)/2+1。
这就好理解了,由于数列是有序的,其实我们完全可以一半一半的排除。假设我们要找第 k 小数,我们可以每次循环排除掉 k/2 个数,我们来看下面这个例子:要找第 7 小的数字
第一种情况:A[k/2] > B[k/2]

我们继续比较两个数组的第 k/2 个数(这个过程就是递归),如果 k 是奇数,向下取整。
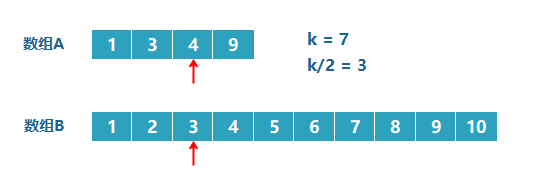
即上图中是比较数组 A 的第3个数和数组 B 的第3个数,比较发现A[3]{4} > B[3]{3}(这里[]中的值不是表示索引,而是表示第几个数,{}中的值表示第几个数对应的值),这也就说明数组 B 的前 3( 1、2、3 )个数不可能是第7小的数字,即哪个小,就表明该数组的前 k/2 个数字都不是第 k 小数字,可以排除。
怎么理解?我们是把 k 拆分到2个数组的,即每个数组有 k/2 个数,合起来也就是k/2 + k/2 = k个数,那么
- 对于A数组,比
A[k/2]小的数,去掉它自己,那就是k/2-1个。 - 对于B数组,比
B[k/2]小的数,去掉它自己,那就是k/2-1个。 - 如果
A[k/2]比B[k/2]前面的数大,B[k/2]前面的数就是第k/2-1,那总的来说比A[k/2]小的数最多就是(k/2-1)+(k/2-1) = k-2个,再加上B[k/2]这个数,那就是A[k/2]最多是第k-1小的数,而比A[k/2]小的数更不可能是第k小的数了,所以可以把它们排除。
在结合上面的例子,数组A[k/2]的值4大于数组B[k/2]的值3,所以总的比4小的值包括A(1、3)自己的加上B(1、2、3)的为5个,也就是k-2=7-2=5,所以我们可以把B中的前k/2个数排除掉。剩下就是1,3,4,9 和 4,5,6,7,8,9,10 两个数组作为新的数组进行比较。

第二种情况:A[k/2] < B[k/2]
同理,B[k/2] 都比 A[k/2] 前面的数大,就排除A数组前 k/2 个数字,由于我们已经排除掉了 3 个数字,就是这 3 个数字一定在最前边,所以在两个新数组1,3,4,9 和 4,5,6,7,8,9,10中,我们只需要找第k-(k/2),即 7-3=4 小的数字就可以了,也就是 k = 4 。此时两个数组,比较第 2 个数字,3 < 5,所以我们可以把小的那个数组中的 1,3 排除掉。
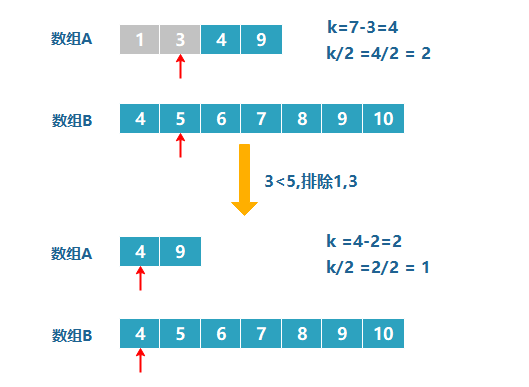
注:这里有个点,为什么下次 k 的值为k-(k/2)?既然排除了数组B的前3个数,那么对于新数组不就应该继续是二分k=(m+n)/2吗?(PS:这种想法很正常,我开始也是这么想的)
我们回到问题的起始点,求两个正序数组的中位数,实际我们把它转为了求一个正序数组的第 k 小的数,如对于正序数组[1,3,5,7,9,10,11,12,20],如果我们要找到第 5小的数,那其实就是找在第 5 个位置的数,就是 9,也就是说我们要找的这个数是 9 。如果我们删除掉数组最前面的三个数那就变成[7,9,10,11,12,20],这时我们继续要找到 9 这个数,那 9 所在的位置是不是就变成了第 2(5-3=2)个位置了。对应到上图中的排除的前3个数,需要注意的是这里的排除并不是从数组中删除这3个数,只是在下次运算不计在内而已,也就是说对于求第k小的数这个值是不变的(就对应 9 不变),也就是中位数这个值不变,这就很好的说明了为什么下次k的值为k-(k/2)而不是k=(m+n)/2。
第三种情况:A[k/2] = B[k/2]
当我们继续往下分的时候,出现了这样一种情况,就是两个数组对应位置上的值相等。
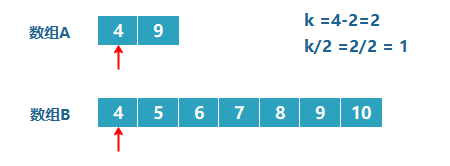
如上图,4 == 4 ,这怎么处理呢?由于两个数相等,所以我们无论去掉哪个数组中的都行,因为去掉 1 个总会保留 1 个的,所以没有影响。为了统一,我们就假设A[4]>B[4],所以此时将数组B中的 4 去掉。
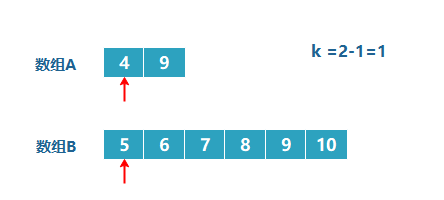
此时发现 k=1了,也就是我们要找数组中第 1 小的数字,那第一小不就是数组的第一个数吗?但是我们这是2个分开的数组,并没有合并(但是你可以在心里假设如果是合并的话,怎么处理,那必然是谁小谁就排在前面),所以我们只需要判断两个数组中第 1 个数字哪个小就可以了,也就是 4 。
所以我们得出结论,对于数组1,3,4,9 和 1,2,3,4,5,6,7,8,9,10的中位数为 4。
特殊情况
上面的例子是比较理想化的例子,但实际可能有很多情况,因为我们每次都是取 k/2 的数进行比较,有时候可能会遇到数组长度小于 k/2 的时候,这就是数组的边界问题。如下:
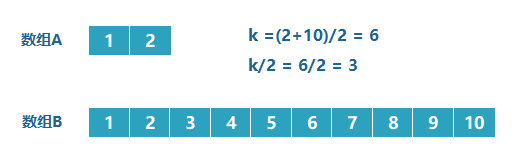
此时 k/2=3 ,而A数组的长度为 2 ,我们此时将箭头指向它的末尾就可以了。这样的话,由于 2<3 ,所以就会导致上边的数组 1,2 都被排除。
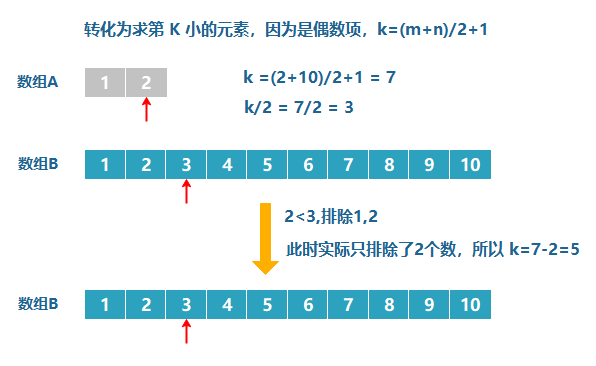
由于 2 个元素被排除,所以此时 k=5 ,又由于A数组已全部排除,所以我们只需要返回B数组的第 5 个数字就可以了。
看到这,有人说了:第 5 个数不是 5 吗?,那中位数不是应该是(4+5)/2=4.5才对吗?这个我们去代码里面把奇数和偶数的情况中和不就完事了吗?
从上边可以看到,无论是找第奇数个还是第偶数个数字,对我们的算法并没有影响,而且在算法进行中,k 的值都有可能从奇数变为偶数,最终都会变为 1 或者一个数组空,直接返回结果。
所以我们采用递归的思路,为了防止数组长度小于 k/2 ,所以每次比较 min(k/2,len(数组)) 对应的数字,把小的那个对应的数组的数字排除,将两个新数组进入递归,并且 k 要减去排除的数字的个数。**递归出口就是当 k=1 或者其中一个数组长度是 0 **。
代码实现
讲了思路,那下一步就是写代码了,其实很多人都能理解思路,真到去写代码的时候却无从下手,我也一样,写了几次总是会出现 bug,主要原因就是我们在写代码的时候没有把分析的思路带进去,因此针对上面存在的情况,实际上在代码中我们可以把它分为2种即可:
-
正常情况,即递归到
k=1的时候按照上面的分析,
k=1的时候,我们始终要记得我们求的是第 k 小的数,对于一个数组,k=1就是对于这个数组的第一个位置的数,对于 2 个分开的数组,那就是要比较 2 个数组的第一个位置的大小,且取小的那个。 -
边界情况,数组为空
什么时候数组会为空,以上面特殊情况为例,必定是数组的长度短的那个,但是到底是哪一个数组的长度短,我们只需要根据两个数组的长度去判断一下即可,如上面的数组
A[1,2]和数组B[1,2,3,4,5,6,7,8,9,10]。如果我们反过来A是A[1,2,3,4,5,6,7,8,9,10],B是B[1,2],这个时候我们若仍要短的那个数组在前面,那是不是可以把 B 和 A 换个位置即可。这样我们在代码中就不需要去判断到底是 A 数组会为空还是 B 数组会为空。
好了,开始写代码了,还有个注意的点,就是第k个元素,那么对应的索引应该是k-1,这就是细节,不然迟早越界。
public static double findMedianSortedArrays2(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
int total = m + n;
//如果是奇数项,刚好中间那个值就是中位数
if (total % 2 == 1) {
return getKthElement(nums1, 0, nums2, 0, (total / 2 + 1));
} else {
//当为偶数项时,中位数是两个有序数组中的第 (m+n)/2个元素和第 (m+n)/2-1 个元素的平均值,所以我们查找2次即可
Double d = Double.valueOf(getKthElement(nums1, 0, nums2, 0, total / 2) + getKthElement(nums1, 0, nums2, 0, (total / 2) + 1));
return d / 2;
}
}
/**
* @param A 数组A
* @param startA 数组A的排除位置,索引值0开始
* @param B 数组B
* @param startB
* @param k 第k小的数
*/
public static int getKthElement(int[] A, int startA, int[] B, int startB, int k) {
//lenA和lenB表示的是假删除后的数组长度
int lenA = A.length - startA;
int lenB = B.length - startB;
//1.数组为空的情况,先比较两个数组的长度,
if (lenA > lenB) {
//如果A>B交换位置,保证B始终是最长的那个
return getKthElement(B, startB, A, startA, k);
}
//为空的情况
if (lenA == 0) {
return B[startB + k - 1];
}
//2.k=1的情况
if (k == 1) {
return Math.min(A[startA], B[startB]);
}
//3.正常情况,k还不等于1的时候,取k/2的值比较
//对于A数组,如果递归n次之后,假如排除了startA个元素后,同时需要考虑数组是否到达边界,若到达边界就取数组的最后一个元素即可
int i = startA + Math.min(lenA, k / 2) - 1;
//同理,B数组的取值也一样
int j = startB + Math.min(lenB, k / 2) - 1;
//然后,在判断
if (A[i] > B[j]) {
//如果这时A>B的值,则B排除前k个元素,则B下次的起始位置就是j+1
return getKthElement(A, startA, B, j + 1, k - (j - startB + 1));
} else {
return getKthElement(A, i + 1, B, startB, k - (i - startA + 1));
}
}
代码中在去下个k的值是这么取的,乍一看,真看不懂

但你把这段代码带进去,替换i和j的值

比如带入j的值就是:
k-(j-startB+1) = k-(startB+Math.min(lenB, k / 2)-1-startB + 1) = k-(Math.min(lenB, k / 2));
Math.min(lenB, k / 2)是什么?不就是k/2吗?边界情况就是lenB。
另外,在精选解法第三种解法中,是把奇偶情况合并了,即:

怎么理解?
- 假如
n=3,m=4,就有left=4,right=4,一共7个数最后返回刚好第四个数(一样的数相加再除以2); - 假如
n=4,m=6,就有left=5,right=6,一共10个数返回第五第六个数的均值,然后就不用管奇偶了。
时间复杂度
每进行一次循环,我们就减少 k/2 个元素,所以时间复杂度是 O(logk),而 k = (m+n)/2 ,所以最终的复杂也就是 O(log(m+n))。