基于python语言利用割线法原理求解函数最小值问题

解题思路 定义一个范围和初始点X0，X1

当其迭代公式导数足够小时，我们可以认为此刻的导数已经非常接近于0，为极值点

此时停止循环，得出X代入方程为极小值

割线法的迭代公式：

、

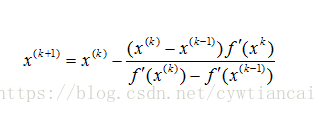
import numpy as np
from sympy import *



eps=0.001

def minGX(f,x0,x1):
    x=Symbol('x')
    k=0
    D=1
    while D>eps:
        
        dfx1=diff(f,x).subs('x',x1)
        dfx0=diff(f,x).subs('x',x0)
        x2=x1-(x1-x0)*dfx1/(dfx1-dfx0)
        k=k+1
        D=abs(dfx1)
        x0=x1
        x1=x2
    
    print(f.subs('x',x2))