一、什么是堆?
堆(Heap)是一种特殊的完全二叉树,满足性质:除叶节点外每个节点的值都大于等于(或者小于等于)其孩子节点的值(该性质又称「堆序性」)。
堆有两种类型:
- 大根堆(又称最大堆):堆中每一个节点的值都大于等于其孩子节点的值。所以大根堆的特点是堆顶元素(根节点)是堆中的最大值;
- 小根堆(又称最小堆):堆中每一个节点的值都小于等于其孩子节点的值。所以小根堆的特点是堆顶元素(根节点)是堆中的最小值。
下图展示了大根堆与小根堆的区别:

二、堆的实现
堆通常用数组来实现(数组名一般为 h h h,即heap的首字母)。具体来讲,我们从 1 1 1 开始,按照层序遍历的顺序给每个节点进行编号,例如,对于上图中的大根堆而言,其编号顺序如下:
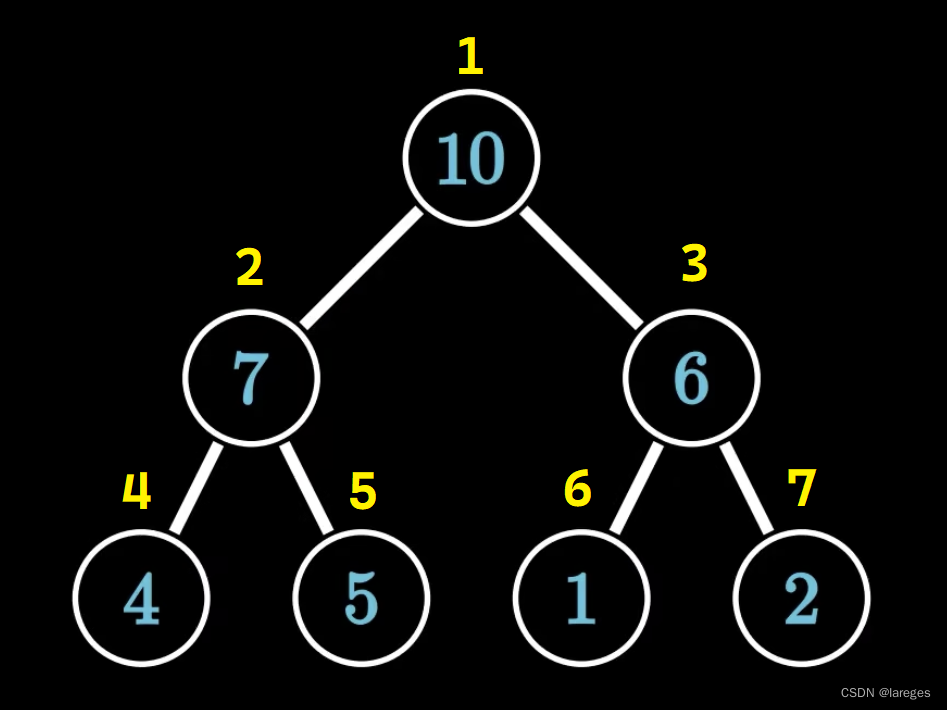
每个节点的编号就是该节点在数组中的下标,相应的数组为 h [ ] = { 0 , 10 , 7 , 6 , 4 , 5 , 1 , 2 } h[\;]=\{0,10,7,6,4,5,1,2\} h[]={ 0,10,7,6,4,5,1,2}(第 0 0 0 个元素是什么不重要)。
按照这种编号方式,不难发现:
- 根节点的编号一定是 1 1 1;
- 若一个节点的编号为 x x x,则它左子节点(如果有)的编号为 2 x 2x 2x,右子节点(如果有)的编号为 2 x + 1 2x+1 2x+1;
- 若一个节点的编号为 x x x,则它父节点(如果有)的编号为 x / 2 x/2 x/2(这里的除法是整除)。
此外,根据完全二叉树的性质,还可以得到:
- 若堆中含有 n n n 个元素,则堆的高度为 ⌊ log 2 n ⌋ + 1 \lfloor\log_2 n\rfloor+1 ⌊log2n⌋+1;
- 若一个节点的编号为 x x x 且满足 x > n / 2 x>n/2 x>n/2(这里的除法是整除),则该节点一定是叶子节点,否则是分支节点。
2.1 上滤与下滤
⚠️ 为统一起见,接下来提到的堆均指小根堆。
上滤(又称向上调整)和下滤(又称向下调整)是堆的两种基本操作。
上滤是指将不符合堆序性的某个元素向上调整至合适的位置,下滤是指将不符合堆序性的某个元素向下调整至合适的位置。
先来看下滤操作是如何进行的。设编号为 x x x 的节点不满足堆序性(该节点一定不是叶子节点,否则讨论将变得毫无意义),接下来分两种情况考虑:
- 编号为 2 x 2x 2x 的节点存在,编号为 2 x + 1 2x+1 2x+1 的节点不存在: 这时候一定成立 h [ x ] > h [ 2 x ] h[x]>h[2x] h[x]>h[2x],此时交换 h [ x ] h[x] h[x] 和 h [ 2 x ] h[2x] h[2x] 即可;
- 编号为 2 x 2x 2x 的节点和编号为 2 x + 1 2x+1 2x+1 的节点均存在: 这时候 h [ x ] > h [ 2 x ] h[x]>h[2x] h[x]>h[2x] 和 h [ x ] > h [ 2 x + 1 ] h[x]>h[2x+1] h[x]>h[2x+1] 中至少有一个成立。令 y = arg min { h [ 2 x ] , h [ 2 x + 1 ] } y=\argmin \{h[2x],\;h[2x+1]\} y=argmin{ h[2x],h[2x+1]},交换 h [ x ] h[x] h[x] 和 h [ y ] h[y] h[y] 即可。
下滤操作的实现:
void down(int x) {
while (x <= n / 2) {
// 当x不是叶子节点的时候持续向下调整
int y = 2 * x; // 如果x不是叶子节点,则至少存在左子节点
if (y + 1 <= n && h[y + 1] < h[y]) y++; // 判断左右子节点哪个更小,并令y等于更小的那个节点的编号
if (h[y] >= h[x]) break; // 如果左右子节点中的最小值都要大于等于节点x的值,说明x已经调整完毕
swap(h[x], h[y]), x = y; // 否则进行调整
}
}
比起下滤操作,上滤操作的实现更为简单(因为往下走有两种选择:左、右子节点,而往上走只有一种选择:父节点)。设编号为 x x x 的节点不满足堆序性(该节点一定不是根节点,否则讨论将变得毫无意义),则一定有 h [ x ] < h [ x / 2 ] h[x]<h[x/2] h[x]<h[x/2],不断交换 h [ x ] h[x] h[x] 和 h [ x / 2 ] h[x/2] h[x/2] 直至 h [ x ] ≥ h [ x / 2 ] h[x]\geq h[x/2] h[x]≥h[x/2] 即可。
上滤操作的实现:
void up(int x) {
while (x > 1 && h[x] < h[x / 2]) {
// 当x不是根节点的时候持续向上调整
swap(h[x], h[x / 2]);
x /= 2;
}
}
上滤操作和下滤操作的平均时间复杂度均为 O ( log n ) O(\log n) O(logn)。
2.2 堆的常用操作
仅用上滤和下滤我们就可以实现堆的常用操作:
| 操作 | 时间复杂度 |
|---|---|
| 获取堆顶元素的值 | O ( 1 ) O(1) O(1) |
| 向堆中插入一个元素 | O ( log n ) O(\log n) O(logn) |
| 删除堆顶元素 | O ( log n ) O(\log n) O(logn) |
| 删除堆中的任一元素 | O ( log n ) O(\log n) O(logn) |
| 修改堆中的任一元素 | O ( log n ) O(\log n) O(logn) |
通常,我们需要用两个变量来表示一个堆:一个是上文提到的 h h h 数组,另一个是 i d x idx idx,用来表示当前堆中有多少个元素。
操作一:获取堆顶元素的值
int top() {
return h[1];
}
操作二:向堆中插入一个元素
向堆中插入元素按照层序遍历的顺序进行,所以新插入的元素一定是叶子节点(编号最大的节点),此时对它进行上滤操作调整至合适的位置即可。
void push(int x) {
h[++idx] = x, up(x);
}
操作三:删除堆顶元素
做法是用堆中最后一个元素(即编号最大的元素)覆盖掉堆顶元素,然后删除最后一个元素,同时下滤堆顶元素。
void pop() {
h[1] = h[idx], idx--, down(1);
}
操作四:删除堆中的任一元素
不妨设要删除的元素的编号为 k k k,同样用最后一个元素覆盖掉这个元素,然后删除最后一个元素。此时对于编号为 k k k 的元素而言,要么执行上滤操作,要么执行下滤操作,要么什么都不用执行。简便起见,我们可以直接执行 down(k), up(k),这两个操作至多只有一个会被执行。
void pop(int k) {
h[k] = h[idx], idx--, down(k), up(k);
}
可以看出 pop(1) 与 pop() 等价。
操作五:修改堆中的任一元素
类似删除堆中的任一元素。
void modify(int k, int x) {
h[k] = x, down(k), up(k);
}
2.3 建堆
给定一个乱序数组 a a a,我们如何根据它来建堆呢?
如果对于每一个 a [ i ] a[i] a[i],依次调用堆的 push 方法,则总时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),有没有更好的方法呢?
考虑将 a a a 赋值给 h h h(事实上一般不会这么做,而是直接输入到 h h h),此时 h h h 所代表的仅仅是完全二叉树,因为 h h h 不一定满足堆序性。对该完全二叉树的每个分支节点进行下滤(因为下滤叶子节点无意义)即可得到堆:
void build() {
for (int i = idx / 2; i; i--) down(i);
}
下面分析 build 函数的时间复杂度。简便起见,不妨假设堆是满二叉树且含有 n n n 个元素,于是堆的高度为 h ≜ log 2 ( n + 1 ) h\triangleq\log_2(n+1) h≜log2(n+1)。规定根节点所在的层为第一层,于是最后一层的元素个数为 2 h − 1 2^{h-1} 2h−1,倒数第二层的元素个数为 2 h − 2 2^{h-2} 2h−2,以此类推。
build 从倒数第二层的节点开始逐个下滤,每个节点的操作次数至多是 1 1 1,因此 build 在倒数第二层的总操作次数为 2 h − 2 ⋅ 1 2^{h-2}\cdot 1 2h−2⋅1。
对于倒数第三层的节点,每个节点的操作次数至多是 2 2 2,因此 build 在倒数第三层的总操作次数为 2 h − 3 ⋅ 2 2^{h-3}\cdot 2 2h−3⋅2。
不断进行下去可得到 build 的总操作次数:
S = 2 h − 2 ⋅ 1 + 2 h − 3 ⋅ 2 + 2 h − 4 ⋅ 3 + ⋯ + 2 0 ⋅ ( h − 1 ) = ∑ i = 1 h − 1 i ⋅ 2 h − i − 1 \begin{aligned} S&=2^{h-2}\cdot 1+2^{h-3}\cdot 2+2^{h-4}\cdot 3+\cdots + 2^0\cdot (h-1)\\ &=\sum_{i=1}^{h-1}i\cdot 2^{h-i-1} \end{aligned} S=2h−2⋅1+2h−3⋅2+2h−4⋅3+⋯+20⋅(h−1)=i=1∑h−1i⋅2h−i−1
经过简单计算可得:
S = 2 S − S = ∑ i = 1 h − 1 i ⋅ 2 h − i − ∑ i = 1 h − 1 i ⋅ 2 h − i − 1 = ∑ i = 1 h − 2 2 h − i + 1 + 2 h + 1 − ( h − 1 ) = 2 h + 2 − h − 7 = O ( 2 h ) = O ( n ) \begin{aligned} S&=2S-S=\sum_{i=1}^{h-1}i\cdot 2^{h-i}-\sum_{i=1}^{h-1}i\cdot 2^{h-i-1} \\ &=\sum_{i=1}^{h-2}2^{h-i+1}+2^{h+1}-(h-1) \\ &=2^{h+2}-h-7\\ &=O(2^h)=O(n) \end{aligned} S=2S−S=i=1∑h−1i⋅2h−i−i=1∑h−1i⋅2h−i−1=i=1∑h−22h−i+1+2h+1−(h−1)=2h+2−h−7=O(2h)=O(n)
故建堆的时间复杂度为 O ( n ) O(n) O(n)。
三、堆排序
堆排序实际上就是先根据乱序序列建堆,然后将根节点与编号最大的节点进行交换(注意是交换而不是覆盖),同时下滤根节点。再将根节点与编号第二大的节点进行交换,同时下滤根节点,以此类推。
堆排序结束后,对堆进行层序遍历即可得到排序后的序列。
注意到如果初始时建立的是小根堆,则排序结束后会得到降序序列;如果初始时建立的是大根堆,则排序后会得到升序序列。
这里给出一个堆排序的模板:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n; // 堆中的元素数量
int h[N]; // 用于存储堆的数组
// 大根堆的下滤操作
void down(int x) {
while (x <= n / 2) {
int y = 2 * x;
if (y + 1 <= n && h[y + 1] > h[y]) y++;
if (h[y] <= h[x]) break;
swap(h[x], h[y]), x = y;
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> h[i]; // 读入乱序序列
for (int i = n / 2; i; i--) down(i); // 建立大根堆
int t = n; // 循环结束后n的值会变为0,所以需要先提前保存一下方便后续输出
while (n) {
swap(h[1], h[n]), n--, down(1);
}
for (int i = 1; i <= t; i++) cout << h[i] << ' '; // 输出升序序列
return 0;
}
容易看出堆排序的时间复杂度是 O ( n log n ) O(n\log n) O(nlogn),空间复杂度是 O ( 1 ) O(1) O(1)。
四、优先队列
所谓优先队列,就是指定队列中元素的优先级,优先级越大越优先出队,而普通队列则是按照进队的先后顺序出队,可以看成进队越早越优先。
STL中的优先队列实际上就是大根堆,元素越大越优先出队。本节主要讲解STL中的优先队列的用法。
使用优先队列需要先包含头文件:
#include <queue>
创建一个优先队列(大根堆):
priority_queue<int> q;
如果要创建一个小根堆,则可以这样声明:
priority_queue<int, vector<int>, greater<int>> q;
优先队列的常用操作:
| 操作 | 描述 |
|---|---|
q.top() |
返回队头元素 |
q.pop() |
弹出队头元素 |
q.push(x) |
向队列中插入元素 |
q.empty() |
判断队列是否为空 |
q.size() |
返回队列的大小 |
References
[1] https://oi-wiki.org/ds/heap/
[2] https://zh.cppreference.com/w/cpp/container/priority_queue
[3] https://zh.wikipedia.org/wiki/%E5%A0%86%E7%A9%8D
[4] https://www.acwing.com/activity/content/punch_the_clock/11/