模式识别 —— 第三章 非参数估计

模式识别 —— 第三章 非参数估计

概率密度的估计

我们以前在参数估计中都是先假设样本点的分布有一个概率密度函数形式，比如高斯分布，然后从样本中估计参数。但是，有可能样本点的分布根本不是高斯分布，那么我们的结果就错了。

本文提出的非参数法讲究不需要先假设样本服从一个什么分布，而是直接从样本中统计得到，比如频率分布直方图。

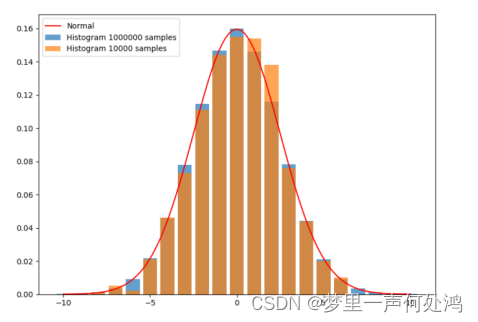
理论上，如果我们样本足够多，同时将频率分布直方图组距设置得特别小，组特别多，这就是在逼近样本点的真实概率密度函数。一般地，样本足够多的时候其可以表示出任意类型的分布！

概率
特征空间中一定区域内样本的比率 $$P={\int }_{R}p(x)\mathrm{d}x$$
这里其实就是对概率密度函数某一区域求积分，得到的值就是概率值。

概率密度
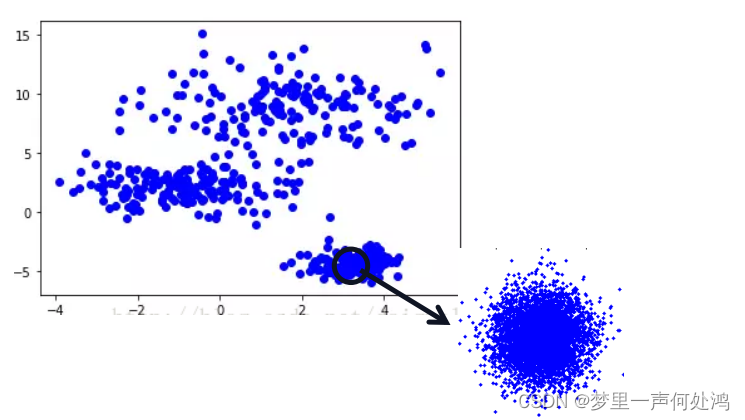如图如果某区域内点足够的多，并且我们划分的区域足够的小。那么我们可以大致认为该区域是等概率密度的。因此概率就等于概率密度乘以体积，如下式子：其中$n$是样本总数，$k$是某一区域内的样本点的个数
$${\int }_{R}p(x)\mathrm{d}x=\frac{k}{n}\approx p(x)V$$

因此：
$$p(x)\approx \frac{k/n}{V}$$

这里其实就是说每个区域要小，点数要多，n远多于k

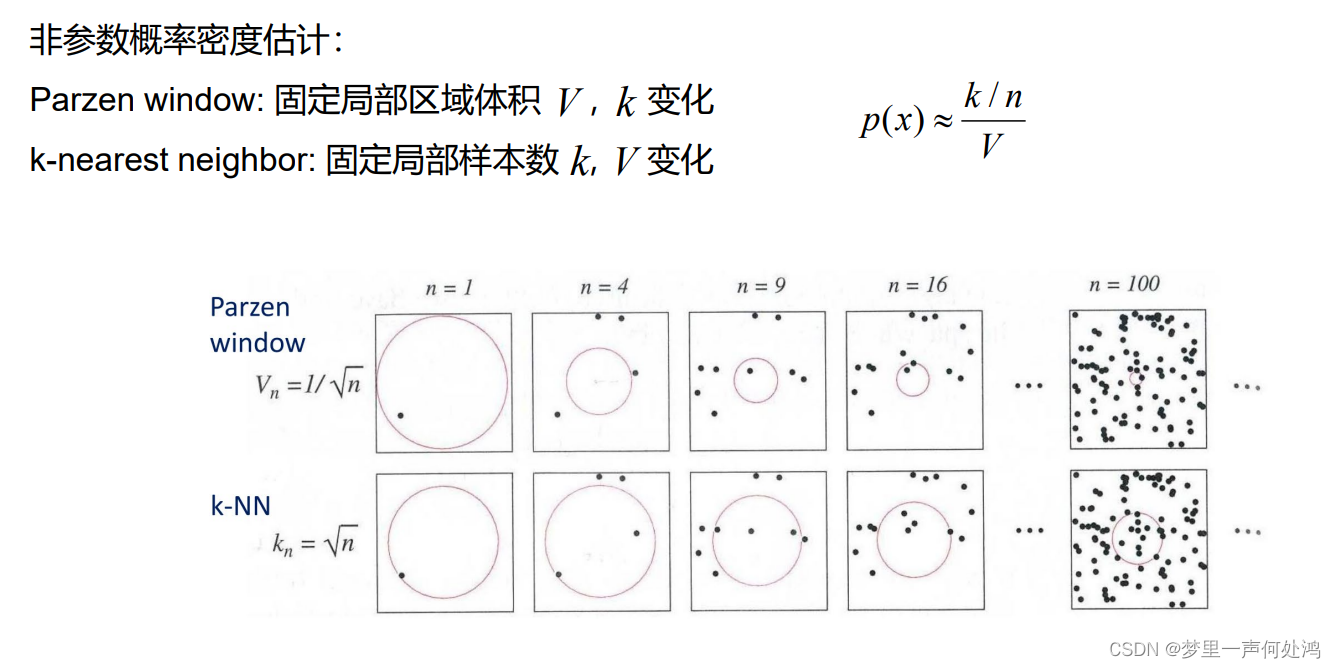
• 第一行是根据n算出体积后按照这个体积来看有多少个k落入其中
• 第二行是根据算出k后来改变V是的有k个样本落入其中

Parzen窗方法

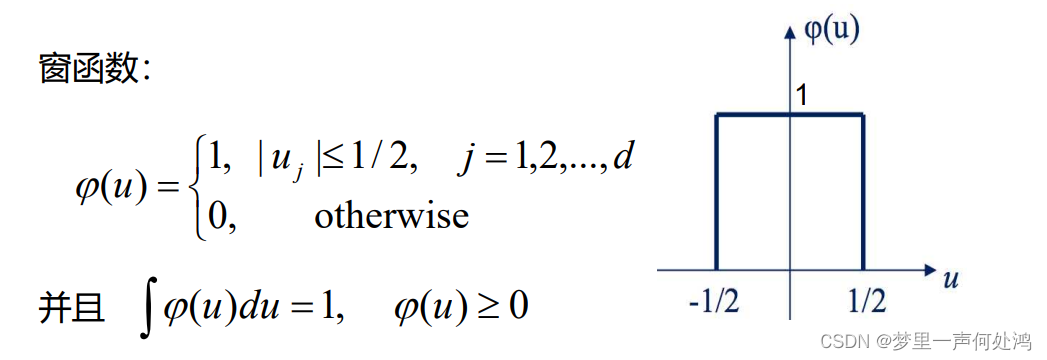
这个窗函数对于落在窗口内则函数值为1，否则为0。这个窗口在一维是一个关于原点对称的线段，长度为1；在二维是一个关于原点中心对称的正方形，面积为1；在三维是一个关于原点中心对称的正方体，体积为1。

扫描二维码关注公众号，回复： 14577878 查看本文章

推广：

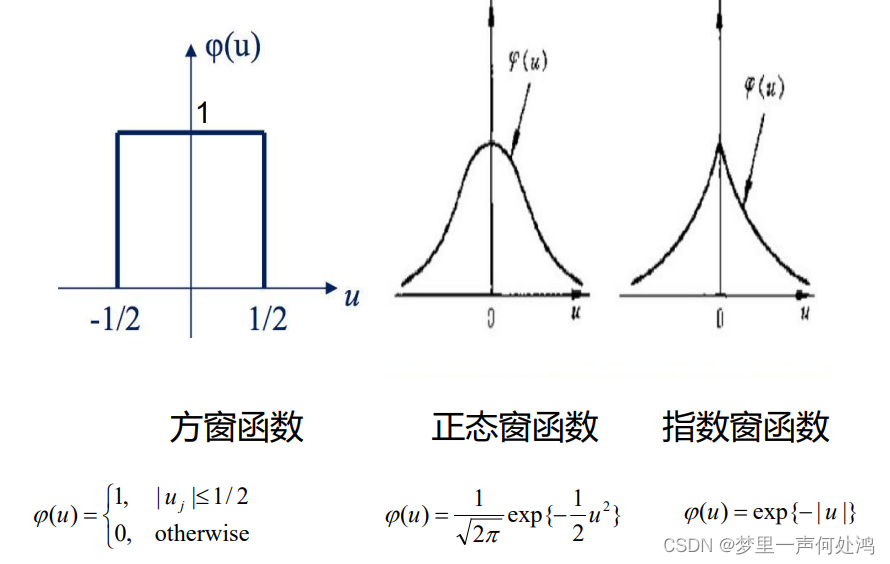
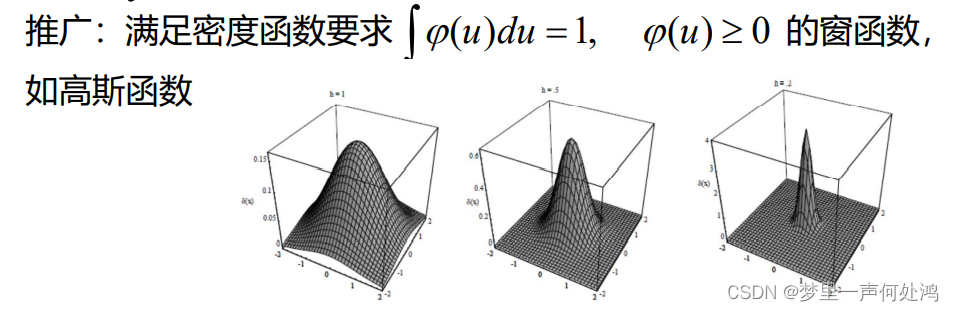
对于窗函数样本数和概率密度函数如下：

这里可以将$h_n$理解为单位长度，即对于任意一个样本点 $xi$ ，只要满足向量 $x-xi$​的某一个维度$\le \frac{h_n}{2}$，那么值为1（相当于计数器加1），这样可得到该区域的样本数。

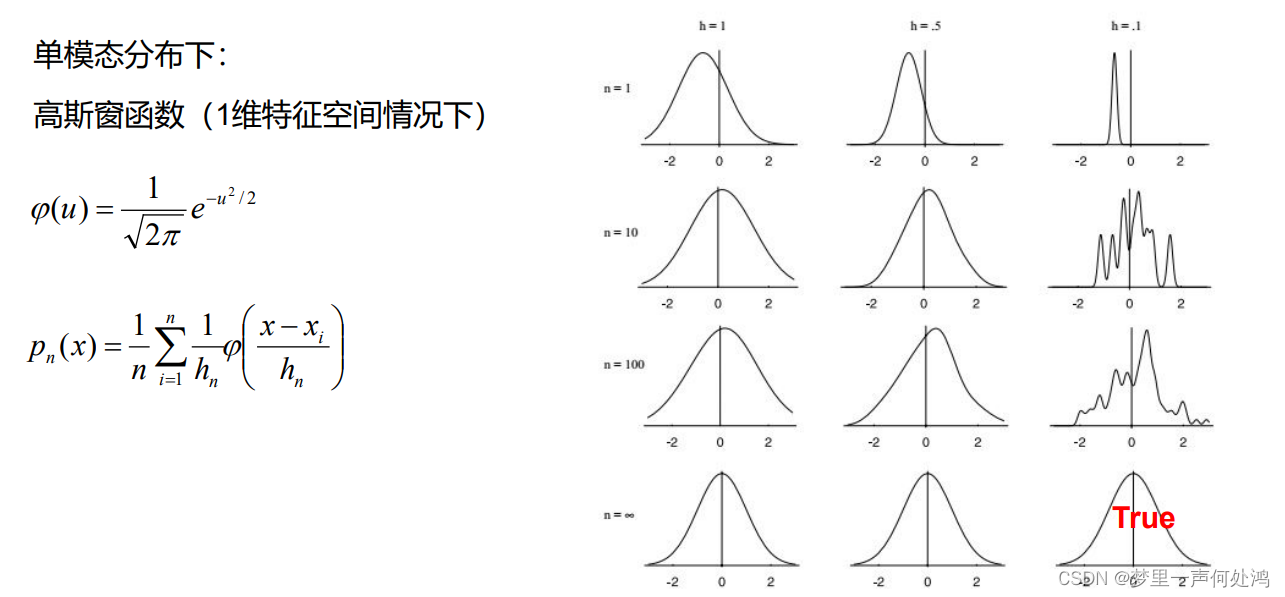如图可知，当h取值小时，函数曲线偏向细长。当样本n足够多的时候，窗口函数即可拟合出概率密度函数。

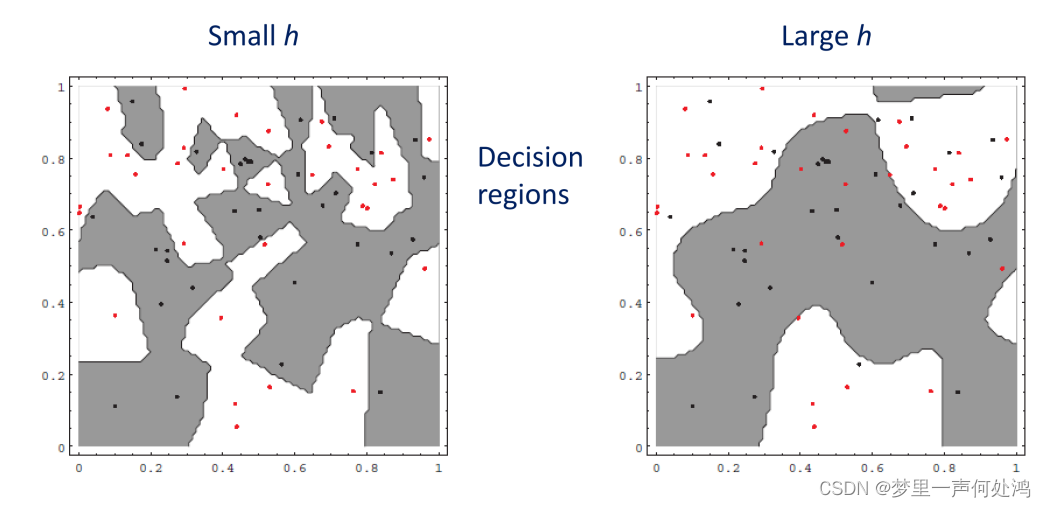
• 选取的H越小则$V_n$越小，统计的结果稳定性不够
• 选取的H越大则$V_n$越大，统计的结果分别率太低

K近邻估计

这种方法是固定局部区域样本数k，体积V变化。

对于k值的选择，这里采用$k_n=\sqrt{n}$

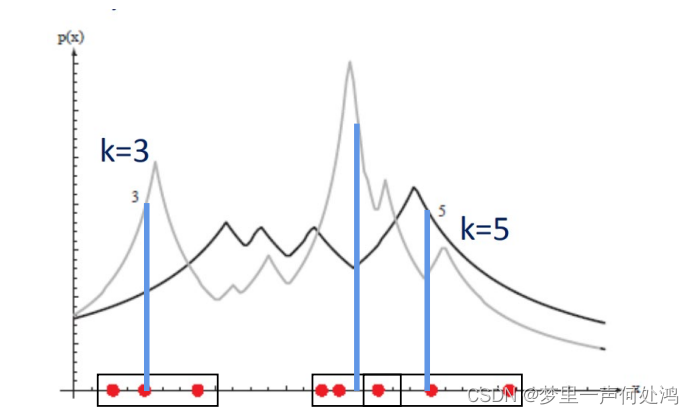
可见当k较小时，概率密度函数的曲线变化越剧烈。因为当k很小时，V很小且变化比较突兀。

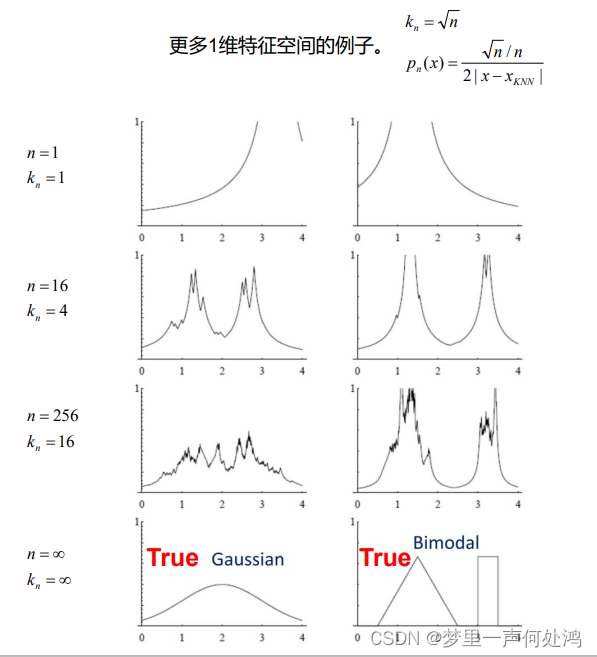
可见当n与k都趋近于无穷的时候，概率密度函数的曲线拟合的较好。

K近邻分类器

最近邻 (1-NN) 规则：在统计模式识别中，可以采用最小距离分类器，它是计算待分类的样本到各个已知类别的中心（通常是训练集中同类样本的重心）的距离，将其划分到距它最近的类别中心，这可以看作是一种最近邻的分类规则。

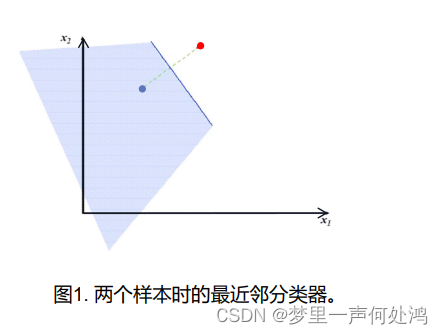例如，左边部分的点我们都将其归为蓝色；右边部分的点我们都将其归为红色。

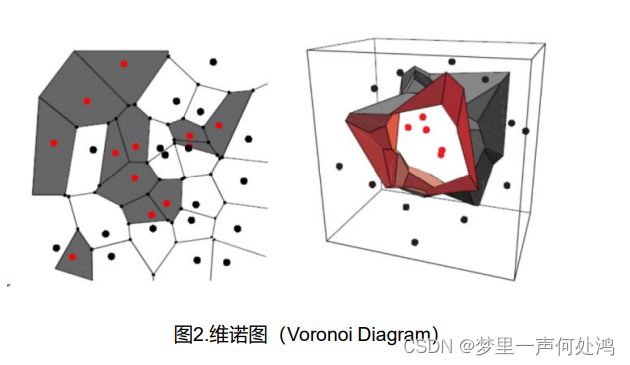
用此方法我们可以在样本点集中构建出上图。

K近邻的快速计算

k-近邻分类器原理简单，无需对样本集进行回归分析或者概率分布统计，实现起来十分方便。但是它有两个缺陷：

• 对于每一个待分类的样本，都必须计算到样本集中所有样本的距离，从而找出的 k 个近邻来完成分类，因此算法的计算量随着样本集的增大而增大；
• 样本集中的所有样本都必须被使用，这给算法带来了巨大的存储压力。为解决这两个问题，许多研究者对 k-近邻分类器进行了改进

有三种应对办法：

1. 部分距离
   

• 其实就是就是在计算过程中发现其距离已经大于已有的最小距离就不再继续计算了。

2. 预结构化
   - 其实就是将一些点看成一个整体，和这个整体的中心距离进行计算能够快速排除一些很远的点群。

3. 编辑
   
   删除被同类样本（Voronoineighbors）包围的原型

非参数估计和参数估计有联系但有很大区别，两者都非常重要。前者假定有一个概率密度函数形式，后者可以处理具有任意概率分布形式的数据。