[BZOJ1016][JSOI2008]最小生成树计数（辗转相除高斯消元+矩阵树定理）

题目：

我是超链接

题解：

最小生成树有两个性质：
(1)不同的最小生成树中,每种权值的边出现的个数是确定的
(2)不同的生成树中,某一种权值的边连接完成后,形成的联通块状态是一样的

那么我们其实可以把每种权值的处理看成是分开的好几步，然后根据乘法原理，将每一步得到的结果相乘。

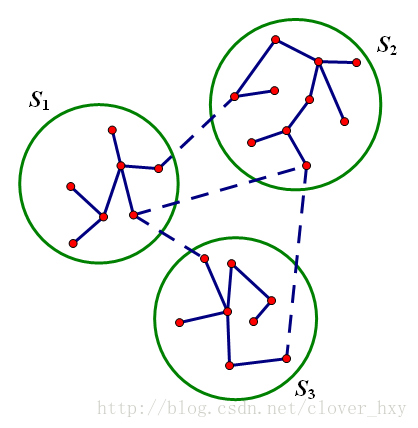
举个例子，下图中s1,s2,s3表示已经处理好的3个连通块，虚线表示一组同权值的边。加入这组边后s1,s2,s3可以连通。

将已经计算好的连通块缩成一个点，那么就变成了一个独立的图的生成树问题，可以用矩阵树定理求解。

引自blog

这里可以建立两个并查集，来维护last和目前的联通块，因为上一级已经成为联通块的状态不会使已经相连的点再连一遍，所以不用清空c数组即两点之间的边数

每次对于目前的每一个联通块，我们枚举里面的两个点构建K矩阵进行矩阵树定理，注意这里的矩阵树定理，有模数而且模数不是质数，我们要用【优化的高斯消元】，详见代码

代码：

#include <cmath>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int mod=31011;
const int N=1005;
vector <int> V[105];
int c[105][105],a[105][105],U[105],fa[105];bool vis[105];
struct hh{int x,y,z;}e[N];
int cmp(hh a,hh b){return a.z<b.z;}
int gauss(int n)
{
    for (int i=1;i<=n;i++)
      for (int j=1;j<=n;j++) a[i][j]%=mod;
    int ans=1;
    for (int i=1;i<=n;i++)
    {
        int num=i;
        for (int j=i+1;j<=n;j++)
          if (abs(a[num][i])<abs(a[j][i])) num=j;
        if (!a[num][i]) return 0;
        if (num!=i) for (int j=i;j<=n;j++) swap(a[num][j],a[i][j]);
        for (int j=i+1;j<=n;j++)
          while (a[j][i])
          {
            int t=a[j][i]/a[i][i];
            for (int k=i;k<=n;k++) a[j][k]=(a[j][k]-t*a[i][k])%mod;
            if (!a[j][i]) break;
            for (int k=i;k<=n;k++) swap(a[j][k],a[i][k]);
          }
        ans=a[i][i]*ans%mod;
    }
    return (abs(ans)%mod+mod)%mod;
}
int find(int x,int *f)
{
    if (x!=f[x]) return find(f[x],f);
    return x;
}
int main()
{
    int n,m,ans=1;scanf("%d%d",&n,&m);
    for (int i=1;i<=m;i++) scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z);
    sort(e+1,e+m+1,cmp);
    for (int i=1;i<=n;i++) fa[i]=i;
    for (int i=1;i<=m+1;i++)
    {
        if (e[i].z!=e[i-1].z || i==m+1)
        {
            for (int j=1;j<=n;j++)
              if (vis[j])
              {
                int f1=find(j,U);
                V[f1].push_back(j);
                vis[j]=0;
              }
            for (int j=1;j<=n;j++)
              if (V[j].size()>1)
              {
                memset(a,0,sizeof(a));
                int len=V[j].size();
                for (int k=0;k<len;k++)
                  for (int l=k+1;l<len;l++)
                  {
                    int x=V[j][k],y=V[j][l]; int t=c[x][y];
                    a[k+1][l+1]-=t; a[l+1][k+1]-=t;
                    a[k+1][k+1]+=t; a[l+1][l+1]+=t; 
                  }
                ans=ans*gauss(len-1)%mod;
                for (int k=0;k<len;k++) fa[V[j][k]]=j;
              }
            for (int j=1;j<=n;j++)
            {
                U[j]=fa[j]=find(j,fa);
                V[j].clear(); 
            }
        }
        int f1=find(e[i].x,fa),f2=find(e[i].y,fa);
        if (f1==f2) continue;
        U[find(f1,U)]=find(f2,U); vis[f1]=1; vis[f2]=1;
        c[f1][f2]++; c[f2][f1]++;
    }
    for (int i=2;i<=n;i++)
      if (find(i,fa)!=find(i-1,fa)) {ans=0;break;}
    printf("%d",(ans+mod)%mod);
}