混合策略改进的蝴蝶优化算法

文章目录

混合策略改进的蝴蝶优化算法

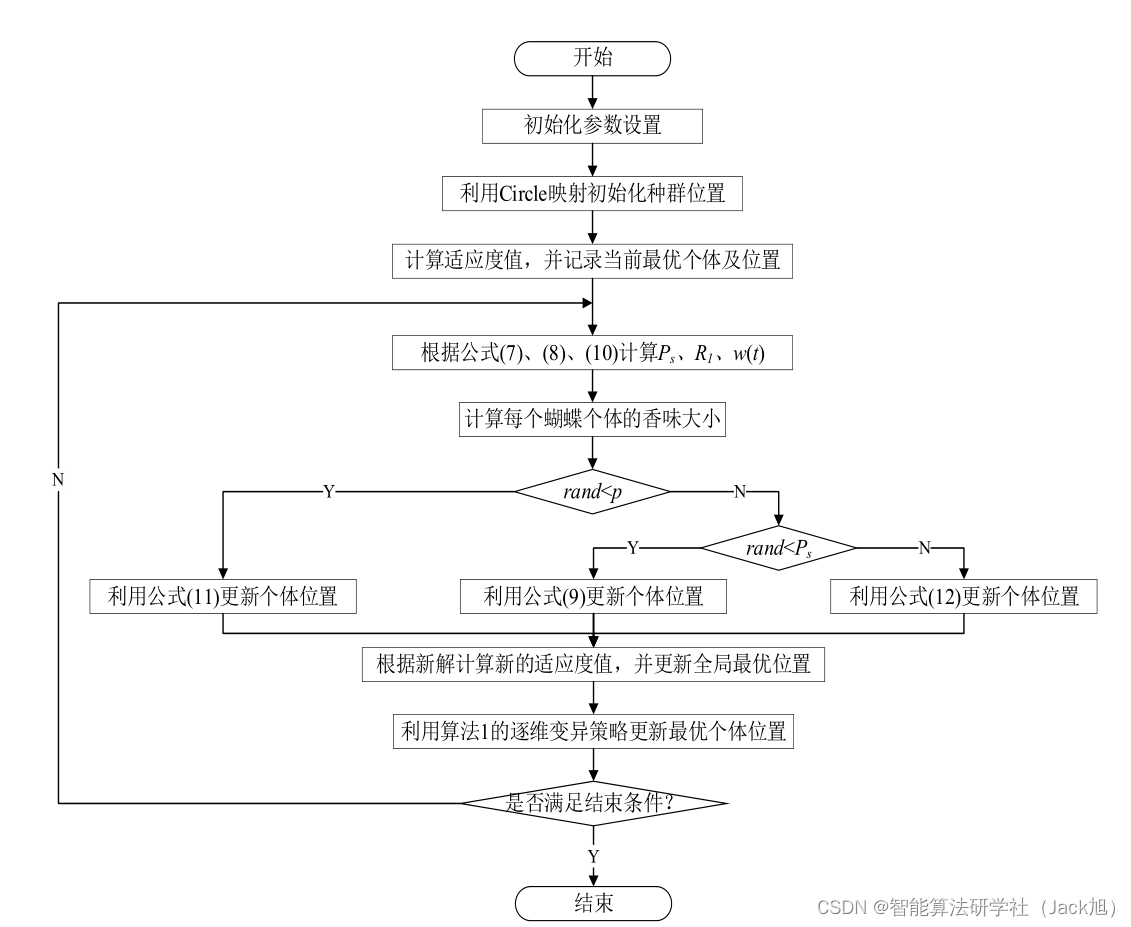
摘要：针对蝴蝶优化算法存在的求解精度低、易陷入局部最优等缺陷，提出混合策略改进的蝴蝶优化算法。首先，利用Circle映射初始化蝴蝶个体的位置，增加初始个体的多样性；其次，在局部搜索阶段利用动态切换概率控制改进正弦余弦算法与蝴蝶优化算法的转换，充分利用少量的蝴蝶个体，增强算法的局部开发能力；然后，在全局和局部位置更新处引入自适应余切权重系数，控制蝴蝶个体下一代的移动方向和距离，提高算法的收敛速度和精度；最后，引入逐维变异策略，对全局最优位置变异，引导种群向最优位置进化，避免陷入局部最优。

1.蝴蝶优化算法

基础蝴蝶优化算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107855860

2. 改进蝴蝶优化算法

2.1 混沌映射初始化

蝴蝶优化算法是在搜索空间中随机初始化种群的位置,
但是利用这种随机化方式生成初始种群, 有可能会导致蝴蝶个体的位置分布不均匀。考虑到混沌具有随机性、非周期性等特点, 可以利用混沌序列对蝴蝶个体位置进行初始化。目前存在多种不同的混沌映射 [14], 主要有 Logistic 映射、 Chebyshev 映射、Tent 映射、Circle 映射等。而利用 Circle 映射初始化种群的方法在智能优化算法中还很少被使用, 因此本文采用 Circle 映射初始化蝴蝶个体位置, 先利用 Circle 映射关系将变量映射到混沌变量空间内, 然后再将产生的混沌变量通过线性变换映射到需要优化的解空间, Circle 映射具体表达式如下：
$x_{i+1}=\bmod \left(x_{i}+0.2-(0.5 / 2 \pi) \sin \left(2 \pi x_{i}\right), 1\right) \tag{6}$
其中, $i$ 在本文中表示维度。

2.2 融合改进正弦余弦算法的局部搜索

$\mathrm{BOA}$ 算法在局部搜索过程中, 由于蝴蝶个体移动的范围较小, 容易陷入局部最优。而 $\mathrm{SCA}$ 算法具有较强的全局探测能力和局部开发能力, 因此在 BOA 算法的局部搜索阶段中融入 SCA 算法, 可以使局部搜索过程中少量的蝴蝶个体得到充分地利用, 并且指引蝴蝶个体向目标位置移动, 增强算法的局部开发能力。若切换概率设为常数, 不利于平衡 $\mathrm{SCA}$ 算法和 BOA 算法的局部开发能力, 因此本文利用一个随迭代次数自适应变化、函数范围变化较小、前期变化较慢后期变化较快的切换概率来控制在局部搜索阶段使用哪种位置更新方式, 在算法局部寻优的前期能够充分利用局部范围内的个体, 在局部寻优的后期能够快速地收玫到最优个体, 切换概率 $P_{s}$ 的计算公式如下:
$P_{s}=0.01 \times\left(\frac{t}{N_{-} i t e r}\right)^{3}+1 \tag{7}$
其中 $t 、 N_{-}$ iter 分别为当前迭代代数和最大迭代次数。当 rand $P_{s}$ 时, 算法采用正弦余弦算法进行位置更新操作, 反之, 算法采用 $\mathrm{BOA}$ 算法原来的局部位置更新公式, 这里的 rand 并不是 $[0, 1]$ 之间的随机数, 其范围为 $[1, 1.01]$ 。
由 $1.2$ 节可知, 在 SCA 算法中, 转换参数 $R_{1}$ 发挥着关键作用, 正弦与余弦的范围通过式(5)自适应的改变, 从而平衡算法的全局搜索和局部开采。但是这种线性递减的方式使算法容易陷入局部最优, 因此提出一种非线性单调递减的凸函数作为转换参数来更好地平衡全局搜索和局部开发。改进后的转换参数公式如下:
$R_{1}=\delta+\frac{b}{\exp \left(4 \times\left(\frac{t}{N_{-} \text {iter }}\right)^{4}\right)+1} \tag{8}$
其中 $b$ 为常数, 取值为 $\delta$ 为调节因子, 经过多次实验证明, 当 $\delta=0.95$ 时, 实验结果为最优。与式 $(5)$ 的线性递减方式不同, 式(8)在算法迭代前期 $R_{1}$ 下降缓慢, 可以更好地利用 $\mathrm{BOA}$ 算法局部搜索阶段的蝴蝶个体; 迭代后期 $R_{1}$ 下降快速, 可以指引蝴蝶个体尽快向目标值移动。改进后的正弦余弦算法位置更新公式如下:
$X_{i}^{d}(t+1)= \begin{cases}X_{i}^{d}(t)+R_{1} \times \sin \left(R_{2}\right) \times\left|R_{3} P_{*}^{d}(t)-X_{j}^{d}(t)\right| & R_{4}<0.5 \\ X_{i}^{d}(t)+R_{1} \times \cos \left(R_{2}\right) \times\left|R_{3} P_{*}^{d}(t)-X_{j}^{d}(t)\right| & R_{4} \geq 0.5\end{cases} \tag{9}$
其中 $X_{j}^{d}(t)$ 表示第 $t$ 次迭代中在种群内部随机选择的第 $j$ 个个体在第 $d$ 维上的解。

2.3 自适应权重系数

根据 BOA 算法原理可知, 蝴蝶个体利用当前位置和当前最优个体位置/随机蝴蝶个体位置来进行位置更新, 然而, 无论是在算法的全局搜索阶段还是局部搜索阶段, 这些个体的位置都没得到充分的利用。因此本文在 BOA 算法的全局搜索和局部搜索阶段共同引入一种随迭代次数变化的自适应权重 $w (t)$ , 使三种个体位置信息都能够得到充分地利用, 同时控制当前蝴蝶个体的移动方向和移动距离, 从而提高算法寻优精度和收敛速度。自适应权重 $w (t)$ 的数学表达式如下:
$w(t)=\alpha\left[\cosh \left(2 \times\left(1-\frac{10 t}{N_{-} \text {iter }}\right)^{4}\right)-1\right] \tag{10}$
其中, $\alpha \in[0,1]$ 。因此, BOA 算法引入自适应权重系数后全局搜索阶段的位置更新公式为
$x_{i}^{t+1}=w(t) \times\left(x_{i}^{t}+\left(r^{2} \times g^{*}-x_{i}^{t}\right) \times f_{i}\right) \tag{11}$
局部搜索阶段的位置更新为
$x_{i}^{t+1}=w(t) \times\left(x_{i}^{t}+\left(r^{2} \times x_{j}^{t}-x_{k}^{t}\right) \times f_{i}\right) \tag{12}$

2.4 逐维变异策略

BOA 算法同其他智能优化算法一样存在易陷入局部最优这一缺点, 经分析可知, 主要是由于算法没有充分利用最优个体的引导作用, 因此本文通过对最优个体进行变异, 提高种群多样性的同时指引种群向最优个体位置进化, 避免算法陷入局部最优。同时为了克服在高维情况下存在的维间干扰问题, 本文对最优个体位置采用逐维变异策略, 有效避免各维度之间信息的互相干扰。本文引入了文献 [15]中张超提出的 $\mathrm{t}$ -分布变异算子对最优个体位置进行扰动, 该 $\mathrm{t}$ -分布变异算子的自由度参数会跟随迭代次数的变化而变化, 逐维变异策略具体定义如下。
设搜索空间为 $d$ 维, 当前最优解 $g_{b e s t}=\left(g_{\text {best }}^{1}, g_{\text {best }}^{2}, \cdots, g_{\text {best }}^{d}\right)$ , 那么当前最优解逐维变异得到的新解 $g_{\text {new }}=\left(g_{n e w}^{1}, g_{\text {new }}^{2}, \cdots, g_{\text {new }}^{d}\right)$ 计算方式如下:
$g_{\text {new }}^{d}=g_{\text {best }}^{d}+T D(t)^{d} \times g_{\text {best }}^{d} \tag{13}$
其中 $t$ 为当前迭代次数, $T D (t)$ 是自由度参数为 $t$ 的 $\mathrm{t}$ -分布, $T D(t)^{d}$ 为 $\mathrm{t}-$ 分布在第 $d$ 维时生成的随机数。
因为无法直接判断变异后得到的新位置是否优于原位置, 所以本文利用了贪婪原则来判断是否接受新位置代替原最优位置。通过使用贪婪原则, 引导种群更好地向最优个体位置进化, 更好地提高算法的收敛速度。
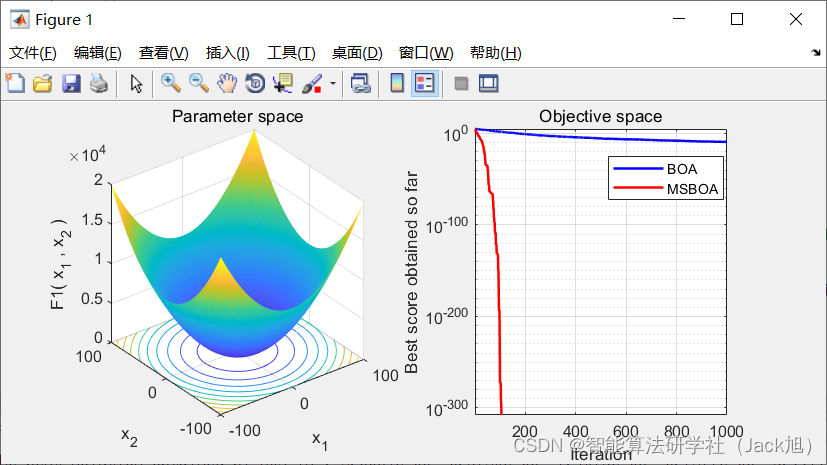
请添加图片描述

3.实验结果

请添加图片描述

4.参考文献

[1]宁杰琼,何庆.混合策略改进的蝴蝶优化算法[J/OL].计算机应用研究:1-7[2021-04-29].https://doi.org/10.19734/j.issn.1001-3695.2020.06.0171.