什么是红黑树
- 红黑树作为一种二叉搜索树,在于一些查找方面,红黑树能提高较高的查找效率。并且对比起AVL高度平衡二叉搜索树有着更少的旋转的特性,而更少的旋转能够带来更高的效率,所以C++的map/set底层,以及Linux的内核都倾向于使用红黑树。
- 红黑树的节点是由颜色来区分的,而这个颜色也正是红黑树能够减少旋转的一个重要因素。
红黑树的性质
-
- 每个结点不是红色就是黑色
-
- 根节点是黑色的
-
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
-
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
-
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
对于性质的分析,为何满足性质就能够减少旋转的次数,且能够保持最长的路径不会超过最短路径的两倍?
原因:
- 首先每条路径上的黑节点树要相同,那就意味着去除掉红节点,我们所看到一定是一颗满二叉树,
- 而红色节点必须父亲与左右节点都是黑色节点,这条性质保证了最长路径一定是黑红黑红…排列的而此时黑色节点和红色节点的数量是一致的。
- 而最短路径就是只出现黑色节点的路径,此时最长路径肯定最多是最短路径的两倍。
注意:这里的条件五叶子节点所指的是空节点,更准确地说是nil空节点,路径是以到nil叶子节点为止的。
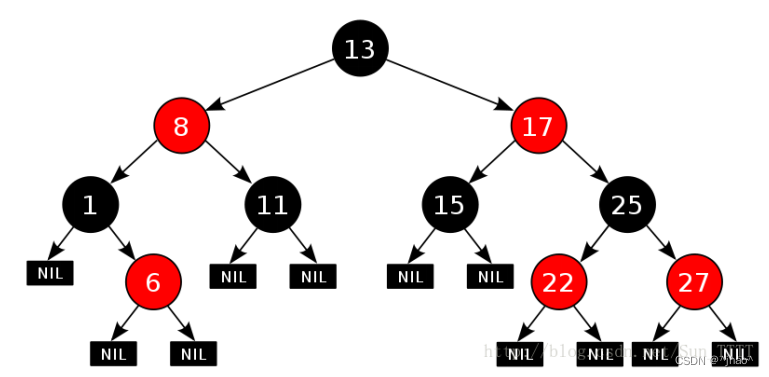
节点结构
节点采用三叉链,与保存的值,以及一个标识颜色的整形常数组成。(后面会更改)
enum Color
{
RED,
BLACK
};
template<class K,class V>
class RBTreeNode
{
public:
RBTreeNode(const pair<K,V>& kv)
:_col(RED)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
{
_kv = kv;
}
Color _col;
RBTreeNode<K,V>* _left;//左节点
RBTreeNode<K,V>* _right;//右节点
RBTreeNode<K,V>* _parent;//父节点
std::pair<K, V> _kv; //节点的值
};
节点插入的情况分析
首先需要解决一个问题,节点一开始给什么颜色呢?
给黑色的话会造成条件4不成立,需要对除添加节点所在路径以外的所有路径做修改,这未免也太麻烦了,所以我们采用的是插入红色节点,这样子最多破坏了规则三,而我们可以通过只修改当前路径的方式解决。
若插入的节点的父节点是黑色节点,就已经成功了,接下来考虑要变化的。
- 情况一:插入节点的叔叔节点为红
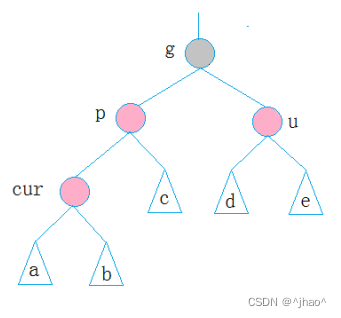
cur可能是由于下层的节点将黑色改成红色造成的,也有可能是新插入节点,为了解决这种情况,我们采用的方式是将p节点和u节点的颜色置成黑色,g节点置成红色,此时g就作为新插入的节点向上寻找。
if (uncle && uncle->_col == RED)
{
//情况一:优先判断,这种情况处理方式更简单
uncle->_col = parent->_col = BLACK;
g->_col = RED;
//向上迭代,此时g相当于新插入节点
//这个很重要
parent = g->_parent;
newNode = g;
continue;
}
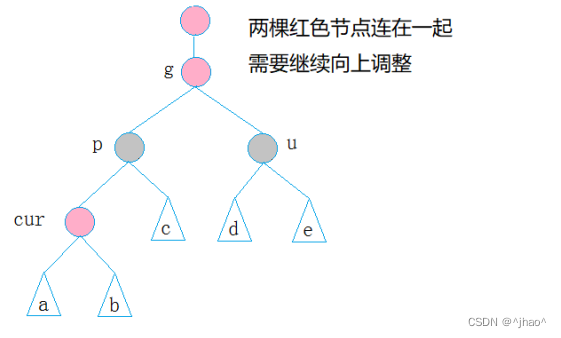
结束条件:

-
已经更新到根节点。
-
父节点是黑色的。
-
情况二:当uncle节点为NULL或者uncle节点不存在-
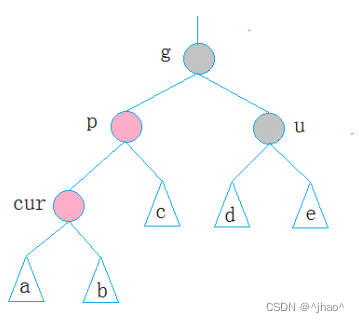
两种情况具体分析: -
uncle节点为黑的情况,一定是因为cur节点是新插入节点,否则cur所在路径上的黑色节点与u所在路径的黑色节点不相同,说明cur下的a,b节点各自有着黑色节点。
-
uncle不存在的情况则cur一定是新增节点,此时c,u,cur一定都是nil,随后cur插入进来。
解决方案:
旋转+更改颜色解决,由于路径上已经无法将红色节点处理了,原因就是红色节点所处的位置占据的不对,此时我们肯定不能删除红色节点,毕竟他保存着也是有效的数据。
此时将g节点作为分支中的一条,将底下的节点作为根,且置成黑色,既保证了每条路径的黑节点数量相同,也解决了红色节点与红色节点接触的问题。
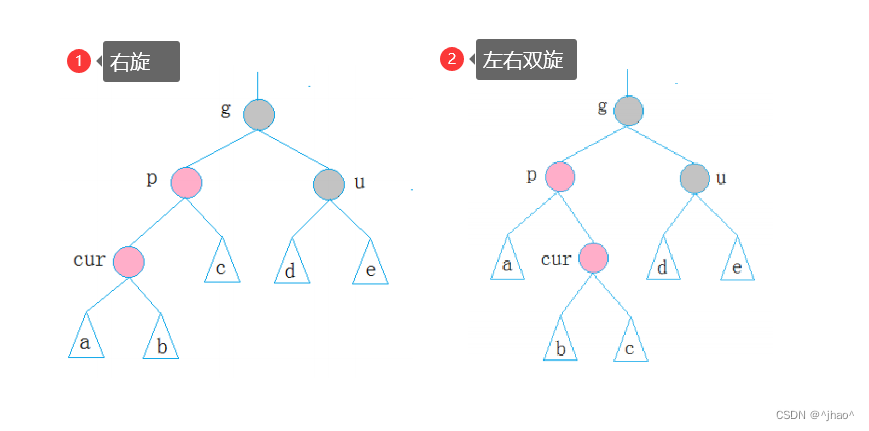
if (parent->_left == newNode)
{
//右单旋
RotateR(g);
parent->_col = BLACK;
g->_col = RED;
}
else
{
//左右双旋
RotateL(parent);
RotateR(g);
newNode->_col = BLACK;
g->_col = RED;
}
左旋和右左双旋同理。比起AVL的旋转,其实难度差不多。
红黑树的检验
- isRRTree函数证明是否有红色与红色节点相连接。
- RBDistance用于检测每条路径上的黑色节点数目是否相同。
- rbOrder用于检测节点中序遍历是否是有序的。
public:
bool IsRBTree()
{
bool rr = isRRTree(_head);
int beach = 0;
Node* cur = _head;
while (cur)
{
if(cur->_col == BLACK)
beach++;
cur = cur->_left;
}
bool rbdistance = RBDistance(_head,beach,0);
bool order = rbOrder();
return rr && rbdistance && order;
}
private:
bool isRRTree(Node* head)
{
if (head == nullptr)
return true;
if (head->_col == RED)
{
if (head->_left && head->_left->_col == RED)
{
cout << "红色与红色相连接" << endl;
return false;
}
if (head->_right && head->_right->_col == RED)
{
cout << "红色与红色相连接" << endl;
return false;
}
}
return isRRTree(head->_left) && isRRTree(head->_right);
}
bool RBDistance(Node * head, int beach, int count)
{
if (head == nullptr)
{
if (count != beach)
{
cout << "每条路径的黑色节点不相同" << endl;
return false;
}
return true;
}
return RBDistance(head->_left, beach, head->_col == BLACK ? count + 1 : count)
&& RBDistance(head->_right, beach, head->_col == BLACK ? count + 1 : count);
}
bool rbOrder()
{
stack<Node*> st;
Node* cur = _head;
while (cur)
{
st.push(cur);
cur = cur->_left;
}
Node* pre = nullptr;
while (!st.empty())
{
Node* top = st.top();
st.pop();
if (pre && pre->_kv.first > top->_kv.first)
{
cout << "不是有序的" << endl;
return false;
}
top = top->_right;
while (top)
{
st.push(top);
top = top->_left;
}
}
return true;
}
迭代器
在讲述迭代器的时候,首先得说明,红黑树的结构并不是像上面的图所示,而是拥有一个哨兵位头结点的。
以下例子对于两个节点的称呼:header即为哨兵位头节点,8即为根节点
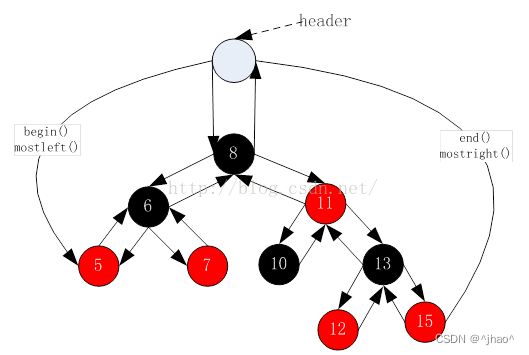
细节说明:
- 头节点的左指针指向的是最左节点(也就是最小节点 - - leftMost)
- 头节点的右指针指向最右节点(也就是最大节点 - - rightMost)
- 头节点的父亲节点指向的是根节点
为什么需要添加一个头节点方便进行迭代器设计呢?
个人认为最重要的原因在于节点遍历的时候倘若没有头节点,那么在operator++,operator–的两个逻辑当中不能采用同一套设计来实现,当没有头节点,我们只能将leftMost设置begin,而end只能放在根节点的父亲,也就是NULL,正序遍历的时候正好可以全部遍历完;但是当出现了从end()遍历到begin()位置,这样的设计就不能满足要求了。
上面这么说,那么加入迭代器肯定就能解决了!当倒叙遍历时,header只需要特判一下自己是不是头节点,如果是就跳转到rightMost,此时遍历到begin()也就简单了。
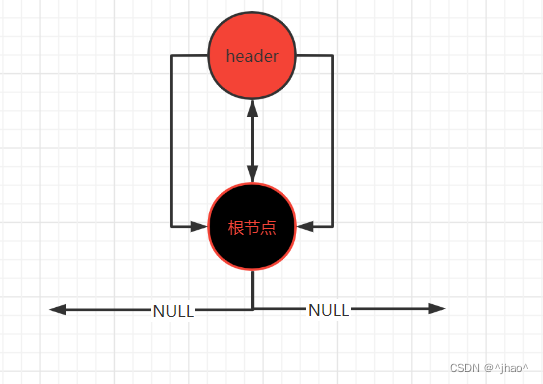
begin() 指向的是leftMost,end()指向的是头节点。
并且有一处设计的比较巧妙,就是将头节点的颜色设置成红色,由于头节点和根节点都能够通过 xx->_parent->_parent找到自己,并且根节点必须为黑色,所以我们要将两个节点进行区分,就选择将头节点的颜色设置成红色。
注意:添加头节点导致插入的判断条件发生变化
- 添加了哨兵位插入的逻辑需要稍微变化
while (parent->_col == RED && parent != _head )//parent->parent,因为此时有可能出现插入可能出现uncle为红色的情况,此时parent会走到头节点。 - 并且Insert函数需要每次插入更新leftMost以及rightMost。
顺序遍历和逆序遍历都以该图为基础
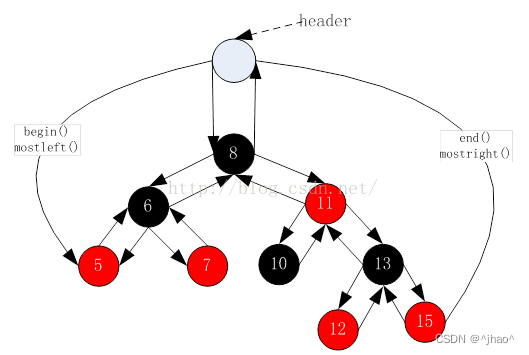
顺序遍历 Increament
顺序遍历的时候实际上走的是一个中序遍历,即左根右形式,那么当我们在当前节点,有如下几种情况。
- 1.右节点存在,如11这个节点,此时我们应当访问右节点的最左节点。
- 2.当右节点不存在,我们首先都需要向上面遍历,并找到
当前访问节点是父亲节点的左孩子的情况。 - 2.1 但是此时有特殊情况,当根节点没有右孩子的时候,若节点已经遍历到根位置,但同时就是rightMost,若外面使用迭代器遍历就会陷入死循环。
- 2.2 若有右孩子,就不会有上述问题。此时_node(迭代器封装的指针)到达了头节点的位置,正常遍历完,而pre在根节点的位置,此时恰好也不满足_node->_right == pre的条件,所以while循环结束,且_node也到达了end()的位置,遍历结束。
void Increament()
{
//右节点存在
if (_node->_right)
{
_node = _node->_right;
while (_node->_left)
{
_node = _node->_left;
}
}
else
{
//右节点不存在
Node* pre = _node;
_node = _node->_parent;
while (_node->_right == pre)
{
pre = _node;
_node = _node->_parent;
}
//特殊情况分析,与内核实现不同,我是定义前指针,源代码是父指针,这种情况当头节点没有右孩子的时候,头节点会在同一个位置死循环
//所以加上后面的条件解决这种情况。
if (pre->_right == _node)
{
//根节点没有右孩子
_node = pre;
}
}
}
逆序遍历 DeIncreament
逆序遍历正好与中序遍历相反,即右根左的顺序。
遍历情况:
1.若左节点存在,如8位置,则访问左节点的最右节点;
2.若左节点不存在,如12位置,就访问头节点的位置是当前节点位置的右孩子的位置,即11位置。
特殊情况:
我们一开始从end()位置出发,此时我们想要遍历的第一个元素是rightMost元素,而根据上面的遍历情况我们会走到leftMost位置,,所以这个时候我们可以判断是否当前位置为头节点,_node->_parent->_parent == _node && _node->_col == RED,此时上面所说的头节点的颜色为红色的情况也就用上了。
void DeIncreament()
{
//通过虚拟头节点的颜色辨别是头节点还是虚拟节点,太优雅了。
if (_node->_parent->_parent == _node && _node->_col == RED)
{
_node = _node->_right;
return;
}
if (_node->_left)
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else
{
Node* pre = _node;
_node = _node->_parent;
while (_node->_left == pre)
{
pre = _node;
_node = _node->_parent;
}
}
}
迭代器代码一览
template<class T>
class RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> Self;
private:
Node* _node;
public:
RBTreeIterator(Node* node)
:_node(node)
{
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
bool operator==(const Self& it)
{
return _node == it._node;
}
T* operator->()
{
return &(_node->_data);
}
Self& operator++()
{
Increament();
return *this;
}
Self& operator--()
{
DeIncreament();
return *this;
}
void Increament()
{
if (_node->_right)
{
_node = _node->_right;
while (_node->_left)
{
_node = _node->_left;
}
}
else
{
Node* pre = _node;
_node = _node->_parent;
while (_node->_right == pre)
{
pre = _node;
_node = _node->_parent;
}
//特殊情况分析,与内核实现不同,我是定义前指针,源代码是父指针,这种情况当头节点没有右孩子的时候,头节点会在同一个位置死循环
//所以加上后面的条件解决这种情况。
if (pre->_right == _node)
{
_node = pre;
}
}
}
void DeIncreament()
{
//通过虚拟头节点的颜色辨别是头节点还是虚拟节点,太优雅了。
if (_node->_parent->_parent == _node && _node->_col == RED)
{
_node = _node->_right;
return;
}
if (_node->_left)
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else
{
Node* pre = _node;
_node = _node->_parent;
while (_node->_left == pre)
{
pre = _node;
_node = _node->_parent;
}
}
}
T& operator*()
{
return _node->_data;
}
};
制造map/set
- 封装map,首先得更改Insert的返回值为pair<iterator,bool>,其中iterator就是该插入节点/已存在节点封装的迭代器,而bool值用来判断是否插入成功。
- 由于在Insert函数内部需要获取节点值当中的key值,但是在RBTree当中,他并不知道他被封装的是map还是set,所以此时需要在map/set当中传入第三个模板参数KOft,表示从节点获取Key值的方法。同时,这也决定了第一个参数传K,第二个参数传T。因为K可以在FInd函数当中使用,而T才是节点的值真正的类型。
所以set封装时,节点的值为const K,而map封装的时候节点的值时pair<const K,V> RBTree<K, pair<const K,V>, KOft> _map;,typedef typename RBTree<K, pair<const K, V>, KOft>::iterator iterator;由于节点是通过第二个参数传递,所以我们在map或set都可以将K设置为const,避免RBtree当中对K进行修改。- map想要实现operator[],此时只需要
return (insert(make_pair(key,V())).first)->second;直接调用插入是因为插入函数当存在时会返回红黑树节点的迭代器,不存在正好可以插入。
注意点:
- 由于红黑树当中的节点的值被设置成了const K,而pair赋值又是一个值一个值的赋值,但是在构造函数内部赋值此时无法对const 类型做修改,所以得在初始化列表初始化。

typedef RBTreeIterator<K, V> iterator;,typedef typename RBTree<K, pair<const K, V>,map中设置迭代器的两种方式,由于RBTree<K, pair<const K, V>是在运行时才会进行实体化,所以需要加入typename说明定义的是类型,让编译器暂时不做检查。
RBTree2.hpp
#pragma once
#include<iostream>
#include<stack>
using std::stack;
using std::cout;
using std::endl;
#include<windows.h>
enum Color
{
RED,
BLACK
};
//T就是节点的值 pair<srting,int> string 之类的
template<class T>
class RBTreeNode
{
public:
//const std::pair<const K, V>& data
RBTreeNode(const T& data)
:_col(RED)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(data)
{
//若加上了这个const K ,由于pair赋值 的时候是一个个赋值,由于const K不能被赋值,所以必须放在初始化列表处初始化,否则会报错
//_data = data;
}
Color _col;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;//std::pair<const K, V>
};
template<class T>
class RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T> Self;
private:
Node* _node;
public:
RBTreeIterator(Node* node)
:_node(node)
{
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
bool operator==(const Self& it)
{
return _node == it._node;
}
T* operator->()
{
return &(_node->_data);
}
Self& operator++()
{
Increament();
return *this;
}
Self& operator--()
{
DeIncreament();
return *this;
}
void Increament()
{
if (_node->_right)
{
_node = _node->_right;
while (_node->_left)
{
_node = _node->_left;
}
}
else
{
Node* pre = _node;
_node = _node->_parent;
while (_node->_right == pre)
{
pre = _node;
_node = _node->_parent;
}
//特殊情况分析,与内核实现不同,我是定义前指针,源代码是父指针,这种情况当头节点没有右孩子的时候,头节点会在同一个位置死循环
//所以加上后面的条件解决这种情况。
if (pre->_right == _node)
{
_node = pre;
}
}
}
void DeIncreament()
{
//通过虚拟头节点的颜色辨别是头节点还是虚拟节点,太优雅了。
if (_node->_parent->_parent == _node && _node->_col == RED)
{
_node = _node->_right;
return;
}
if (_node->_left)
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else
{
Node* pre = _node;
_node = _node->_parent;
while (_node->_left == pre)
{
pre = _node;
_node = _node->_parent;
}
}
}
T& operator*()
{
return _node->_data;
}
};
template<class K,class T,class KOfT>
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef RBTreeIterator<T> iterator;
private:
Node* _head;
private:
bool isRRTree(Node* head)
{
if (head == nullptr)
return true;
if (head->_col == RED)
{
if (head->_left && head->_left->_col == RED)
{
cout << "红色与红色相连接" << endl;
return false;
}
if (head->_right && head->_right->_col == RED)
{
cout << "红色与红色相连接" << endl;
return false;
}
}
return isRRTree(head->_left) && isRRTree(head->_right);
}
bool RBDistance(Node * head, int beach, int count)
{
if (head == nullptr)
{
if (count != beach)
{
cout << "每条路径的黑色节点不相同" << endl;
return false;
}
return true;
}
return RBDistance(head->_left, beach, head->_col == BLACK ? count + 1 : count)
&& RBDistance(head->_right, beach, head->_col == BLACK ? count + 1 : count);
}
bool rbOrder()
{
stack<Node*> st;
Node* cur = GetHead();
while (cur)
{
st.push(cur);
cur = cur->_left;
}
Node* pre = nullptr;
while (!st.empty())
{
Node* top = st.top();
st.pop();
if (pre && pre->_data.first > top->_data.first)
{
cout << "不是有序的" << endl;
return false;
}
top = top->_right;
while (top)
{
st.push(top);
top = top->_left;
}
}
return true;
}
public:
//构造函数,制造哨兵位的头节点
RBTree()
{
_head = new Node(T());
_head->_left = _head;
_head->_right = _head;
_head->_parent = nullptr;//通过_parent可以得知真正的头
}
Node* GetHead()
{
return _head->_parent;
}
iterator begin()
{
//开始是最左节点
Node* cur = GetHead();
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
//结尾是哨兵位的头节点
return iterator(_head);
}
//没有添加哨兵位头节点的做法
//iterator begin2()
//{
// Node* cur = _head;
// while (cur->_right)
// {
// cur = cur->_right;
// }
//
// return iterator(cur);
//}
//iterator end2()
//{
// //Node* cur = _head;
// //while (cur->_right)
// //{
// // cur = cur->_right;
// //}
// //return iterator(cur);
// return iterator(nullptr);
//}
//void RotateR(Node* parent)
//{
// Node* left = parent->_left;
// Node* lRight = left->_right;
// Node* pParent = parent->_parent;
// if (lRight)
// {
// lRight->_parent = parent;
// }
// parent->_left = left->_right;
// left->_right = parent;
// parent->_parent = left;
// if(lRight)
// lRight->_parent = parent;
// left->_parent = pParent;//指向父节点
// if (pParent)
// {
// if (pParent->_data.first > left->_data.first)
// {
// pParent->_left = left;
// }
// else
// {
// pParent->_right = left;
// }
// }
// else
// {
// _head->_parent = left;
// }
//}
void RotateR(Node* parent)
{
Node* left = parent->_left;
Node* lRight = left->_right;
Node* pParent = parent->_parent;
bool isRight = pParent->_right == parent ? true : false;
parent->_left = lRight;
parent->_parent = left;
left->_parent = pParent;
if (lRight)
{
lRight->_parent = parent;
}
left->_right = parent;
//由于根的变化,所以这里的逻辑需要改变
if (pParent == _head)
{
pParent->_parent = left;
return;
}
if (isRight)
{
pParent->_right = left;
}
else
{
pParent->_left = left;
}
}
void RotateL(Node* parent)
{
Node* right = parent->_right;
Node* rLeft = right->_left;
Node* pParent = parent->_parent;
bool isRight = pParent->_right == parent ? true : false;
parent->_right = rLeft;
if (rLeft)
{
rLeft->_parent = parent;
}
parent->_parent = right;
right->_left = parent;
right->_parent = pParent;
//如果是哨兵位的头节点,此时左右不能用于连接
if (pParent == _head)
{
pParent->_parent = right;
return;
}
if (isRight)
{
pParent->_right = right;
}
else
{
pParent->_left = right;
}
}
Node* LeftMost()
{
Node* cur = GetHead();
while (cur && cur->_left)
{
cur = cur->_left;
}
return cur;
}
Node* RightMost()
{
Node* cur = GetHead();
while (cur && cur->_right)
{
cur = cur->_right;
}
return cur;
}
bool IsRBTree()
{
bool rr = isRRTree(GetHead());
int beach = 0;
Node* cur = GetHead();
while (cur)
{
if(cur->_col == BLACK)
beach++;
cur = cur->_left;
}
bool rbdistance = RBDistance(GetHead(),beach,0);
bool order = rbOrder();
return rr && rbdistance && order;
}
iterator find(const K& key)
{
Node* cur = _head->_parent;
if (cur == nullptr)
return iterator(_head);
KOfT koft;
while (cur)
{
if (koft(cur->_data) > key)
{
cur = cur->_left;
}
else if (koft(cur->_data) < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return iterator(_head);
}
pair<iterator,bool> Insert(const T& data)
{
KOfT koft;
// 由于这个地方没法判断T的类型,所以要取key值需要仿函数的帮助
const K& key = koft(data);
Node* newNode = new Node(data);
Node* trueHead = _head->_parent;
if (trueHead == nullptr)
{
//头节点和虚拟节点的相互指向
//newNode 就是下一次的trueHead,这个地方需要更新虚拟节点的左右节点
_head->_parent = newNode;
newNode->_parent = _head;
_head->_left = newNode;
_head->_right = newNode;
newNode->_col = BLACK;
return pair<iterator,bool>(iterator(newNode),true);
}
//printf("%p\n", _head);
Node* cur = trueHead;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (koft(cur->_data) > key)
{
cur = cur->_left;
}
else if (koft(cur->_data) < key)
{
cur = cur->_right;
}
else
{
delete newNode;
//已经存在的话直接返回即可
return pair<iterator,bool>(iterator(cur),false);//键值冗余
}
}
if (koft(parent->_data) > key)
{
parent->_left = newNode;
newNode->_parent = parent;
}
else
{
parent->_right = newNode;
newNode->_parent = parent;
}
//此时需要调整节点的颜色
//parent此时是父亲节点
while (parent->_col == RED && parent != _head )//parent->parent is bug,because i modify the struct.
{
if (parent->_col == BLACK)
{
break;
}
else if (parent->_col == RED)
{
Node* g = parent->_parent;
Node* uncle = g->_left == parent ? g->_right : g->_left;
if (uncle && uncle->_col == RED)
{
//情况一:优先判断,这种情况处理方式更简单
uncle->_col = parent->_col = BLACK;
g->_col = RED;
//向上迭代,此时g相当于新插入节点
parent = g->_parent;
newNode = g;//这个很重要
continue;
}
else
{
//第二种情况,需要翻转
//要么uncle不存在,要么uncle为黑
//需要判断是否是左右或者右左结构
if (g->_left == parent)
{
if (parent->_left == newNode)
{
//右单旋
RotateR(g);
parent->_col = BLACK;
g->_col = RED;
}
else
{
//左右双旋
RotateL(parent);
RotateR(g);
newNode->_col = BLACK;
g->_col = RED;
}
}
else
{
if (parent->_right == newNode)
{
//左单旋
RotateL(g);
g->_col = RED;
parent->_col = BLACK;
}
else
{
//右左双旋
RotateR(parent);
RotateL(g);
newNode->_col = BLACK;
g->_col = RED;
}
}
break;
}
}
}
//这里的头会发生变化吗?
trueHead = GetHead();
trueHead->_col = BLACK;//旋转过后的结果需要将头部置成黑色。
Node* leftMost = LeftMost();
//cout << "leftMost" << leftMost << leftMost->_data.first << endl;
//虚拟头节点的左右需要重新指向
_head->_left = leftMost;//方便++ --
Node* rightMost = RightMost();
//cout << "rightMost" << rightMost << endl;
_head->_right = rightMost;//方便++ --
//Sleep(1000);
return pair<iterator,bool>(iterator(newNode),true);
}
};
map.hpp
#pragma once
#include<iostream>
#include"RBTree2.h"
namespace ljh
{
template<class K,class V>
class map
{
struct KOft
{
const K& operator()(const pair<const K,V>& kv)
{
return kv.first;
}
};
private:
RBTree<K, pair<const K,V>, KOft> _map;
public:
//typedef RBTreeIterator<K, V> iterator;
//两种方式,但是下面这种由于模板没有实例化所以需要加typename
typedef typename RBTree<K, pair<const K, V>, KOft>::iterator iterator;
public:
iterator begin()
{
return _map.begin();
}
iterator end()
{
return _map.end();
}
V& operator[](const K& key)
{
//找不到就插入
//方法1:
//iterator result = _map.find(key);
//if(result == end())
//{
// std::pair<iterator, bool> it = insert(std::make_pair( key,V()) );
// return it.first->second;
//}
//return result;
//方法2:
return (insert(make_pair(key,V())).first)->second;
}
pair<iterator,bool> insert(const pair<const K,V>& kv)
{
return _map.Insert(kv);
}
};
void test_map()
{
map<string, string> dict;
dict.insert(make_pair("sort", ""));
dict.insert(make_pair("string", ""));
dict.insert(make_pair("debug","a"));
dict.insert(make_pair("set", ""));
dict["make"];
dict["debug"] = "x";
dict["insert"] = "";
map<string, string>::iterator it = dict.begin();
while (it != dict.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
cout << endl;
}
}
//严重性 代码 说明 项目 文件 行 禁止显示状态
//错误 C2280 “std::pair<const K, V>& std::pair<const K, V>::operator =(volatile const std::pair<const K, V>&)”: 尝试引用已删除的函数 RBTree C : \Users\asus\source\repos\RBTree\RBTree\RBTree2.h 24
set.hpp
#pragma once
#include<iostream>
#include"map.h"
namespace ljh
{
template<class K>
class set
{
struct KOft
{
const K& operator()(const K& k)
{
return k;
}
};
private:
RBTree<K, const K, KOft> _set;
public:
typedef typename RBTree<K, const K, KOft>::iterator iterator;
public:
iterator begin()
{
return _set.begin();
}
iterator end()
{
return _set.end();
}
pair<iterator,bool> insert(const K& key)
{
return _set.Insert(key);
}
};
}
总结
gitee链接:https://gitee.com/wuyi-ljh/test-43—testing/tree/master/RBTree3