本文介绍一些常用的优化方法、处理过拟合的一些手段、批归一化的方法和超参数的选取。

一、优化器

回忆：随机梯度下降(SGD)及动量(momentum)

训练中需要调整学习率 $\eta$

随机梯度下降算法对每批数据 $(x^{(i)},t^{(i)})$ 进行优化，其中J 为损失函数：

$g = \triangledown _{\theta }J(\theta ;x^{(i)},t^{(i)})$

$\theta = \theta - \eta g$

基于动量的更新过程：

$v = \gamma v-\eta g$

$\theta =\theta +v$

我们前面学习地更新 $\eta$ 的方法，都是对所有的变量进行调整的，是全局且同等地调整各个参数的学习率，这并不一定是最优的学习方式(如不同层的权值的更新率不一定非要相同)，

那么我们能不能让它自适应地对不同参数进行不同学习率地调整呢？

1.1 Adagrad算法

一种典型的自适应学习率算法

梯度记为 $g = \triangledown _{\theta }J(\theta ;x^{(i)},t^{(i)})$

更新过程：

$c = c+g^{2}$

$\theta =\theta -\eta \frac{g}{\sqrt{c+\epsilon }}$

$\epsilon$ 通常在 $10^{-4}$ 和 $10^{-8}$ 之间

引入了变量c，来积累历史的梯度的平方。
更新的时候由原来的 $\theta = \theta - \eta g$ 变为了 $\theta =\theta -\eta \frac{g}{\sqrt{c+\epsilon }}$

注：如上 $g^{2}$ 表示g这个向量每个元素的平方，依旧是向量；同理下方开根号操作也是，都是逐元素操作。

例子：

假设某次迭代中， $c_{3}=90,\: c_{9}=2,$ 那么

$\Delta \theta _{3}=- \frac{\eta}{\sqrt{90+\epsilon }}g_{3}$

$\Delta \theta _{9}=- \frac{\eta}{\sqrt{2+\epsilon }}g_{9}$

显然 $\theta _{9}$ 的有效学习率 $\frac{\eta}{\sqrt{2+\epsilon }}$ 比 $\theta _{3}$ 的有效学习率 $\frac{\eta}{\sqrt{90+\epsilon }}$ 大，这说明虽然在前面的历史过程中，第九个参数的梯度的绝对值比较小，但在本次就多更新一些；相反的第三次参数的梯度的绝对值比较大，在更新时就少更新一些。这样就达成了实际学习率的一些平衡，避免了梯度小更新就小的问题。

引入 c 对不同参数的更新过程进行归一化(平衡)

本方法有什么缺点吗？

由于 $c = c+g^{2}$ 这会使c递增，导致有效学习率 $\frac{\eta}{\sqrt{c+\epsilon }}$ 一直变小。这可能会导致早停(early stopping)。过早停止了优化。

那我们怎么解决这个问题呢？

1.2 RMSprop算法

RMSProp算法在Adagrad的基础上提出改进，以解决学习率单调下降的问题；

引入一个遗忘因子 $\gamma$

$c= \gamma c+(1-\gamma )g^{2}$

$\theta =\theta -\eta \frac{g}{\sqrt{c+\epsilon }}$

$\gamma$ 通常为 0.9，0.99，0.999

RMSProp依然根据梯度的大小来调整学习率，但不同于Adagrad，学习率不会一直单调下降。

Adagrad vs RMSProp

adagrad算法

$Adagrad: \, c(t)=c(t-1)+g(t)^{2}=c(0)+g(1)^{2}+g(2)^{2}+...+g(t)^{2}$

$g(1)^{2},g(2)^{2},...,g(t)^{2}$ 平等贡献于c(t)

RMSProp算法

$RMSProp:\, c(t)=\gamma c(t-1)+(1+\gamma )g(t)^{2}=\gamma^{t}c(0)+\gamma^{t-1}(1-\gamma )g(1)^{2}+\gamma^{t-2}(1-\gamma )g(2)^{2}+...+\gamma(1-\gamma )g(t-1)^{2}+(1-\gamma )g(t)^{2}$

对于k<<t ， $g(k)^{2}$ 对c(t)的贡献指数级衰减，即比较看重近期的g的平方，这样c可能增加也可能减少。

缺点：如何引入动量？

1.3 Adam算法

由 kingma and Ba (2015)提出。默认算法。

简单形式

$m=\beta _{1}m+(1-\beta _{1})g$

$c=\beta _{2}c+(1-\beta _{2})g^{2}$

$\theta =\theta -\eta \frac{m}{\sqrt{c+\epsilon }}$

完整形式(“warm up”)

$m=\beta _{1}m+(1-\beta _{1})g,\:\: \: \: \: \: m_{t}=\frac{m}{1-\beta _{1}^{t}}$

$c=\beta _{2}c+(1-\beta _{2})g^{2},\:\: \: \: \: \: \: c_{t}=\frac{m}{1-\beta _{2}^{t}}$

$\theta =\theta -\eta \frac{m}{\sqrt{c+\epsilon }}$

其中 m 表示积攒历史梯度，c 表示积攒历史平方梯度，t 表示迭代次数。

建议值： $\epsilon =10^{-8}$ $\beta_{1}=0.9\: \:\: \: \beta_{2}=0.99$

1.4 优化器小结

关于优化器的更多细节：CS231n Convolutional Neural Networks for Visual Recognition

二、处理过拟合

回忆：多项式回归问题

2.1 过拟合

什么是过拟合？

对训练集拟合得很好，但在验证集表现较差。

神经网络通常含有大量参数 (数百万甚至数十亿)，容易过拟合；

参数正则化是一种处理策略

其它技巧

早停(Early stopping)
随机失活(Dropout)
数据增强(data augmentation)

2.1.1 早停

当发现训练损失逐渐下降，但验证集损失逐渐上升时，停止优化。

注意：跟Adagrad优化引起的“早停”是两回事。

2.1.2 随机失活

在训练迭代过程中，以 p (通常为0.5)的概率随即舍弃掉每个隐含层神经元(输出置零)。

这些被置零的输出将用于在反向传播中计算梯度。

优点：

一个隐含层神经元不能依赖于其它存在的神经元，因此可以防止神经元出现复杂的相互协同。
相当于在合理的时间内训练了大量不同的网络，并将其结果平均。

测试过程:

使用“平均网络”，包含所有隐含层神经元

需要调整神经元输出的权重，用来弥补训练中只有一部分被激活的现象。

p=0.5 时，将权重减半
p=0.1 时，在权重上乘 1-p ，即0.9。

这样得到的结果与在大量网络上做平均得到的结果类似。

MNIST上的结果：

标准多层感知机
不用dropout的最好结果是160个错误样本
Dropout可以显著降低错误率

本例中还用了其他技巧，比如每个神经元的输入权重有个L2 正则化约束。

补充：

在一些实现里，测试中，1-p 乘在激活函数的输出即 f(Wx+b) 上，而不是乘在权重W上。

$a_{test}=(1-p)f(Wx+b)$

在一些实现里，训练中激活函数的输出改成

$a_{train}=\frac{1}{1-p}f(Wx+b)$

而测试中就不用了

实践中，p在底层设得很小，如0.2，但在高层设得更大，如0.5。
在某些平台，随机失活率被定义成每个神经元被保留的概率。

2.1.3 数据增强

$\begin{Bmatrix} x^{(n)},t^{(n)} \end{Bmatrix}$ 表示原本的训练集

在输入数据中加入一些变换： $x^{(n)}\rightarrow \widehat{x}^{(n)}$ 保持标签 $t^{(n)}$ 不变
使用增强后的训练集 $\begin{Bmatrix} x^{(n)},t^{(n)} \end{Bmatrix}\cup \begin{Bmatrix} \widehat{x}^{(n)},t^{(n)} \end{Bmatrix}$ 来训练模型

不同数据类型(文本，图像，音频)有不同的变换。

常用的图像变换：

随机
- 翻转 flips
- 平移 translations
- 缩放 crops and scales
- 拉伸 stretching
- 剪切 shearing
- 擦除 Cutout or erasing
- 混合 mixup
- 色彩变换 color jittering
- ……
上述变换的组合

随机翻转

随即缩放和裁剪

测试中可以

将测试图像缩放到模型要求的输入大小
剪裁一个区域 (通常是中心区域) 并输入到模型
剪裁多个并输入到模型, 对输出作平均

随机擦除

2.2 处理过拟合方法小结

三、批归一化

3.1 Internal covariate shift (内部协变量偏移)

当使用SGD时, 不同迭代次数时输入到神经网络的数据不同，可能导致某些层输出的分布在不同迭代次数时不同。

某个或一群神经元针对一批数据的输出分布：

由于神经网络比较深，一些层的分布可能就不那么相似了。

我们把：训练中，深度神经网络中间节点分布的变化叫做：内部协变量偏移(ICS)。

3.1.1 通过归一化来减少ICS

对每个标量形式的特征单独进行归一化，使其均值为0，方差为1

对于d维激活 $x=(x_{1},...,x_{d})$ , 做如下归一化：

$\widehat{x}_{i}=\frac{x_{i}-E[x_{i}]}{\sqrt{Var[x_{i}]}}$

保持该层的表达能力

$y_{i}=\gamma _{i}\widehat{x}_{i}+\beta _{i}$

若 $\gamma_{i}=\sqrt{Var[x_{i}]}$ 且 $\beta _{i}=E[x_{i}]$ ，恢复到原来的激活值。

3.2 批归一化(Batch Normalization, BN)

构建一个新的层

$y^{(n)}=BN_{\gamma ,\beta }(x^{(n)})$

向前计算(下式都是逐元素操作)

$\mu _{B}=\frac{1}{m}\sum_{n=1}^{M}x^{(n)}$
$\sigma _{B}^{2}=\frac{1}{m}\sum_{n=1}^{M}(x^{(n)}-\mu _{B})^{2}$
$\widehat{x}^{(n)}=\frac{x^{(n)}-\mu _{B}}{\sqrt{\sigma ^{2}_{B}+\epsilon }}$
$y^{(n)}=\gamma \widehat{x}^{(n)}+\beta$

3.2.1 推理过程

如果想追踪训练准确率，可以使用滑动平均。

3.2.2 在网络中的位置

通常应用在非线性层之前(根据实践经验)

前一层通常是线性转换层(全连接层或卷积层)

$y^{(l)}=W^{(l)}y^{(l-1)}+b^{(l)}$

偏置项可以忽略，因为BN的便宜项有相同的效果，因此

$y^{(l)}=BN(W^{(l)}y^{(l-1)})$

3.2.3 卷积神经网络中的批归一化

BN通常应用在卷积层之后
要求同一特征图里的不同元素以同样的方式进行归一化
对一个minibatch：
- 假设批大小为M，特征图大小为P*Q，那么均值和方差要基于MPQ个元素计算得到
- 对每个特征图(而不是每个激活)学习一堆参数 $\gamma _{i}$ 和 $\beta _{i}$
推理过程进行类似修改

3.2.4 优点

BN允许使用更大的学习率
BN对整个模型进行了正则化
- 对于某个训练样本，模型不会给出确定性的输出
- 可能不再需要Dropout

3.3 批归一化小结

其它归一化技巧：

四、超参数(Hyperparameters)选取

超参数: 控制算法行为，且不会被算法本身所更新。

通常决定了模型的能力(capacity)

对于一个深度学习模型，超参数包括：

层数, 每层的神经元数目
正则化系数
学习率 – 参数衰减率(Weight decay rate)
动量项(Momentum rate)
……

对于给定的数据集和任务，需要选择合适的超参数。

4.1 如何选择深度学习模型的架构?

熟悉数据集
- 看/听/闻…
与之前见过的数据/任务比较
- 样本数目
- 图像大小, 视频长度, 输入复杂度…
最好从在类似数据集或任务上表现良好的模型开始

4.2 如何选择其它超参数?

一个实践指南：

第1步: 观察初始损失。
第2步: 在一组小样本上过拟合。
第3步: 找到使损失下降的学习率。
第4步: 粗粒度改变学习率，训练1-5轮。
第5步: 细粒度改变学习率，训练更长时间。
第6步: 观察损失曲线。

第1步:观察初始损失

确保损失的计算是正确的
将权重衰减设为零

第2步:在一组小样本上过拟合

在一组少量样本的训练集上训练，尝试达到100%训练准确率。
- 可以保证从数据集预处理到输出的整个流程是正确的。
- 可以找出一些调整学习率的提示。
如果训练损失没有下降。
- 不好的初始化, 学习率太小, 模型太小。
如果训练损失变成Inf或NaN。
- 不好的初始化, 学习率太大。

第3步: 找到使损失下降的学习率

在全部数据上训练模型，并找到使损失值能够快速下降的学习率。
- 当损失值下降较慢时，将学习率缩小10倍。
- 使用较小的参数衰减。

第4步: 粗粒度改变学习率, 训练1-5轮

在上一步的基础上，尝试一些比较接近的学习率和衰减率。
常用的参数衰减率: 1e-4, 1e-5, 0。

第5步: 细粒度改变学习率, 训练更长时间

使用上一步找到的最好的学习率，并训练更长时间 (10-20 轮)，期间不改变学习率。

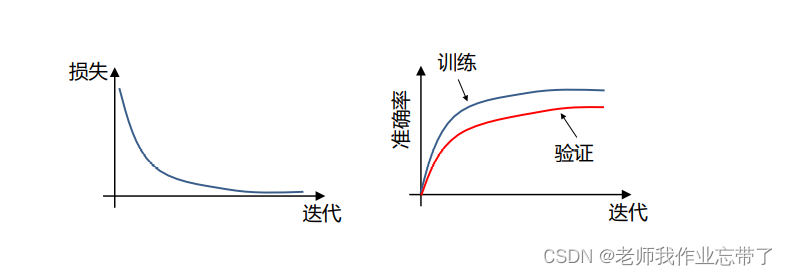
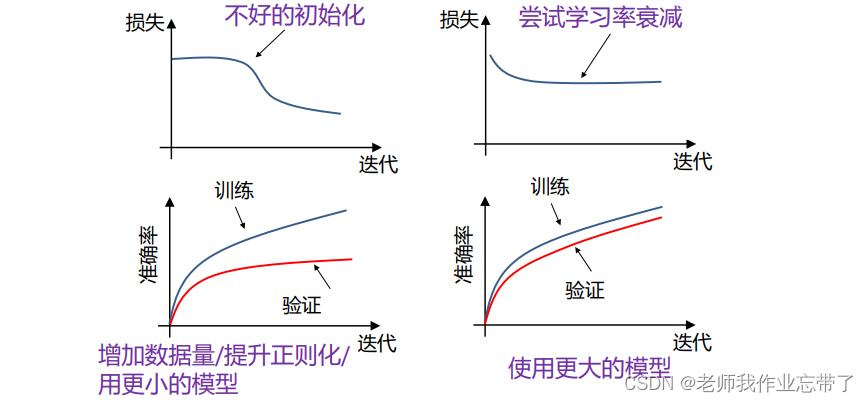
第6步: 观察损失曲线

训练损失通常用滑动平均绘制，否则会有很多点聚集在一起。

AL遮天传 DL-深度学习模型的训练技巧