我们之前学习的方法如决策树、回归分析、贝叶斯分析都可以看作是 三步走 的学习方法,即:
- 估计问题的特征(如分布)
- 做出模型假设(LSE、Decision、Tree、MAP、MLE )
- 找到最优的参数
那么有没有一种学习方法 不遵循模型假设+参数估计 呢?今天,基于实例的学习方法,它来了!
动机
人们通过记忆和行动来推理学习,思考即回忆、进行类比
- 近朱者赤近墨者黑

- 找到和这张图最相似的10张图片

- 找到两个基因组之间所有匹配的基因片段

那么机器也可以借鉴人类的这种方法,对于已有的记忆进行类比,看一看和记忆中的哪一部分最相像。
一些名词概念
参数化(Parametric) vs 非参数化(Non-parametric)
参数化:
- 设定一个特定的函数形式
- 优点:简单,容易估计和解释
- 缺点:可能存在很大的偏置:实际的数据分布可能不遵循假设的分布
非参数化:
- 分布或密度的估计是数据驱动的(data-driven)
- 需要事先对函数形式做的估计很少
基于实例的学习
无需构建模型--仅存储所有的训练样例
直到有新的样例需要分类才开始进行处理
概念表示:

简单来说就是我们给定一个范围,只要不超过这个范围,我们都认为A和B是一类。
一、最近邻(1-NN)
最近邻(1-NN)介绍 :
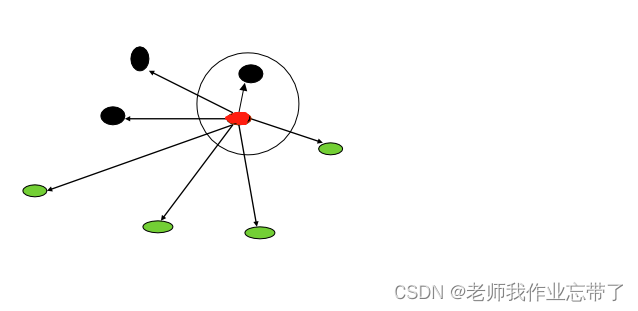
我们描述一个相似度,可以用他们之间的距离来表示,如下图很明显上方的这个点距离中间的这个点是最近的:
下面我们看一个简单的例子:
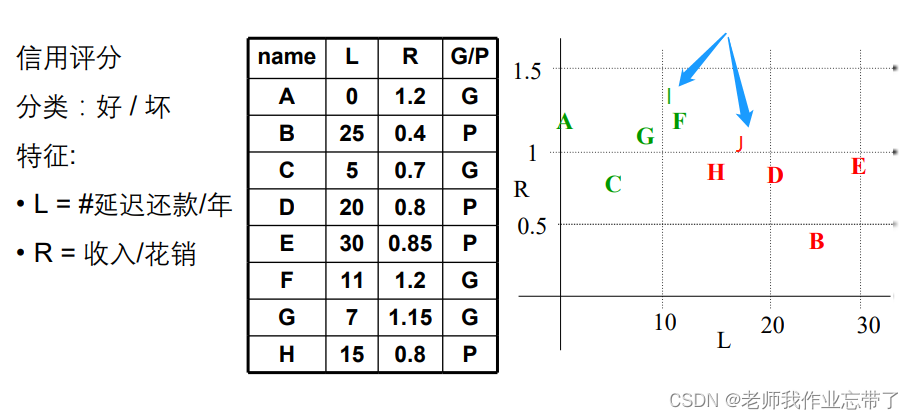
如图是一张用户是否具有可信度的表格,四列分别表示姓名、每年延迟还款的次数、收入与花销的比值以及该用户是否可信。
在右边可信的用户为绿色,不可信用户为红色,假如这时候来了新的用户,经计算用户I、J坐标如图,那么可见用户I离F最近,认为他们是一类的,可信;用户J离H最近,认为他们是一类的,不可信;
当然谁离谁近这是我们看出来的,正常情况下我们应该通过距离公式去计算,比如:

注:这里之所以缩放距离是因为横纵坐标数值差异比较明显,结果容易受到影响。当然这里对于1-NN只是比较个距离不放缩也可以,但对于后面K-NN就可以通过这种加权的方式淡化差异。
最近邻的解释:
对于任意欧氏空间的离散点集合S,以几乎所有的点x,S中一定有一个和x最接近的点。
光看这句话觉得是句废话,我也这样觉得。如下图,每个点都有自己的“管辖范围”,只要你落在这个点的“区域”内,那么你就是离它最近的,也是最相似的。
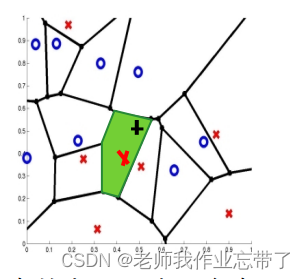
没有说所有的点是因为有些点可能在边界上,可能和两个或者多个点等距。
理论结果:
无限多训练样本下1-NN的错误率界限:
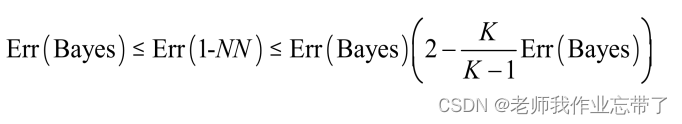
因此1-NN的错误率不大于Bayes方法错误率的2倍,可见还是可行的。
思考:
1 . 假如一个点(如下图K),即离F近又离H近怎么办?
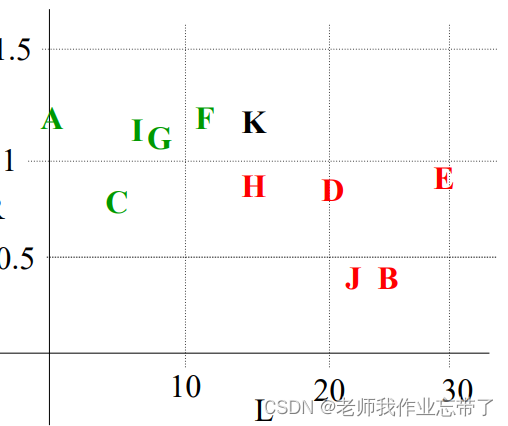
答:常用的三种办法 a.随机选择一个 b.以概率选择 c.再去看下一个离谁近
2 . 最近的便是噪声怎么办?
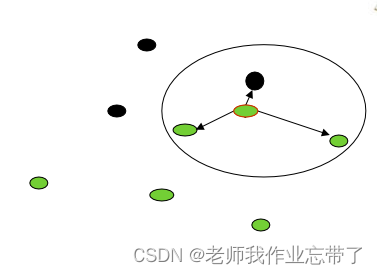
答:用不止一个邻居,在邻居中进行"投票" ---------------> k-近邻(KNN)
二、k-近邻(KNN)
k-近邻(KNN)介绍:
使用不止一个点的距离进行计算, 示例:
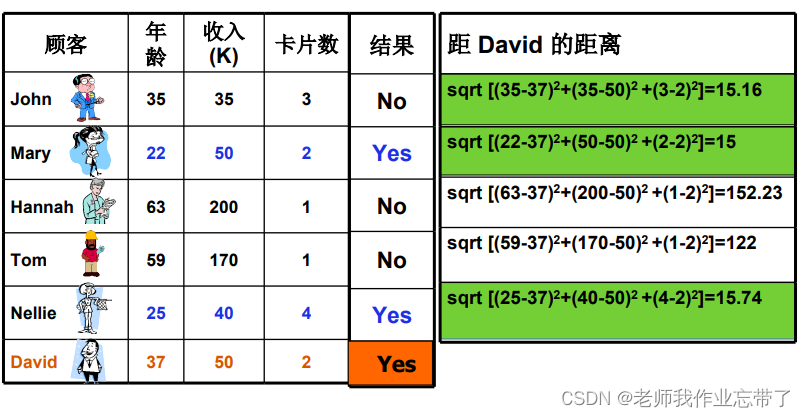
还是用户是否可信,这次有三个变量:年龄、收入、卡片数,我们可以看到右侧以新用户David为基准点有三组数是比较小的(绿色),说明这三者(John、Mary、Nellie)与David是一类的,经过投票:No、Yes、Yes---->Yes, 最后认为David是可新用户。
下面我们将会按以下顺序讨论KNN:
- 距离度量公式
- 属性的归一化与加权
- 连续取值目标函数
- 数字K的选择
- 打破平局(每个近邻都属于不同的类)
- 效率-->KD-Tree
1. 距离度量
选择合适的距离度量公式


2. 属性
邻居间的距离可能会被某些取值特别大的属性所支配
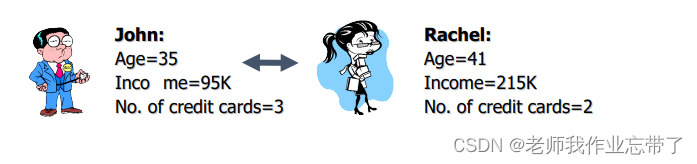
因此对特征进行归一化是非常重要的(把数值归一化到 [0-1])。
- Log, Max-Min, Sum...
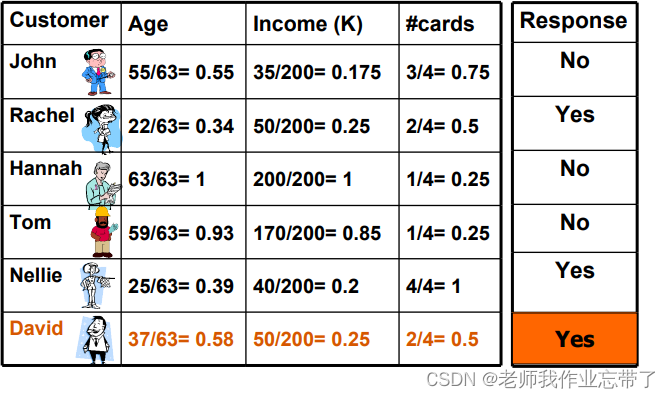
如图当进行归一化后,David的可信结果为Yes。
但仅是这样归一化后对于一些重要特征反而显得决定性作用不那么强了,因此需要进行属性加权:
在距离空间对维度进行缩放,wk=0——>消除对应的维度(特征)
一个可能的加权方法:
- 使用 互信息/(属性、类别)
H: 熵(entropy)
3. 连续取值目标函数
对于离散型输出,我们可以进行投票
对于连续型输出,可以观察k个近邻训练样例的均值
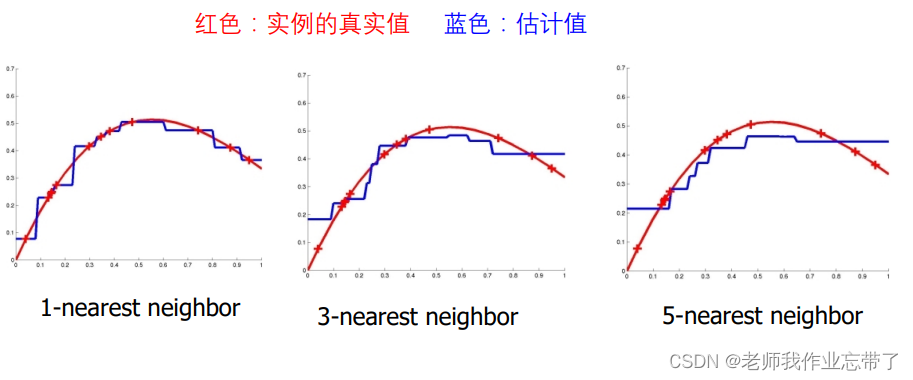
4. k的选择
- 多数情况下我们让k=3
- 取决于训练样例的数目,更大的k不一定带来更好的效果
- 交叉验证,每次拿一个样例作为测试,所有其他的作为训练样例
- KNN是稳定的,样例中小的混乱不会对结果有非常大的影响
5. 打破平局
如果K=3并且每个近邻都属于不同的类:
- P(w|X) = 1/3
- 找一个新的邻居(第四个)
- 取最近的邻居所属类
- 随机选一个
- ...
之后会讨论一个更好的解决办法
6. 关于效率
KNN算法把所有的计算放在新实例来到时,实时计算开销大。
为了加速对最近邻居的选择
- 先检验临近的点,忽略比目前找到最近的点更远的点
通过 KD-tree 来实现:
- KD-tree: k 维度的树(数据点的维度是 k)
- 基于树的数据结构
- 递归地将点划分到和坐标轴平行的方形区域内
KD-Tree构建:
比如空间中有一堆点:
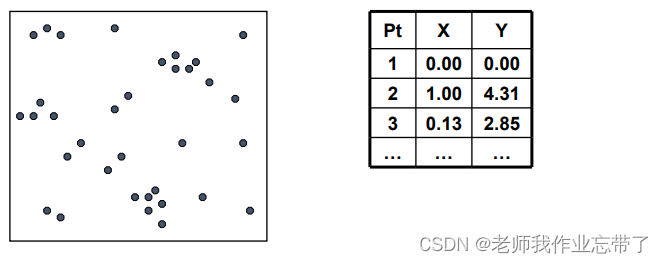
我们可以选择一个维度 X 和分界值 V 将数据点分为两组:X > V 和 X <= V:
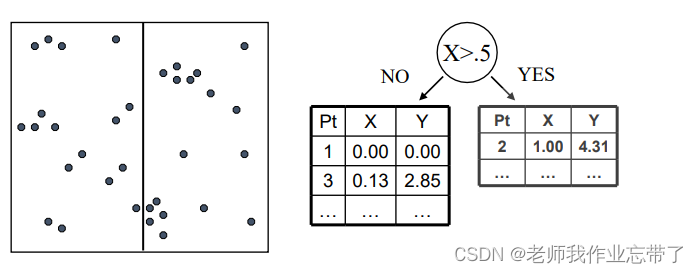
接下来分别考虑每个组,并再次分割(可以沿相同或不同的维度)
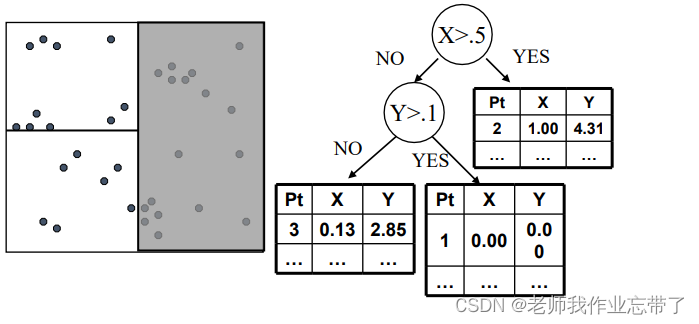
持续分割每个集合中的数据点,从而构建一个树形结构。每个叶节点表示为一系列数据点的列表。
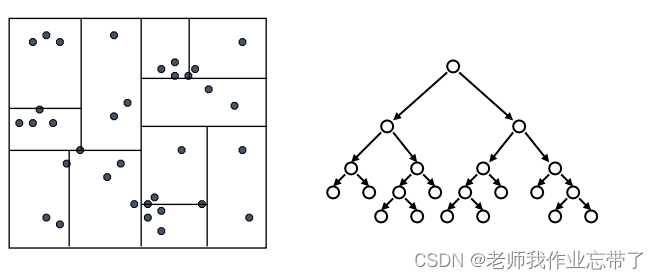
在每个叶节点维护一个额外信息:这个节点下所有数据点的 (紧) 边界。
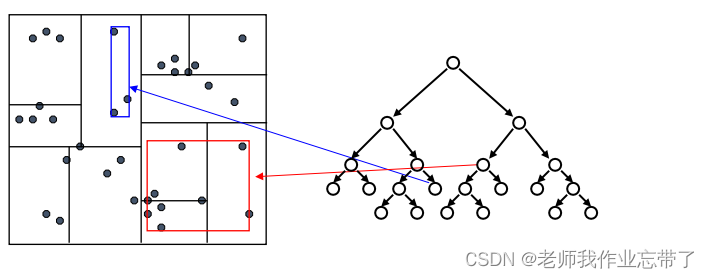
用启发式的方法去决定如何分割:
沿哪个维度分割?
- 范围最宽的维度
分割的值怎么取?
- 数据点在分割维度的中位数
什么时候停止分割?
- 当剩余的数据点少于 m,或者
- 区域的宽度达到最小值
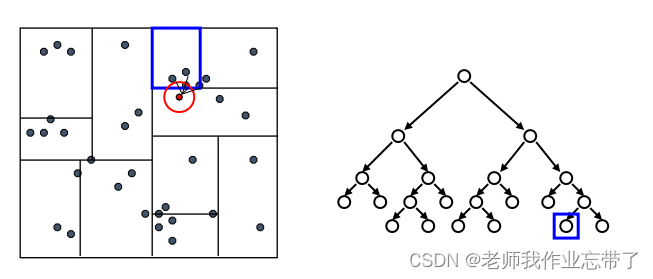
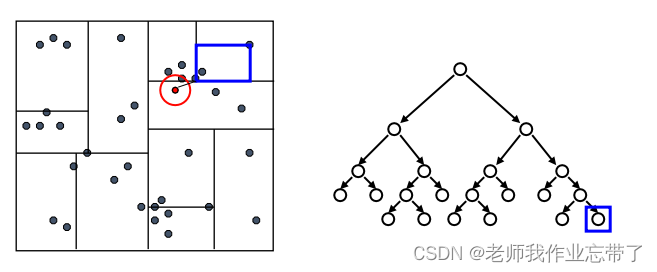
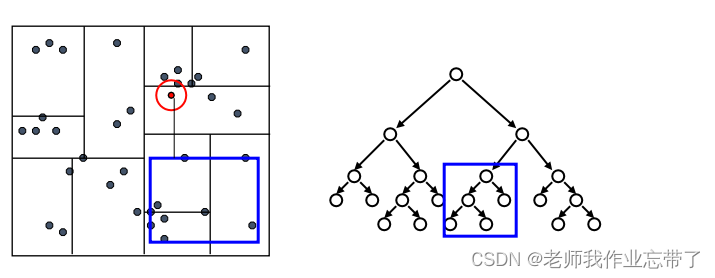
KD-Tree查询:
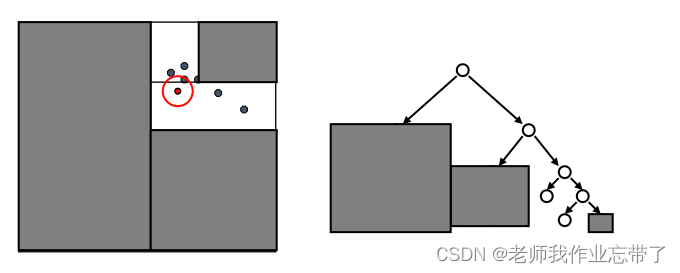
先检验临近的点:关注距离所查询数据点最近的树的分支
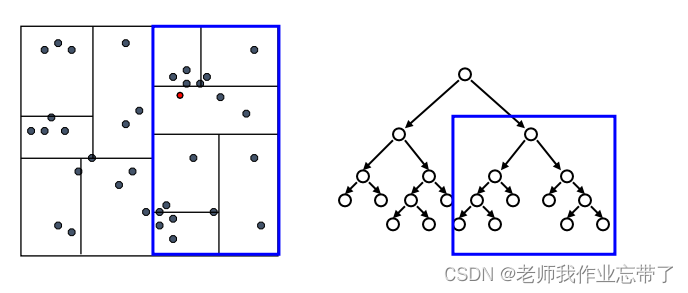
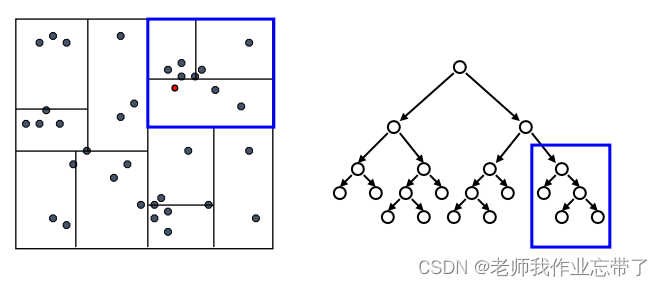
达到一个叶节点后:计算节点中每个数据点距离目标点的距离
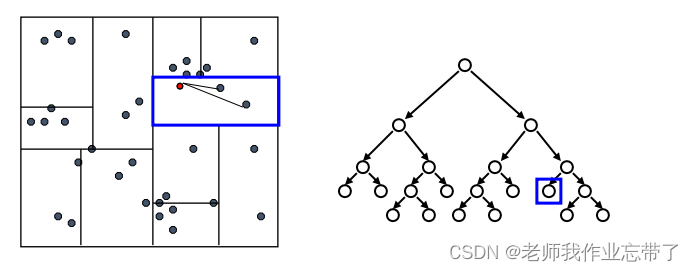
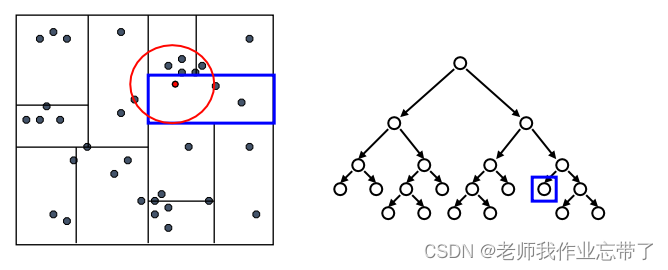
接着回溯检验我们访问过的每个树节点的另一个分支
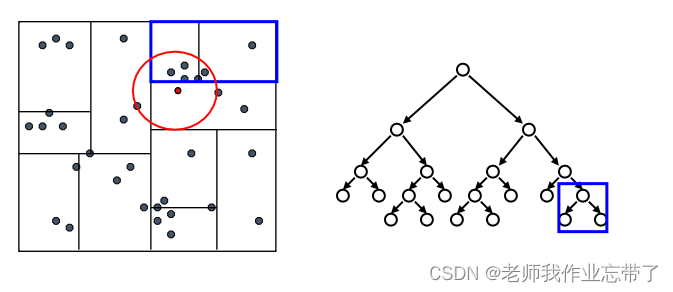
每次我们找到一个最近的点,就更新距离的上界
利用这个最近距离以及每个树节点下数据的边界信息, 我们可以对一部分不可能包含最近邻居的分支进行剪枝
KNN优点
• 概念上很简单,但可以处理复杂的问题(以及复杂的目标函数)
• e.g. 图片分类
• 通过对k-近邻的平均,对噪声数据更鲁棒
• 容易理解:预测结果可解释(最近邻居)
• 训练样例中呈现的信息不会丢失
• 因为样例本身被显式地存储下来了
• 实现简单、稳定、没有参数(除了 k)
• 方便进行 leave-one-out 测试
KNN缺点
• 内存开销
• 需要大量的空间存储所有样例
• 通常来说,需要存储任意两个点之间的距离 O(n 2 ) ; K-DTrees O(nlogn)
• CPU 开销
• 分类新样本需要更多的时间(因此多用在离线场景)
• 很难确定一个合适的距离函数
• 特别是当样本是由复杂的符号表示时
• 不相关的特征 对距离的度量有负面的影响
下一个问题
回忆:用多个邻居使得对噪声数据鲁棒 这些邻居的贡献是一样的吗?
办法:对数据进行加权,更接近所查询数据点的邻居赋予更大的权重。
注:上面是给属性加权,这里是根据数据离的远近进行数据加权。
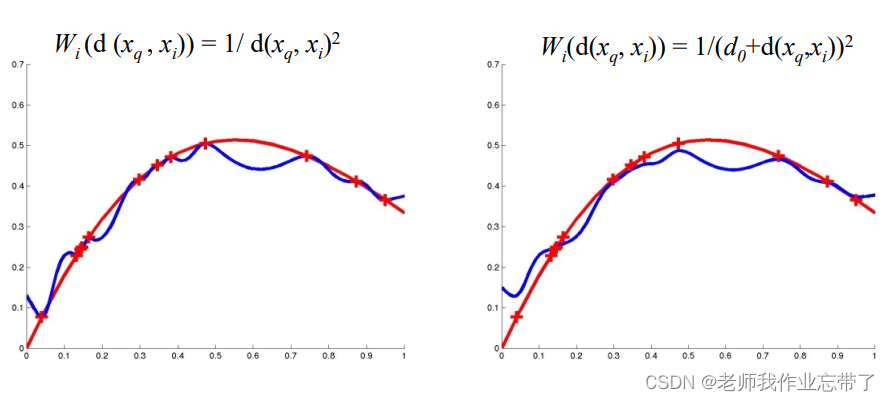
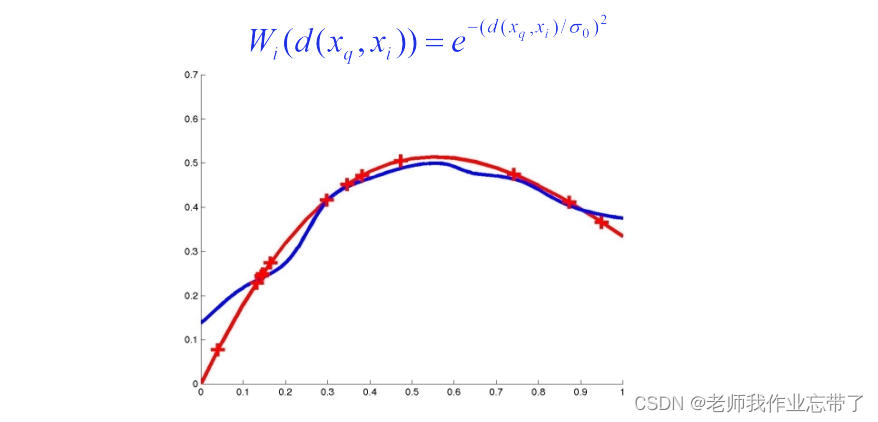
三、距离加权 KNN
一种加权函数
:查询数据点与 xi之间的关系
- K(·) :决定每个数据点权重的核函数
输出: 加权平均:
核函数 K(d(xi , xq ))
- 1/d 2 , e -d , 1/(1+d), … 应该和距离 d 成反比
回顾:
距离加权:
四、总览
1-NN
基于记忆的学习器:4 个要素
- 一种距离度量 欧式距离
- 使用多少个邻居? 一个
- 一个加权函数(加权) 无
- 如何使用已知的邻居节点? 和邻居节点相同
K-NN
基于记忆的学习器:4 个要素
- 一种距离度量 欧式距离
- 使用多少个邻居? K 个
- 一个加权函数(加权) 无
- 如何使用已知的邻居节点? K 个邻居节点投票
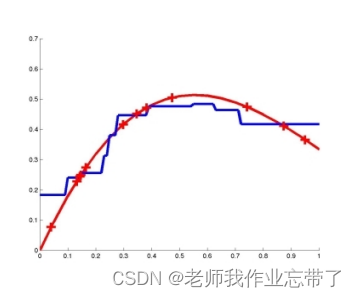
距离加权 KNN
基于记忆的学习器:4 个要素
- 一种距离度量 缩放的欧式距离
- 使用多少个邻居? 所有的,或K 个
- 一个加权函数(可选)
:核宽度。非常重要
- 如何使用已知的邻居节点? 每个输出的加权平均
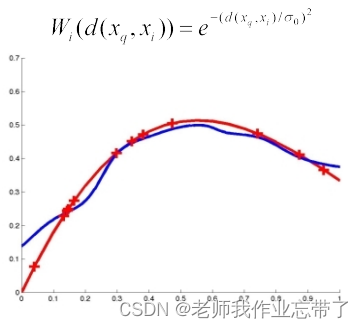
五、扩展: 局部加权回归
局部加权回归(Locally weighted regression)
- 回归:对实数值目标函数做估计/预测
- 局部:因为函数的估计是基于与所查询数据点相近的数据
- 加权:每个数据点的贡献由它们与所查询数据点的距离决定
局部加权回归(例子)
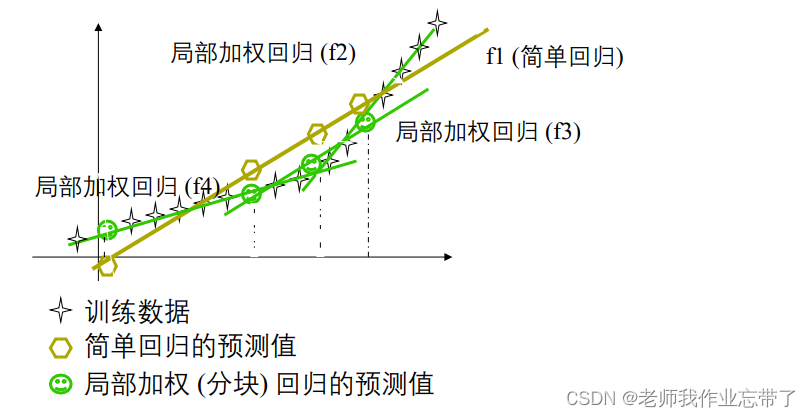
基于记忆的学习器:4 个要素
- 一种距离度量 缩放的欧式距离
- 使用多少个邻居? 所有的,或 K个
- 一个加权函数(可选)
:核宽度。非常重要
- 如何使用已知的邻居节点? 首先构建一个局部的线性模型。拟合 β 最小化局部的加权平方误差和:
那么
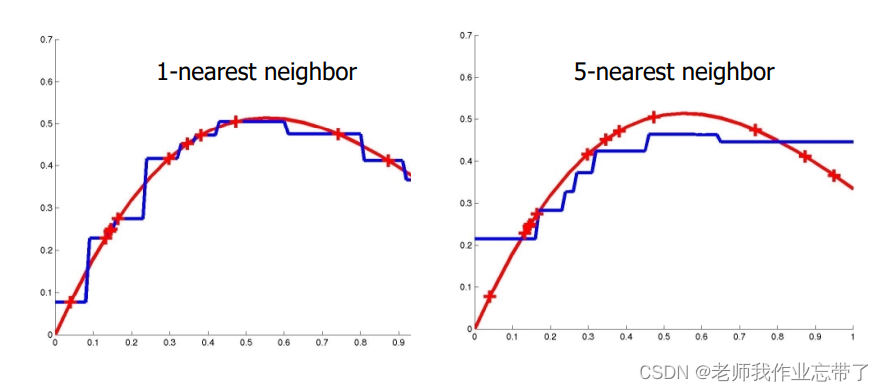
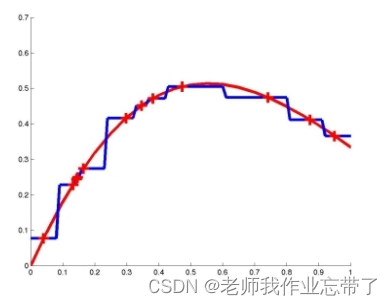
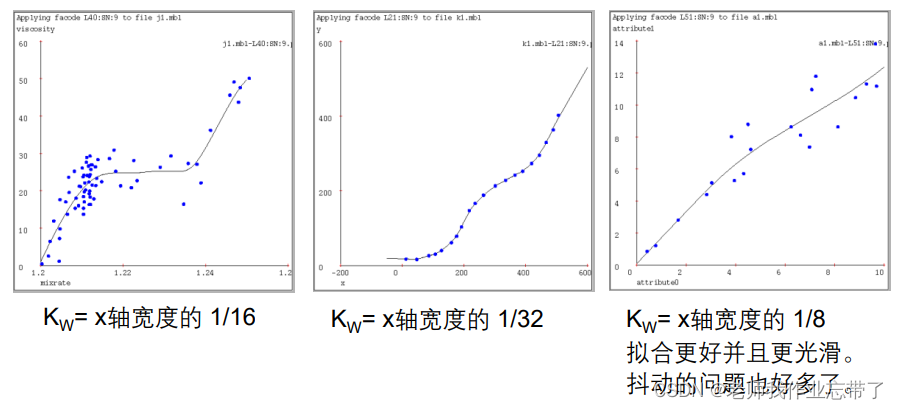
六、真实测试样例下 不同基于实例的算法表现举例
线性回归:
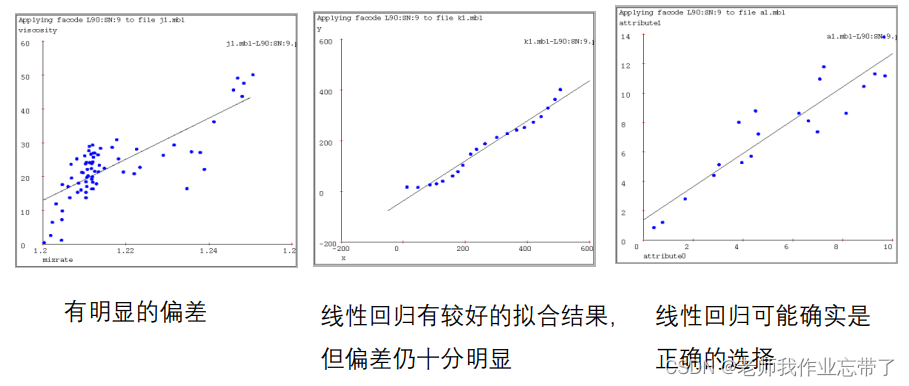
连接所有点
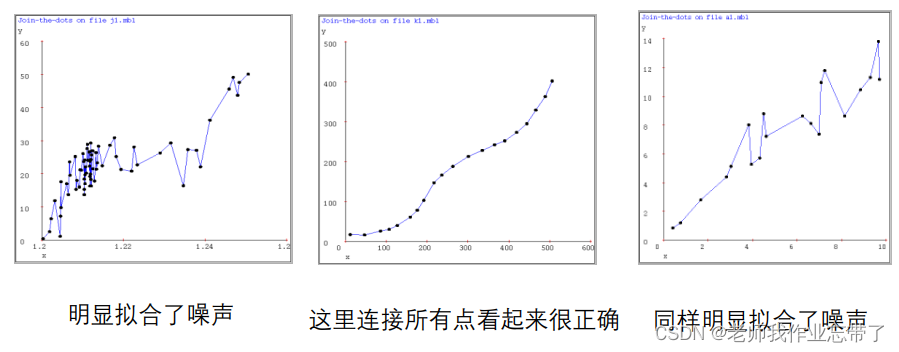
1-近邻
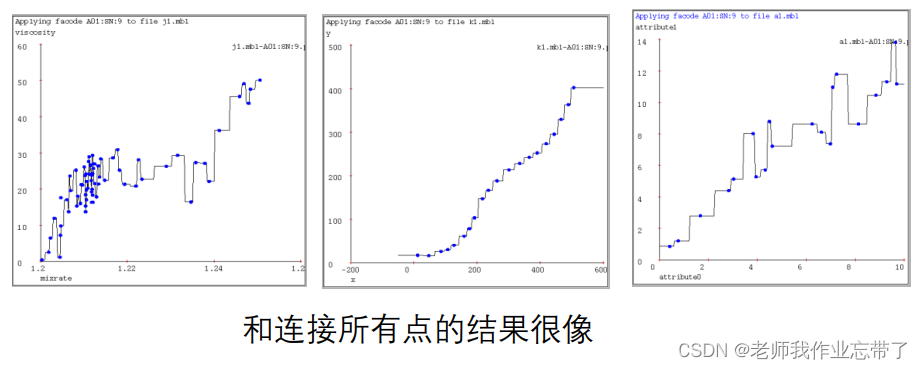
k-近邻(k=9)
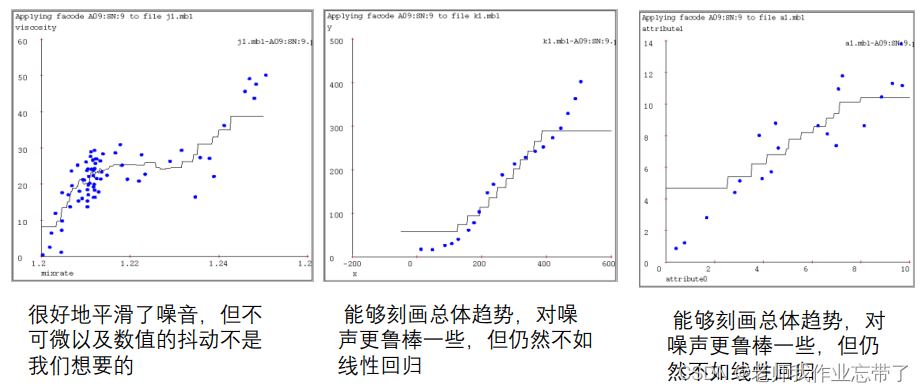
距离加权 KNN(核回归)
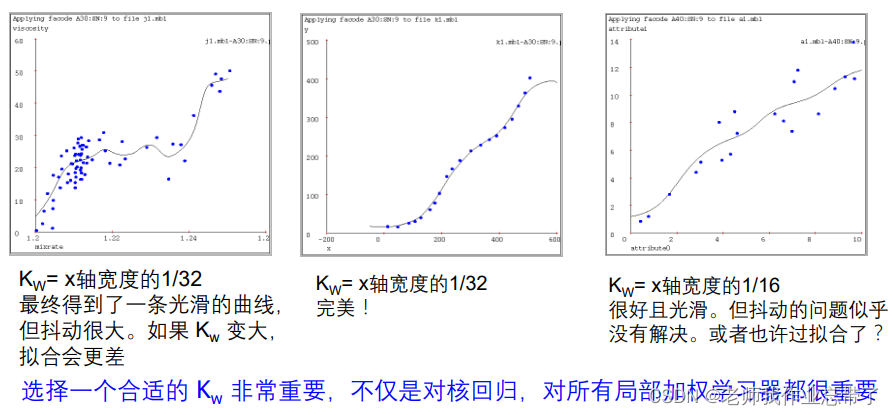
局部加权回归
七、懒惰学习与贪婪学习
Lazy learner and Eager Learner
懒惰学习 vs. 贪婪学习
