【数据结构】最小瓶颈路加强版（Kruskal重构树&RMQ求LCA）

题目描述

给定一个 n 个点 m 条边的无向连通图，编号为 1 到 n ，没有自环，可能有重边，每一条边有一个正权值 w 。
给出 q 个询问，每次给出两个不同的点 u 和 v ，求一条从 u 到 v 的路径上边权的最大值最小是多少。

输入格式

输入第一行两个整数 n, m。

接下来 m 行，每行三个整数 ai, bi, wi (ai != bi)，表示一条边 (ai, bi)，边权为 wi。

接下来一行一个整数 q，表示询问数量。

接下来一行四个整数 A,B,C,P，表示询问的生成方式。

由于本题数据规模较大，直接输入输出会占用比计算多数倍的时间，因此对询问的输入输出进行了压缩。

输入压缩方法是：读入4个整数 A,B,C,P，每次询问调用以下函数生成 u 和 v：

int A,B,C,P;
inline int rnd(){return A=(A*B+C)%P;}

每次询问时的调用方法为：

u=rnd()%n+1,v=rnd()%n+1;

若u和v相等则答案为0。

数据保证 0<=A<P，0<=C<P，P(B+1)<2^31-1

输出格式

输出共一行一个整数，表示所有询问的答案之和模 1000000007 的值。

由于本题数据规模较大，直接输入输出会占用比计算多数倍的时间，因此对询问的输入输出进行了压缩。

输出压缩方法是：输出所有询问的答案之和模 1000000007 的值。

样例

输入

5 7
1 2 8
2 3 9
3 1 2
3 4 7
1 4 4
3 5 6
1 4 9
10
233 17 66666 19260817

输出

32

数据范围与提示

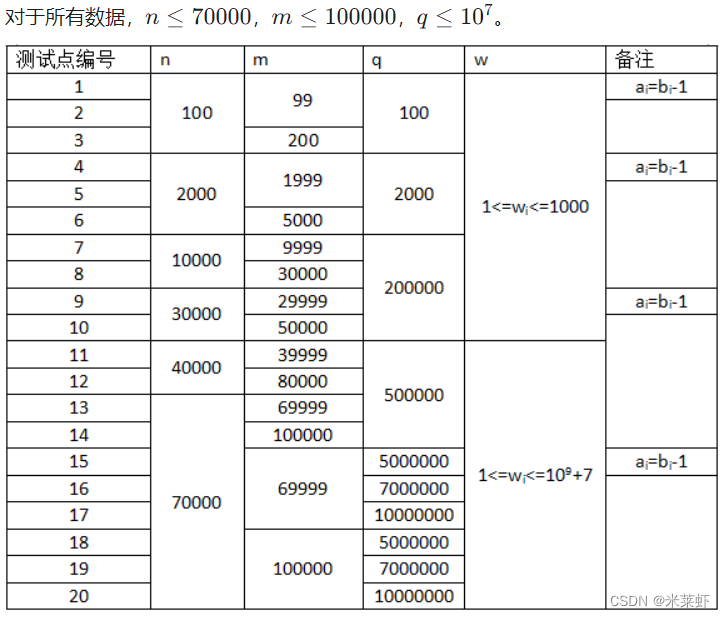
思路

首先可以证明，两点之间边权最大值最小的路径一定是在最小生成树上。考虑到这题是边权的最大值，直接把重构树建出来，然后查LCA处的权值即可。由于输入文件过大，需要用RMQ算法求LCA。

AC_Code

#include <bits/stdc++.h>
const int MAXN=1e6+10, mod=1e9+7;
using namespace std;

inline int read() {
    char c=getchar();
    int x=0, f=1;
    while (c<'0' || c>'9') {
        if(c=='-')    f=-1;
        c=getchar();
    }
    while (c>='0' && c<='9')  x=x*10+c-'0', c=getchar();
    return x*f;
}

int N,M,fa[MAXN],tot,val[MAXN],id[MAXN][21],num,dfn[MAXN],dep[MAXN],lg2[MAXN];

struct Edge {
    int u, v, w;
    bool operator<(const Edge &rhs) const { return w < rhs.w; }
} E[MAXN];

vector<int> v[MAXN];

int find(int x) {return fa[x]==x?fa[x]:fa[x]=find(fa[x]);}

void Kruskal() 
{
    for (int i=1; i<=2*N; i++)  fa[i]=i;
    tot = N;
    for(int i=1; i<=M; i++) {
        int x = find(E[i].u), y = find(E[i].v);
        if(x==y)    continue;
        val[++tot] = E[i].w;
        v[tot].push_back(x);
        v[tot].push_back(y);
        v[x].push_back(tot);
        v[y].push_back(tot);
        fa[x] = tot;
        fa[y] = tot;
    }
}

void dfs(int x, int fa) 
{
    dfn[x] = ++num;
    dep[x] = dep[fa]+1;
    id[num][0] = x;
    for (int i=0, to; i<v[x].size(); i++) {
        if((to=v[x][i])==fa)    continue;
        dfs(to, x);
        id[++num][0] = x;
    }
}

void RMQ() {
    for(int i=2; i<=num; i++)  lg2[i] = lg2[i>>1] + 1;
    for(int j=1; j<=20; j++)
        for(int i=1; i+(1<<j)-1<=num; i++) {
            int r = i+(1<<(j-1));
            id[i][j] = (dep[id[i][j-1]] < dep[id[r][j-1]]) ? id[i][j-1] : id[r][j-1];
        }
}

int A, B, C, P;
inline int rnd() { return A = (A*B+C) % P; }

int LCA(int x, int y) {
    x = dfn[x];
    y = dfn[y];
    if (x > y)
        swap(x, y);
    int k = lg2[y - x + 1];
    return dep[id[x][k]] < dep[id[y - (1 << k) + 1][k]] ? id[x][k] : id[y - (1 << k) + 1][k];
}

int main() {
    N = read();
    M = read();
    for (int i = 1; i <= M; i++) {
        int x = read(), y = read(), z = read();
        E[i] = (Edge){ x, y, z };
    }
    sort(E + 1, E + M + 1);
    Kruskal();
    dfs(tot, 0);
    RMQ();
    int ans = 0, Q = read();
    A = read();    B = read();
    C = read();    P = read();
    while (Q--) {
        int u = rnd() % N + 1, v = rnd() % N + 1;
        (ans += val[LCA(u, v)]) %= mod;
    }
    printf("%d", ans);
    return 0;
}