一.误差
1.误差与误差限
1.1 误差的分类
数值计算方法不研究模型误差和观测误差,其主要研究方法误差(截断误差)和舍入误差。
模型误差: 在将实际问题转化为数学模型的过程中,为了使数学模型尽量简单,以便于分析或计算,往往要忽略一些次要的因素,进行合理的简化。这样,实际问题与数学模型之间就产生了误差,这种误差称为模型误差,计算方法课中不讨论此种误差。
观测误差: 由于仪器本身的精度有限或某些偶然的客观因素会引入一定的误差,这种误差叫做观测误差,计算方法课中不讨论此种误差。
方法误差: 当实际问题的数学模型很复杂,不能获取模型的精确解,必须提供近似解,模型的准确解与数值方法准确解之差称为截断误差或方法误差。
舍入误差: 用有限位小数来代替无穷小数或用位数较少的小数来代替位数较多的有限小数所产生的误差。
1.2 绝对误差与绝对误差限
绝对误差(误差):绝对误差简称误差。设x是准确值,x*为x的一个近似值,则近似值x的绝对误差为e(x)。

绝对误差限:绝对误差的绝对值不超过某个正数ε,即|x-x*|≤ε,x落在[x-ε,x+ε]范围内。这个正数ε就是绝对误差限。

1.3 相对误差与相对误差限
相对误差:设x为准确值,x是近似值,e是近似值的绝对误差,则ε/x为该近似值的相对误差,记作er*。

相对误差限:相对误差的值不超过某个正数,即|(x-x*)/x|≤εr,这个正数εr就是相对误差限。

1.4 有效数字
如果x*近似表示x准确到小数后第n位,并从x *第n位起直到最左边的非零数字之间的一切数字都称为有效数字,并把有效数字的位数称为有效位数。

规格化形式:

有效数字与绝对误差的关系:

有效数字与相对误差的关系:

2.数值计算需要遵循的原则
i. 要使用数值稳定的算法,防止出现病态问题。
ii. 避免两个相似数相减,需进行等价变换。
iii. 绝对值太小的数不适合作为除数。
iv. 避免大数吃小数的现象。
v. 先化简再进行计算,避免误差的持续积累。
vi. 可以利用算法的递推性,简化结构并节省计算量。
二.插值与拟合

1.Lagrange插值
Lagrange插值公式的基本思想是把Pn(x)的构造问题转化为n+1个插值基函数li(x)(i=0,1,…,n)的构造。基函数构造完成后便可构造一个次数不超过n的插值多项式,并使之满足条件Pn(xi)=yi(i=0,1,2…)。


1.1 一阶线性Lagrange插值

一阶Lagrange插值称为一次线性Lagrange插值。其线性插值基函数和一次插值函数表达式分别为:


1.2 二阶抛物Lagrange插值

二阶Lagrange插值称为二次抛物Lagrange插值。其插值基函数和插值函数表达式分别为:


【例题】

【代码】
x=float(input())
def f(x):
return 3**x
# 二次Lagrange多项式插值
def Lagrange_2(x0,x1,x2,x):
l0 = ((x-x1)*(x-x2)) / ((x0-x1)*(x0-x2))
l1 = ((x-x0)*(x-x2)) / ((x1-x0)*(x1-x2))
l2 = ((x-x0)*(x-x1)) / ((x2-x0)*(x2-x1))
y = l0*f(x0)+l1*f(x1)+l2*f(x2)
return y
Y = Lagrange_2(0,1,2,x)
print("%.5f" % Y)
【测试】
1.33
4.53780
1.3 n阶Lagrange插值公式
由一阶二阶可以推广到n阶,n阶Lagrange插值公式如下:


数学公式看着太抽象了,还是结合题目写成代码易懂些。
【例题】

【代码】
from math import e,exp
print("请分别输入插值点x的值:")
# 输入x的值
listX = [float(num) for num in input().strip().split(" ")]
def f(x):
return e**(x**2-1)
# 获得对应的y值
def getlistY(listX):
listY=[]
for x in listX:
y=f(x)
listY.append(y)
return listY
# 获得l的值的函数,k为x的个数
def l(k,x,n):
sum=1
for i in range(n+1):
if i!=k:
sum *= (x-listX[i])/(listX[k]-listX[i])
return sum
# 求近似值的函数,n为Lagrange插值的阶数
def P(n,x):
listY = getlistY(listX)
sum = 0
for i in range(n+1):
sum += l(i,x,n)*listY[i]
return sum
print("请输入待估测值X:")
X=float(input())
# 分别输出不同阶的Lagrange插值近似值
for n in range(1,5):
print("%d阶Lagrange插值近似值为: %.4f" %(n,P(n,X)))
【测试】
请分别输入插值点x的值:
1.0 1.1 1.2 1.3 1.4
请输入待估测值X:
1.25
1阶Lagrange插值近似值为: 1.5842
2阶Lagrange插值近似值为: 1.7442
3阶Lagrange插值近似值为: 1.7557
4阶Lagrange插值近似值为: 1.7550
2.Newton插值
在学习Newton插值公式之前,我们需要先引入差商的概念。
我们从一阶差商看起:设有函数f(x)以及一系列互不相等的自变量x0, x1,…, xn(即在i≠ j时,xi ≠xj)的值 f(xi) , 称f[xi , xj]为f (x)在点xi , xj处的一阶差商。其计算公式为:

类推可知二阶差商的计算公式为:

则n阶差商公式为:

由差商的定义可知,高阶差商是两个低一阶差商的差商。一般我们用差商表来表示各阶差商的值。

【例题】

【代码】
x0,x1,x2,x3=map(float,input().split())
y0,y1,y2,y3=map(float,input().split())
# 计算一阶差商的函数
def f(X1,X2,Y1,Y2):
F = (Y1-Y2)/(X1-X2)
return F
# 一阶差商
F01 = f(x0,x1,y0,y1)
F12 = f(x1,x2,y1,y2)
F23 = f(x2,x3,y2,y3)
# 二阶差商
F02 = (F01-F12)/(x0-x2)
F13 = (F12-F23)/(x1-x3)
# 三阶差商
F03 = (F02-F13)/(x0-x3)
print("%d阶差商的值为:%.6f" %(1,F01))
print("%d阶差商的值为:%.6f" %(2,F02))
print("%d阶差商的值为:%.6f" %(3,F03))
【测试】
2 2.1 2.2 2.3
1.414214 1.449138 1.483240 1.516575
1阶差商的值为:0.349240
2阶差商的值为:-0.041100
3阶差商的值为:0.009167
当然,差商还可以通过更直观的均差表得出:(函数值为0阶均差)

经过一大坨复杂的数学证明,Newton插值多项式显然满足差商形式的插值条件。那么,我们可以由差商表得到Newton差商公式:




Newton插值公式相较于Lagrange插值公式有着巨大的优点,即其增加一个节点时,只需要再增加一项即可,没必要像Lagrange插值那样全部重新计算。
Newton插值公式的递推公式为:

【例题】
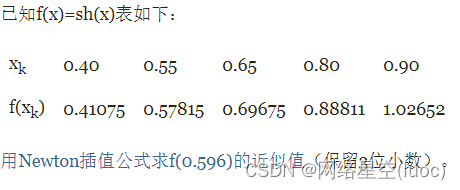
【代码】
print("请分别输入xk的值:")
x0,x1,x2,x3,x4=map(float,input().split())
print("请分别输入f(xk)的值:")
y0,y1,y2,y3,y4=map(float,input().split())
# 计算一阶差商的函数
def f(X1,X2,Y1,Y2):
F = (Y1-Y2)/(X1-X2)
return F
# 一阶差商
F01 = f(x0,x1,y0,y1)
F12 = f(x1,x2,y1,y2)
F23 = f(x2,x3,y2,y3)
F34 = f(x3,x4,y3,y4)
# 二阶差商
F02 = (F01-F12)/(x0-x2)
F13 = (F12-F23)/(x1-x3)
F24 = (F23-F34)/(x2-x4)
# 三阶差商
F03 = (F02-F13)/(x0-x3)
F14 = (F13-F24)/(x1-x4)
# 四阶差商
F04 = (F03-F14)/(x0-x4)
# 计算四阶Newton插值的函数
def Newton(x):
y = y0 + F01*(x-x0) + F02*(x-x0)*(x-x1) + F03*(x-x0)*(x-x1)*(x-x2) + F04*(x-x0)*(x-x1)*(x-x2)*(x-x3)
return y
print("请输入待估计的X的值:")
X = float(input())
Y = Newton(X)
print("利用四阶Newton插值公式计算出的f(X)结果为:%.3f" %Y)
【测试】
请分别输入xk的值:
0.40 0.55 0.65 0.80 0.90
请分别输入f(xk)的值:
0.41075 0.57815 0.69675 0.88811 1.02652
请输入待估计的X的值:
0.596
利用四阶Newton插值公式计算出的f(X)结果为:0.632
3.Hermite插值
在实际问题中,对于所构造的插值多项式,不仅要求函数值相等,而且要求其插值光滑,即要求节点处的导数值也相等。导数的阶数越高则光滑度越高。此类插值多项式称为Hermite插值多项式,也叫带导数的插值多项式。
Hermite插值满足的条件:

Hermite插值公式:

在实际情况中,我们最常使用的是两点三次Hermite插值,将n=1代入Hermite插值公式可得两点三次Hermite插值公式:

两点三次Hermite插值的基函数分别为:

为了便于理解,我们还是通过例题来体会Hermite插值算法。
【例题】

【代码】
print("请分别输入x的值:")
x0,x1=map(float,input().split())
print("请分别输入y的值:")
y0,y1=map(float,input().split())
print("请分别输入y'的值:")
y00,y11=map(float,input().split())
def Hermite(x0,x1,y0,y1,y00,y11,x):
L0 = (x-x1)/(x0-x1)
L1 = (x-x0)/(x1-x0)
F0 = ((1+2*L1)*y0 + (x-x0)*y00)
F1 = ((1+2*L0)*y1 + (x-x1)*y11)
H = F0*(L0**2) + F1*(L1**2)
return H
print("请输入待估测的X的值:")
X = float(input())
H = Hermite(x0,x1,y0,y1,y00,y11,X)
print("经两点三次Hermite插值得到的近似值为:%.5f" %H)
【测试】
请分别输入x的值:
1 2
请分别输入y的值:
0 0.693147
请分别输入y'的值:
1 0.5
请输入待估测的X的值:
1.5
经两点三次Hermite插值得到的近似值为:0.40907
4.分段插值与样条插值
对于代数插值来说,当插值多项式的次数很高时,逼近效果往往很不理想。其原因是,当n增大时,即节点加密时,f(x)与插值多项式的差别将会越来越大, 特别是在两端会发出激烈的振荡,这种现象叫龙格(Runge)现象。为了防止龙格现象的影响过大,我们要慎用高次插值,取而代之的是使用分段低次插值法。
所谓分段插值,就是将被插值函数分成几个小段,然后逐段多项式化。在各个子段上构造好插值多项式后,把它们装配到一起即可作为整个区间[a,b]上的插值函数。
在实际的工业生产中要求插值曲线既要尽可能简单,又要在曲线的连接处比较光滑。即这样的分段插值函数在分段上要求多项式次数低,还要求在节点上连续且存在连续的低阶导数,我们把满足这样条件的插值函数称为样条插值函数。样条插值函数所对应的曲线称为样条曲线,其节点称为样点,这种插值方法也被称为样条插值。
样条插值虽然理解起来比较复杂,但在做了某些近似简化后,样条的数学模型只是分段的三次多项式曲线。
尽管三次样条函数S(x)与分段Hermite插值函数具有很多共同点,但三次样条与分段Hermite插值有着本质区别:三次样条函数S(x)自身是光滑的,除了两个端点外其不需要知道 f 的导数值;而分段Hermite插值则完全依赖于f 在所有插值点的导数值。

三次样条插值一定满足以下条件:

5.插值余项与误差估计
设R(x)为余项(截断误差),f(x)为函数准确值,P(x)为插值函数估计值,则误差R(x)的公式为:

由罗尔定理可以推出:


由此公式可以导出Lagrange插值、Newton插值、Hermite插值等插值公式的误差估计公式:
1.Lagrange插值的误差估计:

2.Newton插值的误差估计:

3.Hermite插值的误差估计:

易知两点三次Hermite插值的误差估计:

4.分段插值的误差估计:

6.曲线拟合
在科学实验和统计分析中,除了可以用插值逼近获得函数近似值,也可以使用曲线拟合的方法获得误差最小的近似函数。与误差较大的插值逼近不同,曲线拟合不需要经过所有数据节点,其适用于数据量较大且对误差要求较高的情况。
用几何来通俗地解释,曲线拟合便是用已知平面内的一组点确定一条曲线,使该曲线能在整体上刻画这组点的变化趋势而不需通过每个点,我们称这种方法为曲线拟合,所求出的曲线称为拟合曲线。

我们通常用“误差的平方和最小”这个准则来进行曲线拟合,这种方法也称为曲线拟合的最小二乘法。为了更好地表示曲线拟合的曲线拟合,我们需要引入线性代数中的向量内积。
设u,v为两个n维向量,则它们的内积(u,v)的表达式为:

内积有三个主要的性质:



设φk(x)为基函数,ak为待求的系数,则待求的拟合函数P(x)的表达式为:

我们可以把这个式子写成正规方程组的形式:


我们通常将基函数φm(x)取值为x^m,其中m=0,1,2…

是不是感觉很抽象?
没错,我也不是很懂。
所以我们还是得通过具体题目的代码来理解这个拟合的过程。
【例题】
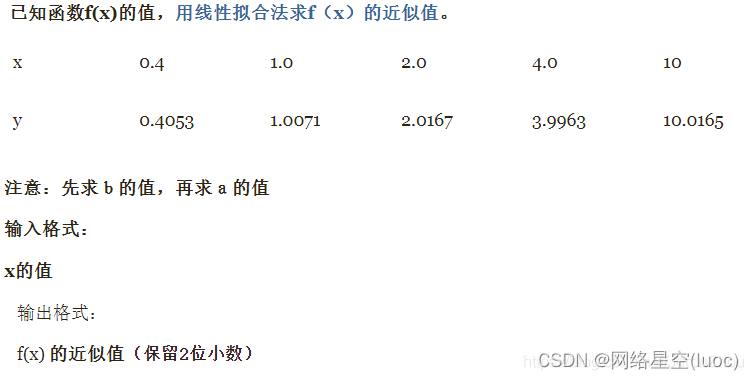
【代码】
import numpy as np
# 基函数向量
a0 = np.array([[1],[1],[1],[1],[1]]) # Φ0
a1 = np.array([[0.4],[1.0],[2.0],[4.0],[10]]) # Φ1
r = np.array([[0.4053],[1.0071],[2.0167],[3.9963],[10.0165]]) # r
b00 = b01 = b10 = b11 = r0 = r1 = 0
# 求矩阵元素值(内积)
for i in range(0,5):
b00 += a0[i]*a0[i] # (Φ0,Φ0)
b01 += a0[i]*a1[i] # (Φ0,Φ1)
b10 += a1[i]*a0[i] # (Φ1,Φ0)
b11 += a1[i]*a1[i] # (Φ1,Φ1)
r0 += a0[i]*r[i] # (Φ0,r)
r1 += a1[i]*r[i] # (Φ1,r)
# 解含有矩阵的方程,求出系数a,b的值
b = (r1*b00-r0*b10) / (b00*b11-b01*b10)
a = (r0-b01*b) / b00
print("请输入X的值:")
X = float(input())
Y = b*X+a
print("f(x)经拟合的近似值为:%.2f" % Y)
【测试】
请输入X的值:
1.33
f(x)经拟合的近似值为:1.34
三.数值微积分
1.梯形公式与中矩形公式
梯形公式:(两点,n=1时具有一次代数精度)


梯形公式的余项:
在这里插入图片描述
中矩形公式:


2.Simpson公式
Simpson公式(三点,n=2时具有三次代数精度):


Simpson公式的余项:

【例题】

【代码】
from math import e
print("请输入a,b的值:")
inp=input().split(' ')
a=float(inp[0])
b=float(inp[1])
def f(x):
y=(x**2)*(e**x)
return y
def Simpson(a,b):
y = (1/6)*(b-a)*(f(a)+4*f((a+b)/2)+f(b))
return y
Y = Simpson(a,b)
print("结果为:%.5f" % Y)
【测试】
请输入a,b的值:
0 1
结果为:0.72783
3.Cotes公式
Cotes系数表:
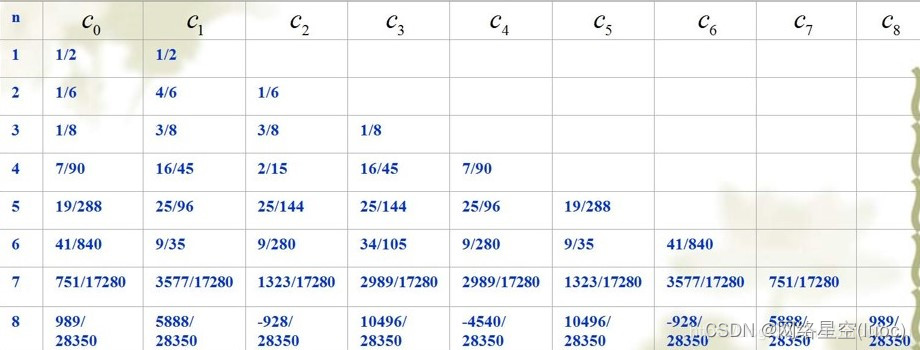
Cotes公式的余项:

当n为奇数时,Cotes公式具有n次代数精度;当n为偶数时,Cotes公式具有n+1次代数精度。
为了更高的精度,通常我们选取n=4时的Cotes公式使用,其具有五次代数精度:

【例题】

【代码】
from math import sin
print("请输入a,b的值:")
inp=input().split(' ')
a=float(inp[0])
b=float(inp[1])
def f(x):
if(x==0):
y=1
else:
y=sin(x)/x
return y
# n=4时的Cotes公式
def Cotes(a,b):
h = (b-a)/4
y = (b-a) * ((7/90)*f(a) + (16/45)*f(a+h) + (2/15)*f(a+2*h) + (16/45)*f(a+3*h) + (7/90)*f(b))
return y
Y = Cotes(a,b)
print("结果为:%.5f" % Y)
【测试】
请输入a,b的值:
0 1
结果为:0.94608
通过比较梯形公式、Simpson公式和Cotes公式的结果可以发现其精度依次上升。
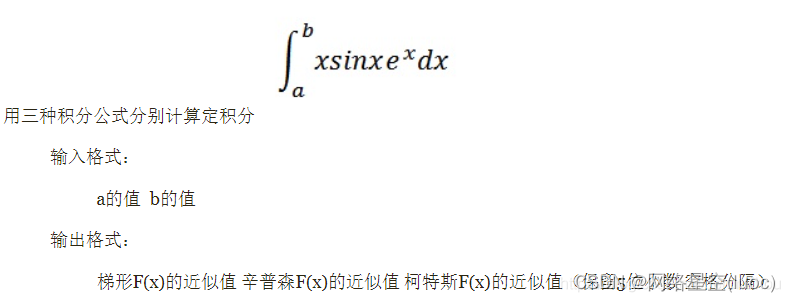
在这里插入图片描述
【代码】
from math import sin,e
print("请输入a,b的值:")
inp=input().split(' ')
a=float(inp[0])
b=float(inp[1])
def f(x):
y=x*sin(x)*(e**x)
return y
# 梯形公式
def Trapezoid(a,b):
y = (1/2)*(b-a)*(f(a)+f(b))
return y
# Simpson公式
def Simpson(a,b):
y = (1/6)*(b-a)*(f(a)+4*f((a+b)/2)+f(b))
return y
# Cotes公式
def Cotes(a,b):
h = (b-a)/4
y = (b-a) * ((7/90)*f(a) + (16/45)*f(a+h) + (2/15)*f(a+2*h) + (16/45)*f(a+3*h) + (7/90)*f(b))
return y
Y1 = Trapezoid(a,b)
Y2 = Simpson(a,b)
Y3 = Cotes(a,b)
print("梯形公式的结果为:%.5f" %Y1)
print("Simpson公式的结果为:%.5f" %Y2)
print("Cotes公式的结果为:%.5f" %Y3)
【测试】
请输入a,b的值:
0 1
梯形公式的结果为:1.14368
Simpson公式的结果为:0.64471
Cotes公式的结果为:0.64365
(梯形公式这误差有那么亿点点大啊。。。。)
4.复化求积公式
与插值类似,计算积分的时候也会出现龙格现象,故在次数过高时还是需要使用分段低阶的方法。
4.1 复化梯形公式
将求积区间分成n个小区间,之后在每个小区间上分别用梯形公式求积,再将结果累加起来,就可以得到复化梯形公式。
复化梯形公式的余项为:

复化梯形公式的算法如下:


【例题】

【代码】
from math import log
print("请分别输入a,b,n的值:")
inp=input().split(' ')
a = float(inp[0])
b = float(inp[1])
n = int(inp[2])
def f(x):
return log(x)
# 复化梯形公式
def Complex_Trapezoid(a,b,n):
h = (b-a)/n # 步长
T = 0
for i in range(1,n):
T += f(a+i*h)
y = (h/2)*(f(a)+2*T+f(b))
return y
Y = Complex_Trapezoid(a,b,n)
print("结果为:%.5f" % Y)
【测试】
请分别输入a,b,n的值:
3.2 5 6
结果为:2.52426
4.2 复化Simpson公式
复化Simpson公式:

复化Simpson公式的余项为:

复化Simpson公式的算法如下:


【例题】

【代码】
from math import sin,sqrt
print("请分别输入a,b,n的值:")
inp=input().split(' ')
a = float(inp[0])
b = float(inp[1])
n = int(inp[2])
def f(x):
y = sqrt(4-(sin(x)**2))
return y
# 复化Simpson公式
def Complex_Simpson(a,b,n):
h = (b-a)/n # 步长
x = a+(h/2)
S1 = f(x)
S2 = 0
for i in range(1,n):
S1 += f(a+i*h+h/2)
S2 += f(a+i*h)
S = (h/6)*(f(a)+4*S1+2*S2+f(b))
return S
Y = Complex_Simpson(a,b,n)
print("结果为:%.5f" % Y)
【测试】
请分别输入a,b,n的值:
0.5 1.1 7
结果为:1.11997
4.3 复化Cotes公式
【例题】

【代码】
print("请输入a,b的值:")
inp = input().split(' ')
a = float(inp[0])
b = float(inp[1])
n = 5
def f(x):
return 1/(x**2+x**4)
# 复化Cotes公式
def Complex_Cotes(a,b,n):
h = (b-a)/n
sum0 = sum1 = sum2 = sum3 = sum4 = 0
for i in range(1,n):
sum0 += f(a+i*h)
for i in range(0,n):
sum1 += f(a+i*h+h/5)
sum2 += f(a+i*h+2*h/5)
sum3 += f(a+i*h+3*h/5)
sum4 += f(a+i*h+4*h/5)
return (h/288)*(19*f(a)+19*f(b)+38*sum0+75*sum1+50*sum2+50*sum3+75*sum4)
Y = Complex_Cotes(a,b,n)
print("结果为:%.4f" %Y)
【测试】
请输入a,b的值:
0.8 1
结果为:0.1393
5.变步长梯形公式
变步长的梯形求积算法的实现步骤:


【例题】

【代码】
import math
print("请分别输入a,b的值:")
inp = input().split(' ')
a = float(inp[0])
b = float(inp[1])
e = 0.0001 # 误差
def f(x):
if(x==0):
return 1
else:
return 1/(x**2+x**4)
h = b-a
T1 = (h/2)*(f(b)+f(a))
# 变步长梯形求积
while True:
s = 0
x = a+h/2
while(x<b):
s = s+f(x)
x = x+h
T2 = T1/2+h/2*s
if(math.fabs(T2-T1)<e):
break
else:
h = h/2
T1 = T2
print("结果为:%.2f" % T2)
【测试】
请分别输入a,b的值:
1.2 2.4
结果为:0.12
6.Romberg公式
Romberg求积法的基本思想是通过低阶的公式组合成高阶公式。在变步长的过程中运用Romberg公式,就能将粗糙的梯形值Tn逐步加工成精度较高的Simpson值Sn、Cotes值Cn和Romberg值Rn;或者说,将收敛缓慢的梯形值序列Tn加工成收敛迅速的Romberg值序列Rn,这种加速方法称为Romberg算法。
Romberg公式:

Romberg求积算法的步骤如下:

【例题】

【代码】
print("请输入a,b的值:")
inp = input().split(' ')
a = float(inp[0])
b = float(inp[1])
def f(x):
return 4/(1+x**2)
# Romberg求积算法
def Romberg(a,b):
# 步长
# h1 = (b-a)/2
h2 = (b-a)/4
h3 = (b-a)/8
h4 = (b-a)/16
h5 = (b-a)/32
# 梯形公式
# T1 = (f(a)+f(b))/2
# T2 = T1/2+f(a+h1)/2
T4 = T2/2+(f(a+h2)+f(a+3*h2))/4
T8 = T4/2+(f(a+h3)+f(a+3*h3)+f(a+5*h3)+f(a+7*h3))/8
T16 = T8/2+(f(a+h4)+f(a+3*h4)+f(a+5*h4)+f(a+7*h4)+f(a+9*h4)+f(a+11*h4)+f(a+13*h4)+f(a+15*h4))/16
T32 = T16/2+(f(a+h5)+f(a+3*h5)+f(a+5*h5)+f(a+7*h5)+f(a+9*h5)+f(a+11*h5)+f(a+13*h5)+f(a+15*h5)+f(a+17*h5)+f(a+19*h5)+f(a+21*h5)+f(a+23*h5)+f(a+25*h5)+f(a+27*h5)+f(a+29*h5)+f(a+31*h5))/32
# Simpson公式
# S2 = (4/3)*T4-(1/3)*T2
S4 = (4/3)*T8-(1/3)*T4
S8 = (4/3)*T16-(1/3)*T8
S16 = (4/3)*T32-(1/3)*T16
# Cotes公式
# C2 = (16/15)*S4-(1/15)*S2
C4 = (16/15)*S8-(1/15)*S4
C8 = (16/15)*S16-(1/15)*S8
# Romberg公式
# R2 = (64/63)*C4-(1/63)*C2
R4 = (64/63)*C8-(1/63)*C4
return (b-a)*R4
Y = Romberg(a,b)
print("R4的结果为:%.2f" %Y)
【测试】
请输入a,b的值:
0 1
R4的结果为:3.14
7.Gauss求积公式
从数学证明中我们可以了解到n+1个节点的Gauss求积公式具有最高不超过2n+1次的代数精度,若如下插值求积公式具有2n+1次代数精度,则称之为Gauss求积公式,并称相应的求积节点为Gauss点.。
Gauss求积公式:

Gauss求积公式的构造方法:

几种常见的Gauss求积公式:

7.1 Gauss-Legendre求积公式
Gauss-Legendre公式的适用区间为[-1,1],如果积分区间不是[-1,1],则需要经过变换才能使用。
若积分区间为[a,b],则变换为标准形式的方法为:


我们最常用的是两点和三点Gauss-Legendre公式:
两点公式:

三点公式:

设xk为点的横坐标,Ak为f(xk)的前面的系数,则Gauss-Legendre公式的节点数n(两点公式的n=1,三点公式的n=2)和系数之间的对应表如下:


【例题】

【代码】
from math import sqrt
print("请输入a,b的值:")
inp = input().split(' ')
a = float(inp[0])
b = float(inp[1])
def f(x):
return sqrt(x+1.5)
# Gauss-Legendre求积公式
def Gauss_Legendre(a,b):
Gauss_Three = {
0.7745966692: 0.555555556, 0: 0.8888888889} # n=2时的系数
Sum = 0
for key, value in Gauss_Three.items():
Sum += f(((b-a)*key+a+b)/2)*value
if(key>0):
Sum += f(((a-b)*key+a+b)/2)*value
Sum = Sum*(b-a)/2
return Sum
Y=Gauss_Legendre(a,b)
print("结果为:%.5f" % Y)
【测试】
请输入a,b的值:
-1 1
结果为:2.39971
7.2 Gauss-Chebyshev求积公式
n+1次Chebyshev多项式的零点Xk的值为:

以Xk为Gauss点,结合此Gauss点的基函数Lk(x),可得出系数Ak的值为:

Gauss-Chebyshev求积公式为:

常用的有n=1和n=2时的Gauss-Chebyshev求积公式:


【例题】

【代码】
from math import sqrt,cos,pi,e
print("请输入高斯点的个数n:")
N = int(input())
def f(x):
return e**x
# Gauss-Chebyshev求积公式
def Gauss_Chebyshev(N):
n = N+1
x = [cos(pi*(2*k-1)/(2*n)) for k in range(1,n+1)]
op = (pi/n)*sum([f(x[k]) for k in range(0,n)])
return op
y=Gauss_Chebyshev(N)
print("结果为:%.6f" % y)
【测试】
请输入高斯点的个数n:
4
结果为:3.977463
8.数值微分
8.1 两点公式
向前差商公式:

向后差商公式:

中间差商公式:

【例题】

【代码】
from math import sin
print("请输入x的值:")
x = float(input())
def F(x):
return sin(x)/x
# 向前差商公式
def forword(x):
h = 1
t = 0
while(h>0):
f = (F(x+h)-F(x))/h
if(abs(f-t) < 0.001):
break
else:
t = f
h = h/2
return t
# 向后差商公式
def backword(x):
h = 1
t = 0
while (h > 0):
f = (F(x) - F(x-h)) / h
if (abs(f - t) < 0.001):
break
else:
t = f
h = h / 2
return t
# 中间差商公式
def middle(x):
h = 1
t = 0
while (h > 0):
f = (F(x+h) - F(x-h)) / (2*h)
if (abs(f - t) < 0.001):
break
else:
t = f
h = h / 2
return t
y1=forword(x)
y2=backword(x)
y3=middle(x)
print("向前差商公式的结果为:%.3f" %y1)
print("向后差商公式的结果为:%.3f" %y2)
print("中间差商公式的结果为:%.3f" %y3)
【测试】
请输入x的值:
4.1
向前差商公式的结果为:-0.090
向后差商公式的结果为:-0.093
中间差商公式的结果为:-0.092
8.2 三点公式
三点公式:



【例题】

【代码】
# 年份
print("请分别输入年份:")
inp1 = input().split(' ')
year1 = float(inp1[0])
year2 = float(inp1[1])
year3 = float(inp1[2])
year4 = float(inp1[3])
year5 = float(inp1[4])
year6 = float(inp1[5])
year7 = float(inp1[6])
year8 = float(inp1[7])
year9 = float(inp1[8])
year10 = float(inp1[9])
# 人口
print("请分别输入人口数:")
inp2 = input().split(' ')
population1 = float(inp2[0])
population2 = float(inp2[1])
population3 = float(inp2[2])
population4 = float(inp2[3])
population5 = float(inp2[4])
population6 = float(inp2[5])
population7 = float(inp2[6])
population8 = float(inp2[7])
population9 = float(inp2[8])
population10 = float(inp2[9])
h = 10
# 三点公式求增长率
rate1 = (1/(2*h))*(-3*population1+4*population2-population3)
rate2 = (1/(2*h))*(-population1+population3)
rate3 = (1/(2*h))*(-population2+population4)
rate4 = (1/(2*h))*(-population3+population5)
rate5 = (1/(2*h))*(-population4+population6)
rate6 = (1/(2*h))*(-population5+population7)
rate7 = (1/(2*h))*(-population6+population8)
rate8 = (1/(2*h))*(-population7+population9)
rate9 = (1/(2*h))*(-population8+population10)
rate10 = (1/(2*h))*(population8-4*population9+3*population10)
print("增长率分别为:%.3f %.3f %.3f %.3f %.3f %.3f %.3f %.3f %.3f %.3f" %(rate1,rate2,rate3,rate4,rate5,rate6,rate7,rate8,rate9,rate10))
【测试】
请分别输入年份:
1900 1910 1920 1930 1940 1950 1960 1970 1980 1990
请分别输入人口数:
76 92 106.5 123.2 131.7 150.7 179.3 204 226.5 251.4
增长率分别为:1.675 1.525 1.560 1.260 1.375 2.380 2.665 2.360 2.370 2.610
四.非线性方程
非线性方程包括了高次代数方程和超越方程,使用常规方法解非线性方程比较困难,想要用计算机解非线性方程只能使用特殊的算法。
1.二分法
二分法是解非线性方程组的重要方法,我们在中学就已经接触了二分法解方程组的思想,二分法是求实根的近似计算中行之有效的最简单方法,易于在计算机上实现,且对于函数的性质要求不高,仅仅要求它在有根区间上连续,且区间端点的函数值异号即可。它的缺点是不能求偶数重根,也不能求复根,收敛速度与以为公比的等比数列相同,不算太快,因此一般在求方程近似根时,不太单独使用,常用它来为其它方法求方程近似根提供好的初始值。其步骤如下:

将上述文字转化为算法流程图:

二分法的误差估计为:

若给定了精度ε,则其二分次数n满足:

二分法的优缺点:

还是老样子,我们通过例题来理解二分法的算法思想。
【例题】

【代码】
from math import log
def f(x):
return x*log(x)-1
left = 0.5
right = 4
mid = (left+right)/2
k = 0
# 二分法解方程
while(abs(f(mid))>0.001):
mid = (left+right)/2
k += 1
if((right-left)>0.001 and f(mid)>0.001):
right = mid
elif((right-left)>0.001 and f(mid)<-0.001):
left = mid
elif((right-left)<=0.001 or abs(f(mid))<=0.001):
break
k += 1
result = mid
print("根为%.3f" %result)
print("二分次数为%d" %k)
【测试】
根为1.763
二分次数为12
2.迭代法
迭代法是数值计算中一种典型的重要方法,尤其是计算机的普遍使用,使迭代法的应用更为广泛。所谓迭代法就是用某种收敛于所给问题的精确解的极限过程,来逐步逼近的一种计算方法,从而可以用有限个步骤算出精确解的具有指定精度的近似解,简单说迭代法是一种逐步逼近的方法。
迭代法的算法思想如下:

迭代法的算法实现:

【例题】

【代码】
from math import log
def f(x):
return log(3*(x**2))
x = 3.5
# 迭代法解方程
while(True):
t = x
x = f(x)
if(abs(t-x)<=0.0001):
break
print("结果为:%.3f" %x)
【测试】
结果为:3.733
对于这道题,我们可以构造出两种迭代函数:x=ln(3*x^2) 和 x=sqrt((e^x)/3)。这两种迭代方法有着不同的效果和收敛情况。用matplotlib库可以绘制出图像。
【代码】
from math import log,sqrt,e
from matplotlib import pyplot as plt
x1 = []
for i in range(1,501):
xi = 0+1.0*i/100
x1.append(xi)
y1 = list(map(lambda x:log(3*(x**2)),x1)) # 第一种迭代公式
y2 = list(map(lambda x:sqrt((1/3)*(e**x)),x1)) # 第二种迭代公式
plt.plot(x1,y1,"-b",label="y=ln(3*x^2)") # 第一种迭代公式
plt.plot(x1,y2,"-g",label="y=√((e^x)/3)") # 第二种迭代公式
plt.plot(x1,x1,"-r",label="y=x")
plt.xlim(0,5)
plt.ylim(0,5)
plt.legend()
plt.show()
print(y1)
print(y2)
【图像】

迭代过程的收敛条件:
若迭代函数φ(x)在[a,b]上有连续的一阶导数,φ(x)∈[a,b],且存在正数L使得对于任意的x∈[a,b]都有|φ’(x)|≤L<1成立,则φ(x)在[a,b]上存在唯一的解x*,且对于任意的初值x0,迭代值收敛于x*。
通俗一点说就是:迭代函数在某区间内的值都位于该区间内,且其迭代函数的一阶导数在此区间内的值的绝对值一定都小于一个小于1的正数,则这个迭代序列收敛。
压缩映像原理:
若某迭代函数在某区间内的值都位于该区间内,且满足李普希斯条件:若对任意的x1,x2∈[a,b]都满足|φ(x1)-φ(x2)|≤L|x1-x2|,且李普希斯常数L∈[0,1]。则迭代方程在[a,b]上有唯一解x*,迭代数列收敛,L数值越小收敛越快,并且存在误差估计:

局部收敛性:
若迭代函数φ(x)在不动点x的邻域内存在连续导数,并且|φ’(x)|<1,则φ(x)在x邻域内具有局部收敛性。
收敛阶( p ):

若p=1,则为一阶收敛(线性收敛)。
若p=2,则为二阶收敛(平方收敛)。
若1<p<2,则为超线性收敛。
可见,收敛阶p值越大,其收敛速度越快。
3.Newton迭代法
Newton迭代法的前提是f’(x)≠0,其核心思想是将非线性方程线性化,以线性方程的解逼近非线性方程的解,其具有局部收敛性,且至少具有平方收敛速度。
Newton迭代法迭代公式:


Newton迭代法的几何意义:


Newton迭代法的计算步骤:


【例题】

【代码】
from math import sin,cos
e = 0.0001
x = 2
N = 500
# f(x)
def f(x):
return sin(x)-(x/2)**2
# f'(x)
def f_1(x):
return cos(x)-(x/2)
# 牛顿迭代公式
def Newton(x):
x = x-(f(x)/f_1(x))
return x
# 迭代循环
for i in range(0,N):
if(abs(x-Newton(x)<e)):
print("结果为:%.3f" %Newton(x))
break
else:
x = Newton(x)
【测试】
结果为:1.934
Newton迭代法的收敛速度:
设f(x*)=0,f’(x)≠0,则x是f(x)=0的单根。若在单根x附近存在连续的二阶导数f’’(x*),且初始值在单根x*附近时,,Newton迭代法具有平方收敛速度。
经过数学推导可知,Newton迭代法的收敛性完全依赖于x0的选取,x0要求初值充分接近根以保证其局部收敛性。
全局收敛性定理:

满足全局收敛性定理有以下四种情况:

利用迭代法求平方根:

4.弦截法
4.1 单点弦截法
单点弦截法迭代公式:

【例题】

【代码】
from math import sin
print("请输入a,b的值:")
inp = input().split(' ')
a = float(inp[0])
b = float(inp[1])
e = 0.0001
n =1
def f(x):
return x-sin(x)-1
# 单点弦截迭代法
def Single_Point(x0,x1):
return x1-((x1-x0)/(f(x1)-f(x0)))*f(x1)
# 迭代循环
while(True):
if(abs(b-Single_Point(a,b))<e):
b = b+e
print("结果为:%.4f,迭代次数:%d" %(b,n))
break
else:
b = Single_Point(a,b)
n = n+1
【测试】
请输入a,b的值:
1 2
结果为:1.9346,迭代次数:12
4.2 两点弦截法
两点弦截法迭代公式:

【例题】

【代码】
from math import e
a = 0.3
b = 0.8
E = 0.0001
x = 0
def f(x):
return x-(e**-x)
# 两点弦截迭代法
def Double_Point(x0,x1):
return x1-(f(x1)/(f(x1)-f(x0)))*(x1-x0)
# 迭代循环
for i in range(0,500):
if(abs(x-Double_Point(a,b))<E):
print("结果为:%.3f" % x)
break
else:
x = Double_Point(a,b)
a = b
b = x
【测试】
结果为:0.567
与Newton迭代法相比,单点弦截法的收敛速度一般是线性的,其低于Newton法。两点弦截法的收敛速度也是比较快的,接近Newton法,但需要提供两个初始值。通过证明可知,两点弦截法具有超线性收敛速度。
我们可以通过下面这个例题来体会三种迭代方法的收敛速度的差别:
【例题】

【代码】
print("请输入x0和x1的值:")
inp = input().split(' ')
x0 = float(inp[0])
x1 = float(inp[1])
t0 = x0
t1 = x1
e = 0.00001
n = 1
x = 0
# f(x)
def f(x):
return x**3-3*x-1
# f'(x)
def f_1(x):
return 3*(x**2)-3
# Newton迭代法
def Newton(x):
return x-(f(x)/f_1(x))
# 单点弦截迭代法
def Single_Point(x0,x1):
return x1-((x1-x0)/(f(x1)-f(x0)))*f(x1)
# 双点弦截迭代法
def Double_Point(x0,x1):
return x1-(f(x1)/(f(x1)-f(x0)))*(x1-x0)
print("\n")
print("Newton迭代法:")
# Newton迭代法迭代循环
for i in range(0,500):
if(abs(x0-Newton(x0))<e):
print("迭代结果:%.5f 迭代次数:%d" % (x0, n))
break
else:
x0 = Newton(x0)
print("迭代结果:%.5f 迭代次数:%d" % (x0, n))
n = n + 1
n = 1
x = 0
x0 = t0
x1 = t1
print("\n")
print("单点弦截法迭代法:")
# 单点弦截法迭代循环
for i in range(0,500):
if(abs(x1-Single_Point(x0,x1))<e):
x1 = x1 + e
print("迭代结果:%.5f 迭代次数:%d" %(x1,n))
break
else:
x1 = Single_Point(x0,x1)
print("迭代结果:%.5f 迭代次数:%d" %(x1,n))
n = n + 1
n = 1
x = 0
x0 = t0
x1 = t1
print("\n")
print("两点弦截法迭代法:")
# 两点弦截法迭代循环
for i in range(0,500):
if(abs(x-Double_Point(x0,x1))<e):
x = x + e
print("迭代结果:%.5f 迭代次数:%d" %(x,n))
break
else:
x = Double_Point(x0,x1)
x0 = x1
x1 = x
print("迭代结果:%.5f 迭代次数:%d" %(x,n))
n = n + 1
【测试】
请输入x0和x1的值:
1.5 3
Newton迭代法:
迭代结果:2.06667 迭代次数:1
迭代结果:1.90088 迭代次数:2
迭代结果:1.87972 迭代次数:3
迭代结果:1.87939 迭代次数:4
迭代结果:1.87939 迭代次数:5
单点弦截法迭代法:
迭代结果:1.66667 迭代次数:1
迭代结果:1.96933 迭代次数:2
迭代结果:1.84938 迭代次数:3
迭代结果:1.89032 迭代次数:4
迭代结果:1.87552 迭代次数:5
迭代结果:1.88077 迭代次数:6
迭代结果:1.87889 迭代次数:7
迭代结果:1.87956 迭代次数:8
迭代结果:1.87932 迭代次数:9
迭代结果:1.87941 迭代次数:10
迭代结果:1.87938 迭代次数:11
迭代结果:1.87939 迭代次数:12
迭代结果:1.87940 迭代次数:13
两点弦截法迭代法:
迭代结果:1.66667 迭代次数:1
迭代结果:1.76613 迭代次数:2
迭代结果:1.90130 迭代次数:3
迭代结果:1.87744 迭代次数:4
迭代结果:1.87935 迭代次数:5
迭代结果:1.87939 迭代次数:6
迭代结果:1.87940 迭代次数:7