Lu分解法的C语言实现

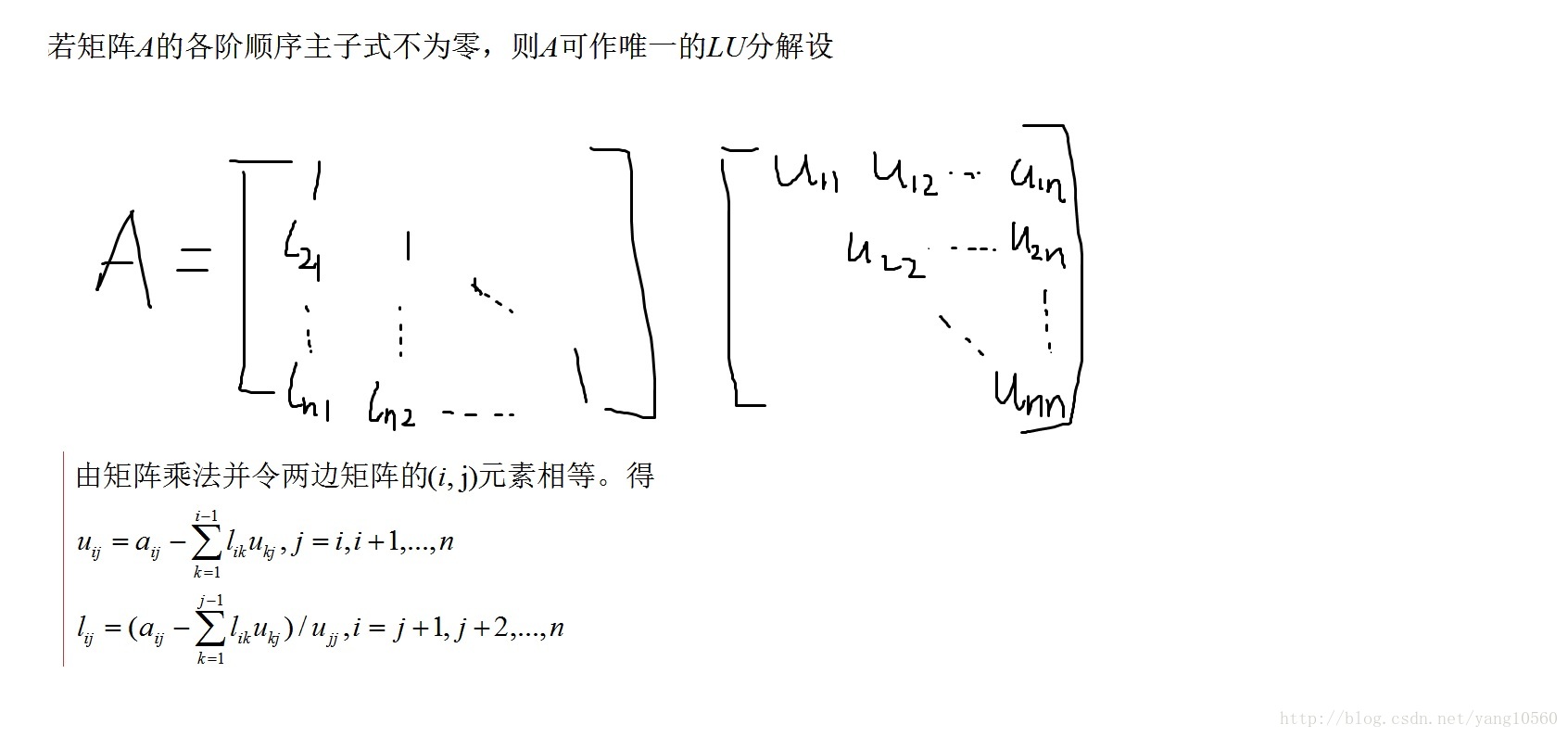
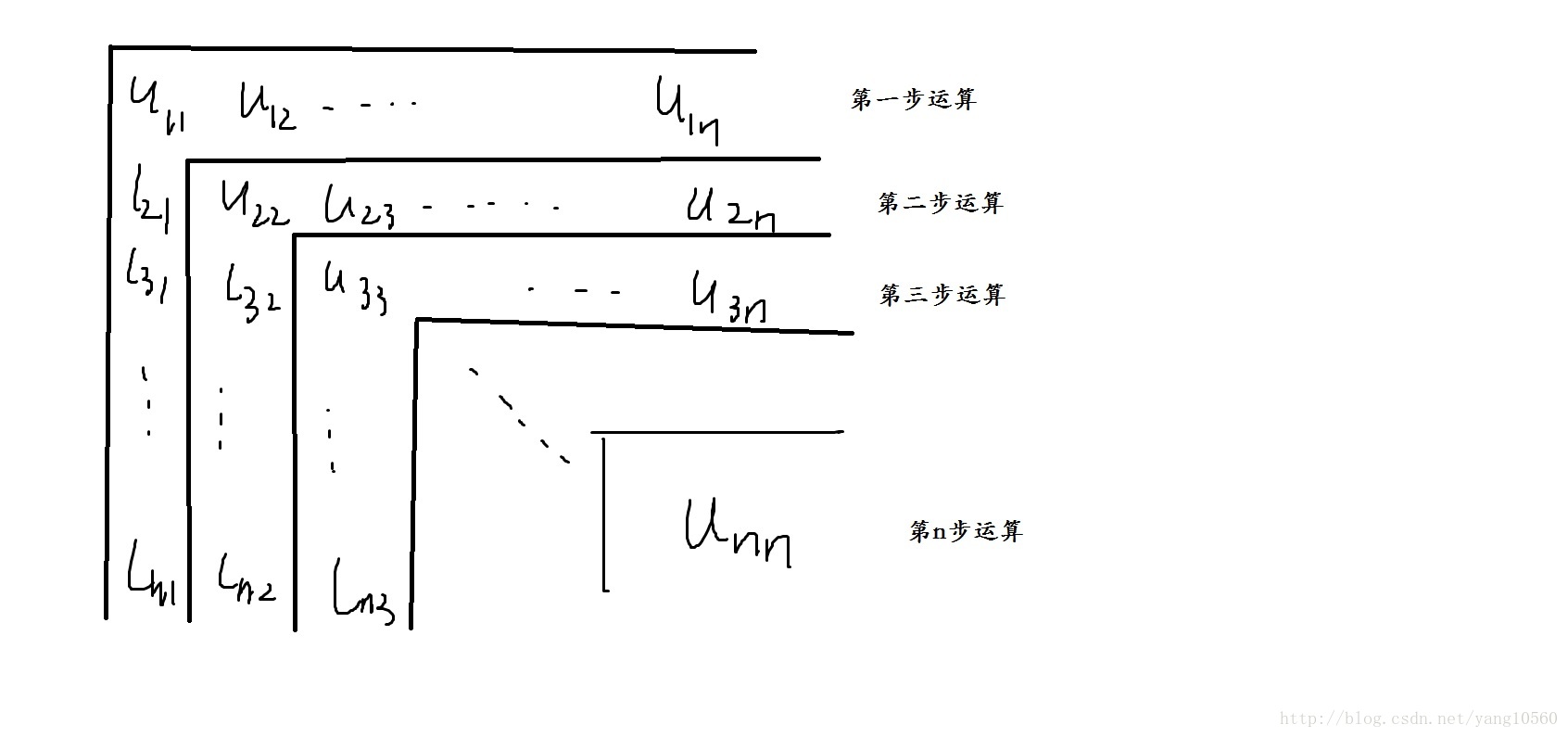
将系数矩阵A转变成等价两个矩阵L和U的乘积
，其中L和U分别是单位下三角矩阵和上三角矩阵。当A的所有顺序主子式都不为0时，矩阵A可以分解为A=LU（所有顺序主子式不为0，矩阵不一定不可以进行LU分解）。其中L是下三角矩阵，U是上三角矩阵。

LU分解在本质上是高斯消元法的一种表达形式。实质上是将A通过初等行变换变成一个上三角矩阵，其变换矩阵就是一个单位下三角矩阵。这正是所谓的杜尔里特算法（Doolittle algorithm）：从下至上地对矩阵A做初等行变换，将对角线左下方的元素变成零，然后再证明这些行变换的效果等同于左乘一系列单位下三角矩阵，这一系列单位下三角矩阵的乘积的逆就是L矩阵，它也是一个单位下三角矩阵。

–

构造矩阵A，b

                {1,2,3,4, }
    A=[         {1,4,2,-8,}
                {1,-1,4,1}   ]
                {1,3,5,2}

b = [14,-17,2,8]^T

代码实现：

#include <stdio.h>
#include <stdlib.h>
//LU分解法实现解线性方程组
//copyright @ Mryang

double sumU(double L[4][4] ,double U[4][4], int i, int j ){
    double sU = 0.0;
    for (int k = 1; k <= i-1 ; k++)
    {
        sU += L[i-1][k-1] * U[k-1][j-1];
    }

    return sU;
}//计算求和1

double sumL(double L[4][4] ,double U[4][4], int i, int j ){
    double sL = 0.0;
    for (int k = 0; k <= j-1; k++)
    {
        sL += L[i-1][k-1] * U[k-1][j-1];
    }

    return sL;

}//计算求和2

double sumY(double L[4][4] ,double y[4],int i){
    double sY=0.0;
    for (int k = 1; k <= i - 1; k++)
    {
        sY += L[i-1][k-1] * y[k-1];
    }
    return sY;
}//计算求和3

double sumX(double U[4][4] ,double x[4],int i ,int m){
    double sX = 0.0;
    for (int k = i+1; k <= m; k++)
    {
        sX += U[i-1][k-1] * x[k-1];
    }
    return sX;
}//计算求和4
int main(){

    double a[4][4] = { {1,2,3,1,},
                    {1,4,1,-1,},
                    {1,-1,-2,3,},
                    {1,3,-1,2}};//将系数存入二维数组
    double L[4][4] = {0};
    double U[4][4] = {0};//初始化部分
    double b[4] = {8,8,12,19};
    int n = 4;//n阶
    //输出[Ab]
    printf("[A]:\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%f\t", a[i-1][j-1]);
        }
        printf("\n");
    }

    //计算L,U
    for (int i = 1; i <= n; i++)
    {
        L[i-1][i-1] = 1;//对角线元素为1
        for (int j = i; j <= n; j++)
        {
            //由于数组下标从0开始 所以i-1,j-1
            U[i-1][j-1] = a[i-1][j-1] - sumU(L,U,i,j);

            if(j+1 <= n) L[j][i-1] = (a[j][i-1] - sumL(L,U,j+1,i))/U[i-1][i-1];//i变j+1，j变i 
        }

    }





    //输出U
    printf("U:\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%f\t",U[i-1][j-1]);
        }
        printf("\n");
    }
    //输出L
    printf("L:\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            printf("%f\t",L[i-1][j-1]);
        }
        printf("\n");
    }

    //由Ly=b 求y
    double y[4] = {0.0};
    y[0] = b[0];//y(1) = b(1);

    for (int i = 2; i <= n; i++)
    {
        y[i-1] = b[i-1] - sumY(L,y,i);
    }

    //由 Ux=y 求x
    double x[4] = {0.0};

    for (int i = n; i >= 1; i--)
    {
        x[i-1] =( y[i-1] - sumX(U,x,i,n))/ U[i-1][i-1];
    }



    //输出y
    printf("y:\n");
    for (int i = 0; i < n; i++)
    {
        printf("%f\n",y[i]);
    }
    printf("\n");
    //输出x
    printf("x:\n");
    for (int i = 0; i < n; i++)
    {
        printf("%f\n",x[i]);
    }
    printf("\n");
    system("pause");
    return 0;
}

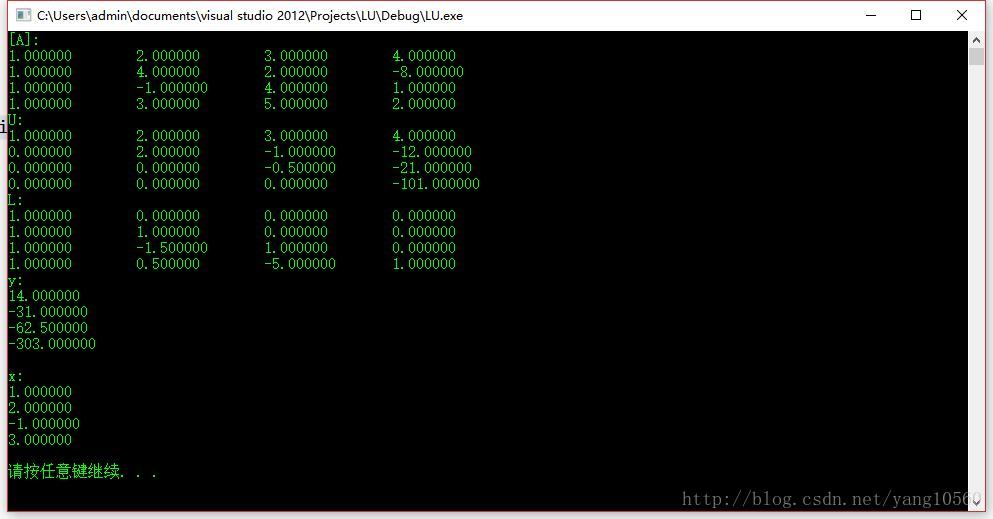
运行结果：

所以
x1=1
x2= 2
x3=-1
x4 = 3