文章目录
PCA
1. 简介
1.1 介绍
PCA(Principal Component Analysis) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。
1.2 数学准备
协方差
在一维空间中我们可以用方差来表示数据的分散程度。而对于高维数据,我们用协方差进行约束,协方差可以表示两个变量的相关性。为了让两个变量尽可能表示更多的原始信息,我们希望它们之间不存在线性相关性,因为相关性意味着两个变量不是完全独立,必然存在重复表示的信息。
协方差公式为:
C o v ( a , b ) = 1 m − 1 ∑ i = 1 m ( a i − μ a ) ( b i − μ b ) Cov(a,b)=\frac{1}{m-1}\sum_{i=1}^m(a_i-\mu_a)(b_i-\mu_b) Cov(a,b)=m−11i=1∑m(ai−μa)(bi−μb)
由于均值为 0,所以我们的协方差公式可以表示为:
C o v ( a , b ) = 1 m ∑ i = 1 m a i b i Cov(a,b)=\frac{1}{m}\sum_{i=1}^ma_ib_i Cov(a,b)=m1i=1∑maibi
当样本数较大时,不必在意其是 m 还是 m-1,为了方便计算,我们分母取 m。
协方差为 0 时,两个变量线性不相关。为了让协方差为 0,我们选择第二个基时只能在与第一个基正交的方向上进行选择,因此最终选择的两个方向一定是正交的。
协方差矩阵
针对我们给出的优化目标,接下来我们将从数学的角度来给出优化目标。
我们看到,最终要达到的目的与变量内方差及变量间协方差有密切关系。因此我们希望能将两者统一表示,仔细观察发现,两者均可以表示为内积的形式,而内积又与矩阵相乘密切相关。于是我们有:
假设我们只有 a 和 b 两个变量,那么我们将它们按行组成矩阵 X:
X = [ a 1 a 2 ⋯ a m b 1 b 2 ⋯ b m ] X=\begin{bmatrix}a_1&a_2&\cdots&a_m \\ b_1& b_2& \cdots &b_m \end{bmatrix} X=[a1b1a2b2⋯⋯ambm]
然后
1 m X X T = [ 1 m ∑ i = 1 m a i 2 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m a i b i 1 m ∑ i = 1 m b i 2 ] = [ C o v ( a , a ) C o v ( a , b ) C O v ( b , a ) C o v ( b , b ] \frac{1}{m}XX^T=\begin{bmatrix}\frac{1}{m}\sum_{i=1}^m a_i^2& \frac{1}{m}\sum_{i=1}^m a_ib_i \\ \frac{1}{m}\sum_{i=1}^m a_ib_i&\frac{1}{m}\sum_{i=1}^m b_i^2 \end{bmatrix} =\begin{bmatrix}Cov(a,a) &Cov(a,b) \\ COv(b,a)&Cov(b,b\end{bmatrix} m1XXT=[m1∑i=1mai2m1∑i=1maibim1∑i=1maibim1∑i=1mbi2]=[Cov(a,a)COv(b,a)Cov(a,b)Cov(b,b]
我们可以看到这个矩阵对角线上的分别是两个变量的方差,而其它元素是 a 和 b 的协方差。两者被统一到了一个矩阵里。
我们很容易被推广到一般情况:
设我们有m个n维数据记录,将其排列成矩阵 X n , m X_{n,m} Xn,m,设 C = 1 m X X T C=\frac{1}{m}XX^T C=m1XXT,则 C C C是一个对称矩阵,其对角线分别对应各个变量的方差,而第 i i i行 j j j列和 j j j行 i i i列元素相同,表示 i i i和 j j j两个变量的协方差
2. 流程
设有 m m m条 n n n维数据
1)将原始数据按列组成 n n n行 m m m列矩阵 X X X
2)将 X X X的每一行(代表一个属性字段) 进行零均值化,即减去每一行的均值
3)求出协方差矩阵 C = 1 m X X T C=\frac{1}{m}XX^T C=m1XXT
4)求出协方差矩阵的特征值及对应的特征向量
5) 将特征向量按对应特征值大小从上到下排列成矩阵,取前k组成矩阵 P P P
6) Y = P X Y=PX Y=PX即为降维到 k k k维后的数据
[ − 1 − 1 0 2 0 − 2 0 0 1 1 ] \begin{bmatrix}-1&-1&0&2&0 \\ -2&0&0&1&1\end{bmatrix} [−1−2−10002101]
为例,用PCA方法将这组二维数据降到一维。
因为这个矩阵的每一行已经是零均值,可以直接求协方差矩阵
C = 1 5 [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] [ − 1 − 2 − 1 0 0 0 2 1 0 1 ] = [ 6 5 4 5 4 5 6 5 ] C=\frac{1}{5}\begin{bmatrix}-1&-1&0&2&0 \\ -2&0&0&1&1\end{bmatrix} \begin{bmatrix}-1 &-2\\ -1&0 \\ 0&0 \\ 2&1 \\ 0&1\end{bmatrix} =\begin{bmatrix}\frac{6}{5} &\frac{4}{5} \\ \frac{4}{5}&\frac{6}{5} \end{bmatrix} C=51[−1−2−10002101]⎣⎢⎢⎢⎢⎡−1−1020−20011⎦⎥⎥⎥⎥⎤=[56545456]
然后求其特征值和特征向量,具体求解方法不再详述,可以参考相关资料。求解后特征值为
λ 1 = 2 , λ 2 = 2 5 \lambda_1=2,\lambda_2=\frac{2}{5} λ1=2,λ2=52
其对应的特征向量分别是
C 1 = [ 1 1 ] , C 2 = [ − 1 1 ] C_1=\begin{bmatrix}1\\ 1 \end{bmatrix},C_2=\begin{bmatrix} -1\\ 1\end{bmatrix} C1=[11],C2=[−11]
其中对应的特征向量分别是一个通解 c 1 c_1 c1和 c 2 c_2 c2可取任意实数,那么标准化后的特征向量为
C 1 = [ 1 2 1 2 ] , C 2 = [ − 1 2 1 2 ] C_1=\begin{bmatrix}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{bmatrix},C_2=\begin{bmatrix} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{bmatrix} C1=[2121],C2=[−2121]
因此我们的矩阵P是:
P = [ 1 2 1 2 − 1 2 1 2 ] P=\begin{bmatrix}\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}}\end{bmatrix} P=[21−212121]
可以验证协方差矩阵C的对角化
P C P T = [ 1 2 1 2 − 1 2 1 2 ] [ 6 5 4 5 4 5 6 5 ] [ 1 2 − 1 2 1 2 1 2 ] = [ 2 0 0 2 5 ] PCP^T=\begin{bmatrix}\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}\frac{6}{5}& \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt{2}} &-\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}}\end{bmatrix}=\begin{bmatrix}2&0 \\ 0 & \frac{2}{5}\end{bmatrix} PCPT=[21−212121][56545456][2121−2121]=[20052]
最后我们用P的第一行乘以数据矩阵,就得到了降维后的表示
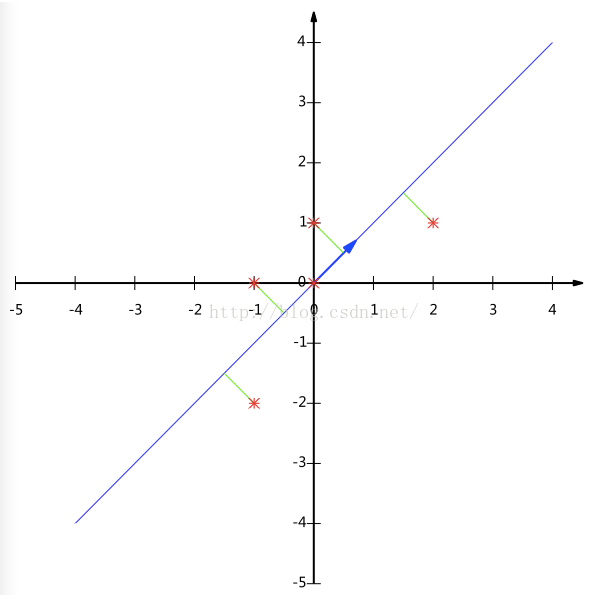
Y = [ 1 2 1 2 ] [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] = [ − 3 2 − 1 2 0 3 2 1 2 ] Y=\begin{bmatrix}\frac{1}{\sqrt{2}} &\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix}-1&-1&0&2&0 \\ -2&0&0&1&1\end{bmatrix}=\begin{bmatrix}-\frac{3}{\sqrt{2}} &-\frac{1}{\sqrt{2}}&0 &\frac{3}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix} Y=[2121][−1−2−10002101]=[−23−2102321]
降维投影结果如下图:
参考链接
人脸识别算法-特征脸方法(Eigenface)及python实现_不要说话的博客-CSDN博客_特征脸算法的实现过程
EigenFace的使用 python_u012005313的专栏-CSDN博客_eigenface python
3. 性质
- 缓解维度灾难:PCA 算法通过舍去一部分信息之后能使得样本的采样密度增大(因为维数降低了),这是缓解维度灾难的重要手段;
- 降噪:当数据受到噪声影响时,最小特征值对应的特征向量往往与噪声有关,将它们舍弃能在一定程度上起到降噪的效果;
- 过拟合:PCA 保留了主要信息,但这个主要信息只是针对训练集的,而且这个主要信息未必是重要信息。有可能舍弃了一些看似无用的信息,但是这些看似无用的信息恰好是重要信息,只是在训练集上没有很大的表现,所以 PCA 也可能加剧了过拟合;
- 特征独立:PCA 不仅将数据压缩到低维,它也使得降维之后的数据各特征相互独立;
4. 作业
ORL数据集 使用的数据集att_faces
由剑桥大学AT&T实验室创建,包含40人共400张面部图像,部分志愿者的图像包括了姿态,表情和面部饰物的变化。大小是92×112(Face recognition database, a total of 40 individuals, each person 10 images, size is 92×112)。
需要将文件划分为训练集和测试集,这里训练集包含28个文件夹,测试集包含12个,功能40个文件夹,对应40个人的图像。每个文件夹下有10张png格式图像文件,文件夹内均为同一人的面部图像。具体如下所示:

我自己上传的 ORL数据集attrface | Kaggle
别人的npy格式的ORLFaces | Kaggle
官网网址,貌似不能用了https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html
4.1 作业1 PCA 提取特征脸
我们要求的是 X X T XX^T XXT的特征值, X X T XX^T XXT是协方差矩阵,一个图片的 X X T XX^T XXT,维数可能是 d i m ( X X T ) = [ 256 ∗ 256 , 256 ∗ 256 ] dim(XX^T)=[256*256,256*256] dim(XXT)=[256∗256,256∗256],维数过大,不方便求特征向量???
首先我们看 X T X X^TX XTX的特征向量 ( X T X ) v i = λ i v i (X^TX)v_i=\lambda_iv_i (XTX)vi=λivi,为了方便计算,我们使用了 X X T XX^T XXT
X X T ( X v i ) = λ i ( X v i ) XX^T(Xv_i)=\lambda_i(Xv_i) XXT(Xvi)=λi(Xvi)
所以要求 X X T XX^T XXT的特征向量
- 求出 X T X X^TX XTX的特征向量 v i v_i vi
- X T X X^TX XTX的特征向量为 X v i Xv_i Xvi
4.2 作业二 Eigenface
经典PCA(Eigenface)和LDA(Fisherface)相继诞生
OpenCV: Face Recognition with OpenCV
特征脸EigenFace的思想是把人脸从像素空间变换到另一个空间,在另一个空间中做相似性的计算。EigenFace选择的空间变换方法是PCA,也就是大名鼎鼎的主成分分析。它广泛的被用于预处理中以消去样本特征维度之间的相关性。当然了,这里不是说这个。EigenFace方法利用PCA得到人脸分布的主要成分,具体实现是对训练集中所有人脸图像的协方差矩阵进行本征值分解,得对对应的本征向量,这些本征向量(特征向量)就是“特征脸”。每个特征向量或者特征脸相当于捕捉或者描述人脸之间的一种变化或者特性。这就意味着每个人脸都可以表示为这些特征脸的线性组合。
一组特征脸可以通过在一大组描述不同人脸的图像上进行主成分分析(PCA)获得。任意一张人脸图像都可以被认为是这些标准脸的组合。例如,一张人脸图像可能是特征脸1的10%,加上特征脸2的55%,在减去特征脸3的3%。值得注意的是,它不需要太多的特征脸来获得大多数脸的近似组合。另外,由于人脸是通过一系列向量(每个特征脸一个比例值)而不是数字图像进行保存,可以节省很多存储空间。
特征脸的应用:
特征脸的最直接的应用就是人脸识别。在这个需求下,特征脸相比其他手段在效率方面比较有优势,因为特征脸的计算速度非常快,短时间就可以处理大量人脸。但是,特征脸在实际使用时有个问题,就是在不同的光照条件和成像角度时,会导致识别率大幅下降。因此,使用特征脸需限制使用者在统一的光照条件下使用正面图像进行识别
1. 加载数据
import numpy as np
import os
import cv2
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from PIL import Image
suffix_list = ['.jpg', '.png', '.jpeg', '.JPG', '.PNG', '.JPEG']
m = 0
n = 0
def get_images():
global m, n
images = []
labels = []
root = r"lfw/lfw_funneled"
for index, dir in enumerate(os.listdir(root)):
path = os.path.join(root, dir)
for filename in os.listdir(path):
# 如果是图片的话
if os.path.splitext(filename)[1] in suffix_list:
img = np.array(Image.open(os.path.join(path, filename)).convert('L'), 'f')
# (250, 250)
m = img.shape[0]
n = img.shape[1]
images.append(img.flatten())
# 放置标签信息
labels.append(filename)
# 一共5749张图像,所以只取前500个人张图片
if index > 100:
break
return images, labels
def get_att_faces():
"""
准备数据
:return:
"""
image = []
y = []
global m, n
data_path = r"att_faces"
root_path = os.listdir(data_path)
for idx, d in enumerate(root_path):
s_path = os.path.join(data_path, d)
for image_path in os.listdir(s_path):
# 因为是二维图,所以是二维的 [112,92]
img = cv2.imread(os.path.join(s_path, image_path), cv2.IMREAD_GRAYSCALE)
m = img.shape[0]
n = img.shape[1]
# 取前K个特征
# 选取特征值K个最大特征值作为Sm_i的特征值
image.append(np.asarray(img).flatten())
y.append(idx)
return np.asarray(image), y
def get_test():
x = np.array([[-1, -2],
[-1, 0],
[0, 0],
[2, 1],
[0, 1]])
y = np.array([0, 0, 0, 0, 0])
return x, y
def show(image):
plt.figure("1")
plt.imshow(image.reshape(m, n), cmap="gray")
plt.axis('on') # 关掉坐标轴为 off
plt.show()
def show_image(x):
"""
展示特征图
:param x:
:return:
"""
fig, axes = plt.subplots(4, 6, figsize=(8, 4), subplot_kw={
"xticks": [], "yticks": []})
for i, ax in enumerate(axes.flat):
temp = x[:, i]
temp = temp.reshape(m, n)
temp = temp.clip(0, 255)
ax.imshow(np.rint(temp).astype('uint8'), cmap="gray")
# np.rint()是根据四舍五入取整,因为图片的值是整形的,矩阵求出的值是浮点型
plt.axis('on') # 关掉坐标轴为 off
plt.show()
2. 主成分分析
在求得的特征向量和特征值中,越大的特征值对于我们区分越重要,也就是我们说的主成分,我们只需要那些大的特征值对应的特征向量,
而那些十分小甚至为0的特征值对于我们来说,对应的特征向量几乎没有意义。在这里我们通过一个阈值selecthr来控制,当排序后的特征值的一部分相加
大于该阈值时,我们选择这部分特征值对应的特征向量,此时我们剩下的矩阵是11368*M’,M’根据情况在变化。 这样我们不仅减少了计算量,而且保留
了主成分,减少了噪声的干扰。
def calculate_covariance_matrix(x, selecthr=None):
"""
因为图片计算协方差矩阵非常的大,所以我们采取 另一种写法得到矩阵的
:param selecthr: 阈值,选取矩阵的多少特征
:param x:
:return:
"""
# 计算X^TX的特征向量和特征值
A = x.T.dot(x)
eigen_values, eigen_vectors = np.linalg.eig(A)
# 对特征向量进行排序,选择前70个特征先
idx = eigen_values.argsort()[::-1]
if selecthr is not None:
"""
不添加阈值,就是选取100%的特征
"""
# 选取selecthr%的特征作为向量
for i in range(x.shape[1]):
if (eigen_values[idx[:i]] / eigen_values.sum()).sum() >= selecthr:
idx = idx[:i]
break
w = eigen_vectors[:, idx]
return np.dot(x, w)
def train(x, y):
"""
训练加载好的数据
:param x:
:param y:
:return:
"""
global mean_x
x = np.asarray(x)
x = x.T
y = np.asarray(y)
# 计算所有图片的均值
mean_x = x.mean(axis=1).reshape(-1, 1)
# 得到中心化后的图片信息
diffTrain = x - mean_x
covVects = calculate_covariance_matrix(diffTrain, selecthr=0.9)
# 展示前24个特征脸
show_image(covVects[:, :24])
# 均值图像, 协方差矩阵的特征向量, diffTrain是偏差矩阵
return mean_x, covVects, diffTrain
3. 测试
def test(X_train, X_test, y_train, y_test, mean_x, covVects, ):
"""
进行测试
:return:
"""
X_train = X_train.T
X_test = X_test.T
print("训练集的维度", X_train.shape)
print("测试集的维度", X_test.shape)
print("协方差维度", covVects.shape)
w_train = covVects.T.dot(X_train - mean_x)
print("训练的w_train", w_train.shape)
w_predict = covVects.T.dot(X_test - mean_x)
print("测试的w_predict", w_predict.shape)
acc = 0
y_predict = []
for idx, predict_image in enumerate(w_predict.T):
temp = []
for train_image in w_train.T:
temp.append(np.linalg.norm(predict_image - train_image))
index = y_train[np.argmin(temp)]
if index == y_test[idx]:
print("预测正确,图片为第{}类".format(index))
acc += 1
else:
print("预测错误,预测为第{}类,因为是第{}类".format(index, y_test[idx]))
y_predict.append(index)
print("准确率为{}%--[{}/{}]".format(acc / len(y_predict) * 100, acc, len(y_predict)))
plt.rcParams['font.sans-serif'] = ['simHei']
plt.rcParams['axes.unicode_minus'] = False
# images, labels = get_test()
# images, labels = get_images()
X, y = get_att_faces()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
mean_x, covVects, diffTrain = train(X_train, y_train)
test(X_train, X_test, y_train, y_test, mean_x, covVects)
4. 结果
这个是第一题的结果

这个是第二题结果

参考链接
(1条消息) PCA人脸识别详解——初学者必看_xiaomage_gf的博客-CSDN博客_pca人脸识别
(1条消息) 用PCA、LDA、LR做人脸识别代码实现_Toby的博客-CSDN博客_lda进行人脸识别
https://blog.csdn.net/marleylee/article/details/81194998