一、图像形成概述

在分析和处理图像之前，需要建立一个描述场景几何形状的词汇表。还需要了解在给定一组光照条件、场景几何、表面特性和相机光学器件的情况下产生特定图像的图像形成过程。同时了解图像形成过程的简化模型。

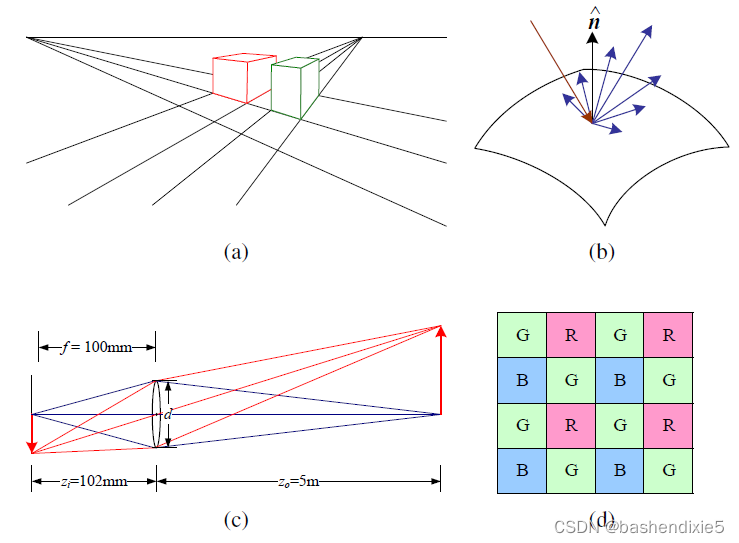
首先了解基本几何图元（点、线和平面）以及将这些 3D 量投影到 2D 图像特征的几何变换（图1-a）。然后再了解光照、表面属性（图1-b）和相机光学（图1-c）如何相互作用以产生落在图像传感器上的颜色值。继而知道连续彩色图像如何在图像传感器内部转换为离散数字样本（图 1-d），以及如何避免（或至少表征）采样缺陷，例如混叠。

图1 图像形成过程的几个组成部分：(a) 透视投影；(b) 撞击表面时的光散射； (c) 镜头光学； (d) 拜耳滤色片阵列。

二、几何图元和变换

首先需要了解2D和3D图元，即点、线和平面。接着了解如何将3D特征投影到2D特征中。

1、几何图元

几何图元构成了用于描述三维形状的基本构建块。

（1）2D points

二维点（图像中的像素坐标）可以用一对值表示， $X = (x, y) \in R^2$ ，或者 $X = \binom{x}{y}$ ，我们使用 $(x_1,x_2,......)$ 表示法来表示列向量。

二维点也可以使用齐次坐标表示， $\tilde{x} = (\tilde{x}, \tilde{y}, \tilde{w}) \in P^2$ ，其中仅在尺度上不同的向量被认为是等价的。 $P^2 = R^3 - (0, 0, 0)$ 称为二维射影空间。

齐次向量 $\tilde{x}$ 可以通过除以最后一个元素 $\tilde{w}$ 转换回非齐次向量 x，即 $\tilde{X} = (\tilde{x}, \tilde{y}, \tilde{w}) = \tilde{w}(x, y, 1) = \tilde{w} \bar{X}$ ，其中 $\bar{X} = (x, y, 1)$ 是增广向量。最后一个元素为 $\tilde{w} = 0$ 的齐次点称为理想点或无穷远处的点，它们没有等效的非齐次表示。

（2）2D lines

二维线也可以用齐次坐标表示 $\tilde{l} = (a, b, c)$ 。对应的线方程为 $\bar{X}\cdot \tilde{l} = ax + by + c = 0:$

我们可以对直线方程向量进行归一化，使得 $l = (\hat{n}_x, \hat{n}_y, d) = (\hat{n}, d)$ 其中 $\left \| \hat{n} \right \| = 1$ 。在这种情况下， $\hat{n}$ 是垂直于直线的法向量， $d$ 是它到原点的距离（图 2）。（这种归一化的一个例外是无穷远处的线 $\tilde{l} = (0,0,1)$ ，它包括无穷远处的所有（理想）点。）

图2 (a) 2D 线方程和 (b) 3D 平面方程，用法线 ^n 和到原点的距离 d 表示。

也可以将 $\hat{n}$ 表示为旋转角度 $\theta$ 的函数， $\hat{n} = (\hat{n}_x, \hat{n}_y) = (cos\theta , sin\theta )$ （图2-a）。这种表示通常用于霍夫变换寻线算法中，组合 $(\theta, d)$ 也称为极坐标。

当使用齐次坐标时，我们可以计算两条线的交点为 $\tilde{x} =\tilde{l}_1 \times \tilde{l}_2$ ，其中 $\times$ 是叉积算子。类似地，连接两点的线可以写成 $\tilde{l}= \tilde{x}_1 \times \tilde{x}_2$ ，当试图将一个交点拟合到多条线，或者相反，一条线到多点时，可以使用最小二乘法。

扫描二维码关注公众号，回复： 14175781 查看本文章

（3）2D conics

还有其他代数曲线可以用简单的多项式齐次方程表示。例如，圆锥截面（之所以这么称呼，是因为它们是平面和 3D 圆锥的交点）可以使用二次方程来编写 $\tilde{X}^T Q \tilde{X} = 0$ 。

二次方程在多视图几何和相机校准的研究中发挥了有用的作用。

（4）3D points

三维的点坐标可以用非齐次坐标 $X = (x, y, z) \in R^3$ 或齐次坐标 $\tilde{X} = (\tilde{x}, \tilde{y}, \tilde{z}, \tilde{w}) \in P^3$ 来写。

和以前一样，有时使用具有 $\tilde{X} = \tilde{w} \bar{X}$ 的增广向量 $x = (x, y, z, 1)$ 来表示 3D 点很有用。

（5）3D planes

3D 平面也可以表示为齐次坐标 $\tilde{m} = (a, b, c, d)$ 并带有相应的平面方程 $\bar{X} \cdot \tilde{m} = ax + by + cz + d = 0$ ，我们还可以将平面方程写作 $m = (\hat{n}_x, \hat{n}_y, \hat{n}_z, d) = (\hat{n}, d)$ 归一化，其中 $\left \| \hat{n} = 1 \right \|$ 。在这种情况下， $\hat{n}$ 是垂直于平面的法向量，并且 $d$ 是它到原点的距离（图2-b）。与 2D 线的情况一样，无穷远处的平面 $\tilde{m} = (0, 0, 0, 1)$ 包含无穷远处的所有点，不能归一化（即，它没有唯一的法线或有限距离）

我们可以将 $\hat{n}$ 表示为两个角度 $( \theta, \phi)$ 的函数， $\hat{n} = (cos\theta cos\phi, sin \theta cos \phi, sin \phi)$ 即，使用球坐标，但这些比极坐标更不常用，因为它们不能均匀地对可能的法向量空间进行采样。

（6）3D lines

3D 中的线条不如 2D 中的线条或 3D 中的平面那么优雅。一种可能的表示是使用线上的两个点 $(p, q)$ 。线上的任何其他点都可以表示为这两个点的线性组合 $r = (1 -\lambda )p +\lambda q$ ，如图3所示。如果我们限制 $0 \leq \lambda \leq 1$ ，我们得到连接 p 和 q 的线段。

如果我们使用齐次坐标，我们可以把这条线写成 $\tilde{r} = \mu \tilde{p} + \lambda \tilde{q}$

这种情况的一个特殊情况是当第二个点在无穷远处时，即 $\tilde{q} = (\hat{d}_x, \hat{d}_y, \hat{d}_z, 0) = (\hat{d}, 0)$ 。在这里，我们看到 $\hat{d}$ 是线的方向。然后我们可以将非齐次3D line方程重写为 $r = p + \lambda \hat{d}$

3D 线的端点表示的一个缺点是它具有太多的自由度，即六个（每个端点三个）而不是 3D 线真正具有的四个自由度。然而，如果我们将线上的两个点固定在特定的平面上，我们就会得到一个具有四个自由度的表示。例如，如果我们表示几乎垂直的线，则 $z = 0$ 和 $z = 1$ 形成两个合适的平面，即两个平面中的 $(x, y)$ 坐标提供了描述线的四个坐标。这种双平面参数化用于描述的光场和基于Lumigraph图像的渲染系统，以表示相机在物体前面移动时看到的光线集合。双端点表示对于表示线段也很有用，即使它们的确切端点无法看到（只能猜测）。

如果我们希望在不偏向任何特定方向的情况下表示所有可能的线，我们可以使用 Plüucker 坐标。这些坐标是 $4\times 4$ 斜对称矩阵中的六个独立非零项

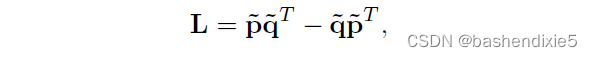
其中 $\tilde{ p }$ 和 $\tilde{ q }$ 是线上的任意两个（不相同的）点。该表示只有四个自由度，因为 L 是齐次的并且还满足 $\left | L \right | = 0$ ，这导致对 Plüucker 坐标的二次约束。

在实践中，最小表示对于大多数应用程序来说不是必需的。可以通过估计它们的方向（可能提前知道，例如，对于建筑）和线的可见部分内的某个点或通过使用两个端点来获得 3D 线的适当模型，因为线通常作为有限线段可见。但是，如果您对有关最小线参数化主题的更多细节感兴趣，Förstner (2005) 讨论了在投影几何中推断和建模 3D 线的各种方法，以及如何估计此类拟合模型中的不确定性。

（7）3D quadrics

圆锥截面的 3D 模拟是二次曲面

同样，二次曲面在多视图几何研究中很有用，也可以用作有用的建模基元（球体、椭球体、圆柱体）。

计算机视觉图像形成几何图形和变换

一、图像形成概述

二、几何图元和变换

1、几何图元

（1）2D points

（2）2D lines

（3）2D conics

（4）3D points

（5）3D planes

（6）3D lines

（7）3D quadrics

猜你喜欢

计算机视觉 图像形成 几何图形和变换

一、图像形成概述

二、几何图元和变换

1、几何图元

（1）2D points

（2）2D lines

（3）2D conics

（4）3D points

（5）3D planes

（6）3D lines

（7）3D quadrics

猜你喜欢

计算机视觉图像形成几何图形和变换